Als PDF, PPTX herunterladen
![Pfadplanung
Konfigurationsraum
Reduzieren einer Pose auf einen Punkt im Konfigurationsraum
Freier Konfigurationsraum:
Cfree = C
i∈{1,...,n}
{q ∈ C | A(q) ∩ Bi = ∅}
Freier Pfad τ : [0, 1] → Cfree, τ(0) = q1, τ(1) = q2
Johannes Diemke Bachelorarbeit 4. September 2012 5/17](https://image.slidesharecdn.com/ba-diemke-prsentation-130629202032-phpapp01/85/Pfadplanung-mit-harmonischen-Potentialfeldern-5-320.jpg)
Hochgeladen vonJohannes Diemke
Pfadplanung mit harmonischen Potentialfeldern
Die Bachelorarbeit von Johannes Diemke behandelt die Verbesserung der Pfadplanung mit harmonischen Potentialfeldern für die Navigation in 2D-Simulationen. Es werden Anforderungen an die neue Methode erörtert, die auf Harmonie und Robustheit abzielen, sowie die Implementierung und Bewertung eines Prototyps, der Echtzeitfähigkeit bietet. Der Entwurf zielt darauf ab, Probleme wie lokale Minima und Oszillationen zu vermeiden und nutzt Technologien wie GPU-Berechnung zur Leistungssteigerung.
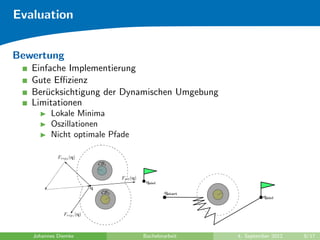
Pfadplanung mit harmonischen Potentialfeldern
- 1. C A RL V O N O S S I E T Z K Y Pfadplanung mit harmonischen Potentialfeldern Johannes Diemke Pr¨asentation zur Bachelorarbeit Sommersemester 2012
- 2. Gliederung 1 Problemstellung 2 Grundlagen 3Anforderungserhebung 4 Evaluation 5 Entwurf und Implementierung 6 Fazit Johannes Diemke Bachelorarbeit 4. September 2012 2/17
- 3. Problemstellung Motivation Pfadplanung mit Potentialfeldernin TORF Nicht vollends zufriedenstellende Ergebnisse Sichere Navigation ist aber wichtige Kompetenz Problemstellung Verbesserung des bestehenden Pfadplaners Johannes Diemke Bachelorarbeit 4. September 2012 3/17
- 4. Pfadplanung Motivation Navigation eines Spielerszu einer Zielposition Positionsverbesserung vor einem Torschuss Anforderungen Vermeiden von Kollisionen Kurzer vs. sicherer Pfad Johannes Diemke Bachelorarbeit 4. September 2012 4/17
- 5. Pfadplanung Konfigurationsraum Reduzieren einer Poseauf einen Punkt im Konfigurationsraum Freier Konfigurationsraum: Cfree = C i∈{1,...,n} {q ∈ C | A(q) ∩ Bi = ∅} Freier Pfad τ : [0, 1] → Cfree, τ(0) = q1, τ(1) = q2 Johannes Diemke Bachelorarbeit 4. September 2012 5/17
- 6. Anforderungserhebung Anforderungen Vollst¨andigkeit Echtzeitf¨ahigkeit Robustheit bzgl. Ungenauigkeiten Ber¨ucksichtigungder dynamischen Umgebung Glatte und sichere Pfade Johannes Diemke Bachelorarbeit 4. September 2012 6/17
- 7. Evaluation Istzustand der Pfadplanung VerwendetPotentialfeldmethode Potentialfeld induziert gerichtete Kraft F = − U Potentialfeld als Superposition U = Uatt + n i=1 Urepi Johannes Diemke Bachelorarbeit 4. September 2012 7/17
- 8. Evaluation Bewertung Einfache Implementierung Gute Effizienz Ber¨ucksichtigungder Dynamischen Umgebung Limitationen Lokale Minima Oszillationen Nicht optimale Pfade Johannes Diemke Bachelorarbeit 4. September 2012 8/17
- 9. Entwurf Harmonische Funktionen L¨osungen derLaplace-Gleichung: 2φ = n i=1 ∂2φ ∂x2 i = 0 Pfadplanung mit harmonischen Funktionen Als Dirichlet-Randwertproblem: 2φ = 0, φ|∂ΩCB = 1, φ|∂ΩZiel = 0 Numerische L¨osung mit Finite-Differenzen-Methode Johannes Diemke Bachelorarbeit 4. September 2012 9/17
- 10. Entwurf Entwurf des neuenPfadplanungsverfahrens Basiert auf harmonischen Funktionen Abgestimmt auf Anforderungen der 2D-Simulationsliga Implizite Repräsentation des Konfigurationsraums durch Distanzfunktionen Diskretisierung des Konfigurationsraums durch ein regelmäßiges Gitter Lösung der Laplace-Gleichung durch ein Splitting-Verfahren Numerische Differentiation und Navigation Johannes Diemke Bachelorarbeit 4. September 2012 10/17
- 11. Entwurf Repr¨asentation des Konfigurationsraums ImpliziteRepr¨asentation durch SDF CB = {p ∈ R2 |DCB(p) ≤ 0} Diskretisierung des Konfigurationsraums Approximation durch regelm¨aßiges Gitter PCfree (p) : DCB(p) − 1 2 ∆x2 + ∆y2 > 0 Johannes Diemke Bachelorarbeit 4. September 2012 11/17
- 12. Implementierung Architektur Auslagerung performancekritischer Teilschritteauf GPU Geschwindigkeitszuwachs durch parallele Berechnung Verwendung von Shader-Programmen Numerische Differentiation und Navigation Diskretisierung des Konfigurationsraums durch ein regelmäßiges Gitter Lösung der Laplace-Gleichung durch das Jacobi-Verfahren Berechnung auf GPUImplizite Repräsentation des Konfigurationsraums durch Distanzfunktionen Berechnung in Client-Anwendung Johannes Diemke Bachelorarbeit 4. September 2012 12/17
- 13. Implementierung Repr¨asentation der Gitterknoten 32-Bit-Floating-Point-Texturen Gitterknotenφi,j entspricht Texel in 2D-Textur GL_RGBA32F 32 bit 32 bit 32 bit 32 bit double-single.high double-single.low boundary-flag Implementierung des Jacobi-Verfahrens Render-Target Ping-Pong-Technik Textur A Textur B Jacobi-Iteration Jacobi-Iteration Johannes Diemke Bachelorarbeit 4. September 2012 13/17
- 14. Implementierung Prototyp Verwendet Java undJOGL 2.0 Intel Core 2 Quad (2,83 GHz) mit GeForce GTX 260 Gitter: 70×40 Iterationen: 2000 Diskretisierung: 39, 06 · 10−4 ms Laplace-Gleichung: 39, 81 ms Bewertung Vermeidet Probleme des alten Pfadplaners Trotz geringer Gitteraufl¨osung glatte Pfade Hardware in Wettk¨ampfen aktuell nicht verf¨ugbar Johannes Diemke Bachelorarbeit 4. September 2012 14/17
- 15. Implementierung Video (Quelle: http://youtu.be/mB6X2p3XROs) Johannes DiemkeBachelorarbeit 4. September 2012 15/17
- 16. Fazit Zusammenfassung Pfadplanung nicht vollendszufriedenstellend Lokale Minima Oszillationen Entwurf eines neuen Pfadplaners Entwicklung eines Prototyps Echtzeitf¨ahige Implementierung m¨oglich Ausblick Zuk¨unftige Verf¨ugbarkeit von 3D-Beschleunigern zu erwarten Einsatz von OpenCL Verwendung von Multigrid Verfahren Integration in TORF Johannes Diemke Bachelorarbeit 4. September 2012 16/17
- 17. Fragen? Vielen Dank f¨urIhre Aufmerksamkeit Johannes Diemke Bachelorarbeit 4. September 2012 17/17