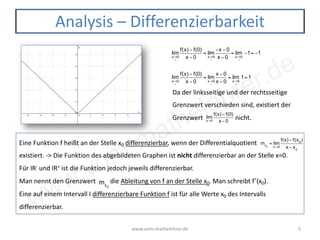
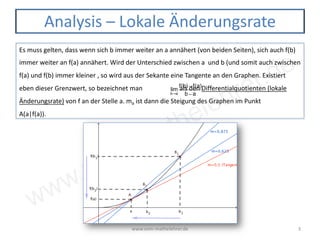
Das Dokument behandelt die Konzepte der mittleren und lokalen Änderungsrate in der Mathematik, einschließlich der Berechnung des Differenzenquotienten und des Differentialquotienten. Es erläutert, wie die mittlere Änderungsrate über ein Intervall und die lokale Änderungsrate an einem bestimmten Punkt bestimmt werden können. Zudem wird die Differenzierbarkeit einer Funktion angesprochen, wobei die Existenz des Differentialquotienten an einem Punkt entscheidend ist.

1. www.vom-mathelehrer.de
Analysis
Änderungsraten
www.vom-mathelehrer.de 1

2. www.vom-mathelehrer.de
www.vom-mathelehrer.de 2
Analysis – Mittlere Änderungsrate
Ist die Funktion f indem Intervall [a; b] definiert, so heißt der Differenzenquotient (die
mittlere Änderungsrate/durchschnittliche Änderung) von f im Intervall [a; b] (Quotient zweier
Differenzen: Differenzenquotient).
(Steigungsdreieck einer Geraden) entspricht der
Steigung der Sekanten durch die Punkte A(a|f(a)) und B(b|f(b)).
f(b) − f(a)
b − a
m =
f(b) − f(a)
b − a
=
Δy
Δx
=
"Höhenunterschied"
"waagrechter Unterschied"

3. www.vom-mathelehrer.de
www.vom-mathelehrer.de 3
Analysis – Lokale Änderungsrate
Es muss gelten, dass wenn sich b immer weiter an a annähert (von beiden Seiten), sich auch f(b)
immer weiter an f(a) annähert. Wird der Unterschied zwischen a und b (und somit auch zwischen
f(a) und f(b) immer kleiner , so wird aus der Sekante eine Tangente an den Graphen. Existiert
eben dieser Grenzwert, so bezeichnet man als den Differentialquotienten (lokale
Änderungsrate) von f an der Stelle a. ma ist dann die Steigung des Graphen im Punkt
A(a|f(a)).
lim
b→a
f(b) − f(a)
b − a

4. www.vom-mathelehrer.de
www.vom-mathelehrer.de 4
Analysis –Änderungsrate Bsp.
Bestimmen Sie für f: f(x)=2x2:
• Die mittlere Änderungsrate im Intervall I=[2; 4],
• die lokale Änderungsrate f‘(2) an der Stelle x0=2.
m =
f(b) − f(a)
b − a
=
f(4) − f(2)
4 − 2
=
2⋅ 42
− 2⋅ 22
4 − 2
=
32−8
2
=12
f '(x0
) = lim
x→x0
f(x) − f(x0
)
x − x0
= lim
x→2
f(x) − f(2)
x − 2
= lim
x→2
2x2
− 2⋅ 22
x − 2
=
= lim
x→2
2(x2
− 4)
x − 2
= lim
x→2
2(x + 2)(x − 2)
x − 2
= lim
x→2
2(x + 2) = 2⋅(2+ 2) = 8

5. www.vom-mathelehrer.de
www.vom-mathelehrer.de 5
Analysis – Differenzierbarkeit
lim
x→0
<
f(x) − f(0)
x −0
= lim
x→0
<
−x −0
x −0
= lim
x→0
<
−1= −1
lim
x→0
>
f(x) − f(0)
x −0
= lim
x→0
>
x −0
x −0
= lim
x→0
>
1=1
Da der linksseitige und der rechtsseitige
Grenzwert verschieden sind, existiert der
Grenzwert nicht.lim
x→0
f(x) − f(0)
x −0
Eine Funktion f heißt an der Stelle x0 differenzierbar, wenn der Differentialquotient
existiert. -> Die Funktion des abgebildeten Graphen ist nicht differenzierbar an der Stelle x=0.
Für IR- und IR+ ist die Funktion jedoch jeweils differenzierbar.
Man nennt den Grenzwert die Ableitung von f an der Stelle x0. Man schreibt f’(x0).
Eine auf einem Intervall I differenzierbare Funktion f ist für alle Werte x0 des Intervalls
differenzierbar.
mx0
= lim
x→0
f(x) − f(x0
)
x − xo
mx0