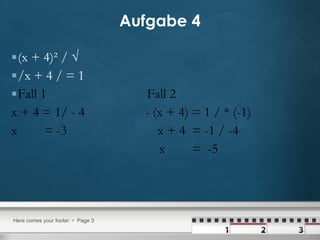
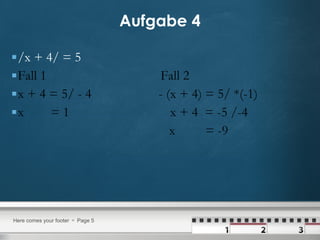
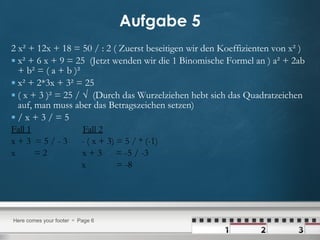
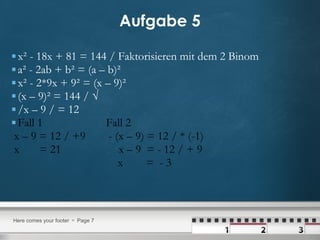
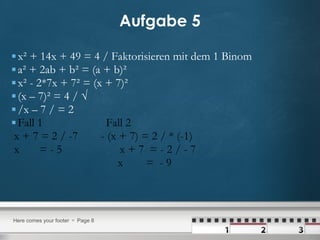
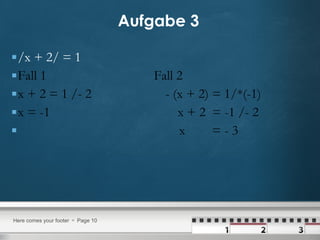
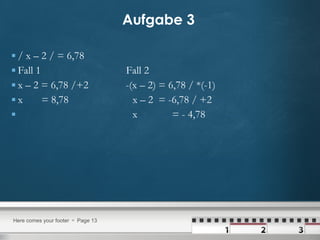
Das Dokument enthält Lösungen zu verschiedenen Aufgaben über quadratische Gleichungen, inklusive der Anwendung der quadratischen Ergänzung und der Binomformel. Es werden mehrere Aufgabenstellungen präsentiert, die jeweils Schritt für Schritt gelöst werden, um die Nullstellen der Gleichungen zu finden. Die Methoden wie die pq-Formel und das Faktorisieren werden ebenfalls mit Beispielen erklärt.

1. Lösungen für die Klassenarbeit über Quadratische Gleichungen

2. Aufgabe 4 2 x² + 16x + 30 = 0 / : 2 x² + 8x + 15 = 0 / - 15 x² + 8x = -15 / Quadratische Ergänzung (8/2)² x² + 8x + 16 = 1 / Jetzt wenden wir die 1. Binomform an a² + 2ab + b² = (a + b )² x² + 2*4x + 4² (x + 4)² / √ Weiter geht es auf der nächsten Seite

3. Aufgabe 4 (x + 4)² / √ /x + 4 / = 1 Fall 1 Fall 2 x + 4 = 1/ - 4 - (x + 4) = 1 / * (-1) x = -3 x + 4 = -1 / -4 x = -5

4. Aufgabe 4 x² + 8x = 9 / Quadratische Ergänzung (8/2)² x² + 8x + 16 = 25 /(Verwendung der 1 Binomformel) a² + 2ab + b² = (a + b )² x² + 2*4x + 4² = 25 (x + 4)² = 25 / √ /x + 4/ = 5 Auf der nächsten Seite geht’s weiter

5. Aufgabe 4 /x + 4/ = 5 Fall 1 Fall 2 x + 4 = 5/ - 4 - (x + 4) = 5/ *(-1) x = 1 x + 4 = -5 /-4 x = -9

6. Aufgabe 5 2 x² + 12x + 18 = 50 / : 2 ( Zuerst beseitigen wir den Koeffizienten von x² ) x² + 6 x + 9 = 25 (Jetzt wenden wir die 1 Binomische Formel an ) a² + 2ab + b² = ( a + b )² x² + 2*3x + 3² = 25 ( x + 3 )² = 25 / √ (Durch das Wurzelziehen hebt sich das Quadratzeichen auf, man muss aber das Betragszeichen setzen) / x + 3 / = 5 Fall 1 Fall 2 x + 3 = 5 / - 3 - ( x + 3) = 5 / * (-1) x = 2 x + 3 = -5 / -3 x = -8

7. Aufgabe 5 x² - 18x + 81 = 144 / Faktorisieren mit dem 2 Binom a² - 2ab + b² = (a – b)² x² - 2*9x + 9² = (x – 9)² (x – 9)² = 144 / √ /x – 9 / = 12 Fall 1 Fall 2 x – 9 = 12 / +9 - (x – 9) = 12 / * (-1) x = 21 x – 9 = - 12 / + 9 x = - 3

8. Aufgabe 5 x² + 14x + 49 = 4 / Faktorisieren mit dem 1 Binom a² + 2ab + b² = (a + b)² x² - 2*7x + 7² = (x + 7)² (x – 7)² = 4 / √ /x – 7 / = 2 Fall 1 Fall 2 x + 7 = 2 / -7 - (x + 7) = 2 / * (-1) x = - 5 x + 7 = - 2 / - 7 x = - 9

9. Aufgabe 3 x² + 4x + 3 = 0 / - 3 x² + 2x = -3 / Quadratische Ergänzung (4/2)² x² + 2x + 4 = 1 / Nun verwendet man die erste Binomformel a²+2ab+b² = (a+b)² x²+2*2x+2² = (x+2)² (x+2)² = 1 / √ /x + 2/ = 1 Weiter geht es auf der nächsten Seite

10. Aufgabe 3 /x + 2/ = 1 Fall 1 Fall 2 x + 2 = 1 /- 2 - (x + 2) = 1/*(-1) x = -1 x + 2 = -1 /- 2 x = - 3

11. Aufgabe 3 x² + 4x - 21 = 0 / + 21 x² + 4x = 21 / Quadratische Ergänzung (4/2)² x² + 4x + 4 = 25 / Die erste Binomformel a²+2ab+b² = (a+b)² x² + 2*2x + 2² = 25 (x+2)²= 25 / √ Fall 1 Fall 2 x+2 = 25 /-2 -(x+2) =25/ *(-1) x = 23 x + 2 = -25 /-2 x = -27

12. Aufgabe 3 x² - 4x - 42 = 0 / + 42 x² - 4x = 42 / Quadratische Ergänzung (4/2)² x² - 4x + 4 = 46 / 2 Binomform a² - 2ab + b² = (a-b)² x² - 2*2x + 2² = 46 (x – 2)² = 46 / √ / x – 2 / = 6,78 Auf der nächsten Seite geht’s weiter

13. Aufgabe 3 / x – 2 / = 6,78 Fall 1 Fall 2 x – 2 = 6,78 /+2 -(x – 2) = 6,78 / *(-1) x = 8,78 x – 2 = -6,78 / +2 x = - 4,78

14. Aufgabe 2 3x² - 3x - 60 = 60 / - 60 (Erst müssen wir es in die Normalform bringen) 3x² - 3x – 120 = 0 /:3 x² - x – 40 = 0 (Jetzt wenden wir die P-Q Formel an P entspricht -1 und Q -40 x1/2 =- -½ + - Wurzel aus (-1/2)² - (-40) x1/2= 0,5 + - 6,34 Fall 1 = 6,84 Fall 2 = -5,84

15. Aufgabe 2 4x² - 12x - 16 = 16 /-16 Wir bringen die Gleichung auf die Normalform 4x² - 12x – 32 = 0 /:4 x² - 3x – 8 = 0 (Anwendung der P-Q-Formel) P entspricht -3 und Q entspricht – 8 x1/2 = - -3/2 + - Wurzel aus (-3/2)² - (-8) x1/2 = 1,5 + - 3,2 Fall 1 = 4.7 Fall 2 = -1,7

16. Aufgabe 2 3x² + 18x + 15 = 15 /-15 (Auf Normalform bringen) 3x² + 18 + 0 = 0 /:3 x² + 6 + 0 = 0 (P-Q Formel anwenden) P entspricht 6 und Q entspricht 0 x1/2 = - 6/2 + - Wurzel aus (6/2)² - 0 x1/2 = - 3 + - 3 Fall 1 = 0 Fall 2 = - 6