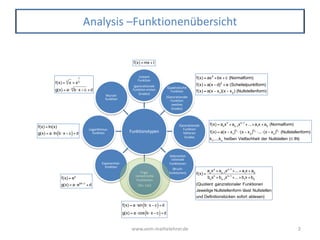
Das Dokument behandelt verschiedene Funktionstypen in der Mathematik, einschließlich linearer, quadratischer und trigonometrischer Funktionen sowie deren Ableitungen und Integrale. Es gibt detaillierte Formeln für jede Funktion, ihre Eigenschaften, wie Nullstellen, Perioden und Transformationsregeln zur Veränderung des Graphen. Außerdem werden die Ableitungs- und Aufleitungsregeln für trigonometrische Funktionen erläutert.

1. www.vom-mathelehrer.de 1

2. Analysis –Funktionenübersicht
Funktionstypen
Lineare
Funktion
(ganzrationale
Funktion ersten
Grades)
Quadratische
Funktion
(Ganzrationale
Funktion
zweiten
Grades)
Ganzrationale
Funktion
höheren
Grades
Gebrochen
rationale
Funktionen
(Bruch-
funktionen)Trigo-
nometrische
Funktionen
(Sin, Cos)
Exponential-
funktion
Logarithmus-
funktion
Wurzel-
funktion
f(x) = mx + t
f(x) = ax2
+bx + c (Normalform)
f(x) = a(x − d)2
+ e (Scheitelpunktform)
f(x) = a(x − x1
)(x − x2
) (Nullstellenform)
f(x) = an
xn
+ an−1
xn−1
+...+ a1
x + a0
(Normalform)
f(x) = a(x − x1
)
k1
⋅(x − x2
)
k2
⋅...⋅(x − xn
)
kn
(Nullstellenform)
k1
,...,kn
heißen Vielfachheit der Nullstellen (∈ IN)
f(x) =
az
xz
+ az−1
xz−1
+...+ a1
x + a0
bn
xn
+bn−1
xn−1
+...+b1
x +b0
(Quotient ganzrationaler Funktionen
Jeweilige Nullstellenform lässt Nullstellen
und Definitionslücken sofort ablesen)
f(x) = a⋅sin b⋅ x − c( )+ d
g(x) = a⋅cos b⋅ x − c( )+ d
f(x) = ex
g(x) = a⋅ebx−c
+ d
f(x) = ln(x)
g(x) = a⋅ln b⋅ x − c( )+ d
f(x) = xn
= x
1
n
g(x) = a⋅ b⋅ x − cn
+ d
www.vom-mathelehrer.de 2

3. www.vom-mathelehrer.de 3
Analysis – Trigonometrische Funktionen
•f(x)=
•D=IR
•W=[-2; +2] -> Amplitude: 4
•Periode P: 2π
•Verschiebung in x-Richtung: +1
•Nullstellen:
Trigonometrische
Funktion
f(x) = sinx
2sin(x −1)
x −1= kπ ⇔ xk
= kπ +1
P =
2π
|b |
⎛
⎝
⎜
⎞
⎠
⎟
x = kπ +
1
2
π
Graphen von trigonometrischen Funktionen:
f(x)=sin(x)
• Df=IR
• Nullstellen: für sin: ; für cos:
• Periodenlänge:
x = kπ
f(x) = sinx

4. www.vom-mathelehrer.de 4
Analysis – Veränderung des Funktionsterms und der Einfluss auf den Graphen
y=-3sin(-3x-3)-3
Streckung/Stauchung y-Richtung
y=-3sin(x)
a=-3: Spiegelung an x-Achse; Streckung
Streckung/Stauchung x-Richtung
y=sin(-3x)
b=-3: Spiegelung an y-Achse; Stauchung
Verschiebung in x-Richtung
y=sin(x-3)
c=3: Verschiebung um 3 Einheiten nach rechts
Verschiebung in y-Richtung
y=sin(x)-3
d=-3: Verschiebung um 3 Einheiten nach unten
y=f(x)
y=sin(x)
a<-1
b<-1 c>0
d<0
y = a⋅ f b⋅ x − c( )+ d

5. www.vom-mathelehrer.de
Analysis – Ableitung Trigonometrische Funktionen
www.vom-mathelehrer.de 5
sin(x) (sin(x))‘
cos(x)
(cos(x))‘
(-sin(x))‘ -sin(x)
-(cos(x))‘
-cos(x)
f(x) = 2sin(3x −1) +0,5
f '(x) = 2sin(3x −1)⋅3
= 6sin(3x −1)
f ''(x) = 6(−sin(3x −1))⋅3
= −18sin(3x −1)
f '''(x) = −18sin(3x −1)⋅3
= −54cos(3x −1)
g(x) = −0,5cos(2x +3)
g'(x) = 0,5sin(2x +3)⋅ 2
= sin(2x +3)
g''(x) = cos(2x +3)⋅ 2
= 2cos(2x +3)
g'''(x) = 2(−sin(2x +3)⋅ 2)
= −4sin(2x +3)

6. www.vom-mathelehrer.de
Analysis – Aufleitung Trigonometrische Funktionen
www.vom-mathelehrer.de 6
sin(x)
cos(x)
-sin(x)
-cos(x)
f(x) = 2sin(3x + 4)
i(x) = 2cos(3x + 4)
G(x) = −
2
3
sin(3x + 4)
F(x) = 2⋅
1
3
⋅(−cos(3x + 4)
= −
2
3
cos(3x + 4)
g(x) = −2cos(3x + 4)
= 2(−cos(3x + 4))
I(x) =
2
3
sin(3x + 4)
H(x) =
2
3
cos(3x + 4)
h(x) = −2sin(3x + 4)

7. www.vom-mathelehrer.de
www.vom-mathelehrer.de 9
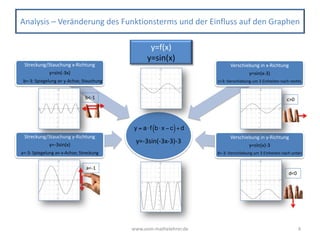
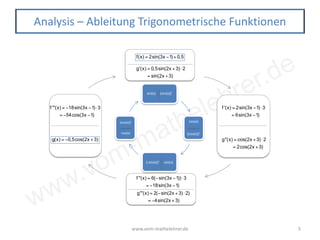
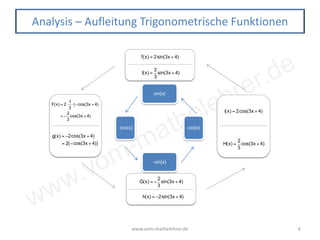
Analysis – Trigonometrische Funktionen
•F(x)=
•Integral:
Stammfunktion
•D=IR
•f(x)=
•W=[-2; +2] -> Amplitude: 4
•Periode P: 2π
•Verschiebung in x-Richtung: +1
•Nullstellen:
Funktion f mit
• f‘=
•f‘(x)=0:
•Extremstellen an den Nullstellen von f‘, da jede mit VZW
1. Ableitung
•f‘‘(x)=
•f‘‘(x)=0:
•Wendepunkte an den Nullstellen von f‘‘, da jede mit VZW
2. Ableitung
•f‘‘‘(x)=
3. Ableitung
Aufleiten
Ableiten
Summenregel
Faktorregel
Produktregel
Quotientenregel
Kettenregel
Verkettete
Funktionen
F(x) = −cosx
f(x) = sinx
f '(x) = cosx
f ''(x) = −sinx
f '''(x) = −cosx
f(x) = 2sin(x −1)
2cos(x −1)
f(x)dx =
1
2π+1
∫ F(2π +1) −F(1) = 0
2sin(x −1)
x −1= kπ ⇔ xk
= kπ +1
−2sin(x −1)
−2cos(x −1)
−2cos(x −1)
P =
2π
|b |
⎛
⎝
⎜
⎞
⎠
⎟
xk
−1= kπ +
1
2
π ⇔ xk
= kπ +
1
2
π +1
x −1= kπ ⇔ xk
= kπ +1