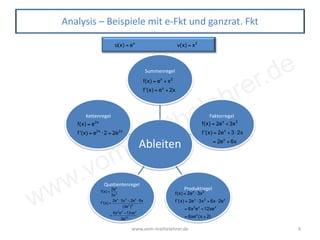
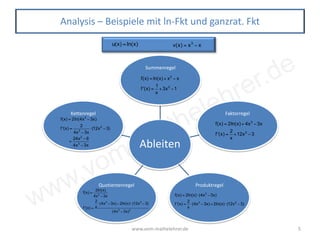
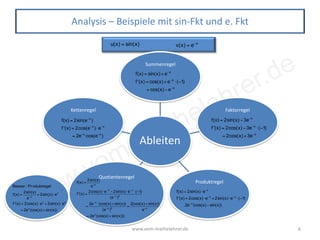
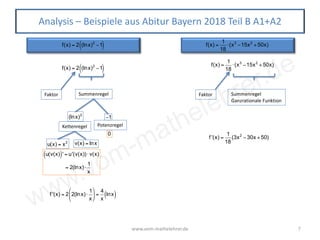
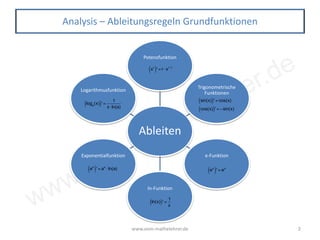
Das Dokument behandelt die Ableitungsregeln in der Mathematik, einschließlich der Grundlagen zum Ableiten von Funktionstypen wie Potenzfunktionen, trigonometrischen Funktionen, Exponential- und Logarithmusfunktionen. Es sind zahlreiche Beispiele zur Anwendung der Summenregel, Faktorregel, Produktregel, Quotientenregel und Kettenregel enthalten. Zusätzlich werden spezifische Ableitungen von Funktionen, die in Abiturprüfungen verwendet werden, besprochen.

1. www.vom-mathelehrer.de
Analysis
Ableitungsregeln
www.vom-mathelehrer.de 1

2. www.vom-mathelehrer.de
www.vom-mathelehrer.de 2
Analysis – Ableitungsregeln Grundfunktionen
Ableiten
Potenzfunktion
Trigonometrische
Funktionen
e-Funktion
ln-Funktion
Exponentialfunktion
Logarithmusfunktion
xr
( )' = r ⋅ xr−1
sin(x)( )' = cos(x)
cos(x)( )' = −sin(x)
ex
( )' = ex
ln(x)( )' =
1
x
ax
( )' = ax
⋅ln(a)
loga
(x)( )' =
1
x ⋅ln(a)

3. www.vom-mathelehrer.de
www.vom-mathelehrer.de 3
Analysis – Ableitungsregeln Übersicht
Ableiten
Summenregel
Faktorregel
ProduktregelQuotientenregel
Kettenregel
f(x) = u(x) + v(x)
f '(x) = u'(x) + v'(x)
f(x) = c ⋅u(x)
f '(x) = c ⋅u'(x)
f(x) = u(x)⋅ v(x)
f '(x) = u'(x)⋅ v(x) + v'(x)⋅u(x)
f(x) =
u(x)
v(x)
f '(x) =
u'(x)⋅ v(x) −u(x)⋅ v'(x)
[v(x)]2
f(x) = u(v(x))
f '(x) = u'(v(x))⋅ v'(x)

4. www.vom-mathelehrer.de
www.vom-mathelehrer.de 4
Analysis – Beispiele mit e-Fkt und ganzrat. Fkt
u(x) = ex
v(x) = x2
Ableiten
Summenregel
Faktorregel
Produktregel
Quotientenregel
Kettenregel
f(x) = ex
+ x2
f '(x) = ex
+ 2x
f(x) = 2ex
+ 3x2
f '(x) = 2ex
+ 3⋅ 2x
= 2ex
+ 6x
f(x) = 2ex
⋅3x2
f '(x) = 2ex
⋅3x2
+ 6x ⋅ 2ex
= 6x2
ex
+12xex
= 6xex
(x + 2)
f(x) =
2ex
3x2
f '(x) =
2ex
⋅3x2
− 2ex
⋅ 6x
(3ex
)2
=
6x2
ex
−12xex
9e2x
f(x) = e2x
f '(x) = e2x
⋅ 2 = 2e2x

5. www.vom-mathelehrer.de
www.vom-mathelehrer.de 5
Analysis – Beispiele mit ln-Fkt und ganzrat. Fkt
u(x) = ln(x) v(x) = x3
− x
Ableiten
Summenregel
Faktorregel
ProduktregelQuotientenregel
Kettenregel
f(x) = ln(x) + x3
− x
f '(x) =
1
x
+ 3x2
−1
f(x) = 2ln(x) + 4x3
− 3x
f '(x) =
2
x
+12x2
− 3
f(x) = 2ln(x)⋅(4x3
− 3x)
f '(x) =
2
x
⋅(4x3
− 3x) + 2ln(x)⋅(12x2
− 3)
f(x) =
2ln(x)
4x3
− 3x
f '(x) =
2
x
⋅(4x3
− 3x) − 2ln(x)⋅(12x2
− 3)
(4x3
− 3x)2
f(x) = 2ln(4x3
− 3x)
f '(x) =
2
4x3
− 3x
⋅(12x2
− 3)
=
24x2
− 6
4x3
− 3x

6. www.vom-mathelehrer.de
www.vom-mathelehrer.de 6
Analysis – Beispiele mit sin-Fkt und e. Fkt
u(x) = sin(x) v(x) = e−x
Ableiten
Summenregel
Faktorregel
Produktregel
Quotientenregel
Kettenregel
f(x) = sin(x) + e−x
f '(x) = cos(x) + e−x
⋅(−1)
= cos(x) − e−x
f(x) = 2sin(x) − 3e−x
f '(x) = 2cos(x) − 3e−x
⋅(−1)
= 2cos(x) + 3e−x
f(x) = 2sin(x)⋅e−x
f '(x) = 2cos(x)⋅e−x
+ 2sin(x)⋅e−x
⋅(−1)
2e−x
(cos(x) − sin(x))
f(x) =
2sin(x)
e−x
f '(x) =
2cos(x)⋅e−x
− 2sin(x)⋅e−x
⋅(−1)
(e−x
)2
=
2e−x
⋅(cos(x) + sin(x))
(e−x
)2
=
2(cos(x) + sin(x))
e−x
= 2ex
(cos(x) + sin(x)))
f(x) = 2sin(e−x
)
f '(x) = 2cos(e−x
)⋅e−x
= 2e−x
cos(e−x
)
Besser : Pr oduktregel
f(x) =
2sin(x)
e−x
= 2sin(x)⋅ex
f '(x) = 2cos(x)⋅ex
+ 2sin(x)⋅ex
= 2ex
(cos(x) + sin(x))

7. www.vom-mathelehrer.de
www.vom-mathelehrer.de 7
Analysis – Beispiele aus Abitur Bayern 2018 Teil B A1+A2
f(x) = 2 (lnx)2
−1( )
f(x) = 2 (lnx)2
−1( )
Faktor Summenregel
(lnx)2
Kettenregel
u(v(x)( )' = u'(v(x))⋅ v(x)
= 2(lnx)⋅
1
x
−1
Potenzregel
0
f '(x) = 2 2(lnx)⋅
1
x
⎛
⎝
⎜
⎞
⎠
⎟ =
4
x
lnx( )
f(x) =
1
18
⋅(x3
−15x2
+50x)
Faktor Summenregel
Ganzrationale Funktion
f '(x) =
1
18
(3x2
−30x +50)
f(x) =
1
18
⋅(x3
−15x2
+50x)
u(x) = x2 v(x) = lnx

8. www.vom-mathelehrer.de
www.vom-mathelehrer.de 8
Analysis – Beispiele aus Abitur Bayern 2017 Teil B A1+A2
f(x) = 3x −1+lnx( )
Produktregel
(Oder Ausmultiplizieren
-> Summenregel mit Produktregel)
u(x) = 3x
Potenzregel
u'(x) = 3
v(x) = −1+lnx
Summenregel +
Ableitung ln
v'(x) =
1
x
f '(x) = u'(x)v(x) + v'(x)u(x)
= 3 −1+lnx( )+
1
x
⋅3x
= −3+3lnx +3 = 3lnx
f(x) = 2e−x
2e−x
−1( )
f '(x) = u'(x)v(x) + v'(x)u(x)
= −2e−x
2e−x
−1( )+(−2e−x
)⋅ 2e−x
= 2e−x
1− 2e−x
( )− 2e−x
⋅ 2e−x
= 2e−x
1− 2e−x
− 2e−x
( )
= 2e−x
1− 4e−x
( )
f(x) = 3x −1+lnx( ) f(x) = 2e−x
2e−x
−1( )
Produktregel
(Oder Ausmultiplizieren
-> Summenregel mit Produktregel)
u(x) = 2e−x
Faktor- und Kettenregel
u'(x) = 2e−x
⋅(−1) = −2e−x
v(x) = 2e−x
−1
Faktor- und Kettenregel
v'(x) = 2e−x
⋅(−1) = −2e−x