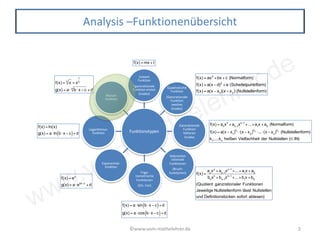
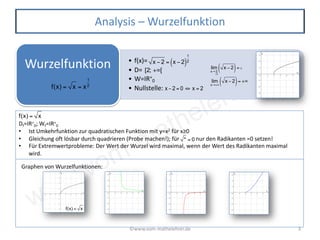
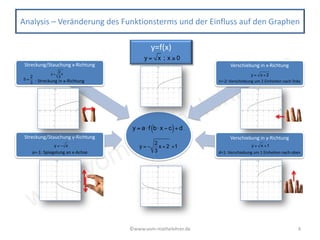
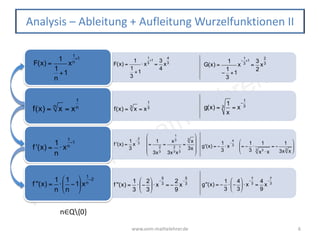
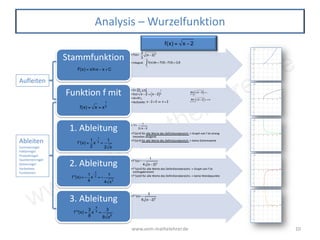
Das Dokument behandelt verschiedene Funktionstypen, insbesondere die Wurzelfunktion, und deren Eigenschaften, einschließlich Ableitungen und Integrale. Es beschreibt die Formeln, die für die Analyse und das Zeichnen von Graphen dieser Funktionen relevant sind, sowie deren Extremwerte und Monotonie. Die Umkehrbeziehung zur quadratischen Funktion wird hervorgehoben, und es werden Informationen zu Transformationen der Funktion gegeben.