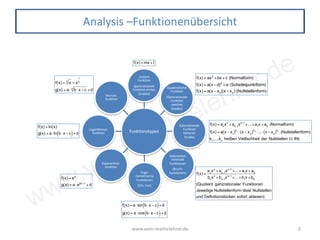
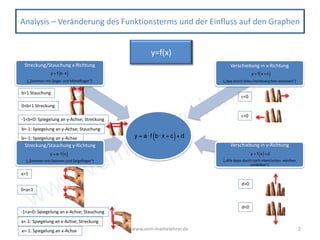
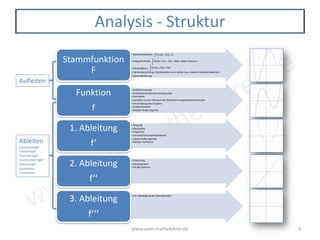
Das Dokument bietet einen umfassenden Überblick über verschiedene Funktionstypen in der Mathematik, darunter ganzrationale, exponentielle, logarithmische und trigonometrische Funktionen sowie deren Eigenschaften und Transformationen. Es behandelt wichtige Konzepte wie das Ableiten, Integrieren, Extremwertaufgaben und die Analyse von Graphen. Zudem werden Methoden zur Flächenberechnung, Symmetrie, Monotonie und die Anwendung des Newtonverfahrens behandelt.