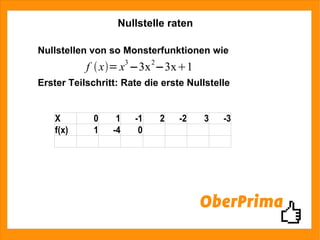
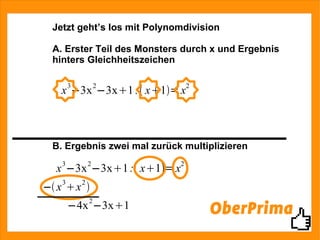
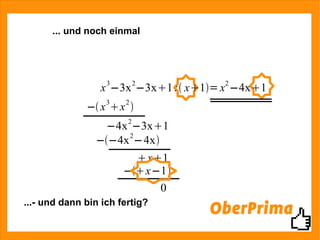
Das Dokument behandelt die Polynomdivision zur Berechnung von Nullstellen komplexer Funktionen. Es erklärt die Schritte zur Bestimmung einer Nullstelle und die Anwendung der pq-Formel zur Berechnung weiterer Nullstellen. Zusätzlich wird auf verfügbare Präsentationen und die Möglichkeit zur Kontaktaufnahme für weitere Fragen hingewiesen.

1. Polynomdivision – oder Wie berechne ich die Nullstellen von Funktionen, die so ähnlich aussehen wie:

2. Was wir kennen, um Nullstellen zu berechnen: Nullstelle von y = x + 5 | - 5

3. Hinweis auf Grundlagen - Präsentation Was wir kennen, um Nullstellen zu berechnen: Nullstelle von Dazu haben wir auf OberPrima.com eine Extra-Präsentation. Wer zur Berechnung von Nullstellen quadratischer Funktionen Fragen hat, sollte sich die mal angesehen haben ;-)

4. Nullstelle raten Nullstellen von so Monsterfunktionen wie Erster Teilschritt: Rate die erste Nullstelle

5. Zweiter teilschritt: Schreibe auf: Monster geteilt durch (x- „die geratene nullstelle“) ist gleich (so wie unten)

6. Jetzt geht’s los mit Polynomdivision A. Erster Teil des Monsters durch x und Ergebnis hinters Gleichheitszeichen B. Ergebnis zwei mal zurück multiplizieren

7. Das ganze machen wir jetzt noch einmal Das ganze machen wir jetzt noch einmal

8. ... und noch einmal ...- und dann bin ich fertig?

9. Mit der Polynomdivision sind wir dann fertig. Das ist aber nur eine Technik. Wir wollen ja die Nullstellen von der Monsterfunktion rauskriegen und dazu müssen, können, dürfen und wollen wir jetzt mit der Technik: „pq-formel“ die restlichen Nullstellen ausrechen. Dazu haben wir eine Extra-Präsentation zur Verfügung gestellt... Wer mehr davon verstehen will, ruft uns an, oder sagt seinen oder ihren Eltern Bescheid, damit die uns anrufen ;)