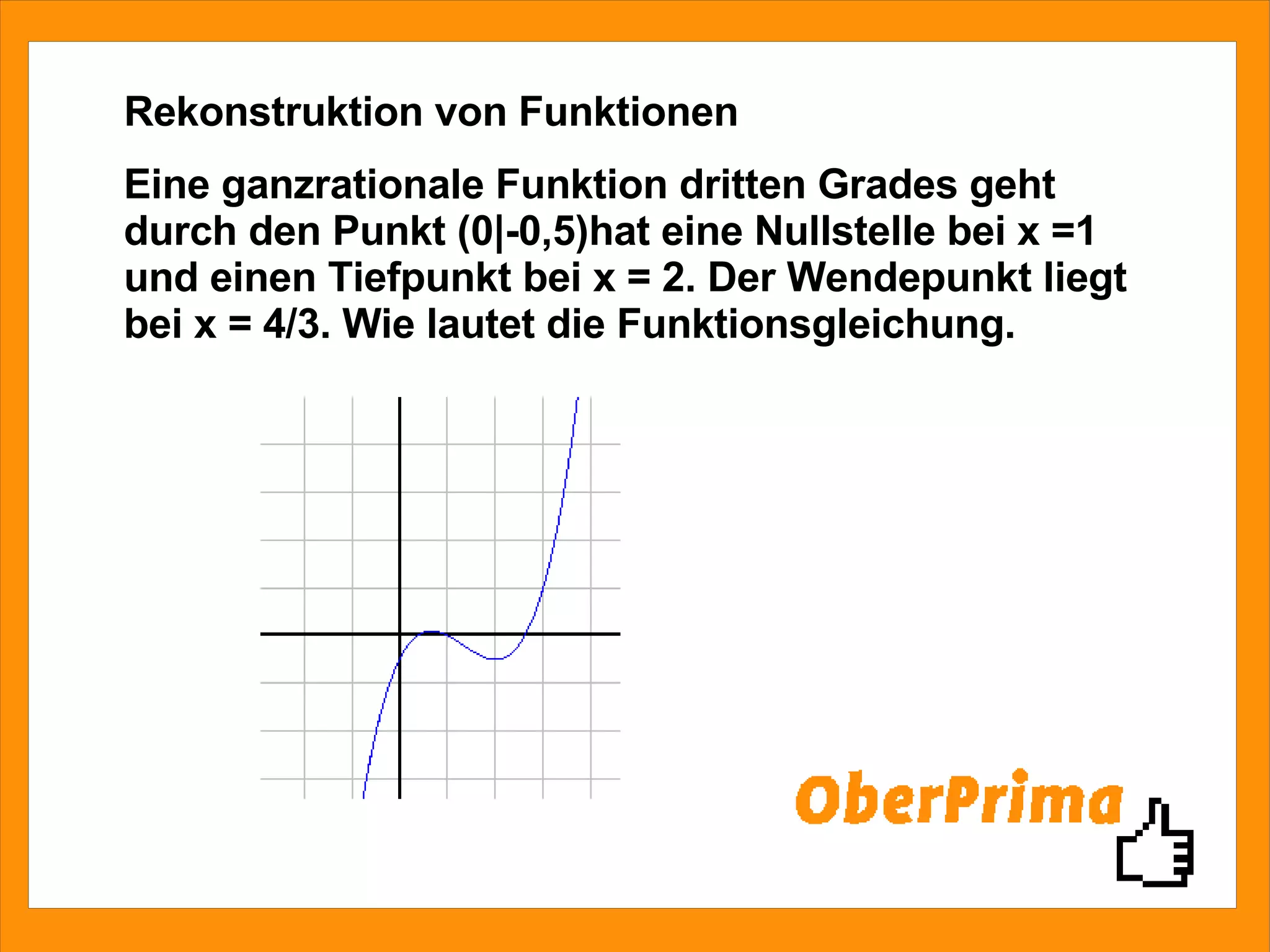
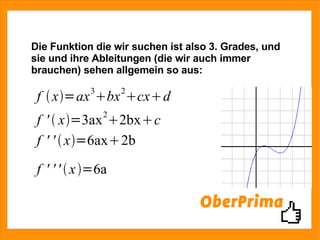
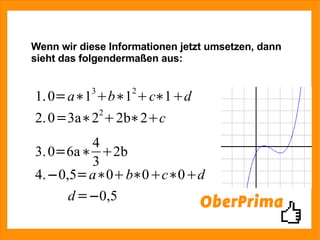
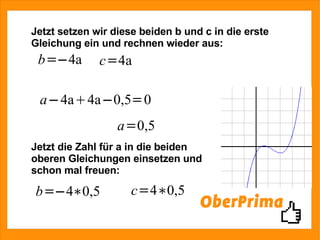
Das Dokument beschreibt die Bestimmung der Funktionsgleichung einer ganzrationalen Funktion dritten Grades, die durch den Punkt (0|-0,5) verläuft, eine Nullstelle bei x=1 hat und bei x=2 einen Tiefpunkt aufweist. Es wird ein Gleichungssystem mit drei Gleichungen und drei Unbekannten aufgestellt und gelöst, um die Koeffizienten der Funktion zu finden. Der Text führt die Schritte zur Rekonstruktion und Lösung des Problems ausführlich auf.

1. Eine ganzrationale Funktion dritten Grades geht durch den Punkt (0|-0,5)hat eine Nullstelle bei x =1 und einen Tiefpunkt bei x = 2. Der Wendepunkt liegt bei x = 4/3. Wie lautet die Funktionsgleichung. Rekonstruktion von Funktionen

2. Die Funktion die wir suchen ist also 3. Grades, und sie und ihre Ableitungen (die wir auch immer brauchen) sehen allgemein so aus:

3. Dann sammeln wir alle Informationen aus dem Aufgabentext und übersetzen diese in Mathesprache:

4. Wenn wir diese Informationen jetzt umsetzen, dann sieht das folgendermaßen aus:

5. Jetzt lösen wir das Gleichungssystem, zunächst aber alles ausrechen, was man ausrechnen kann.Gleichzeitig kann die Erkenntnis aus der 4. Gleichung in 1. eingesetzt werden:

6. Das nennt sich ein Gleichungssystem mit 3 Gleichungen und 3 Unbekannten. Sowas ist lösbar ;). Supersicher mit dem Einsetzungsverfahren, da braucht man fast nicht nachzudenken... Die 3. Gleichung (die einfachste) löse ich nach b auf: Und setze das in die 2. Gleichung ein und stelle nach c um:

7. Jetzt setzen wir diese beiden b und c in die erste Gleichung ein und rechnen wieder aus: Jetzt die Zahl für a in die beiden oberen Gleichungen einsetzen und schon mal freuen:

8. Dann können wir jetzt die Gleichung aufschreiben: Und in der Klausur schreiben wir natürlich alle einen schönen Antwortsatz mit Satzzeichen, wa?