Das Dokument behandelt die EMV-Messtechnik und spezifische Experimente mit einer Platine von Würth Elektronik, die für die Lehre im Bereich Elektrotechnik entwickelt wurde. Es werden verschiedene Aspekte von Tiefsetzstellern untersucht, darunter deren physische und charakteristische Beeinflussung sowie Verlustleistungen bei unterschiedlichen Induktivitäten und Frequenzen. Ziel ist es, das Verständnis für die Schalteinheiten und deren Anwendung in praktischen Experimenten zu fördern, um Studierende zur Wahl eines Elektrotechnik-Studiums zu motivieren.

1. Otto-von-Guericke-Universität Magdeburg
Fakultät für Elektrotechnik und Informationstechnik
Dokumentation
EMV-Messtechnik
TI-PMLK Buck Würth Elektronik Edition
eingereicht am: 21. September 2020
von: Christina Bertram
Vincent Szameitat
Pierre Bolz
Betreuer: Dr.-Ing. Mathias Magdowski

2. Inhaltsverzeichnis
1 Einleitung 1
1.1 Aufgabe und Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2 Grundlagen zum Tiefsetzsteller . . . . . . . . . . . . . . . . . . . . . . . . 1
1.3 Aufbau der Platine TI-PMLK BUCK-WE . . . . . . . . . . . . . . . . . . 3
2 Experimente mit dem Board 5
2.1 Physische und charakteristische Beeinflussung der Induktivität . . . . . . . 6
2.2 Verluste des Tiefsetzstellers bei unterschiedlichen Induktivitäten und Schalt-
frequenzen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.3 Untersuchungen zur Ausgangsfilterfunktion mit verschiedenen Kondensato-
ren eines Tiefsetzstellers . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.4 Untersuchungen zur Eingangsfilterfunktion verschiedener Induktivitäten
eines Tiefsetzstellers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.5 EMV-Störaussendung des Experimentierboards . . . . . . . . . . . . . . . 19
3 Fazit 25
Literaturverzeichnis 27
A Schaltpläne 29
i

3. Abbildungsverzeichnis
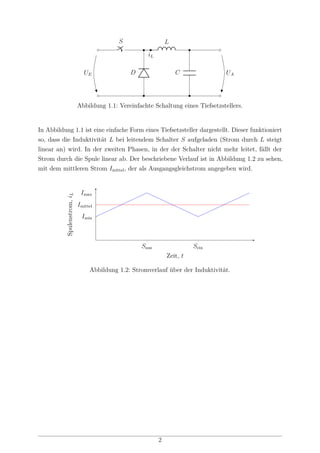
1.1 Vereinfachte Schaltung eines Tiefsetzstellers. . . . . . . . . . . . . . . . . . 2
1.2 Stromverlauf über der Induktivität. . . . . . . . . . . . . . . . . . . . . . . 2
1.3 Platine TI-PMLK BUCK-WE (nach [1]) . . . . . . . . . . . . . . . . . . . 3
2.1 Erweiterte Schaltung des Tiefsetzstellers [1] . . . . . . . . . . . . . . . . . . 5
2.2 Kennzeichnung der in den Versuchen verwendeten Bauelemente (nach [1]) . 6
2.3 Versuchsaufbau des ersten Versuches (nach [1]) . . . . . . . . . . . . . . . . 7
2.4 Schaltzeitpunkt des Leistungshalbleiters (gelb) und resultierender Rippel-
strom (grün) bei einer Schaltfrequrenz von ≈ 300 kHz. . . . . . . . . . . . . 8
2.5 Schaltzeitpunkt des Leistungshalbleiters (gelb) und resultierender Rippel-
strom (grün) bei einer erhöhten Schaltfrequenz von ≈ 450 kHz. . . . . . . . 8
2.6 Versuchsaufbau des zweiten Versuches (nach [1]) . . . . . . . . . . . . . . . 9
2.7 Aufteilung des Tiefsetzstellers [1] . . . . . . . . . . . . . . . . . . . . . . . 12
2.8 Idealer Ausgangsstrom und ideale Ausgangsspannung eines Elektrolytkon-
densators [1] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.9 Idealer Ausgangsstrom und ideale Ausgangsspannung eines Keramikkon-
densators [1] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.10 Zu erwartender Ausgangsstrom und zu erwartende Ausgangsspannung bei
einer realen Messung mittels Oszilloskop [1] . . . . . . . . . . . . . . . . . 15
2.11 Versuchsaufbau des dritten Versuches (nach [1]) . . . . . . . . . . . . . . . 16
2.12 Gemessener Ausgangsstrom und gemessene Ausgangsspannung des Elektro-
lytkondensators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.13 Gemessener Ausgangsstrom und gemessene Ausgangsspannung des Kera-
mikkondensators . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.14 Dämpfungsprinzip: Tiefsetzsteller mit RL-Zweig [1] . . . . . . . . . . . . . 18
2.15 Filterung mit den Spulen L7 und L8 [1] . . . . . . . . . . . . . . . . . . . . 19
2.16 Messung der Störaussendung des Experimentierboards mit Hilfe eines Os-
zilloskops. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.17 Veranschaulichung der galvanischen Kopplung. . . . . . . . . . . . . . . . . 21
2.18 Veranschaulichung der kapazitiven Kopplung. . . . . . . . . . . . . . . . . 22
ii

4. 2.19 Veranschschaulichung der induktiven Kopplung. . . . . . . . . . . . . . . . 23
A.1 In diesem Schaltungsausschnitt sind die Spulen (Induktivitäten) zur Analyse
der physischen und charakteristischen Beeinflussung, gekennzeichnet. [1] . . 29
A.2 In diesem Schaltungsausschnitt sind die Spulen gekennzeichnet, mit denen
die Verluste ermittel werden. [1] . . . . . . . . . . . . . . . . . . . . . . . . 30
A.3 In diesem Schaltungsausschnitt sind die Spulen und die Kondensatoren des
Ausgangsfilters gekennzeichnet. [1] . . . . . . . . . . . . . . . . . . . . . . . 31
A.4 In diesem Schaltungsausschnitt sind die ursprünglichen Spulen und die
Spulen des zusätzlichen Zweiges des Eingangsfilters gekennzeichnet [1] . . . 31
A.5 In diesem Schaltungsausschnitt sind die Jumper gekennzeichnet [1] . . . . . 32
A.6 Darstellung des kompletten Schaltplans der Platine [1] . . . . . . . . . . . 33
iii

5. 1 Einleitung
1.1 Aufgabe und Motivation
Ein Studium der Elektrotechnik muss nicht immer trocken und theoretisch sein. Im Gegen-
teil: Elektrotechnik und Elektronik kann auch viel Spaß machen. Im Rahmen dieser Arbeit
ist eine Reihe von Experimenten an einer Leistungsplatine durchgeführt worden. Die sich
darauf befindende Technologie ist von „Texas Instruments“ und von „Würth Elektronik“
speziell für die Lehre abgewandelt worden. Sie trägt den Namen TI-PMLK BUCK-WE.
Begleitend zur Platine hat Würth Elektronik auf seiner Website ein Experimentierbuch
veröffentlicht [1], in welchem insgesamt sechs Versuche detailliert beschrieben werden.
Dieses dient als Grundlage für das durchgeführte Laborpraktikum. Neben dem Durch-
führen und Dokumentieren einiger ausgewählter Versuche ist insbesondere auch eine
audiovisuelle Begleitung der Platine erfolgt, so dass das Material interessierten Abituri-
ent*innen vorgeführt werden kann und bestenfalls mehr junge Menschen motiviert werden
können, ein Studium im Bereich der Elektrotechnik zu beginnen. Das begleitende Ma-
terial wurde auf einem extra dafür eingerichteten Twitter-Account veröffentlicht (Link:
https://twitter.com/EmvOvgu).
1.2 Grundlagen zum Tiefsetzsteller
Auf der in diesem Dokument beschriebenen Platine befinden sich zwei Tiefsetzsteller, die
zum Beispiel mit Potentiometern, Sicherungen oder Induktivitäten ergänzt wurden. In
diesem Abschnitt soll es lediglich um die Grundlagen eines Tiefsetzstellers gehen, auf den
Aufbau der eigentlichen Platine wird in Abschnitt 1.3 näher eingegangen.
Ein Tiefsetzsteller dient im Allgemeinen dazu aus einer Gleichspannung am Eingang
eine niedrigere Gleichspannung am Ausgang bereitzustellen. Dies wird zum Beispiel bei
Netzteilen angewendet, die auch für das Laden von Smartphones genutzt werden. In diesem
Fall muss die sinusförmige Netzspannung zuerst gleichgerichtet werden. Anschließend kann
die Amplitude von 230 V auf 5 V herabgesetzt werden.
1

6. S L
iL
D CUE UA
Abbildung 1.1: Vereinfachte Schaltung eines Tiefsetzstellers.
In Abbildung 1.1 ist eine einfache Form eines Tiefsetzsteller dargestellt. Dieser funktioniert
so, dass die Induktivität L bei leitendem Schalter S aufgeladen (Strom durch L steigt
linear an) wird. In der zweiten Phasen, in der der Schalter nicht mehr leitet, fällt der
Strom durch die Spule linear ab. Der beschriebene Verlauf ist in Abbildung 1.2 zu sehen,
mit dem mittleren Strom Imittel, der als Ausgangsgleichstrom angegeben wird.
Saus Sein
Imin
Imittel
Imax
Zeit, t
Spulenstrom,iL
Abbildung 1.2: Stromverlauf über der Induktivität.
2

7. 1.3 Aufbau der Platine TI-PMLK BUCK-WE
Elektromagentisches
Interferenzfilter
LEDs zum Anzeigen
des Platinenstatus
Eingänge für
Banenenstecker
Drehsteller zum
Einstellen der
Schaltfrequenz
Testpunkte für
verschiedene
Messungen
Individuell auswähl-
bare Spulen
Rauscharme Testpunkte
LM3475TPS54160
Transformatoren für
die Strommessung
Auswahl zwischen DC-
und AC-Anteil des
Ausgangsstroms
Abbildung 1.3: Platine TI-PMLK BUCK-WE (nach [1])
Die Platine TI-PMLK BUCK-WE wurde von Würth Elektronik speziell für die Lehre
entwickelt. Sie soll Studierenden die Möglichkeit geben theoretische Kenntnisse der Schal-
tungstechnik praktisch zu validieren und zu erweitern. Im Speziellen geht es bei dieser
Platine darum den Einfluss verschiedener Spulen auf die DC-DC-Wandlung, genauer auf
das Herabsetzen einer Gleichspannung, ersichtlich zu machen.
Die Platine ist in Bild 1.3 erstmalig dargestellt. Mit den beigefügten Beschriftungen
(übersetzt und ergänzt nach [1]) kann sich bereits ein Bild vom Aufbau gemacht werden.
Wie leicht zu erkennen ist, teilt sich die Platine in drei große Einheiten auf. So besteht sie
aus einem unteren (grün eingerahmt) und oberen Tiefsetzsteller (blau eingerahmt) sowie
der Spannungsversorgung im mittleren Teil. Der entsprechende Schaltplan ist in Anhang
A.6 dargestellt.
Beide Tiefsetzsteller benutzen Regler von Texas Instruments (Modell LM3475 oben, bzw.
Modell TPS54160 unten). Die Tiefsetzsteller unterscheiden sich neben den Eingangsspan-
nungen (näheres s. Tabelle 1.1) vor allem im Prinzip der Regelung.
Während der TPS54160 eine klassische Maximalstromregelung (engl. peak-current controll)
mit Pulsweitenmodulation verwendet, wird im LM3475 eine Hysterese-Regelung genutzt.
Diese Alternative für niedrige Spannungen steuert den Schalter statt der herkömmlichen
Pulsweitenmodulation mit einer Pulsfrequenzmodulation an und soll laut Hersteller für
eine höhere Regelgenauigkeit und ein sehr schnelles Einschwingen sorgen [2].
3

8. Tabelle 1.1: Übersicht der beiden Tiefsetzsteller
LM3475 TPS54160
Regelprinzip hysteresisch Maximalstrom
Eingangsspannung 5 bis 10 V 6 bis 18 V
Maximale Ausgangsspannung 3,3 V 3,3 V
Maximaler Laststrom 1,2 A 1,2 A
Die Spannungsversorgung erfolgt über das Anschließen von Bananensteckern im Mittelteil.
Direkt neben den Eingängen liegen drei Anschlüsse. Durch Verbinden des mittleren mit dem
oberen bzw. unteren Anschluss kann entschieden werden, welcher der beiden Tiefsetzsteller
in Betrieb genommen werden soll.
Es ist möglich die Schaltfrequenz über einen Drehsteller einzustellen bzw. auch fließend zu
verändern.
Weiterhin stehen elektromagnetische Interferenzfilter zur Verfügung, die Netzstörungen
unterdrücken sollen. Es besteht die Möglichkeit diese zu überbrücken, um Vergleiche
zwischen gefilterter und ungefilterter Netzspeisung zu ziehen.
Für beide Tiefsetzsteller stehen jeweils drei unterschiedliche Spulen zur Verfügung, so
dass mit Hilfe der Versuche Rückschlüsse auf den Einfluss von Kernmaterial, Größe oder
Induktivität beim Tiefsetzstellen gezogen werden können.
Zum Auswerten der Ergebnisse stehen eine Vielzahl von verschiedenen Messpunkten zur
Verfügung, darunter auch Messpunkte mit extra reduziertem Rauschen.
Durch Strommesstransformatoren (engl. current sense transformators) werden Ströme in
formgleiche Spannungen umgewandelt, so dass z.B. Spulenströme auch direkt am Ausgang
mit dem Oszilloskop gemessen werden können. Durch Verbinden zweier weiterer Ports
kann gewählt werden, ob der DC- oder AC-Anteil des Stromes ausgegeben werden soll.
4

9. 2 Experimente mit dem Board
Wie in der Einleitung bereits beschrieben, basieren alle Versuche auf den Grundlagen
des Tiefsetzstellers. Dabei ist die vereinfachte Schaltung um mehrere Bauelemente wie in
Abbildung 2.1 dargestellt, ergänzt wurden.
Abbildung 2.1: Erweiterte Schaltung des Tiefsetzstellers [1]
Bei den Versuchen handelt es sich um sechs unabhängige Experimente bei denen jeweils
ein andere Teil der Platine im Gebrauch ist. Im Rahmen dieser Arbeit wurden 4 Versuche
der Anleitung, die gewissermaßen auch für Schülerpraktikant*innen in Frage kommen
könnten, behandelt. Dabei sind der charakteristische Aufbau der Bauelemente (Kap. 2.1),
die Verluste des Tiefsetzstellers unter Nutzung verschiedener Spulen (Kap. 2.2) und die
Eingangs - und Ausgangsfilterfunktionen (Kap. 2.3 und Kap. 2.4) untersucht worden.
Außerdem wurde unabhängig von der Anleitung die EMV-Störabstrahlung (Kap. 2.5)
betrachtet. Die entsprechenden Bauelemente zum jeweiligen Versuch sind in Abbildung
2.2 bzw. in den Schaltplänen im Anhang A.1 bis Anhang A.4 gekennzeichnet.
5

10. L4, L5, L6
L1, L2, L3
Ausgangsfilter
La =L4, L5, L6
+
Ca=Kerko/Elko
Elektrolyt-
kondensator
Keramik-
kondensator
Cin = Σ (C8...C13)
Lf (Ld)= L7 (L8)
Lf (Ld)= L9 (L10)
Cin = Σ (C29...C34)
unterer
Eingangsfilter
oberer
Eingangsfilter
Abbildung 2.2: Kennzeichnung der in den Versuchen verwendeten Bauelemente (nach [1])
2.1 Physische und charakteristische Beeinflussung der
Induktivität
Das Ziel dieses Versuches ist es, die Induktivität verschiedener Spulen (L1, L2, L3) in
Abhängigkeit von deren physikalischen Eigenschaften und Betriebsbedingungen in einer
DC-Schaltregleranwendung, zu untersuchen. Dabei wird zwischen Spulen mit Ferritkern
und Spulen mit Pulverkern unterschieden. Diese sind in Abbildung 2.2 und im Schaltpla-
nausschnitt im Anhang A.1 gekennzeichnet. Prinzipiell bestehen Magnetkerne aus einem
weichmagnetischen Werkstoff mit möglichst hoher magnetischer Sättigungsflussdichte und
hoher magnetischer Permeabilität. Dadurch wird der magnetische Fluss, der bei Stromfluss
durch den elektrischen Leiter der Spule entsteht, verlustarm gebündelt und die Induktivität
erhöht. Eine hohe Permeabilität erhöht das Magnetfeld einer Induktivität um bis zu fünf
Zehnerpotenzen gegenüber einer Induktivität mit Luft als Kern, wodurch die Abmessungen
der Induktivität mit einem Magnetkern kleiner als bei einer Luftspule werden können. Als
Werkstoffe für Magnetkerne werden entweder ferromagnetische Metalllegierungen, meist
in Form von Blech bzw. Folie (Elektroblech, Metallisches Glas) oder gebundenem Pulver
(Pulverkern) eingesetzt. Es ist auch eine Nutzung von oxidkeramischen, ferromagnetischen
Werkstoffen (Ferrite/Ferritkerne) möglich. Entscheidend für die Anwendung von Werkstof-
fen für Magnetkerne sind die bei Wechselstrom auftretenden Verluste [3]. Diese, das heißt
Eisen- bzw. Kernverluste sowie weitere Verluste, die in einem Tiefsetzsteller auftreten
6

11. können, sind Bestandteil des zweiten Versuches (Kap. 2.2). Dieser Versuch beschränkt
sich auf die Ermittlung der Induktivität mittels Schaltung aus Abbildung (2.1) und dem
Versuchsaufbau, welcher in Abbildung 2.3 dargestellt ist.
CH1 CH2
+
Abbildung 2.3: Versuchsaufbau des ersten Versuches (nach [1])
L = [UD1 + RL · IA + UA] ·
1 − D
fsw · ∆iLPP
(2.1)
wobei:
UD1 Diodenspannung
RL Lastwiderstand
IA Ausgangsstrom
UA Ausgangsspannung
D Tastgrad
fsw Schaltfrequenz
∆iLpp Spitzenlaststrom
Die eigentliche Aufgabe dieses Versuches besteht darin, die genannten Parameter zu messen
und daraus die drei Induktivitäten mittels Formel (2.1) zu ermitteln. Nach Lehrbuch ist
ein Vier-Kanal-Oszilloskop zu nutzen. Dabei sollen u.a. gleichzeitig die Eingangsspannung,
der Tastgrad, die Amplitude des Spitze-Spitze-Stroms durch die jeweilige Spule und
7

12. die Ausgangsspannung gemessen werden. Im Rahmen dieser Arbeit stand lediglich ein
Oszilloskop mit zwei Kanälen zur Verfügung. Aus diesem Grund wurden nur der Spitze-
Spitze-Spulenstrom, sowie die Spannung über dem Leistungshalbleiter gemessen.
Abbildung 2.4: Schaltzeitpunkt des Leistungshalbleiters (gelb) und resultierender Rippel-
strom (grün) bei einer Schaltfrequrenz von ≈ 300 kHz.
Abbildung 2.5: Schaltzeitpunkt des Leistungshalbleiters (gelb) und resultierender Rippel-
strom (grün) bei einer erhöhten Schaltfrequenz von ≈ 450 kHz.
Die Amplitude des Spitze-Spitze-Stroms, der durch die jeweilige Spule fließt, wird durch
einige Parameter beeinflusst. Bei gegebener Ausgangsspannung handelt es sich bei den
8

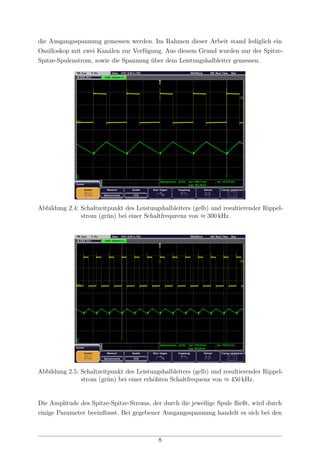
13. wesentlichen Parametern um die Induktivität L, die Eingangsspannung Ue und die Schalt-
frequenz fsw. In den Abbildungen 2.4 und 2.5 ist der Spitze-Spitze-Strom, der durch die
Spulen fließt und die Eingangsspannung dargestellt. Es ist erkennbar, dass mit einer Erhö-
hung der Schaltfrequenz die Welligkeit sowie der Spitzenwert des Stroms abnimmt, wobei
der Strommittelwert gleich bleibt. Die Welligkeit nimmt also zu, wenn die Induktivität
und Schaltfrequenz sich verringert sowie bei Erhöhung der Eingangsspannung. Ein-und
Ausgangsspannung bestimmen ebenfalls den Wert des Tastgrades D. Dieser wie auch die
Induktivität ist nicht ermittelt worden, da für Schülerpraktikant*innen die mathematische
Ermittlung eher uninteressant wäre. In diesem wie auch in den folgenen Versuchen ist
mehr Wert auf die Praxis gelegt worden.
2.2 Verluste des Tiefsetzstellers bei unterschiedlichen
Induktivitäten und Schaltfrequenzen
Der zweite im Experimentierbuch vorgestellte Versuch befasst sich mit den am Tief-
setzsteller auftretenden Verlusten. Diese sollen insbesondere im Zusammenhang mit der
verwendeten Spule stehen. Für beide Tiefsetzsteller stehen je drei Spulen zur Verfügung,
die es zu testen galt. Diese sind in Abbildung 2.2 sowie im Schaltplan (A.2) gekennzeichnet.
In 2.6 ist der Versuchsaufbau dargestellt.
A
A
V
V
+
Abbildung 2.6: Versuchsaufbau des zweiten Versuches (nach [1])
Als weiterer Einflussfaktor der Verluste soll die Schaltfrequenz betrachtet werden. Diese
9

14. kann über einen Drehschalter eingestellt werden.
Es ist zu beachten, dass sich die Gesamtverluste aus verschiedenen Teilverlusten zusammen-
setzen. Grob betrachtet gliedern diese sich in ohmsche, magnetische und Schaltverluste [4].
Die ohmschen Verluste treten in allen passiven Bauelementen sowie den Verbindungsleitern
auf. Sie sind frequenzabhängig und nehmen mit steigender Frequenz zu. Die magnetischen
Verluste sind in erster Linie von der Spule und dabei insbesondere vom Kernmaterial
abhängig. Die Schaltverluste wiederum treten in den Halbleiterbauelementen, besonders
im Transistor auf und sind stromabhängig. Sie entstehen durch endliche Schaltzeiten, so
dass am Transistor zeitweise Strom und Spannung gleichzeitig fließen bzw. anliegen. Durch
hohe Schaltfrequenzen, also häufiges Umschalten, steigen die Schaltverluste an [5]. Laut
Experimentierbuch soll es möglich sein neben den Gesamtverlusten auch eine Aufgliederung
in die einzelnen Teilverluste vorzunehmen. Darauf wurde in diesem Versuch verzichtet, da
neben einer Vielzahl von Einzelmessungen auch spezielles Equipment nötig gewesen wäre,
z. B. eine variabel einstellbare, elektronische Last zur Veränderung des Ausgangsstroms.
Im Versuch sind bei einer festen Eingangsspannung von 10 V mit Hilfe von Multimetern die
sich einstellenden Eingangs- und Ausgangsströme sowie die Ausgangsspannung gemessen
worden. Dies geschah für insgesamt sechs verschiedene Spulen (drei je Tiefsetzsteller) und
zwei Schaltfrequenzen (fsw1 = 450 kHz, fsw2 = 300 kHz). Am Ausgang wurde ein fester
Ausgangswiderstand von 3,3 Ω für den oberen, beziehungsweise 5,8 Ω für den unteren
Tiefsetzsteller angeschlossen. Grund für die Änderung ist eine zu starke Erhitzung des
Widerstands. Die Ergebnisse sind in den Tabellen 2.1 und 2.2 aufgeführt.
Tabelle 2.1: Spannungen und Ströme für verschiedene Induktivitäten und Schaltfrequenzen
(LM3475)
Ue Ie Ua Ia η
L1
fsw1 10 V 0,42 A 3,331 V 1,017 A 80,17 %
fsw2 10 V 0,41 A 3,3 V 1,015 A 81,7 %
L2
fsw1 10 V 0,44 A 3,31 V 1,016 A 76,49 %
fsw2 10 V 0,42 A 3,302 V 1,015 A 79,80 %
L3
fsw1 10 V 0,43 A 3,310 V 1,017 A 78,29 %
fsw2 10 V 0,41 A 3,302 V 1,015A 81,74 %
10

15. Tabelle 2.2: Spannungen und Ströme für verschiedene Induktivitäten und Schaltfrequenzen
(TPS54160)
Ue Ie Ua Ia η
L1
fsw1 10 V 0,24 A 3,331 V 0,58 A 80,5 %
fsw2 10 V 0,23 A 3,322 V 0,58 A 83,77 %
L2
fsw1 10 V 0,24 A 3,22 V 0,58 A 77,88 %
fsw2 10 V 0,24 A 3,331 V 0,58 A 80,5 %
L3
fsw1 10 V 0,24 A 3,31 V 0,581 A 80,12 %
fsw2 10 V 0,23 A 3,322 V 0,579 A 83,63 %
Mit Hilfe der aufgenommenen Messwerte kann der Wirkungsgrad nach folgender Formel
berechnet werden:
η =
Pab
Pzu
=
Ua · Ia
Ue · Ie
. (2.2)
Auch dieser ist zur besseren Vergleichbarkeit direkt in den Tabellen 2.1 und 2.2 aufgeführt.
Es ist zu erkennen, dass die Wirkungsgrade für alle Frequenzen und Induktivitäten
vergleichbar sind und sich in etwa bei 80 % einpegeln. Es lässt sich eine Abhängigkeit
des Wirkungsgrades von der Schaltfrequenz feststellen. Dabei sinkt der Wirkungsgrad
mit zunehmender Schaltfrequenz. Dies lässt sich sehr wahrscheinlich auf die auftretenden
Schaltverluste in den Halbleiterbauelementen zurückführen. Diese treten auf, da der Strom
den sprunghaften Spannungsänderungen nicht ausreichend schnell folgen kann.
Bezüglich der verschiedenen Spulen lässt sich sagen, dass zwar Unterschiede in den
Wirkungsgraden für verschiedene Spulen auftreten, diese sind aber verhältnismäßig gering
und könnten eventuell auch auf Messfehler zurückzuführen sein. In Tabelle 2.3 sind
beispielsweise die Daten der drei Spulen des ersten Tiefsetzstellers aufgeführt. Ein wirklicher
Zusammenhang zu den Ergebnissen kann auf den ersten Blick nicht hergestellt werden.
Tabelle 2.3: Vergleich der Spulen des LM3475
L1 L2 L3
Modellname WE-TPC-8043 WE-LHMI-7050 WE-PD-7345
Induktivität 100 µH 68 µH 68 µH
Widerstand 270 mΩ 386 mΩ 239 mΩ
Der Grund für die geringen Unterschiede bei verschiedenen Spulen wird jedoch relativ
11

16. schnell klar, wenn man einen Blick ins Experimentierbuch wirft und die Erläuterungen zu
den Spulenverlusten betrachtet. Dort werden diese in einen Gleich- und einen Wechselanteil
aufgeteilt. Der Gleichanteil lässt sich nach folgender Formel bestimmen:
PInd,DC = RLDC · I2
a . (2.3)
Der ohmsche Widerstand der Spulen RLDC ist für den ersten Tiefsetzsteller in der obigen
Tabelle 2.3 einzusehen. Er ist bei der zweiten Spule etwas erhöht, wodurch sich auch der
niedrigere Wirkungsgrad erklären lässt. Die proportionale Abhängigkeit der Spulenverluste
zum Quadrat des Ausgangsstroms sollte bei hohen Ausgangsströmen zu deutlich größeren
Unterschieden für die verschiedenen Spulen führen. Für eine solche Untersuchung bräuchte
man jedoch eine elektronische Last, die nicht zur Verfügung stand. Mit den handelsüblichen
ohmschen Widerständen im Labor kann aufgrund der schnellen Erhitzung leider nicht die
notwendige Variation des Ausgangsstroms vorgenommen werden.
2.3 Untersuchungen zur Ausgangsfilterfunktion mit
verschiedenen Kondensatoren eines Tiefsetzstellers
In diesem Versuch ist der Tiefsetzsteller aus Abbildung 2.1 in Eingangs- und Ausgangsfilter
unterteilt worden. Dies ist in Abbildung 2.7 dargestellt. Ziel dieses Versuches ist die Untersu-
chung der Ausgangsfilterfunktion mittels Ausgangsspannung unter Nutzung verschiedener
Induktivitäten, eines Elektrolytkondensators (C17) sowie eines Kermaikkondensators (C18).
Die relevanten Bauelemente sind im Schaltplan A.3 gekennzeichnet. Der Kondensator
Ca ist ein wichtiges Element des Ausgangsfilters, der die Ausgangsspannung beeinflusst.
Somit kann gewährleistet werden, dass die maximale Amplitude der Ausgangsspannung
um höchstens 1 % vom entsprechenden Mittelwert abweicht.
Abbildung 2.7: Aufteilung des Tiefsetzstellers [1]
Laut Lehrbuch ist gleichzeitig mit einem Vier-Kanal-Oszilloskop die Eingangsspannung, die
Schaltfrequenz, der Spitze-Spitze-Spulenstrome (∆iLpp) und die Spitze-Spitze-Amplitude
der Aussgangspannung zu messen. Die Messung soll je einmal für die Induktivitäten
12

17. L4 und L5 unter Zuschaltung eines Kondensators erfolgen. Dabei ist besonders auf die
Welligkeit und auf mögliche Verzerrungen des Spulenstromes und der Ausgangsspannung zu
achten. Aus den gemessenen Werten soll der äquivalente Reihenwiderstand des Tantalum-
Kondensators (Elektrolytkondensator) und die Kapazität des Keramikkondensators mittels
Formel 2.4 rechnerisch ermittelt werden.
Ca =
∆iLpp
8∆Uapp · fsw
(2.4)
Bei einem Elektrolytkondensator sind Ausgangsstrom- und Spannung in Phase, bei einem
Keramikkondensator nicht. Dies ist in den Abbildungen 2.8 und 2.9 erkennbar. Beide
Abbildungen entsprechen idealen Bedingungen, d. h.:
Uin=10 V Eingangsspannung
Ua=3,3 V Ausgangsspannung
iL=400 mA Laststrom
fsw=500 kHz Schaltfrequenz
L=10 mH Induktivität
CEl= 220 µF Kapazität des Elektrolytkondensators
CKer=10 µF Kapazität des Keramikkondensator.
Die Abbildungen 2.8 und 2.9 zeigen, dass bei gleichem pulsierenden Spulenstrom ver-
schiedene pulsierende Ausgangsspannungskurven resultieren. In Abbildung 2.9 ist eine
Phasenverschiebung von 90 ◦
zu sehen, die auf den geringen Innenimpedanz des Keramik-
kondensators Zc zurückzuführen ist. Diese lässt sich mittels (2.5) berechnen:
Zc = Rc + jXc. (2.5)
Der Blindanteil Xc der Impedanz lässt sich wie folgt errechnen:
Xc =
1
2π · Ca · fsw
. (2.6)
(2.7) zeigt, dass der Blindanteil der Impedanz des Keramikkondensators viel größer ist als
sein Wirkanteil, wodurch die Kapazität direkt mittels (2.4) errechnet werden kann.
Keramikkondensator:
Ri
1
2π · fsw · Ca
(2.7)
13

18. Bei einem Elektrolykondensator erfolgt keine Phasenverschiebung, da dessen Innenwi-
derstand, wie in (2.8) zu sehen, sehr hoch im Vergleich zum Blindanteil der Impedanz
ist.
Elektrolytkondensator:
Ri
1
2π · fsw · Ca
(2.8)
Die Kapazität des Elkos lässt sich also nicht direkt ermitteln. In diesem Fall hängt die
Ausgangsspannung des Ausgangsfilters von dem Innenwiderstand des Elkos ab:
∆Uapp = Ri · ∆iLpp. (2.9)
Abbildung 2.8: Idealer Ausgangsstrom und ideale Ausgangsspannung eines Elektrolytkon-
densators [1]
14

19. Abbildung 2.9: Idealer Ausgangsstrom und ideale Ausgangsspannung eines Keramikkon-
densators [1]
In der Realität kann jedoch nicht erwartet werden, dass die Bauelemente ideale Eigenschaf-
ten besitzen. Es müssen parasitäre Effekte durch zum Beispiel Induktivitäten, Kapazitäten
oder Zuleitungen beachtet werden. Die in der Realität zu erwartenden Verläufe sind in der
Abbildung 2.10 aufgeführt.
Abbildung 2.10: Zu erwartender Ausgangsstrom und zu erwartende Ausgangsspannung
bei einer realen Messung mittels Oszilloskop [1]
15

20. Im Rahmen dieser Arbeit ist überprüft worden, ob die zuvor erwähnten Erwartungen
(Phasenverschiebung) mit der Realität übereinstimmen. Der Versuchsaufbau ist in Abbil-
dung 2.11 dargestellt. Auch in diesem Versuch ist ein Zwei-Kanal-Oszilloskop verwendet
worden. Auf eine Analyse der Ausgangsspannung in Abhängigkeit des Kondensators wurde
verzichtet.
+ CH1
CH2
Abbildung 2.11: Versuchsaufbau des dritten Versuches (nach [1])
Die in den Abbildungen 2.12 und 2.13 dargestellten Messwerte bestätigen die Theorie und
die Lehrbuchabbildung 2.10.
16

21. 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5
Zeit, t in s
-6
-4
-2
0
2
4
6
Strom,iLinA
3.25
3.3
3.35
3.4
Spannung,UoutinV
Elektrolytkondensator
Abbildung 2.12: Gemessener Ausgangsstrom und gemessene Ausgangsspannung des Elek-
trolytkondensators
0 0,5 1 1,5 2 2,5 3 3,5 4 4,5
Zeit, t in s
-6
-4
-2
0
2
4
6
Strom,iLinA
3.25
3.3
3.35
3.4
Spannung,UoutinV
Keramikkondensator
Abbildung 2.13: Gemessener Ausgangsstrom und gemessene Ausgangsspannung des Kera-
mikkondensators
Die unterschiedlichen Spannungsverläufe, insbesondere die Phasenverschiebung zwischen
Strom und Spannung resultieren wie bereits erklärt aus den zwei verschiedenen Konden-
satortypen. Ein Keramikkondensator besitzt mindestens zwei Keramikoxidschichten als
Dielektrikum [6]. Dahingegen besitzen Elektrolytkondensatoren nur einen festen Kon-
densatorbelag sowie einen flüssigen Elektrolytbelag [7]. Ein weiterer Unterschied ist der,
17

22. dass die Polung bei Keramikkondensatoren irrelevant ist. Im Gegensatz dazu spielt diese
bei Elektrolytkondensatoren eine Rolle, da bei einem Nichtbeachten Defekte entstehen
würden.
2.4 Untersuchungen zur Eingangsfilterfunktion verschiedener
Induktivitäten eines Tiefsetzstellers
Dieser Versuch ist das Analogon zum vorherigen mit dem Unterschied, dass jetzt der
Eingangsfilter (Abbildung 2.7) analysiert wird. Dabei findet eine Untersuchung des Ein-
flusses der Induktivität auf den Eingangsstrom statt. Wenn bei einem Eingangsfilter der
Ausgangswiderstand nicht auf den Eingangswiderstand angepasst ist, das heißt wenn Rout
ungleich Rin, kann dies zu einer Instabilität des Tiefsetzstellers führen. Eine effektive
Möglichkeit dem entgegenzuwirken ist das Hinzufügen eines zusätzlichen LR-Zweiges wie
in folgender Abbildung 2.14 aufgezeigt ist.
Abbildung 2.14: Dämpfungsprinzip: Tiefsetzsteller mit RL-Zweig [1]
Beide Eingangsspulen (d. h. die ursprüngliche Spule Lf und die Spule des zusätzlichen
Zweiges Ld) sind sowohl in Abbildung 2.2 als auch im Schaltplan des Anhangs in A.4
gekennzeichnet. In der Theorie reicht es nur einen Widerstand parallel zu schalten, um
eine Dämpfung beim Schalten zu erreichen, aber dies würde zu einer Verringerung des
Wirkungsgrades führen. Die Induktivität führt zu einem Ausgleich zwischen Wirkungs-
und Dämpfungsgrad. Auf der Leiterplatte handelt es sich um die Spulen L7 bis L10, welche
in der Abbildung 2.2 mit Pfeilen gekennzeichnet sind.
Die Wirkung der zusätzlichen Spulen ist anhand der folgenden Funktionen in 2.15 ver-
deutlicht. Die rote Kurve stellt das ungefilterte System, die blaue und die grüne Kurve
stellen das gefilterte System durch zusätzliche Spulen dar.
18

23. Abbildung 2.15: Filterung mit den Spulen L7 und L8 [1]
Das Ziel dieses Versuchs ist es, die Performance und Funktionalität der beiden Eingangsfil-
ter der oberen Leiterplatte LM3475 und der unteren Leiterplatte TPS54160 miteinander zu
vergleichen und dabei die Wirkungsweise des zusätzlichen LR-Zweiges mittels Messungen
aufzuzeigen und nach Möglichkeit die Theorie zu bestätigen. Dabei soll der Eingangs-
spitzenstrom unter Anschluss verschiedener Eingangsspannungen und Lastwiderstände
gemessen werden. Da hier erneut eine elektronische Last zum Variieren des Laststromes
nötig gewesen wäre und ist im Rahmen dieser Arbeit auf diesen wie auch auf Versuch fünf
und sechs verzichtet worden. In Experiment fünf geht es um die Analyse der Induktivität
im lückenden- und nichtlückenden Betrieb. Im sechsten Experiment soll eine Pulsweiten-
modulation des Spitzenstroms durch Nutzung eines Komparators und Verstärkers erfolgen.
Wie bereits in der Einleitung erläutert, war das Hauptziel dieser Arbeit die Analyse des
Boards und seiner Versuche auf Pädagogiktauglichkeit. Für die Versuche fünf und sechs
sind tiefgründigere Kenntnisse notwendig, die z.B. Schülerpraktikant*innen noch nicht
haben können.
Da diese Arbeit im Rahmen der Lehrveranstaltung EMV-Messtechink absolviert wurde,
soll im Folgenden jedoch noch auf das Thema Störaussendung näher eingegangen werden.
2.5 EMV-Störaussendung des Experimentierboards
In der elektromagnetischen Verträglichkeit ist die Störaussendung ein gebräuchlicher Begriff.
Diese beschreibt die Eigenschaft eines Geräts Störsignale auszusenden, die weitere Geräte
in der Nähe beeinflussen könnten. Demnach ist dies eine unerwünschte Eigenschaft, die so
gut es geht vermieden werden sollte.
Auch das Experimentierboard innerhalb dieses Versuchs sendet Störsignale aus, diese
konnten mit Hilfe eines Oszilloskops gemessen werden. Die Messung ist in Abbildung 2.16
19

24. dargestellt und die wichtigen Details sind mit grünen Rechtecken hervorgehoben. Es ist zu
erkennen, dass der gelbe Kanal ohne eine elektrisch leitfähige Verbindung auf den grünen
Kanal überkoppelt.
Abbildung 2.16: Messung der Störaussendung des Experimentierboards mit Hilfe eines
Oszilloskops.
Um zu verstehen, wie dieses Phänomen zu Stande kommen (und vermieden werden) kann,
ist es nötig die Grundlagen der verschiedenen Kopplungsmöglichkeiten zu betrachten.
Dies soll im Folgenden mit Hilfe der Schaltungen der Abbildungen 2.17 - 2.19 geschehen.
Zur Vereinfachung werden jeweils nur zwei verschiedene Leiter betrachtet die aufeinander
einwirken. In der Realität ist es jedoch auch möglich, dass mehr als zwei Leiter vorhanden
sind.
20

25. uG1(t)
RG1
RL1
RKoppel
LKoppel
uG2(t)
RG2
RL2
Abbildung 2.17: Veranschaulichung der galvanischen Kopplung.
Zuerst wird die galvanische Kopplung betrachtet. Diese kommt zu Stande, wenn zwei
Stromkreise einen gemeinsamen Bezugsleiter besitzen. Oft ist dies die Verbindung zur elek-
trischen Masse. In diesem Fall müssen der Koppelwiderstand und die Koppelinduktivität,
an denen ein Spannungsabfall (siehe Gleichung (2.10)) stattfindet beachtet werden.
Für die Entkopplung zweier Stromkreise ist eine Potentialtrennung notwendig. Dies kann
zum Beispiel mittels Optokopplern oder Transformatoren geschehen. Weiterhin besteht
die Möglichkeit zwei separate Leiter zu nutzen statt eines Gemeinsamen.
Eine Verkopplung sollte so gut es geht vermieden werden. Das kann durch dicke Lei-
terquerschnitte (kleiner Koppelwiderstand) und kurze Leiter (kleine Koppelinduktivität)
geschehen.
u(t) = RKoppel · i(t) + LKoppel ·
di(t)
dt
(2.10)
21

26. uG1(t)
RG1
RL1
uG2(t)
RG2
RL2
CKoppel
CMasse1 CMasse2
Abbildung 2.18: Veranschaulichung der kapazitiven Kopplung.
Die zweite Kopplungsmöglichkeit ist die kapazitive Kopplung, die durch einen Kondensator
zwischen zwei Leitern, sowie zwischen einem Leiter und der Masse veranschaulicht werden
kann. Durch die verschiedenen Potentiale auf den Leitungen findet eine unerwünschte
Energieübertragung statt. In diesem Fall wird ein Strom in die jeweils andere Leitung
eingeprägt (siehe Gleichung (2.11)). Die parasitären Kapazitäten werden auch als Streuka-
pazitäten bezeichnet.
Eine Minimierung des Effekts kann zum Beispiel durch große Abstände zwischen den
Leitungen, Schirmung oder langsame Spannungsänderungen erfolgen.
i(t) = CKoppel ·
du(t)
dt
(2.11)
22

27. uG1(t)
RG1
MGegen
i1(t)
RL1
uG2(t)
RG2
MGegen
RL2
Φ12(t)
Abbildung 2.19: Veranschschaulichung der induktiven Kopplung.
Die dritte Kopplungsmöglichkeit ist die induktive Kopplung, die durch parasitäre Gegenin-
duktivitäten veranschaulicht werden kann. Sie beschreibt die magnetische Beeinflussung
zweier benachbarter Stromkreise und ist vergleichbar mit der Funktionsweise eines Trans-
formators. Das bedeutet, durch eine Stromänderung im ersten Kreis wird eine Spannung
in den zweiten Kreis induziert (siehe Gleichung (2.12)).
Minimiert werden kann diese Kopplungsart zum Beispiel durch möglichst kurze Leitungen,
große Abstände zwischen den Leitern oder eine symmetrische Leiteranordnung (Aufhebung
der Felder).
uind(t) = MGegen ·
di1(t)
dt
(2.12)
Des Weiteren existiert auch die sogenannte Strahlungskopplung. In dieser Variante sind
das magnetische und elektrische Feld untrennbar miteinander verbunden. Da diese nur bei
höheren Frequenzen auftritt, soll eine Beschreibung nicht Bestandteil dieses Dokuments
sein.
Abschließend stellt sich die Frage: „Um was für eine Art Einkopplung handelt es sich in
diesem Fall?“
Dies kann mittels Ausschlussverfahren ermittelt werden. Aus den Ausführungen zur
galvanischen Kopplung ist bereits bekannt, dass diese nur auftritt wenn zwei Stromkreise
einen gemeinsamen Bezugsleiter besitzen. Da das auf diesen Fall nicht zutrifft, entfällt die
erste Variante.
Bei der Überlegung, ob es sich um eine induktive Einkopplung handelt ist zu beachten,
dass der Eingang des Oszilloskops hochohmig ist. Aus diesem Grund kann kein Stromfluss
im zweiten Oszilloskop-Kanal stattfinden und diese Variante ausgeschlossen werden.
23

28. Daher kann es sich hier nur um eine kapazitive Einkopplung handeln. Dies wird auch
deutlich, wenn der Abstand zwischen Störquelle und Messspitze verändert wird (siehe
dazugehöriges Video auf dem Twitter-Account), da sich dann auch die eingekoppelte
Spannungsamplitude ändert.
24

29. 3 Fazit
Abschließend soll ein Fazit zum Experimentierboard gezogen werden. Die Platine ist
entwickelt worden, um Studierenden die Möglichkeit zu geben, an einem DC-DC-Wandler
selbstständig zu arbeiten und dabei insbesondere den Einfluss von Leistungsinduktivitäten
zu erforschen. Damit sollen sie ihre theoretischen Kenntnisse aus dem Studium praktisch
validieren und erweitern können [1]. Dafür ist ein äußerst umfangreiches Experimentierbuch
zur Verfügung gestellt worden. Dieses beinhaltet in der Theorie alles, was Studierende
benötigen, um die insgesamt sechs Experimente selbstständig durchführen zu können. Zu
jedem Versuch gibt es einen ausführlichen Theorieteil, genaue Anweisungen zur Vorge-
hensweise (inklusive Schaltpläne, Messaufbauten, etc.) und sogar Messergebnisse und eine
Auswertung.
Der Umfang des bereitgestellten Materials hat Vor- und Nachteile. Auf der einen Seite er-
möglicht er interessierten Tester*innen ganz unterschiedlicher Erfahrung und Qualifikation
mit dem Board zu arbeiten und Versuche durchzuführen. Während Studienanfänger*innen
oder sogar Schüler*innen schon durch wenig Stecken und Drehen erste Ergebnisse am
Oszilloskop sehen können (z.B. eine Änderung des Tastgrads durch eine Veränderung der
Schaltfrequenz), können sich auch erfahrene Studierende oder Absolvent*innen viele Stun-
den mit dem Board beschäftigen, gerade da auch der Theorieteil sehr tief in die Materie
geht (z.B. werden sieben verschiedene Komponenten der Verlustleistung beschrieben).
Diese Fülle an Informationen und Möglichkeiten geht aber auch zu Lasten der der Über-
sichtlichkeit und kann insbesondere bei Studienanfänger*innen und vor allen Dingen bei
Schüler*innen eine abschreckende Wirkung entfalten. Die vier bis fünf Seiten mit klein-
geschriebener Theorie in technischem Englisch und einer Vielzahl von Formeln sind für
das Verständnis und eine erfolgreiche Durchführung der Experimente oft gar nicht not-
wendig. Die bereitgestellten Messwerte und Auswertungen ermöglichen eine selbstständige
Kontrolle, könnten aber auch der Motivation selber etwas entdecken zu wollen, ein wenig
abträglich sein.
Beim praktischen Durchführen der Versuche gab es gerade zu Beginn immer wieder kleinere
und größere Schwierigkeiten die benötigten Anschlüsse zu finden. Auch das ist der Fülle
an Informationen geschuldet, die die Tester*innen gerade zu Beginn regelrecht erschlagen
kann. Vielleicht hätte hier eine Reduzierung der Messpunkte und Anschlüsse helfen können.
25

30. Mit steigender Experimentiererfahrung steigt allerdings auch schnell die Lernkurve und
viele Schritte wiederholen sich, so dass der Umgang mit der Platine sicherer wird.
Der größte Kritikpunkt am Board ist das vorausgesetzte Equipment, das sich so wohl nur in
wenigen Universitätslaboren finden lassen wird. Für fast jeden Versuch wird beispielsweise
eine elektronische, variabel einstellbare Last vorausgesetzt, um den Ausgangsstrom frei
verändern zu können. Auch ein Vier-Kanal-Oszilloskop sowie vier Multimeter werden
regelmäßig erwartet. Gerade ein Fehlen der Last schränkt die Möglichkeiten zum Experi-
mentieren ein.
Insgesamt punktet das Experimentierboard durch seinen Umfang und der Vielfältigkeit
seiner Experimente. Studienanfänger*innen und Schüler*innen könnten aber gerade deswe-
gen und aufgrund der etwas unintuitiven Handhabung zunächst etwas überfordert sein.
Um das Board in seiner Gänze kennenlernen zu können, wird Spezialequipment benötigt
und es werden solide Kenntnisse der Leistungselektronik sowie viel Zeit empfohlen.
26

31. Literaturverzeichnis
[1] Würth Elektronik: PMLK Learning Kit Experiment Buch. Würth Elektronik,
2020
[2] Texas Instruments: LM3475HystereticPFET Buck Controller.
https://www.ti.com/lit/ds/symlink/lm3475.pdf?ts=1600610132349&ref_url=
https%253A%252F%252Fwww.ti.com%252Fproduct%252FLM3475, . – Aufgerufen am:
2020-08-20
[3] F. Müller, P. Vaske: Elektrische Maschinen und Umformer. Teubner Verlag, 1970
[4] J. Böker: Laborpraktikum: Versuch Tiefsetzsteller.
https://ei.uni-paderborn.de/fileadmin/elektrotechnik/fg/lea/Lehre/
Laborpraktikum/Dokumente/Tiefsetzsteller.pdf, . – Aufgerufen am: 2020-09-15
[5] Wikipedia: Schaltverluste.
https://de.wikipedia.org/wiki/Schaltverluste, . – Aufgerufen am: 2020-09-15
[6] Elektronik-Kompendium: Keramikkondensatoren / Kerko.
http://www.elektronik-kompendium.de/sites/bau/0206111.htm, . – Aufgerufen
am: 2020-09-19
[7] Elektronik-Kompendium: Elektrolytkondensatoren.
http://www.elektronik-kompendium.de/sites/bau/0206113.htm, . – Aufgerufen
am: 2020-09-19
27

32. Selbstständigkeitserklärung
Hiermit versichern wir, Christina Bertram, Vincent Szameitat und Pierre Bolz, die vor-
liegende Arbeit selbstständig und unter ausschließlicher Verwendung der angegebenen
Literatur und Hilfsmittel erstellt zu haben.
Magdeburg, den 21. September 2020
28

33. A Schaltpläne
Abbildung A.1: In diesem Schaltungsausschnitt sind die Spulen (Induktivitäten) zur Analy-
se der physischen und charakteristischen Beeinflussung, gekennzeichnet. [1]
29

34. Abbildung A.2: In diesem Schaltungsausschnitt sind die Spulen gekennzeichnet, mit denen
die Verluste ermittel werden. [1]
30

35. Abbildung A.3: In diesem Schaltungsausschnitt sind die Spulen und die Kondensatoren
des Ausgangsfilters gekennzeichnet. [1]
Abbildung A.4: In diesem Schaltungsausschnitt sind die ursprünglichen Spulen und die
Spulen des zusätzlichen Zweiges des Eingangsfilters gekennzeichnet [1]
31

36. Abbildung A.5: In diesem Schaltungsausschnitt sind die Jumper gekennzeichnet [1]
32

37. Abbildung A.6: Darstellung des kompletten Schaltplans der Platine [1]
33