Die Vorlesung "elektrische Maschinen" von Prof. Dr.-Ing. G. Ackermann an der Technischen Universität Hamburg-Harburg behandelt ausführlich die Grundlagen, den Aufbau und die Funktionsweise von elektrischen Maschinen, einschließlich Gleichstrom-, Drehfeld- und Synchronmaschinen. Das Dokument liefert strukturierte Inhalte mit Formelzeichen, technischen Begriffen und spezifischen Berechnungen, ergänzt durch Übungsaufgaben. Änderungen gegenüber einer früheren Ausgabe umfassen die Hinzufügung von Aufgaben zu Asynchronmotoren und kleinere Korrekturen.

1. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 1 von 108
Technische Universität Hamburg-Harburg
Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann Eißendorfer Str. 38, 21073 Hamburg
Tel.: 040/428 78-4204
Manuskript der Vorlesung
„Elektrische Maschinen“
Prof. Dr.-Ing. G. Ackermann
Änderungen gegenüber Stand 10/09:
Aufgabe 8 (Asynchronmotoren) hinzugekommen; kleinere Korrekturen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

2. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 2 von 108
Inhalt
1 FORMELZEICHEN, KONVENTIONEN 4
2 GLEICHSTROMMASCHINEN 5
2.1 Aufbau 5
2.2 Wirkung der Erregerwicklung 6
2.3 Kraftwirkung 7
2.4 Mechanische Abmessungen 14
2.5 Feldlinienbild, Ankerrückwirkung 15
2.6 Kompensations- und Wendepolwicklungen 16
2.7 Betriebsverhalten und Kennlinien 18
2.7.1 Spannungsgleichung und Drehmomentgleichung 18
2.7.2 Fremderregung, Permanenterregung 19
2.7.3 Reihenschlussverhalten 22
2.7.4 Wechselstrommotoren 24
3 DREHFELDMASCHINEN 24
3.1 Drehfelder in elektrischen Maschinen, Drehmoment und Abmessungen 24
3.1.1 Zum Aufbau von Drehfeldmaschinen 24
3.1.2 Grundprinzip der Drehfeldbildung 25
3.1.3 Beschreibung des Drehfeldes 26
3.1.4 Drehmoment, Strombelag, Abmessungen 29
3.2 Asynchronmaschinen 32
3.2.1 Besondere Formelzeichen und Begriffe 32
3.2.2 Aufbau der Ständer- und Läuferwicklung, Begriffe 32
3.2.3 Läuferspannungsgleichung 33
3.2.4 Ortskurve des Läuferstromes, Ersatzschaltbilder 37
3.2.5 Stromortskurve der Asynchronmaschine (Heyland-Kreis) 39
3.2.6 Normierung der Stromortskurve 41
3.2.7 Drehmoment-Drehzahl- und Strom-Drehzahl-Kennlinien 42
3.2.8 Aufteilung der Luftspaltleistung 43
3.2.9 Polumschaltung, Schleifringläufer, Käfigläufer 45
3.2.10 Stromverdrängungsläufer 46
3.2.11 Mechanisches Modell für den Asynchronmotor 49
3.2.12 Verluste von Asynchronmotoren und mechanischen Kupplungen bei
Beschleunigungsvorgängen 50
3.2.13 Betrachtung zur Größenordnung der Verlustenergie in einem Hebezeugmotor
für ein Frachtschiff 54
3.2.14 Anmerkungen zu instationären Betriebszuständen 60
3.2.15 Einphasiger Asynchronmotor 62
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

3. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 3 von 108
3.3 Synchronmaschinen 63
3.3.1 Grundsätzliche Wirkungsweise und Eigenschaften 63
3.3.2 Konstruktive Ausführung, Anwendungen 66
3.3.3 Betriebsverhalten, Kennlinien 68
3.3.4 Ortskurve des Ständerstromes 72
3.3.5 Drehmomentbildung 74
3.3.6 Betrieb der Synchronmaschine am Netz 75
3.4 Antriebe mit Frequenzumrichter 77
3.4.1 Pulswechselrichter 77
3.4.2 Leistungsflüsse bei Motorbetrieb und bei Bremsbetrieb 79
3.4.3 Zur Regelung und Steuerung 80
4 SONDERFORMEN ELEKTRISCHER MASCHINEN 82
4.1 Schrittmotoren 82
4.2 Linearmotoren 84
4.3 Drehstrom-Lichtmaschine für Pkw`s/Lkw`s 86
4.4 Antrieb für einen kleinen Lüfter (z. B. in Rechnern) 86
4.5 Autotachometer, Drehzahlmesser usw. 87
4.6 Scheibenmotor 88
5 ZUR BERECHNUNG DES DYNAMISCHEN VERHALTENS VON
DREHFELDMASCHINEN 89
5.1 Voraussetzungen 89
5.2 Idee der Berechnungsweise 89
5.3 1. Schritt: Transformation auf ein 2-phasiges a-b-System 90
5.4 Besonderheiten bei der Rechnung in normierten Größen 92
5.5 2. Schritt: Transformation von a-b in ein verdrehtes x-y-System 92
5.6 3. Schritt: Die Gleichungen der Synchronmaschine 93
5.7 Anwendung auf die Asynchronmaschine 96
6 ÜBUNGSAUFGABEN 98
6.1 Allgemeines, Grundlagen 98
6.2 Gleichstrommaschine 99
6.3 Asynchronmaschine 102
6.4 Synchronmaschine 106
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

4. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 4 von 108
1 Formelzeichen, Konventionen
a) Großbuchstaben: zeitlich konstante Größen
Kleinbuchstaben: zeitlich veränderliche Größen
b) Bei Wechsel- und Drehstrom sind U, I die Effektivwerte
c) _ (Unterstrich) markiert komplexe Größen
d) Bei Drehstrom ist die Spannung zwischen den Leitern gemessen, der Strom ist der Leiter-
strom.
e) Das einphasige Ersatzschaltbild bei Drehstrom ist immer auf eine Sternschaltung bezogen.
Häufig verwendete Indizes:
o Leerlauf
L Luftspalt
n Nennwert
N Netz
A Anker der Gleichstrommaschine
1 Stator-/Ständergröße
2 Rotor-/Läufergröße
f Feld, Erreger
σ Streuinduktivität
h Hauptinduktivität
p Pol
e Erreger, Feld
P Wirk...
Q Blind...
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

5. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 5 von 108
2 Gleichstrommaschinen
2.1 Aufbau
Quelle: ABB-Cat DMI 99-02 Klemmkasten
Bürsten
Rotor- (Anker-)
Wicklung
Kommutator
Feldwicklung
Abbildung 2.1: Schnitt durch eine Gleichstrommaschine
Joch
Erregerwicklung
Windungszahl Ne
r Anker mit
Ankerwicklung
Polschuhe
F
Pol
Abbildung 2.2: Schematischer Querschnitt durch einen Gleichstrommotor
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

6. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 6 von 108
Der Ständer von Gleichstrommaschinen, auch Magnetgestell genannt, besteht aus einem Jochring
aus Stahl, ausgeprägten Hauptpolen mit Polkernen und Polschuhen aus Elektroblech und der auf
den Polkernen sitzenden Erregerwicklung (Feldwicklung).
Bis zu einer Nennleistung von 20 kW werden auch permanenterregter Gleichstrommaschinen ge-
baut. Bei diesen sind die Erregerwicklungen und ihre Polkerne durch Dauermagneten ersetzt. Der
Läufer von Gleichstrommaschinen, meist Anker genannt, besteht aus einer Stahlwelle mit aufge-
presstem Läuferblechpaket aus Elektroblech. Er trägt die in Nuten befindliche Ankerwicklung und
einen Stromwender.
2.2 Wirkung der Erregerwicklung
Abbildung 2.3 zeigt schematisch das durch die Erregerwicklung erzeugte magnetische Feld. Der
Luftspalt zwischen Rotor und Stator habe in radialer Richtung die Länge d. Nach dem Durchflu-
tungsgesetz ergibt sich für den Erregerstrom If die Flussdichte im Luftspalt:
µ o ⋅ 2N e ⋅ If
BL =
2d + lFe / µr
Ne ist die Windungszahl einer der beiden Erregerspulen und lFe ist die Länge der Feldlinien im
Eisen. Oft ist
2d >> lFe/µr,
dann kann der zweite Term im Nenner entfallen oder man rechnet ersatzweise mit einem etwas
vergrößerten Luftspalt. Damit ist die Flussdichte einfacher:
N e ⋅ If
BL = µo · (2.1)
d
Der magnetische Fluss folgt unter Annahme eines homogenen Feldes und unter Vernachlässigung
von Feldverzerrungen an den Rändern der Polschuhe zu:
Φ = BL · lp · bp (2.2)
lp ist dabei die Länge des aktiven Bereiches in axialer Richtung.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

7. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 7 von 108
Pol 2
bp
Pol 1
lp
bp
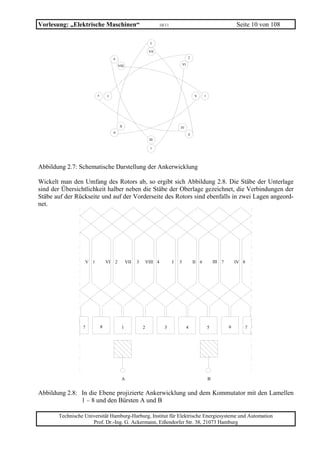
Abbildung 2. 3: Schematische Darstellung zum Verlauf des Erregerfeldes
Ne ⋅ If Θ
B = µo = µo · (2.3)
d d
Bis zu einer Flussdichte von etwa 1,5 T ist die Flussdichte proportional zu dem Erregerstrom If.
B[T]
2 Bei einer Flussdichte von etwa 1,5 T beginnt die Eisensätti-
gung, d. h. zur Vergrößerung des Flusses ist eine überproporti-
1,5
onale Erhöhung des Erregerstromes erforderlich. Eine Fluss-
1 dichte von etwa 2,2 T kann in üblichen Eisenarten erreicht
werden.
0,5
H
Abbildung 2.4: Magnetisierungskennlinie mit Sättigung
2.3 Kraftwirkung
Auf einen Strom führenden Leiter in einem Magnetfeld wird eine Kraft senkrecht zum Leiter
und senkrecht zu dem magnetischen Feld ausgeübt.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

8. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 8 von 108
BL i
lp
BL F F, v
u
Abbildung 2.5: Kraftwirkung auf einen stromdurchflossenen Leiter
Mit den in Abbildung 2.5 eingetragenen Zählpfeilen ist nach den Grundgesetzen der Elektrotech-
nik:
F = BL · i · lp (2.4)
Bei einer Bewegung des Leiters mit der Geschwindigkeit v wird in dem Leiter eine Spannung u
induziert, die nach dem Induktionsgesetz durch die zeitliche Änderung des magnetischen Flusses
in der Leiterschleife bestimmt ist:
dΦ
ui = +
dt
Für das Vorzeichen der Spannung gilt die Lenz`sche Regel, nach der ein aus der induzierten
Spannung resultierende Stromfluss der Flussänderung entgegenwirkt. Die Bewegung des Leiters
verkleinert die Fläche der Leiterschleife und somit auch den Fluss. Die induzierte Spannung muss
also einen Strom erzeugen können, der den Fluss verstärkt.
Mit den Angaben in Abbildung 2.5 ist
dΦ
= - BL · lp · v
dt
ui = - BL · lp · v
Ordnet man auf dem Rotor des Eisenkreises nach Abbildung 2.6 parallel zur Achse isolierte Stäbe
in Nuten an und sorgt dafür, dass in ihnen unter dem oberen Pol Ströme entgegengesetzt zu den
Strömen unter dem unteren Pol fließen, so wird ein Drehmoment auf den Rotor ausgeübt. Es gel-
ten die gleichen Überlegungen, die zu Gleichung 2.4 geführt haben. Die resultierenden Kräfte
greifen aber keinesfalls an den stromdurchflossenen Leitern an, sondern sie wirken zum großen
Teil auf das Eisen zwischen den Nuten.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

9. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 9 von 108
Pol 2
r
F
Pol 1
Abbildung 2.6: Zur Drehmomentbildung in einer Gleichstrommaschine
Die in Abbildung 2.6 gezeigte Maschine hat eine Rotorwicklung mit N Windungen, bei der je
zwei (gegenüberliegende) Stäbe zu einer Windung zusammengefasst sind.
Bringt man auf den Rotor mehrere Windungen gleichmäßig verteilt an (Abbildung 2.7), so muss
man beachten, dass jede Windung einen „linken“ Stab (I; II; III;...) und einen „rechten“ Stab (1; 2;
3;...) hat. Aus Symmetriegründen müssen die linken Stäbe über den ganzen Umfang verteilt wer-
den und die rechten Stäbe müssen dann ebenfalls über den ganzen Umfang verteilt sein.
Man kann die Stäbe von je zwei Windungen in einer Nut übereinander anordnen. Dann sind ent-
weder alle linken Stäbe unten und alle rechten Stäbe oben in den Nuten oder umgekehrt. Verbin-
det man z. B. auf der Hinterseite des Rotors jeweils die zusammengehörigen Stäbe I1; II2; III3 zu
Windungen und schaltet auf der Vorderseite alle Windungen hintereinander durch jeweils eine
Verbindung I2; II3; III4, so entsteht eine symmetrische Wicklung, bei der alle Windungen hin-
tereinander geschaltet sind.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

10. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 10 von 108
3
VII
4 2
VIII VI
5 I V 1
II IV
6
8
III
7
Abbildung 2.7: Schematische Darstellung der Ankerwicklung
Wickelt man den Umfang des Rotors ab, so ergibt sich Abbildung 2.8. Die Stäbe der Unterlage
sind der Übersichtlichkeit halber neben die Stäbe der Oberlage gezeichnet, die Verbindungen der
Stäbe auf der Rückseite und auf der Vorderseite des Rotors sind ebenfalls in zwei Lagen angeord-
net.
V 1 VI 2 VII 3 VIII 4 I 5 II 6 III 7 IV 8
7 8 1 2 3 4 5 6 7
A B
Abbildung 2.8: In die Ebene projizierte Ankerwicklung und dem Kommutator mit den Lamellen
1 – 8 und den Bürsten A und B
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

11. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 11 von 108
Bringt man an die Stabverbindungen auf der Vorderseite Kontakte 1; 2;... an, so entsteht ein mit
dem Rotor umlaufender Kommutator. Stillstehende, mit dem Stator der Maschine mechanisch fest
verbundene Kontakte für die Stromzuführung zum Rotor („Bürsten“) seien A und B. Sie sind um
180° gegeneinander versetzt.
Der über eine Bürste der Rotorwicklung zufließende Strom teilt sich in zwei gleich große Ströme
auf die beiden Wicklungshälften auf. Dadurch fließen in den beiden Sektoren zwischen den Bürs-
ten, also unter den beiden Polen der Maschine alle Ströme in gleicher Richtung (Abbildung 2.9).
Pol 1 Pol 2
7 8 1 2 3 4 5 6 7
i i
A B
Abbildung 2.9: Zur Wirkungsweise des Kommutators: Trotz Rotation des Ankers ist die Strom-
richtung unter den Polen konstant.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

12. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 12 von 108
Man kann die einzelnen Windungen der Rotorwicklung als Teilwicklungen betrachten und ein
Schaltschema (Abbildung 2.10) zeichnen.
Es ergibt sich ein geschlossener Kreis aus den einzelnen Teilwicklungen, in diesem Kreis kann
kein umlaufender Strom fließen, da die Summe der induzierten Spannungen im Kreis null ist. Der
Strom i fließt über die Bürste A und teilt sich in zwei Ströme i/2 auf, einer fließt gleichsinnig, der
andere gegensinnig durch jeweils eine Gruppe von Teilwicklungen. Beide Ströme vereinigen sich
am gegenüberliegenden Punkt und fließen durch die Bürste B ab.
II 3
2 III
I i/2 4
1 IV
VIII 5
A B
8 i/2 V
VII 6
7 VI
i
u
A B
Abbildung 2.10: Stromaufteilung in der Wicklung durch den Kommutator
Die Rotorwicklung besteht also von den Klemmen A, B gesehen aus zwei parallelen Zweigen. Die
Einzelwicklungen werden in beiden Zweigen durch die Drehung des Rotors zyklisch weiterge-
schaltet. Dadurch kehrt sich die Stromrichtung in jeder Teilwicklung bei jeder halben Umdrehung
um.
Der Kommutator mit Bürsten wirkt also wie ein Wechselrichter, der den zufließenden Gleichstrom
in Wechselströme umwandelt und den Teilwicklungen zuführt.
Man erkennt aus den Abbildungen 2.6 und 2.9, dass eine räumliche feststehende Anordnung von
Strömen entsteht, obwohl die Leiter, in denen diese Ströme fließen, mit dem Rotor gedreht wer-
den.
Daher treten durch das Zusammenwirken von magnetischem Feld und Rotorströmen unter dem
Pol 1 Tangentialkräfte nach links und unter dem Pol 2 Tangentialkräfte nach rechts auf. Sie bilden
das Drehmoment der Maschine.
Die Kraft auf einen Stab, welcher den Strom I/2 führt, ist
I
F= · B · lp (2.5)
2
Die Zahl der Stäbe ist N, Kräfte treten jedoch nur an den Stäben unter den Polen auf, da nur hier
ein radiales Magnetfeld mit der magnetischen Induktion B auftritt. Die Breite eines Poles (am
Luftspalt) sei bp, dann ist der Ausdruck
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

13. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 13 von 108
bp
αp = (2.6)
π⋅r
die (relative) „Polbedeckung“. Sie soll so groß wie möglich sein, um einen großen Einfluss in der
Maschine zur Wirkung zu bringen, jedoch kann die Polbedeckung nicht gegen 1 gehen, da sonst
ein zu großer Polstreufluss (Abbildung 2.11) auftritt, der keine Wirkung auf den Rotor ausübt,
aber der durch das Eisen des magnetischen Joches fließt und es in die magnetische Sättigung trei-
ben kann. Übliche Werte für die Polbedeckung liegen zwischen 0,6 und 0,7.
Polstreufluss
Nutzfluss
Abbildung 2.11: Feldlinien, die den Anker nicht durchqueren, tragen nicht zum Drehmoment bei
Das Drehmoment der Gleichstrommaschine ergibt sich dann aus Gleichung (2.5) und (2.6):
M = N · αp · I · BL · lp · r
In dieser Gleichung ist N · αp die wirksame Leiterzahl und r der Radius des Rotors. Setzt man
Gleichung (2.6) ein, so ist:
N
M= · I · BL · lp · bp
π
Mit dem magnetischen Fluss aus Gleichung (2.2) wird das kürzer:
N
M= ·I·Φ (2.7)
π
Die Spannung der Gleichstrommaschine kann bei Vernachlässigung der Verluste in der Rotor-
wicklung durch Gleichsetzen der mechanischen und der elektrischen Leistung berechnet werden:
U·I=M·ω
(2.8)
N
U= ·ω·Φ
π
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

14. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 14 von 108
Es ist beachtenswert, dass die Gleichungen (2.7 und 2.8) für Strom und Spannung von Gleich-
strommaschinen unabhängig von den Abmessungen der Maschine sind und dass nur die Win-
dungszahl N als Faktor vorkommt. Die Abmessungen der Maschine sind natürlich indirekt rele-
vant für das größtmögliche Drehmoment, da der Maximalwert des Flusses vom Eisenquerschnitt
des Joches begrenzt ist. Auch der Maximalwert des Stromes ist über die erforderlichen Stabquer-
schnitte durch die Abmessungen des Rotors begrenzt.
2.4 Mechanische Abmessungen
Als Gedankenexperiment wird ausgehend von einer gegebenen Maschine eine größere Maschine
dadurch konstruiert, dass man alle Abmessungen um den Faktor x vergrößert. Dies wirkt sich auf
das Drehmoment der Maschine folgendermaßen aus:
Die magnetische Flussdichte ist durch die Materialeigenschaften des Eisens bestimmt, also ist der
Fluss nur durch die Fläche bestimmt:
Φ ~ x2
Der Ankerstrom ist hauptsächlich durch die abführbare Verlustleistung bestimmt. Da die maximal
zulässigen Temperaturen durch die Werkstoffe bestimmt sind, ist die an der Oberfläche der Ma-
schine abzugebende Wärme nur von der Oberfläche abhängig, also
PV ~ x2
Die Verluste im Anker machen einen großen Teil dieser Verluste aus, also
R · I2 ~ x2
Der Widerstand R nimmt mit der Länge zu und mit wachsendem Querschnitt ab, also
1
R~
x
Somit resultiert für den Ankerstrom
I2 ~ x3
und mit Gleichung (2.7) für das Moment
7
M ~ x2
Das Gewicht der Maschine ist proportional zum Volumen, also:
G ~ x3
6
G ~ M7
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

15. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 15 von 108
Es ist also zu erkennen, dass bei einer Baureihe von ähnlichen Maschinen das Gewicht etwa pro-
portional dem Nennmoment ist. Die Nenndrehzahl und somit die Nennleistung sind nicht die be-
stimmenden Größen.
⎢⎢Abmessungen und Gewicht einer Maschine sind durch Nennmoment bestimmt. ⎢⎢
2.5 Feldlinienbild, Ankerrückwirkung
Im Luftspalt der Maschine überlagert sich das Erregerfeld mit den von den stromdurchflossenen
Läuferstäben erzeugten Feldern (Abbildung 2.12). Die resultierende Feldkurve ergibt sich durch
die Überlagerung der einzelnen Feldkurven.
Feld ohne Ankerrückwirkung
Überlagerung von Erreger-
und Rotorfeld X
A B
Abbildung 2.12: Zur Feldverzerrung und Verschiebung der neutralen Zone durch Ankerrückwir-
kung
Man erkennt, dass durch den Ankerstrom eine Feldverzerrung auftritt. Die erhöhte magnetische
Flussdichte an den rechten Polkanten, an denen sich Erregerfeld und Ankerfeld addieren, führt zur
lokalen Eisensättigung und dadurch zu einer Verminderung des Erregerflusses, d. h. Drehmoment
und die induzierte Spannung sinken. Das ist die „Ankerrückwirkung“ der Gleichstrommaschine.
Bei einem Betrieb der Maschine an einer konstanten Spannungsversorgung würde nach Gleichung
(2.8) ein verminderter Fluss zu einer erhöhten Drehzahl führen müssen. Mit steigendem Drehmo-
ment würde deshalb auch die Drehzahl ansteigen.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

16. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 16 von 108
2.6 Kompensations- und Wendepolwicklungen
Die Bürsten müssen so breit sein, dass sie immer mehr als ein Kommutatorsegment überbrücken
(üblich ist eine Überdeckung von 2 bis 4,5 Segmenten). Dadurch werden Stromunterbrechungen
vermieden, aber während des Kommutierungsvorganges sind mehrere Schleifen kurzgeschlossen.
In Abbildung 2.13 ist ein Zustand dargestellt, bei dem gerade der Übergang von 1 nach 2 erfolgt.
Die dick markierte Wicklung ist dabei kurzgeschlossen. Ohne die Ankerrückwirkung (Abbildung
2.12) ist in der Pollücke das Feld = 0, eine kleine Verschiebung der kurzgeschlossenen Schleife
erzeugt somit auch keine Flussänderung und induziert keine Spannung zwischen den kurzge-
schlossenen Kommutatorsegmenten 1 und 2.
Pol1
Pol1
7 8 1 2 3 4 5 6 7
B
Abbildung 2.13: Kurzschluss einer Windung während des Kommutierungsvorganges
Die Ankerrückwirkung verdreht nun das Feld etwas, sodass die Leiter der kurzgeschlossenen
Schleife nicht mehr in dem feldfreien Bereich liegen. Dadurch wird in der kurzgeschlossenen
Schleife eine Spannung induziert. Dies erzeugt einen Strom. Wenn die Bürste A die Lamelle 1
verlässt, wird dieser Strom abrupt unterbrochen. Dies führt zu starken Funken (Feuern) und damit
zu einer Abnutzung der Bürsten. Eine lastabhängige mechanische Verdrehung der Bürsten in der
Weise, dass die jeweils kurzgeschlossenen Windungen in der feldfreien Zone liegen, behebt die-
sen Mangel. Üblich ist jedoch heute folgende magnetische Korrektur:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

17. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 17 von 108
Es werden zusätzliche „Wendepole“ in der Pollücke angeordnet, um die Wirkung der Rotorströme
zu kompensieren (Abbildung 2.14). Dazu muss ihre elektrische Durchflutung i · NW ebenso groß
sein, wie die Rotordurchflutung N · i/2.
Die Wendepole sind also für hohe Durchflutung (viel Kupfer) und nur für geringe Flüsse (kleiner
Eisenquerschnitt) auszulegen.
Der Ankerstrom erzeugt neben dem Feld entsprechend Abbildung 2.12 auch einen Streufluss in
den Nuten und um die Leiter außerhalb des Blechpaketes (Wickelköpfe). Dieser Streufluss bremst
den gleichmäßigen Übergang des Stromes während der Kommutierung und ist ebenfalls Ursache
für ein Feuern der Bürsten. Eine etwas stärkere Wendepolwicklung kann auch diesen Effekt weit-
gehend ausgleichen.
Pol 2
Nω Nω
2 2
A i
B
Pol 1
Abbildung 2.14: Die Wendepolwicklungen sind so geschaltet, dass ihr Feld dem Anker(quer)feld
entgegenwirkt
Die Feldschwächung durch Sättigung der Polkanten kann durch die Wendepole nur sehr unvoll-
kommen ausgeglichen werden. Bei großen Gleichstrommaschinen ist es deshalb wirtschaftlicher
und erfolgreicher, die Wendepolwicklung teilweise in den Hauptpolen unterzubringen (Abbildung
2.15), wodurch die Wirkung der Rotorströme am gegenüberliegenden Teil des Pols kompensiert
wird. Derartige Anordnungen werden als Kompensationswicklung bezeichnet. Auf den Wendepo-
len ist dann kein großer Wickelraum erforderlich.
Diese Maschinen werden kompensierte Gleichstrommaschinen genannt. Sie sind im Betrieb sehr
unempfindlich gegen Überlastungen und Kurzschlüsse.
Große Maschinen sind immer kompensiert, bei kleineren Maschinen wird auf die Kompensati-
onswicklung und gelegentlich auch auf eine Wendepolwicklung zu Gunsten eines niedrigen Prei-
ses verzichtet. Die Nachteile der Ankerrückwirkung können bei kleineren Maschinen leichter als
bei großen Maschinen in Kauf genommen und z. T. durch geeignete Auslegung vermindert wer-
den.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

18. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 18 von 108
i
i
B
i
Abbildung 2.15: Die Kompensationswicklung in den Polen und die Wendepolwicklung wirken
dem Anker(quer)feld entgegen
2.7 Betriebsverhalten und Kennlinien
2.7.1 Spannungsgleichung und Drehmomentgleichung
Die Gleichungen (2.7) und (2.8) können wie folgt dargestellt werden:
Ui = k1 · n · Φ (2.9)
k1
M= ·Φ·I (2.10)
2π
Ui ist die induzierte Spannung
In der Maschinenkonstante k1 sind alle Wicklungsdaten der Maschine zusammengefasst.
Aus Gleichungen (2.9) und (2.10) ist erkennbar, dass die Gleichstrommaschine sich sehr einfach
in Bezug auf Drehmoment und Drehzahl regeln lässt:
− Nach Gleichung (2.9) kann die Drehzahl sowohl über die Spannung als auch über den Fluss
beeinflusst werden.
− Nach Gleichung (2.10) ist bei gegebenem Fluss das Drehmoment proportional dem Anker-
strom.
Aus diesen Gründen wird die Gleichstrommaschine auch heute noch - trotz ihrer offensichtlichen
Nachteile in Bezug auf den Verschleiß von Bürsten und Kommutator - in einer Vielzahl von dreh-
zahl- und drehmomentgeregelten Antrieben eingesetzt.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

19. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 19 von 108
2.7.2 Fremderregung, Permanenterregung
I
U
Ie
Ue
Abbildung 2.16: Schaltung der fremderregten Gleichstrommaschine
RA
I
U Ui = k1·Φ·n
Abbildung 2.17: Ersatzschaltbild für den Ankerkreis
Alle Widerstände des Ankerkreises (Widerstände der Ankerwicklung und anderer Wicklungen
wie Wendepolwicklungen und Kompensationswicklungen (s. u.) sowie der Bürsten) sind im Er-
satzschaltbild Abbildung 2.17 im Ankerkreiswiderstand RA zusammengefasst. Im Anker wird die
Spannung Ui induziert. Die Feldwicklung wird unabhängig vom Ankerkreis mit einem Erreger-
strom Ie gespeist, der den Fluss Φ zur Folge hat. An den Ankerklemmen liegt die Spannung U.
Nach Abbildung 2.17 gilt:
U = I · RA + Ui
U = I · RA + k1 · Φ · n (2.11)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

20. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 20 von 108
Mit Gleichung (2.10) ist:
R A ⋅ 2π
U= · M + k1 · Φ · n
k1 ⋅ Φ
U R A ⋅ 2π
n= - ·M (2.12)
k 1 ⋅ Φ (k 1 ⋅ Φ ) 2
n Grenzen für
2 0
Feldschwächung
Feldstellbereich
1
φ = φ n ,U =U n
2
n0 φ =φ n ,U =U n
I
I 1
1 φ =φ n ,U = U n
n 2
2 0
Generator Mo-
II Mn M
I
Motor Generator Ankerstellbereich
Abbildung 2.18: Kennlinien der fremderregten Gleichstrommaschine
Index n: Nennwerte
no: Leerlaufdrehzahl
Aus Gleichung (2.12) ergibt sich, dass im Betriebsbereich mit vollem Feld die Drehzahl-
Drehmoment-Kennlinien parallele Geraden sind. Im Feldschwächbereich bei konstanter Anker-
spannung ändert sich die Neigung dieser Kennlinien, die Drehzahlverringerung der Maschine bei
Belastung wird größer, die Maschine wird „weicher“.
Un
Die Nennleerlaufdrehzahl ist no = (2.13)
k1 ⋅ Φ n
Diese Drehzahl wird auch als die natürliche Drehzahl bezeichnet.
Würde im Leerlauffall die Erregung abgeschaltet (Φ = 0), so würde die Drehzahl nur durch Rei-
bung begrenzt und unzulässig hohe Werte annehmen („Durchgehen“ der Gleichstrommaschine!).
Wie in Abbildung 2.18 ersichtlich, kann die Drehzahl durch „Feldschwächung“ (Verringerung
von Φ) über die Leerlaufdrehzahl hinaus auch unter Last angehoben werden. Im Dauerbetrieb darf
der Ankerstrom aus Erwärmungsgründen seinen Nennwert nicht überschreiten. Ersetzt man Φ in
Gleichung (2.12) mit Gleichung (2.10) durch
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

21. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 21 von 108
2π M
Φ=
k1 ⋅ I n
so erhält man die zulässige Drehzahl im Feldschwächbereich:
U N ⋅ In R A ⋅ In
2
nZul = − (2.14)
2π M 2π M
Die zulässige Drehzahl im Feldschwächbereich ist also umgekehrt proportional zum Drehmoment.
1
nZul ∼
M
Dieser Zusammenhang wird durch eine Hyperbel dargestellt. Sie ist in Abbildung 2.18 mit einge-
tragen.
Der zulässigen Drehzahlerhöhung ist außerdem, abhängig von der Auslegung der Maschine, eine
obere Grenze gesetzt (Fliehkräfte, Kommutierung).
Treibt man die Maschine an (M < 0), so wird Ui > U, die Stromflussrichtung kehrt sich um und die
Maschine wird zum Generator (II. Quadrant). Für den Betrieb mit umgekehrter Drehrichtung (III.
und IV. Quadrant) ist die Feldwicklung umzupolen.
Man unterscheidet bei der fremderregten Gleichstrommaschine also einen „Ankerstellbereich“, in
dem die Drehzahl durch Variation der Ankerkreisspannung U eingestellt wird und einen „Feld-
stellbereich“, in dem der Ankerkreis an der Nennspannung Un liegt und die Erregung Φ ge-
schwächt wird.
Die variable Ankerkreisspannung wird heute i. a. aus dem Drehstromnetz mit Hilfe von Strom-
richtern erzeugt.
Eine andere auch heute noch manchmal verwendete Methode der Drehzahlsteuerung z. B. von
Prüfständen besteht in der Erzeugung der variablen Ankerspannung durch einen Gleichstromgene-
rator, der von einem Drehstrom-Asynchronmotor mit etwa konstanter Drehzahl angetrieben wird
(Leonard-Satz):
3~
φG φM
ASM G M
Abbildung 2.19: Schaltung des Leonard-Satzes
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

22. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 22 von 108
Die Ankerspannung des Motors wird über den variablen Fluss Φ G des Gleichstromgenerators
eingestellt. Durch entsprechende Beträge und Polaritäten der Flüsse sowie Feldschwächung des
Motors kann das Kennlinienfeld gemäß Abbildung 2.18 erzeugt werden.
Bei kleinen Motoren wird die Feldwicklung eingespart, stattdessen sind die Pole des Ständers aus
einem Permanentmagneten hergestellt. Das Betriebsverhalten entspricht einer fremderregten Ma-
schine, wobei ein Feldschwächbereich natürlich nicht möglich ist.
Bei Antrieben, die keine Drehzahlverstellung erfordern, kann die Erregerwicklung aus der glei-
chen Quelle wie der Anker versorgt werden. Die Erregerwicklung ist dann einfach parallel zum
Anker geschaltet. Diese Variante wird als Nebenschluss-Motor bezeichnet.
2.7.3 Reihenschlussverhalten
U Ui Φ
RF
RSh
Abbildung 2.20: Schaltung der Gleichstrom-Reihenschlussmaschine
Die Erregerwicklung ist hier in Reihe mit dem Anker geschaltet, RF bildet den ohmschen Wider-
stand der Wicklung ab.
Für die ungesättigte Maschine ist:
Φ∼I
Φ = k3 · I
Ui = k1 · k3 · n · I (2.15)
k1
M= · k3 · I2 (2.16)
2π
Unter Einbeziehung des Widerstandes RF der Erregerwicklung ergibt sich die Gleichung für die
Klemmenspannung:
U = (RA + RF) · I + k1 · k3 · n · I (2.17)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

23. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 23 von 108
Einsetzen der Gleichung (2.16) und weitere Umformung führt auf die Drehzahl-Drehmoment-
Gleichung der Reihenschlussmaschine:
1 U R + RF
n= · - A (2.18)
2 πk 1 k 3 M k1k 3
Abbildung 2.21 zeigt das Kennlinienfeld der Reihenschlussmaschine.
Eine Feldschwächung kann dadurch erreicht werden, dass man einen Nebenwiderstand (Shunt)
RSH parallel zur Erregerwicklung schaltet und dadurch nicht den vollen Ankerstrom zur Felderre-
gung nutzt.
n
U = Un
Feldschwächung durch RSh
U = Un
1
U= Un
2
M
Abbildung 2.21: Kennlinien des Reihenschlussmotors
Wegen ihrer besonderen Drehzahl-Drehmoment-Charakteristik (hohes Drehmoment bei niedriger
Drehzahl und niedriges Drehmoment bei hoher Drehzahl) ist die Gleichstrom-Reihenschlussma-
schine besonders für Antriebe von Fahrzeugen (U-Bahn, Straßenbahn, Hubstaplern) geeignet. Die
Spannung und damit die Drehzahl wird hierbei durch Vorwiderstände, Reihen-Parallelschaltungen
von Motoren oder elektronische Gleichstromsteller eingestellt. Heute wird in diesen Anwendun-
gen jedoch meistens ein Drehstrommotor mit einem elektronischen Wechselrichter eingesetzt.
Ein „Durchgehen“ bei vollständiger Entlastung ist gemäß Gleichung (2.18) beim Reihenschluss-
motor ebenfalls möglich; bei den oben genannten Hauptanwendungsgebieten des Reihenschluss-
motors tritt eine vollständige Entlastung allerdings in der Praxis nicht auf.
Das Drehmoment kann nach Gleichung (2.16) nur positiv sein. Ein Betrieb als Generator ist des-
halb nur für n < 0 möglich. Die aus Gleichungen (2.15 – 2.18) resultierenden Betriebskennlinien
sind aber nur für Sonderfälle brauchbar. Mit einer zusätzlichen fremderregten Wicklung entsteht
eine Mischform von Nebenschluss- und Reihenschlussmaschine, die auch als Generator gut ge-
eignet ist und früher viel eingesetzt wurde. Je nach Gewichtung der Reihenschlusswicklung und
fremderregten Wicklung können Betriebskennlinien als Überlagerung der Diagramme Abbildung
2.18 und Abbildung 2.21 erreicht werden.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

24. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 24 von 108
2.7.4 Wechselstrommotoren
Der Reihenschlussmotor ändert seine Drehrichtung nicht, wenn sich die Stromrichtung umkehrt,
da sich Feld und Ankerstrom jeweils gleichsinnig ändern. Deshalb kann ein Reihenschlussmotor
prinzipiell auch mit Wechselstrom betrieben werden. (Es gibt sogar Bauarten für Drehstrom.) Der
Ständer muss dafür natürlich aus Blechen aufgebaut sein. Da bei Wechselstrom die Induktivitäten
aller Wicklungen eine wesentliche Rolle spielen, ist eine andere Dimensionierung als bei Gleich-
strom nötig. Antriebe in Haushaltsmaschinen und Heimwerker-Werkzeugen sind oft Motoren die-
ser Art.
Mit Kompromissen gelingt es, eine Auslegung zu finden, die sowohl für Gleichstrom als auch für
Wechselstrom ein brauchbares Betriebsverhalten ergibt (Universalmotoren).
Nebenschlussmotoren sind im Prinzip auch für Wechselspannung geeignet. Da in der Erreger-
wicklung der Strom jedoch um 90° phasenverschoben gegenüber der Spannung ist, der Anker-
strom jedoch auch einen Wirkstrom beinhaltet, sind Ankerstrom und Feld nicht in Phase und das
Drehmoment hat wechselnde Vorzeichen.
3 Drehfeldmaschinen
3.1 Drehfelder in elektrischen Maschinen, Drehmoment und Abmessungen
3.1.1 Zum Aufbau von Drehfeldmaschinen
Drehfelder sind die Basis für die Arbeitsweise verschiedener Drehstrommaschinen (Asynchron-
motoren, Synchrongeneratoren u. a.). Der feststehende Teil dieser Maschinen wird als Stator (bei
Asynchronmaschinen auch als Ständer) bezeichnet. Der Stator ist ein aus Eisenblechen aufgebau-
ter Ringzylinder. An der Innenfläche befinden sich Nuten, in denen eine Wicklung aus Kupfer-
draht oder –stäben untergebracht ist. Die Wicklung schließt sich an den Stirnseiten des Zylinders
(Wickelköpfe).
Der rotierende Teil (Rotor, Läufer) ist für die verschiedenartigen Maschinen unterschiedlich auf-
gebaut. Für die folgende Betrachtung der Entstehung des Drehfeldes wird am Einfachsten vom
Läufer einer Asynchronmaschine ausgegangen. Dieser ist ein aus Eisenblechen aufgebauter Zylin-
der, in dessen äußerem Mantel in Nuten eine Wicklung eingebracht ist, die aber im Folgenden
keine Rolle spielt. Zwischen dem rotierenden Teil und dem feststehenden Teil befindet sich der
Luftspalt, der je nach Maschinenart etwa 1 – 10 mm weit ist. In jedem Fall ist der Luftspalt so eng,
dass bei der Betrachtung der magnetischen Verhältnisse zwischen dem Innenradius des Stators
und dem Radius des Rotors nicht unterschieden werden muss; man rechnet ggf. mit einem mittle-
ren Radius. Abbildung 3.1 zeigt den gesamten Aufbau. Die Koordinate x sei der Winkel.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

25. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 25 von 108
iR
7 6
8 5
x
9 4
Stator Rotor
10 3
11 2
12 1
Stabverbindung iR
auf der Rückseite
Abbildung 3.1: Beispiel einer Drehfeldmaschine mit Drehstromwicklung in zwölf Statornuten
(nur die Stäbe des Stranges R sind gezeichnet).
3.1.2 Grundprinzip der Drehfeldbildung
Drehstromwicklung
x 2 /p
ic Schließt man die drei um räumlich 120° gegeneinander
versetzten Wicklungsstränge an ein symmetrisches Dreh-
ia stromsystem an, dann wandert das Maximum des Stromes
wie eine Welle dem Luftspalt entlang.
ib Nimmt die dargestellte Anordnung nur 180° des (räumli-
chen) Umfanges ein und wiederholt sich dann, dann legt
Drehfeld das Maximum während einer Netzperiode nur 180° zurück.
ia ib ic
Die Anzahl der Wiederholungen am Umfang wird als Pol-
t=0 paarzahl p bezeichnet. Man bezeichnet den Winkel γ = p ⋅ x
als elektrischen Winkel.
t = 1/6
t = 1/3
t = 1/2 Abbildung 3.2: Zur Bildung des Drehfeldes
t = 2/3
Feld = /p
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

26. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 26 von 108
3.1.3 Beschreibung des Drehfeldes
Abbildung 3.3 zeigt eine Abwicklung des Luftspaltes der Anordnung in Abbildung 3.1.
Stator
4 5 6 7 8 9 10 11 12 1 2 3
δ H(0) H(x)
2π x
Rotor
H,B
Abbildung 3.3: Zur Ermittlung des Feldverlaufes
Die durch den Strom i erzeugte magnetische Feldstärke wird aus dem Durchflutungssatz ermittelt:
x
H(0) ⋅ δ - H(x) ⋅ δ = ∑i
x=o
(3.1)
und B = µo ⋅ H.
Berücksichtigt man als Randbedingung, dass H(x) den Mittelwert 0 haben muss, dann ergibt sich
der in Abbildung 3.3 dargestellte Feldverlauf. Charakteristisch sind die Sprungstellen an den
stromdurchflossenen (als schmal angenommenen) Nuten. Die Feldform hängt also stark davon ab,
wie viele Nuten es gibt und wie die Wicklung in den Nuten verteilt ist.
Für die weitere Betrachtung und die Überlagerung der Felder der Ströme in allen drei Wicklungs-
strängen ist die Fourier-Zerlegung gut geeignet. Die durch den Strom iR erzeugte Flussdichte in
Abbildung 3.3 kann also geschrieben werden:
∞
bR(γ) = B R ⋅ ∑ C i ⋅ sin(i ⋅ γ )
i =1
mit γ = p ⋅ x, um auch den Fall höherer Polpaarzahlen berücksichtigen zu können. (Eine mögliche
Phasenverschiebung spielt für das Folgende keine Rolle und ist deshalb weggelassen.) Ci kann nur
ungerade sein, das wird hier aber nicht berücksichtigt. Der (räumliche) Scheitelwert B R ist pro-
portional zum Strom iR, also bei willkürlicher Wahl des zeitlichen Bezugspunktes:
B R = B ⋅ sin(ω ⋅ t )
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

27. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 27 von 108
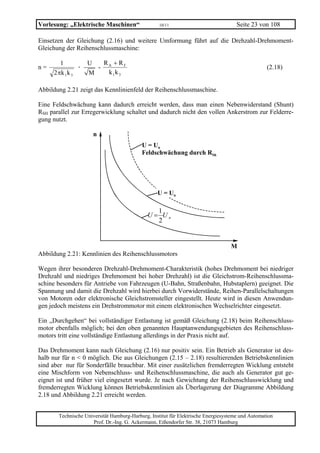
Für die Wicklungsstränge S und T muss jeweils die räumliche und zeitliche Verschiebung um
± 120° (± 2/3 π) ergänzt werden und man erhält:
∞
bR(γ,t) = B ⋅ sin (ω ⋅ t) ⋅ ∑C
i =1
i ⋅ sin (i ⋅ γ)
∞
2 2
bS (γ, t) = B ⋅ sin (ω ⋅ t -
3
π) ⋅ ∑C
i =1
i ⋅ sin (i ⋅ γ -
3
π)
∞
2 2
bT (γ,t) = B ⋅ sin (ω ⋅ t +
3
π) ⋅ ∑C
i =1
i ⋅ sin (i ⋅ γ +
3
π)
1
Unter Nutzung der Gleichung (Additionstheorem) sin α ⋅ sin β = [cos (α - β) - cos (α + β)] und
2
von
4 2
cos (x - π) = cos (x + π) folgt:
3 3
∞
B
bR (γ, t) =
2
⋅ ∑C
i =1
i [cos (ωt – i ⋅ γ) - cos (ω ⋅ t + i ⋅ γ)]
∞
B 2
bS (γ, t) =
2
⋅ ∑C
i =1
i [cos (ωt – i ⋅ γ) – cos (ω ⋅ t + i ⋅ γ +
3
π)]
∞
B 2
bT (γ, t) =
2
⋅ ∑C
i =1
i [cos (ωt – i ⋅ γ) – cos (ω ⋅ t + i ⋅ γ -
3
π)]
Das gesamte Feld ist die Addition der drei einzelnen Felder. Da die Summe der zweiten cos-
Terme null ist, folgt schließlich:
∞
3
b (γ, t) =
2
B ⋅ ∑C i =1
i ⋅ cos (ω ⋅ t – i ⋅ γ)
∞
3
b (γ, t) =
2
B ⋅ ∑C i =1
i ⋅ cos (ω ⋅ t – i ⋅ p ⋅ x)
Das gesamte Feld besteht also aus :
1. Grundfeld (i = 1), das die Polpaarzahl p besitzt und mit der Winkelgeschwindigkeit
ωo = ω/p (synchrone Drehzahl) rotiert (s. auch Abbildung 3.9).
2. Oberfelder (i > 1), die die Polpaarzahl i ⋅ p besitzen und entsprechend mit
ωi = ωo/(i⋅p) rotieren.
Die Drehzahl des Rotors in einer Drehfeldmaschine ist durch das Grundfeld bestimmt (synchron
oder asynchron). Die Oberfelder würden eine Rotation mit 1/3, 1/5 ... Drehzahl erzeugen wollen
und würden so die eigentliche Funktion behindern.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

28. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 28 von 108
Die Oberfelder müssen also möglichst vermieden werden. (In Ergänzung wird auch die Wicklung
im Rotor möglichst so gestaltet, dass sie auf ggf. verbleibende Oberfelder möglichst nicht rea-
giert). Es ist also anzustreben, das Ci = 0 für i > 1 ist.
Jeder Strang muss also ein möglichst sinusförmiges Feld erzeugen. Entsprechend der Darstellung
in Abbildung 3.3 müssen die Windungen jeden Stranges deshalb auf mehrere Nuten verteilt wer-
den. Bereits mit der Aufteilung auf je zwei Nuten wie in Abbildung 3.1 und 3.3 ist einiges er-
reicht, wie Abbildung 3.4 zeigt.
Eine weitere Verbesserung lässt sich erzielen, wenn sich die Bereiche der einzelnen Wicklungs-
stränge überlappen, es also Nuten gibt, in der Wicklungen aus verschiedenen Strängen liegen. Die
Möglichkeit einer wirtschaftlichen Fertigung der Wicklung hat außerdem einen wesentlichen Ein-
fluss auf die Gestaltung.
B
t=0
1 2 3 4 5 6 7 8 9 10 11 12
T
t=
4
1 2 3 4 5 6 7 8 9 10 11 12
Abbildung 3.4: Feldverlauf bei zwei Nuten pro Pol und Strang
Abbildung 3.5 zeigt die Wicklung und den resultierenden Feldverlauf für einen gebauten 510 kW-
Drehstromasynchronmotor für zwei verschiedene Zeitpunkte zusammen mit einer ideal sinusför-
migen Kurve. Die Wicklung liegt in zwei Schichten in den Nuten, sie wird deshalb als Zwei-
schichtwicklung bezeichnet. Dies ist heute eine übliche Bauart. Man erkennt, dass so die Sinus-
form schon sehr gut angenähert ist.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

29. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 29 von 108
Nutnr. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
Strang m. +R +R +R +R +R +R -T -T -T -T -T -T +S +S +S +S +S +S -R -R -R -R -R -R +T +T +T +T +T +T -S -S -S -S -S -S
Richtung +R +R +R -T -T -T -T -T -T +S +S +S +S +S +S -R -R -R -R -R -R +T +T +T +T +T +T -S -S -S -S -S -S +R +R +R
Durchflutung 510 kW DASM
2,5
2
1,5
1
0,5
0
1 10 19 28 37 46 55 64
-0,5
-1
-1,5
-2
-2,5
Nutnr.
Abbildung 3.5: Wicklungsanordnung und Feldverlauf für zwei verschiedene Zeitpunkte
3.1.4 Drehmoment, Strombelag, Abmessungen
Nützlich ist ein Bezug des Stromes auf die Länge in Umfangsrichtung. Der Quotient
1 dΘ 1 dΣi
AS = ⋅ = ⋅
r dx r dx
wird als Strombelag bezeichnet. Bei üblichen Maschinen ist etwa AS = 1000 A/cm. Aus Gleichung
3.1 kann dann der Zusammenhang
dH(x) r
= − · AS(x)
dx δ
entnommen werden.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

30. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 30 von 108
Setzt man in folgende Gleichung für die Kraft auf einen stromdurchflossenen Leiter
F=l·B·I
statt des Stromes den Strombelag ein, dann erhält man mit
σ = B · AS
die Kraft pro Fläche am Umfang, dies wird Drehschub genannt.
Die magnetische Flussdichte B ist bei Drehfeldmaschinen am Maschinenumfang annähernd sinus-
ˆ ˆ
förmig verteilt, sie liegt zwischen B und - B . Der Strombelag AS ist ebenfalls am Maschinenum-
ˆ ˆ
fang annähernd sinusförmig verteilt und nimmt Werte zwischen AS und - AS an. Wenn am Um-
fang Feldstärke und Strombelag ihr Maximum am gleichen Ort hätten, schwankt der Drehschub
am Umfang zwischen null und einem Maximalwert (die Maschine hätte einen Leistungsfaktor cos
ϕ = 1).
A,B,σ
σ
A
B
X
Abbildung 3.6: Feld, Strombelag und Schub in einer Drehfeldmaschine (cos ϕ = 1)
Der „mittlere Drehschub σ “ ist dafür
1 1 ˆ ˆ
σ= σ=
ˆ ⋅ AS ⋅ B
2 2
Bei den üblichen Werten B = 1 T und AS = 1.000 A/cm ist σ = 5 N/cm2.
ˆ ˆ
Es muss beachtet werden, dass die magnetische Feldstärke B meistens als Scheitelwert angegeben
wird, der Strom, aus dem AS berechnet wird, ist meistens als Effektivwert angegeben.
Zu den Abmessungen einer Maschine gelten sinngemäß die gleichen Überlegungen wie für die
Gleichstrommaschine in Kapitel 2.4 und führen zu dem gleichen Ergebnis:
Die Größe einer Maschine wird also eher durch das Drehmoment und weniger durch die
Leistung bestimmt!
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

31. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 31 von 108
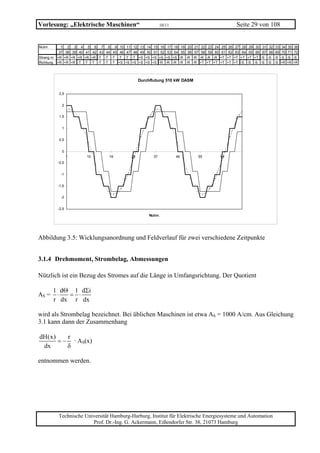
Die folgenden Diagramme zeigen diesen Zusammenhang für eine handelsübliche Baureihe von
Asynchronmotoren.
2500
2000
Masse [kg]
1500
3600 1/min
1000
1800 1/min
1200 1/min
500
900 1/min
0
0 0,5 1 1,5 2 2,5 3
Drehmoment [kN]
2500
2000
Masse [kg]
1500
3600 1/min
1000 1800 1/min
1200 1/min
500 900 1/min
0
0 50 100 150 200 250 300 350 400 450
Leistung [kW]
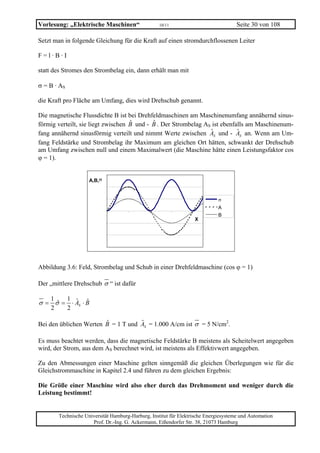
Abbildung 3.7: Zusammenhang zwischen Baugröße (hier die Masse), Drehmoment und Leistung
für eine Baureihe von Drehstromasynchronmaschinen mit Käfigläufer
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

32. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 32 von 108
3.2 Asynchronmaschinen
3.2.1 Besondere Formelzeichen und Begriffe
Strang:
Eine Wicklung der Maschine (ggf. aus mehreren Teilen bestehend), die zwischen zwei Leiter des
Netzes oder zwischen einem Leiter und einem Sternpunkt geschaltet ist.
Index:
0: Leerlauf
1: Stator, Ständer
2: Rotor, Läufer
3.2.2 Aufbau der Ständer- und Läuferwicklung, Begriffe
Asynchronmotoren sind die in der industriellen Antriebstechnik und in Bordnetzen von Schiffen
am häufigsten vorkommenden Maschinen. Der Stator eines Asynchronmotors (oft auch Ständer
genannt) ist aus Blechringen zu einem Ringzylinder zusammengeschichtet. Am inneren Umfang
befinden sich in Nuten der drei Drehstromwicklungen. Bei kleineren Maschinen besteht diese aus
isoliertem Kupferdraht, bei größeren Maschinen aus isolierten Kupferstäben. Die Stäbe sind an
den Stirnseiten durch Verbindungen zu geschlossenen Wicklungen zusammengeschaltet. Die drei
Wicklungsstränge sind in Sternschaltung oder in Dreieckschaltung mit dem speisenden Netz ver-
bunden.
V
U
V
W
U Φh
Φσ1
U
V
W
W
Abbildung 3.8: Alternative Schaltungen von Drehstromwicklungen
Die drei Stränge sind über den Umfang um je 120° versetzt angeordnet, die Rückleiter eines jeden
Stranges liegen also den zugehörigen Hinleitern genau gegenüber. Hin- und Rückleiter liegen also
um 180° auseinander.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

33. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 33 von 108
ω0 ω0/2
Abbildung 3.9: Drehfeld mit Polpaarzahl 1 (links) und 2 (rechts)
Beim Anschluss des Stators an ein Drehstromsystem entsteht im Luftspalt ein magnetisches Feld,
welches längs des Luftspaltumfanges annähernd sinusförmig verteilt ist. Diese Feldstärkewelle
läuft mit konstanter, nur von der Netzfrequenz abhängiger Geschwindigkeit um.
Macht man jeden Strang nur 180°/p (p = ganze Zahl) groß, versetzt die drei Stränge nur um 120°/p
gegeneinander und wiederholt diese Anordnung p-mal über den Umfang, dann wiederholt sich
auch das Feldbild p-mal. p wird als die Polpaarzahl bezeichnet. (In Abbildung 3.9 ist das Feldbild
für p = 1 und für p = 2 dargestellt).
In der Bohrung des Stators ist der Rotor angeordnet, der ebenfalls aus Einzelblechen zusammen-
geschichtet ist. Die Wicklungen des Rotors bestehen aus Stäben, die Stäbe sind an den Stirnseiten
durch Verbindungen zu geschlossenen Wicklungen zusammengeschaltet. Die Rotorwicklungen
einer Asynchronmaschine sind entweder kurzgeschlossen oder die Anschlüsse sind an drei
Schleifringe angeschlossen, über die sie über Kohlebürsten elektrisch zugänglich sind.
Die kurzgeschlossenen Wicklungen im Rotor versuchen den Fluss möglichst fest zu halten, des-
wegen wird der Rotor von dem umlaufenden Feld mitgenommen. Bei Asynchronmaschinen wird
der Rotor auch als Läufer bezeichnet.
Es werden zunächst die Verhältnisse untersucht für einen Rotor, der nur eine in sich kurzgeschlos-
sene Spule trägt.
3.2.3 Läuferspannungsgleichung
Die im Luftspalt umlaufende magnetische Feldwelle soll durch einen umlaufenden Vektor B dar-
gestellt werden (Abbildung 3.10). Dieser Vektor zeigt in die Richtung der positiven Feldstärke-
amplitude, seine Größe ist dem Scheitelwert der umlaufenden Feldwelle proportional.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

34. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 34 von 108
Zur besseren Übersicht sind alle Darstellungen für p = 1 gemacht, die Gleichungen enthalten im-
mer auch die Polpaarzahl p.
Bei der Netzfrequenz ωN dreht B sich wie die Feldwelle mit konstanter Winkelgeschwindigkeit.
B
X
β
α
Φσ
Abbildung 3.10: Geometrische Beziehungen zwischen Magnetfeld und Läuferspule
ωo=ωN/p
Diese Drehzahl wird als Leerlaufdrehzahl oder synchrone Drehzahl bezeichnet.
β = ω0 · t
Die Spule dreht sich mit der konstanten Winkelgeschwindigkeit ω, dann ist der mechanische Win-
kel
α=ω·t
Der Fluss durch die Spulenfläche ist
Φ = Φ · sin (β - α) ⋅ p
ˆ
Φ = Φ · sin (ωN - ω ⋅ p) ⋅ t
ˆ (3.2)
Der Maximalwert des Flusses Φ geht durch die Spulenfläche, wenn (β - α) ⋅ p = π/2 ist. Die Fre-
ˆ
quenz der Ströme im Rotor ist gleich der Differenz zwischen Drehfelddrehzahl ω0 und Rotordreh-
zahl ω. Diese Drehzahldifferenz - bezogen auf die synchrone Drehzahl ω0 - wird Schlupf genannt:
ωo − ω
s= (3.3)
ω0
s = 1 tritt bei ω = 0 auf: der Rotor steht (Anlauf)
s = 0 tritt bei ω = ω0 auf: der Rotor läuft ebenso schnell wie das Drehfeld, also mit Synchron-
drehzahl
Der Fluss durch die Spulenfläche kann damit abhängig vom Schlupf ausgedrückt werden:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

35. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 35 von 108
Φ = Φ · sin (s · ωN · t)
ˆ
Die in der Spule induzierte Spannung ist (ohne Berücksichtigung des Vorzeichens)
dΦ
ui2 = = s · ωN · Φ · cos (s · ωN · t)
ˆ (3.4)
dt
Da die Spule kurzgeschlossen ist, treibt die Spannung ui2 einen Strom i2 durch den Widerstand R2
und die Streuinduktivität Lσ2 der Spule. Die Streuinduktivität ergibt sich u. a. daraus, dass der
Strom i2 auch zusätzlich ein magnetisches Feld z. B. um die stirnseitigen Kurzschlussringe und in
den Läufernuten erzeugt. Diese Felder sind ja in Φ nicht berücksichtigt.
di
ui2 = i2 R2 + Lσ2 2 (3.5)
dt
Wendet man auf Gleichung (3.3) und (3.5) die komplexe Transformation an, so wird
Ui2 = j s ωN Φ
ˆ ˆ
oder in Effektivwerten statt der Scheitelwerte
Ui2 = I2 · R2 + j s ωN I2 · Lσ2 (3.6)
(Hierbei ist zu beachten, dass die Kreisfrequenz des Stromes I2 gleich s · ωN ist, denn die treiben-
de Spannung Ui2 hat nach Gleichung (3.4) die Kreisfrequenz s ⋅ ωN.)
Daraus ergibt sich der Strom in der kurzgeschlossenen Spule
j s ωN Φ
I2 =
R 2 + j s ωN L σ2
j ωN Φ
I2 = (3.7)
R 2 / s + j ωN L σ2
Betrachtet man die Reihenschaltung eines Widerstandes R und einer Induktivität L an einer Wech-
selspannungsquelle mit der Spannung u = U cos ωN t, so ist:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

36. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 36 von 108
L
I
R
U
Abbildung 3.11: Reihenschaltung L-R passt zu Gleichung (3.8)
di
u=L +R·i
dt
U = j ωN L I + R · I
U
I= (3.8)
R + j ωN L
Die Gleichung (3.7) wird also durch die Ersatzschaltung nach Abbildung 3.11 abgebildet, wenn
L = Lσ2; R = R2/s und U = j ωN Φ
ist.
Durch Vergleich von Gleichung (3.8) mit Gleichung (3.7) ergibt sich ein Ersatzschaltbild für die
im Drehfeld rotierende kurzgeschlossene Spule:
L σ2
i2E
R2
s
^
u2E=ωNφcosωNt
Abbildung 3.12: Ersatzschaltbild für den Läuferkreis
j ωN Φ
I2E = (E: Ersatzstrom, Ersatzspannung) (3.9)
R 2 / s + j ωN L σ2
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

37. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 37 von 108
Der Strom I2E hat dabei Netzfrequenz, die Spannung U2E bzw. u2E hat ebenfalls Netzfrequenz!!
u2E = ωN Φ cos ωN t
ˆ (3.10)
U2E = j ωN Φ
In der Ersatzschaltung nach Abbildung 3.12 fließt ein Strom mit Netzfrequenz ωN, dessen Ampli-
tude und Phasenlage gegenüber der treibenden Spannung ebenso ist, wie Amplitude und Phasen-
lage des Stromes mit Schlupffrequenz sωN in der kurzgeschlossenen Rotorspule.
3.2.4 Ortskurve des Läuferstromes, Ersatzschaltbilder
Zeichnet man die Ströme I2 als komplexe Zahlen für verschiedene Werte des Schlupfes s auf, so
ergibt sich eine „Ortskurve“ nach Abbildung 3.13:
s= s=1 s=0 s=1
8
R2
ωNLσ + jωNLσ I 2E
s
s=0 s=
8
^
φ
Lσ
Abbildung 3.13: Ortskurve des Nenners von Gleichung (3.9), links,
Ortskurve des Stromes nach Gleichung (3.9), rechts
Die praktisch vorkommenden Betriebspunkte liegen zwischen s = 0 (Leerlauf) und s = 1 (Still-
stand des Rotors).
Das Drehfeld wird durch Ströme in Spulen des Stators erzeugt. Es ist zweckmäßig, davon auszu-
gehen, dass die drei Stränge der Maschine in Y geschaltet sind. Betrachtet man nun einen dieser
drei Stränge und teilt den gesamten magnetischen Fluss in einen Hauptfluss durch den Luftspalt
der Maschine und einen Streufluss in den Wickelköpfen und den Nuten auf, dann kann man diesen
Strang durch ein Ersatzschaltbild (Abbildung 3.14) nachbilden. Lh ist dabei die mit dem Haupt-
fluss verbundene Hauptinduktivität, Lσ1 ist die Streuinduktivität des Stators.
L σ1
I1
U1 Lh
Uind1 = U2E
Abbildung 3.14: Ersatzschaltbild für die Ständerwicklung
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

38. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 38 von 108
Betrachtet man eine der Statorspulen, so ist die durch das Drehfeld in ihr induzierte Spannung
dΦ
ui1 = = ωN Φ cos ωNt
ˆ (3.11)
dt
Diese Spannung ist nach Gleichung (3.10) gerade gleich der Spannung U2E, die zur Speisung der
Ersatzschaltung nach Abbildung 3.12 nötig ist.
Man kann jetzt das Ersatzschaltbild der rotierenden Spule an das Ersatzschaltbild der Statorspule
anschließen, da am Ausgang von Abbildung 3.14 und am Eingang von Abbildung 3.12 Spannun-
gen gleicher Größe und gleicher Frequenz liegen und sich das gesamte magnetische Feld im Luft-
spalt aus der Summe aus Ständerstrom und Läuferstrom ergibt.
I1 L σ1 L σ2
Lh R2
s
U1
Abbildung 3.15: Mögliches einphasiges Ersatzschaltbild
Dieses Ersatzschaltbild kann weiter vereinfacht werden: Man kann mit Hilfe der Maschen- und
Knotengleichungen zeigen, dass es keine Möglichkeit gibt, durch Messungen von U1 und I1 bei
beliebigen Werten von I1 eine Schaltung nach Abbildung 3.15 von der von Abbildung 3.16 zu
unterscheiden (die Werte für R2 unterscheiden sich aber geringfügig).
Man kann also die Hauptinduktivität Lh durch die „Leerlaufinduktivität Lo“ ersetzen, welche an
die Eingangsklemmen angeschlossen wird. Zur Berücksichtigung unterschiedlicher Windungszah-
len (und ggf. anderer Faktoren) werden Strom, Widerstand und Streuinduktivität der Rotorwick-
lungen ähnlich wie beim Transformator auf die Statorseite transformiert, deshalb ist es üblich, die
Größen mit einem Strich zu markieren. Die Größe U1 ist die Spannung an einer der drei in Y ge-
schalteten Stränge, I1 ist der Strom in einer Zuleitung.
Für die gesamte Maschine aus drei Strängen gelten insgesamt die gleichen Überlegungen. Bei
stationären Zuständen sind die Größen in allen drei Strängen aber bis auf eine Phasenverschiebung
von 120° gleich, deshalb reicht die Betrachtung eines Stranges für ein einzelnes Ersatzschaltbild
aus. Für die Berechnung transienter Vorgänge ist das einphasige Ersatzschaltbild nicht geeignet.
Bei realen Maschinen hat auch die Statorwicklung einen ohmschen Widerstand und es entstehen
auch Verluste im Eisenkern. Auf die Stromaufnahme und das Drehmoment haben diese beiden
Effekte bei Maschinen ab wenigen kW Nennleistung keinen merklichen Einfluss. Sie werden des-
halb im Ersatzschaltbild üblicherweise nicht berücksichtigt.
Im Leerlauf, für s = 0 fließt wegen R’2/s → ∞ kein Strom über L’σ und die Stromaufnahme des
Asynchronmotors ist durch die Leerlaufinduktivität Lo gegeben.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

39. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 39 von 108
L'σ
I1 I'2
I0 L’σ ≈ Lσ1 + L’σ2
R'2
L0 s Lo = Lσ1 + Lh
U1
Abbildung 3.16: Übliches einphasiges Ersatzschaltbild, gesamte Streuung in den Läufer verlegt
Die Gleichungen zu Abbildung 3.16 sind:
U1 = j ωN Lσ` I2` + R’2/s` I2`
U1
I1 = I2` + Io = I2` +
j ωN L o
⎛ 1 1 ⎞
I1 = U1 ⎜
⎜ R ' / s + jω L ' + j ω L ⎟
⎟ (3.12)
⎝ 2 N σ N 0 ⎠
3.2.5 Stromortskurve der Asynchronmaschine (Heyland-Kreis)
Mit diesen Gleichungen kann man den Statorstrom und den Rotorstrom einer ASM für jeden
Schlupf (d. h. für jede Drehzahl) berechnen und als komplexe Zahl darstellen. Es ergibt sich eine
Ortskurve mit dem Schlupf als Parameter. Legt man den Spannungszeiger U1 so, dass er nach o-
ben zeigt, und mit der reellen Achse zusammenfällt, so entsteht das Kreisdiagramm der Asyn-
chronmaschine.
Gegenüber Abbildung 3.13 ist nur der induktive Strom I0 hinzugekommen.
PK
U1
Pn
PK
IK s=1
I1n
I2n s=2
IKP
s=∞
I0 P0 IKQ P∞
s=0
s<0
Abbildung 3.17: Ortskurve des Ständerstromes (Heyland-Kreis)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

40. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 40 von 108
Die Ortskurve ergibt immer einen Kreis, sofern die Streuinduktivität L’σ unabhängig vom Schlupf
s ist, und keine Sättigung der magnetischen Kreise vom Hauptfluss und Streuflüssen auftritt.
Im Kipppunkt gibt die Maschine das maximal mögliche Moment, das Kippmoment, ab.
Der Durchmesser des Ortskurvenkreises ist U1/(ωN · Lσ`).
Der vom Motor aufgenommene Wirkstrom I1P liegt in Phase mit der Spannung U1, er ist daher
proportional dem Abstand zwischen Kreis und Abszisse. Die vom Stator aus dem Netz entnom-
mene Wirkleistung P1 ist gleich:
P1 = 3 · U1 · I1P
Da die Verluste im Stator nicht berücksichtigt wurden, wird die Leistung P1 über den Luftspalt auf
den Rotor übertragen. Da sich das magnetische Feld mit der festen Drehzahl ω0 dreht und alle
Kraftwirkungen auf den Rotor durch das magnetische Feld ausgeübt werden, ist das vom Stator
auf den Rotor übertragene Drehmoment proportional der vom Stator aufgenommenen Wirkleis-
tung:
P1 3 3⋅ p
M12 = = · U1 · I1P = ⋅ U1 ⋅ I1P (3.13)
ω0 ω0 ωN
2
1 U1 3p U1 1
(Kipppunkt: I1PKipp = ⋅ → MKipp = ⋅ 2 ⋅ )
2 ωN ⋅ Lσ ' 2 ωN Lσ '
Vernachlässigt man die Luft- und Lagerreibung des Rotors und betrachtet nur stationäre Betriebs-
zustände - also konstante Rotordrehzahl - so wird dieses Moment über die Kupplung an die ange-
kuppelte Arbeitsmaschine abgegeben. Das Drehmoment einer ASM ist also proportional dem Ab-
stand zwischen Kreis und Abszisse.
Aus Abbildung 3.17 ist ersichtlich, dass im Kipppunkt der Läuferstrom I2 um 45° gegenüber U1
verschoben ist. Aus Gleichung 3.9 folgt somit für den Kippschlupf
R '2
sK =
ωn ⋅ Lσ
Der Wirkanteil des Stromes aus Gleichung 3.12 ist damit
R '2 / s sK / s U1
I1W = ⋅ U1 = ⋅
(R 2 / s) + (ωN ⋅ Lσ )
' 2 ' 2
(s K / s) + 1 ωN ⋅ Lσ
2
Mit Gleichung 3.13 folgt für das Drehmoment:
2 ⋅ s ⋅ sK
M = MK · (Kloß`sche Formel)
s2 + s2 K
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

41. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 41 von 108
Für maßstäbliche Zeichnungen wählt man meist den Strommaßstab mi (z. B. in A/mm).
Die Maßstäbe für Leistung und Drehmoment folgen dann:
m P = 3 ⋅ U n ⋅ mi
mP 3 ⋅ Un
mM = = ⋅ mi
ωo ωo
3.2.6 Normierung der Stromortskurve
Bezieht man
- Ströme auf den Nennstrom: I* = I/In
P
- Leistungen auf die Nennscheinleistung: P* =
(3 ⋅ U 1n ⋅ I n )
- Drehmoment auf ein fiktives Moment, das sich aus Nennscheinleistung und synchroner Drehzahl
M
ergibt : M* =
(3 ⋅ U 1n ⋅ I n / ω0 )
so ergibt sich das Kreisdiagramm der ASM in normierter Darstellung, in der die Skalierung der
Ordinate des Kreisdiagramms für I*, P* und M* gleich ist.
i*P P*1 M*12
2
PK
M* K
PA
1 Pn
I *K
M* A
M *n
n
I*
ϕ
I*0 P0 1 2 3 4 5
I*Q
Abbildung 3.18: Stromortskurve des Ständerstromes mit normierten Größen
Das Drehmoment an der Welle ist bei Nennbetrieb immer kleiner als eins, da der Motor außer der
Wirkleistung auch Blindleistung aufnimmt und das Bezugsdrehmoment aus der Scheinleistung
berechnet wurde.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

42. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 42 von 108
Ferner wird oft auch die Drehzahl des Motors auf die synchrone Drehzahl bezogen, also nach
Gleichung (3.3):
n* = ω* = ω0* (1 - s)
sowie auch die Netzfrequenz auf die Nennnetzfrequenz.
Beim Schlupf s = 1 ist die Drehzahl null, hierzu gehört der Punkt Pk, der die Anlaufbedingungen
beschreibt (Kurzschlusspunkt). Der Motor nimmt beim Anlauf den Strom IK* auf und gibt an sei-
ner Welle das Drehmoment MK* ab. Bei Nenndrehzahl nimmt der Motor den Nennstrom In* = 1
auf, der Phasenwinkel ϕ zwischen Strom und Spannung ist maßgeblich für das Verhältnis von
aufgenommener Wirkleistung zu Scheinleistung
P
cos ϕ = (3.14)
S
Der Schlupf des Motors im Nennpunkt (sn) liegt bei 1 % bis 3 %, sodass n* = 0,99 bis 0,97 ist. Bei
Leerlauf des Motors (im Punkt Po) ist das Drehmoment null, der Rotor dreht sich mit der gleichen
Drehzahl wie das Drehfeld (mit synchroner Drehzahl), d. h. n* = 1 und er nimmt den Leerlauf-
strom Io* aus dem Netz auf. Der Leerlaufstrom liegt bei ca. 30 % des Nennstromes, er ist (bei ver-
nachlässigten Eisen- und Reibungsverlusten) ein Blindstrom. Bei negativem Schlupf (unterer Teil
des Kreises) läuft der Rotor schneller als das Drehfeld, das Drehmoment ist negativ. In diesem
Betriebszustand läuft der Motor als Asynchrongenerator, er gibt Wirkleistung in das Netz ab, und
er nimmt aus der angekuppelten Arbeitsmaschine Leistung auf (Hebezeug beim Lastsenken, Ge-
nerator in Windkraftanlagen). Im Gegensatz zu einem Synchrongenerator nimmt eine Asyn-
chronmaschine auch im Generatorbetrieb aus dem Netz induktive Blindleistung auf, der Leis-
tungsfaktor cos ϕ ist immer induktiv.
Arbeitspunkte mit s >> 1 stellen sich ein, wenn der Rotor gegen die Drehrichtung des Drehfeldes
gedreht wird (Gegenstrombremsen, kommt bei Winden vor). Beim Schlupf s = 2 hat der Motor
Nenndrehzahl, und er dreht sich entgegengesetzt zum Drehfeld. Größere Schlupfwerte gefährden
den Motor durch die Fliehkräfte.
3.2.7 Drehmoment-Drehzahl- und Strom-Drehzahl-Kennlinien
Aus der Abbildung 3.18 kann man die Betriebskennlinie M = f (n) und I1 = f (n) entnehmen. Sie
sind in Abbildung 3.19 eingetragen. Man erkennt, dass bei Belastung des Motors die Drehzahl von
der synchronen Drehzahl ausgehend sinkt und das Drehmoment zunächst ansteigt bis zum Kipp-
moment. Nach Erreichen des Kipppunktes sinkt das Drehmoment des Motors. Hat die angekup-
pelte Arbeitsmaschine ein Drehmoment, welches nur wenig mit sinkender Drehzahl abnimmt, so
wird die Motordrehzahl weiter sinken bis zum Stillstand. (Das kann beim Antrieb von Kolben-
pumpen auftreten. Wird der Motor in einem solchen Falle nicht abgeschaltet, so verbrennt er in-
folge des großen Stromes).
Da das Kippmoment nach Gleichung 3.13 quadratisch von der Netzspannung abhängt, bedeutet
eine kleine Abnahme der Netzspannung schon eine erhebliche Verminderung des Drehmomentes.
Um in jedem Fall genügend Reserve für die Beschleunigung des Motors zu haben, muss das
Kippmoment deutlich größer als das Nennmoment sein (Faktor 1,6 ist für die meisten Fälle vorge-
schrieben).
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

43. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 43 von 108
4
Strom I*
3
2
Drehmoment M*
M*, I*
1
0 n*
0 0,5 1 1,5
-1
-2
Abbildung 3.19: Ständerstrom und Drehmoment in Abhängigkeit von der Drehzahl
3.2.8 Aufteilung der Luftspaltleistung
Für den Schutz des Motors ist es wichtig, die Verluste im Rotor zu berücksichtigen. Die über den
Luftspalt zufließende Leistung teilt sich in die Nutzleistung und die Rotorverlustleistung PV2 auf.
PV2* = 3 · I`2*2 · R’2*
Im Stillstand wird die gesamte Luftspaltleistung im Rotor in Wärme umgesetzt.
Nach dem Lehrsatz des Euklid gilt in Abbildung 3.20:
I *2 = x ⋅ d
2
also ist PV2 ~ x. Im Punkt s = 1 ist PK die gesamte aufgenommene Leistung Verlustleistung. PV2
entspricht also der Strecke unterhalb der Linie Po PA . Die Differenz zur aufgenommenen Leistung
wird als mechanische Leistung abgegeben.
P*
2
P
M*
1
Pn
P*mech
I2
PA
I1
sgerade
L eistung
P*V2 Drehmomentgerade
P0 1 x 2 3 4 5 Q*
d
Abbildung 3.20: Heyland-Kreis mit Drehmoment und Leistungen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

44. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 44 von 108
Man erkennt den starken Anstieg der Rotorverluste bei sinkender Drehzahl. Es muss also zum
Schutz des Rotors auf alle Fälle vermieden werden, den Motor durch Überlastung auf große
Schlupfwerte zu bringen. Bei Unterspannung an den Motorklemmen verkleinert sich das Dia-
gramm für die Ströme proportional zur Spannung (Gleichung (3.12)) und das Diagramm für die
Leistungen und Drehmomente proportional zum Quadrat der Spannungen (Die Leistungen und die
Drehmomente sind proportional dem Produkt aus Strom und Spannung). Eine Überlastung des
Asynchronmotors ist also auch bei Drehmomenten unterhalb des Nenndrehmomentes möglich,
wenn die Netzspannung unter ihren Nennwert sinkt.
Mit der Konstruktion nach Abbildung 3.20 ist es möglich, die zu den einzelnen Punkten der
Ortskurve gehörenden Schlupfwerte zu berechnen. Es sind
M* · ω* = P*mech
M* · ωN* = P* = P*mech + P*V2
ω* = ωN* (1 - s)
M* · ωN* (1 - s) = P*mech
*
Pmech
1-s=
Pmech + PV 2
* *
*
PV2
s= * (3.15)
Pmech + PV 2
*
Für den in Abbildung 3.20 eingetragenen Punkt P ist P*mech = 1,13, M* = 1,37, also n* = 0,83. Der
Schlupf an diesem Punkt ist also 17 %.
Der Heylandkreis gilt exakt für das einphasige Ersatzschaltbild, dieses gilt unter folgenden Vor-
aussetzungen:
- symmetrische Maschine und Wicklung
- sinusförmige Feldverteilung im Luftspalt
- keine Sättigung
- keine Stromverdrängung (s. u.)
- sinusförmige Netzspannung
- keine Verluste außer den Läuferverlusten
- stationärer Betriebszustand (!)
Die letzte Voraussetzung bedeutet, dass der Heylandkreis und das einphasige Ersatzschaltbild
nicht für dynamische Vorgänge (z. B. den Einschaltvorgang) gilt.
Für reale Motoren kann die Stromortskurve erheblich von der Kreisform abweichen. Für prakti-
sche Anwendungen ist im vorwiegend genutzten Arbeitsbereich zwischen Leerlauf und Nenn-
punkt eine Approximation durch einen Kreis genau genug möglich.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

45. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 45 von 108
3.2.9 Polumschaltung, Schleifringläufer, Käfigläufer
Die synchrone Drehzahl wird durch die Polpaarzahl festgelegt. Bei vorgegebener Speisefrequenz
können also nur Drehzahlen in der Nähe der synchronen Drehzahlen ausgeführt werden. Bei den
in Europa üblichen 50 Hz-Netzen gibt es also die synchronen Drehzahlen 3.000, 1.500,
1.000,...1/min. An Bord von Schiffen mit überwiegend 60 Hz Netzen gibt es entsprechend 3.600,
1.800, 1.200 1/min... Betrieb mit vergrößertem Schlupf ist nur möglich, wenn der Rotorwiderstand
R2 vergrößert wird. Die Rotorverluste können dann aber nicht aus der Maschine abgeführt werden,
d. h. der Rotor muss mit einer Drehstromwicklung ausgeführt werden. Die drei Wicklungen wer-
den im Stern geschaltet und die drei Anschlüsse werden über Schleifringe und Bürsten mit einem
außerhalb der Maschine liegenden dreisträngigen Widerstand (Schleifringläufer) verbunden.
Durch Verstellen des Widerstandes kann die Position des Punktes Pk auf dem Kreis verändert
werden. Die Lage und die Größe des Kreises bleibt dabei unverändert. Für jedes vorgegebene
Drehmoment kann damit die Drehzahl vom Nennwert in der Nähe der synchronen Drehzahl (Au-
ßenwiderstand im Rotorkreis = null, d. h. Schleifringe kurzgeschlossen) auf beliebig kleine Werte
herabgesetzt werden. Eine Drehzahlregelung wird damit kaum gemacht, der Widerstand wird
durch Schaltwerke stufenweise verstellt. Diese Anordnung wird jedoch gelegentlich benutzt, um
beim Einschalten des Motors ein großes Drehmoment bei verhältnismäßig kleinem Anlaufstrom
zu erreichen. Nach dem Anlauf werden die Schleifringe kurzgeschlossen. Für viele industrielle
Anwendungen sind Motoren mit Schleifringläufer aber ungeeignet, wegen der erforderlichen War-
tung der mechanischen Teile (insbesondere der Kohlebürsten).
Eine nahezu verlustlose Schlupfregelung ist möglich, wenn man die Schleifringe des Rotors an
einen elektronischen Frequenzumrichter anschließt, der den Rotorstrom mit der Frequenz s · ωN
in einen Strom mit Netzfrequenz ωN wandelt und der gleichzeitig die Rotorspannung in die Netz-
spannung umwandelt. Dann kann der Ausgang des Umrichters an das Netz angeschlossen werden
und die dem Rotor zwecks Schlupfregelung entnommene Leistung an das Netz zurückgegeben
werden.
Für manche Antriebe genügt eine stufenweise Umschaltung der Drehzahl, (einfache Winden und
Kräne). Hier besteht die Möglichkeit, zwei Statorwicklungen mit unterschiedlicher Polpaarzahl in
den Stator einzubauen oder Wicklungsteile der Statorwicklung so umzuschalten, dass sich die
Polpaarzahl ändert (Dahlander-Schaltung). Wenn der Rotor eine Wicklung aus miteinander ver-
bundenen Stäben hat (Käfigwicklung), tritt die Wirkung als Kurzschlusswicklung für jede Polzahl
ein, sodass im Rotor keine Umschaltung erforderlich ist.
Die weitaus meisten Antriebe haben wegen des einfachen Aufbaus und den geringen Wartungsan-
forderungen Kurzschlussläufermotoren mit Käfigwicklung. Die Rotoren haben in sich geschlosse-
ne Windungen, die aus Stäben bestehen, welche an den Stirnseiten des Rotors durch Ringe mitein-
ander verbunden sind (Abbildung 3.21). Diese „Käfigwicklung“ ersetzt elektrisch und magnetisch
in jeder Beziehung die kurzgeschlossenen Wicklungen im Rotor. Ihre Wirkungen sind unabhängig
vom Drehwinkel des Rotors, da die „Käfigwicklung“ symmetrisch am Umfang verteilt ist.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

46. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 46 von 108
Nutschlitze
Kern aus
Eisenblech
Stäbe in Nuten
übliche Stabformen
Kurzschlussring
Abbildung 3.21: Aufbau eines Käfigläufers
Abbildung 3.22: Drehstromasynchromotor mit Kurzschlussläufer,
Nennleistung 1,1 kW, synchrone Drehzahl 3.000 min-1
(Seitenansicht und Stirnansicht mit Querschnitten)
1 Lüfter 5 Ständernut
2 Ständerwicklung 6 Stab des Kurzschlusskäfigs
3 Ständerblechpaket 7 Kurzschlussring
4 Läuferblechpaket 8 Läufernut
3.2.10 Stromverdrängungsläufer
Die Kennlinien des Drehmomentes (Abbildung 3.19) zeigen, dass das Anlaufmoment kleiner sein
kann als das maximale Moment.
Der Widerstand R2 der Rotorwicklung wird durch den Querschnitt der Stäbe und der Ringe und
durch das Material festgelegt. Ein zur Erzielung eines großen Anlaufdrehmomentes erforderlicher
großer Widerstand R2 kann nicht einfach durch Verkleinerung der Querschnitte realisiert werden,
da die beim Anlauf auftretende Verlustenergie eine zu hohe Erwärmung der Stäbe und Ringe zur
Folge haben würden. Eine große Wärmekapazität bei hohem elektrischem Widerstand der Rotor-
wicklung (und gleichzeitig große mechanische Festigkeit) wird durch elektrisch schlechter leiten-
des Material (Messing, Aluminium) erreicht.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

47. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 47 von 108
Für die Festlegung des Rotorwiderstandes R2 sind zwei Kriterien wesentlich: R2 soll klein sein,
damit bei Nennbetrieb die Rotorverluste klein sind und R2 soll groß sein, damit das Anlaufdreh-
moment des Motors groß ist. Beide Forderungen werden annähernd durch einen „Stromverdrän-
gungsläufer“ erfüllt. Durch die im Folgenden beschriebene Stromverdrängung verändern sich R2
(und auch Lσ2) abhängig der Drehzahl, so das beide Kriterien erfüllt sind.
Abbildung 3.23: Die Position eines Stabes bestimmt die Größe der Streuinduktivität
Die Wicklungsstäbe in den Nuten erzeugen magnetische Streufelder. Die Feldlinien umschlingen
die erzeugenden Stäbe. Da der magnetische Leitwert des Eisens groß ist, wird die Feldstärke in der
Nut nur durch die Nutbreite b und den Strom i im Wicklungsstab bestimmt:
i
Bσ = µo
b
Der Streufluss, welcher den Stab umschlingt, ist proportional B und dem Abstand h zwischen Stab
und Nutöffnung (und der Maschinenlänge l)
h ⋅l
Φσ = Bσ · h · l = µo ·i
b
Der durch die Nutabmessungen und die Maschinenlänge bestimmte Faktor µo · h · l/b ist die
Streuinduktivität Lσs des Stabes. Die Rotorstreuinduktivität Lσ2 ist im Wesentlichen (bis auf den
Anteil der Kurzschlussringe) diesem Wert proportional. Es besteht nun die Möglichkeit, den Rotor
mit zwei „Kurzschlusskäfigen“ auszurüsten. Die Stäbe des unteren Käfigs liegen am Grunde einer
tiefen Nut, und haben einen kleinen ohmschen Widerstand. Die Stäbe des oberen Käfigs liegen in
flachen Nuten in der Nähe des Luftspaltes und haben einen großen ohmschen Widerstand. Ver-
bindet man die Enden aller Stäbe durch gemeinsame Kurzschlussringe, so ergibt sich ein Ersatz-
schaltbild gemäß Abbildung 3.24.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

48. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 48 von 108
Rso sωN Lσso Rso sωN Lσso
Rsu sωN Lσsu Rsu sωN Lσsu
s = 0,1
s=1
Abbildung 3.24: Prinzip der Stäbe eines Doppelkäfigläufers zur Veranschaulichung, entspricht
die Länge der Symbole den jeweiligen Werten
Beim Anlauf ist der Schlupf groß (s = 1). Die Streureaktanzen bestimmen im Wesentlichen die
Stromaufteilung. Der Strom fließt somit vorwiegend in den oberen Stäben und ein großer Rotor-
widerstand kommt zur Wirkung. Zwar wird auch im Unterkäfig noch ein deutlicher Strom fließen,
dieses ist jedoch ein reiner Blindstrom und bewirkt somit kein Moment; der Punkt s = 100 % liegt
auf der Stromortskurve für den Unterkäfig ganz rechts fast auf der imaginären Achse. Bei kleinem
Schlupf, in der Nähe der Nenndrehzahl, sind die Streureaktanzen klein und die Widerstände sind
daher parallel geschaltet. Der Strom fließt im wesentlich in den unteren Stäben. Der Nennpunkt Pn
liegt also auf einem kleineren Kreis als der Anlaufpunkt Pk. Wegen des im Anlauf wirksamen gro-
ßen Rotorwiderstandes hat der Anlaufstrom eine große Wirkkomponente, und daher ist auch das
Anlaufdrehmoment hoch.
s=100%
2.0 - Real
s=100%
1.0 s=10%
Oberkäfig
s=10%
Unterkäfig Gesamt
1.0 2.0 3.0 4.0 5.0 6.0 7.0 - Imaginär
2.0 - Moment Gesamt
1.0 Oberkäfig
Unterkäfig
0.2 0.4 0.6 0.8 - Drehzahl
4.0 - Strom I1
Gesamt
3.0 Unterkäfig
2.0
Oberkäfig
1.0
0.2 0.4 0.6 0.8 - Drehzahl
Abbildung 3.25: Ortskurve des Läuferstromes, das Drehmoment und den Ständerstrom für eine
Maschine mit Doppelkäfig. Zum Vergleich sind auch die Kurven eingetragen,
die sich ergeben, wenn nur der Unterkäfig oder nur der Oberkäfig vorhanden
ist.
Eine weitere Konstruktion von Stromverdrängungsläufern ist mit Hochstäben möglich. Hierbei
wird der Effekt ausgenutzt, dass bei höheren Frequenzen jeder Strom das Bestreben hat, sich nur
im Oberflächenbereich von Leitern zu bewegen, das entspricht etwa dem Fall, dass in Abbildung
3.23 die beiden Leiter in derselben Nut lägen.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

49. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 49 von 108
Im Anlaufpunkt, also bei s = 1, ist die Läuferfrequenz gleich der Netzfrequenz. Besteht die Läu-
ferkäfigwicklung aus rechteckförmigen Hochstäben im Blechpaket, so fließt bei dieser Frequenz
der Strom nicht mehr über den Leiterquerschnitt gleichmäßig verteilt. Der wirksame ohmsche Wi-
derstand dieses Stabes ist damit größer als der Gleichstromwiderstand.
Abbildung 3.26: Einige mögliche Formen von Stäben in Stromverdrängungsläufern
Bei Normmotoren werden die Rotoren im Allgemeinen mit Aluminiumwicklungen ausgeführt, die
Käfigwicklung wird direkt durch Druckguss in die Nuten des Rotorblechpaketes eingebracht und
die Kurzschlussringe werden im selben Arbeitsvorgang erzeugt. Die Nutenformen können weitge-
hend den elektrischen Bedürfnissen angepasst werden, die Drehzahl-Drehmomentkennlinien kön-
nen dem gewünschten Verlauf gut angenähert werden.
Für Motoren mit häufigen Ein- und Ausschaltungen sind Leichtmetalldruckgusswicklungen nicht
geeignet wegen mangelhafter Temperaturwechselfestigkeit. Derartige Motoren erhalten besser
Stabwicklungen, wobei die Stäbe von Oberkäfig und Unterkäfig in einer gemeinsamen Nut oder in
getrennten Nuten liegen können.
3.2.11 Mechanisches Modell für den Asynchronmotor
Im Luftspalt der Maschine wird ein umlaufendes magnetisches Feld beobachtet, welches von den
stillstehenden Statorwicklungen erzeugt wird. Bezüglich des Luftspaltes und des Rotors kann man
sich auch vorstellen, dass das Feld durch eine mit synchroner Drehzahl rotierende gleichstrom-
durchflossene Wicklung erzeugt wird. Man kommt damit zu einem Ersatzbild des Asynchronmo-
tors in Form einer Schlupfkupplung. Diese Kupplung kann bezüglich ihrer Drehmomente und ih-
rer Eingangsleistung, Ausgangsleistung und Verlustleistung mit einer mechanischen Kupplung
verglichen werden. Im Gegensatz zu einer mechanischen Friktionskupplung verbleibt beim Asyn-
chronmotor ein kleiner belastungsabhängiger Schlupf.
M M
s=
ω1 ωmech
P1=Mω1
PmechM ωmech=P1(1-s)
Pverl=P1-P2=M(ω1-ωmech)=P1s
Abbildung 3.27: Analogie zwischen Asynchronmotor und mechanischer Rutschkupplung
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

50. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 50 von 108
3.2.12 Verluste von Asynchronmotoren und mechanischen Kupplungen bei Beschleuni-
gungsvorgängen
Im Leerlauf treten nur Verluste auf, wenn die Kupplung eingelegt wird bzw. der Motor einge-
schaltet wird und dann die angekuppelten Schwungmassen beschleunigt werden. Bei häufigen
Schaltvorgängen sind diese Verluste weitaus größer als diejenigen bei Nennbelastung.
Die treibende Kupplungsscheibe bzw. das Drehfeld eines Asynchronmotors läuft mit ω1, die Ab-
triebswelle mit ω2 um. Dann ergibt sich das Prinzipbild gemäß Abbildung 3.28:
ω1 ω2
M
M1 M2 MB
J
Abbildung 3.28: Analogie: Beschleunigen einer Schwungmasse J über eine Rutschkupplung
(MB: beschleunigendes Moment)
M1 = M 2 = M
P1 = ω1 M
P2 = ω2 M
PV = P1 - P2 = M (ω1 - ω2)
Im Leerlauf (also bei M =0) ist:
M = MB beschleunigendes Moment
dω2
M=J (J ist das Massenträgheitsmoment des Antriebs)
dt
dω2 d ⎛1 ⎞
P2 = J ω2 = ⎜ J ω2 ⎟
2
dt dt ⎝ 2 ⎠
dω2 d 1
PV = J (ω1 - ω2) = (J (ω1ω2 - ω22))
dt dt 2
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

51. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 51 von 108
t
1
Ekin = ∫
o
P2 dt =
2
J ω22 kinetische Energie
t
1
EV = ∫ o
PV dt = J (ω1ω2 -
2
ω22) Verlustenergie
Die kinetische Energie und die Verlustenergie können in einem Flächendiagramm dargestellt wer-
den:
ω2 Ev
ω1ω2−1/2ω22=
J
ω1
Auf dieser Kurve liegen alle Betriebspunkte
ω2
ω2 ω1
Ekin
1/2ω22=
J
Abbildung 3.29: Kinetische Energie und Verlustarbeit zu einem Zeitpunkt, in dem die Rotor-
drehzahl ω2 noch nicht die Drehfelddrehzahl ω1 erreicht hat.
Am Ende des Hochlaufes ist ω2 = ω1 und EV = Ekin. Die im Rotor während des Anlaufes in Wärme
umgewandelte Verlustenergie ist also gleich der kinetischen Energie des Antriebs! Bei häufigen
Anlaufvorgängen tragen die Anlaufverluste ganz erheblich zur Erwärmung des Rotors bei.
Abbildung 3.30: Kinetische Energie und Verlustarbeit am Ende eines Leer-Anlaufvorganges
ω2
Ev
J
Ekin
J
ω2
ω1
Wenn der Kuppelvorgang zurzeit tA mit der Anfangsdrehzahl ωA des Rotors beginnt, treten fol-
gende Verhältnisse auf:
t
EV = ∫
o
PV dt
da ω2 eine Funktion von t ist, und für t = to die Drehzahl ω2 = ωo ist, gilt:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

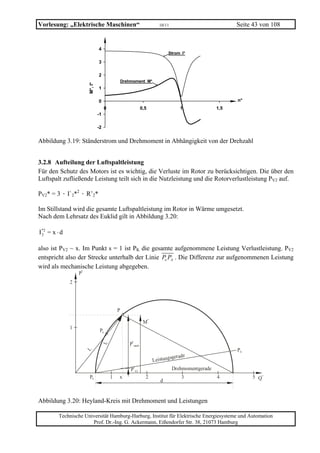
52. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 52 von 108
ω
⎡ 1 ⎤ 2
EV = J ⎢ ω1ω2 − ω2 ⎥
2
⎣ 2 ⎦ ωA
1 1
EV = J [ω1ω2 - ω1ωA - ω22 + ωA2]
2 2
ω2
Verlustenergie in der Kupplung
ω1
Zunahme der kinetischen Energie
während die Kupplung eingeschaltet ist.
ωΑ ω2 ω1
Ekin
kinetische Energie zur Zeit t0 : =1/2ω02
J
Abbildung 3.31: Kinetische Energie und Verlustarbeit bei einem Anlauf von einer Drehzahl ωA
aus.
Beim Schalten der Kupplung über Drehzahlstufen wird insgesamt Verluste-Energie eingespart.
Bei einem Asynchronmotor entspricht das dem Einschalten über eine Drehzahlstufe mit kleinerer
Nenndrehzahl (größer Polzahl der Wicklung)
ω2 Verlustenergie in der Kupplung
ω12 kinetische Energie
ω11
ω11 : Drehzahl der ersten Getriebestufe
ω12 : Drehzahl der zweiten Getriebestufe
Abbildung 3.32: Kinetische Energie und Verlustarbeit bei Anlauf mit zwei Übersetzungsstufen
(Polpaarzahl umschaltbar)
Die größte Einsparung an Verlustenergie ergibt sich bei gleichen Drehzahlstufen.
Der Bremsbetrieb von Kupplungen oder Asynchronmotoren tritt auf, wenn die Ausgangsdrehzahl
ωA größer als die Antriebsdrehzahl ω1 ist (bzw. die Drehfelddrehzahl).
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

53. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 53 von 108
1 1
EV = J [ω1ω2 - ω1ωA - ω22 + ωA2]
2 2
ω2
Verlustenergie in der Kupplung
(evtl. in der Bremse bei ω1=0)
ω1
ω2
ω2 ωΑ
Rückspeisung in das Netz
ERück=Jω1(ω2-ω0)
Abbildung 3.33: Energieanteile bei Abbremsen von einer übersynchronen Drehzahl ωA
Z. B. treten bei der Abbremsung eines Motors aus der Synchrondrehzahl einer vierpoligen Stufe
mit der Drehzahl ωA auf eine achtpolige Stufe mit der Drehzahl ω1 und anschließender Abbrem-
sung auf Stillstand mit der mechanischen Bremse folgende Energiebeträge auf:
ω2
ωΑ
4-polig
Verlustenergie im Rotor
ω1
8-polig Rückspeisung in das Netz
ω2
ω1 ωΑ
Verlustenergie in der Bremse
Abbildung 3.34: Energieanteile bei Abbremsen aus 4-poliger Stufe über 8-polige Stufe und dann
mechanische Bremse
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

54. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 54 von 108
3.2.13 Betrachtung zur Größenordnung der Verlustenergie in einem Hebezeugmotor für
ein Frachtschiff
Beispiel: Polumschaltbarer Ladewindenmotor
Typ SSW 1 BP 2 205 440 V, 60 Hz
Polzahl 28 8 4
n0 257,0 900,0 1.800,0 1/min
nn 200,0 870,0 1.760,0 1/min
s 22,0 3,00 2,20 %
Pn (bei S3-Betrieb) 4,4 19,00 38,00 kW
ωn 22,0 91,00 184,00 s-1
Mn 200,0 209,00 207,00 Nm
In 38,0 55,00 69,00 A
cos ϕn 0,52 0,80
Pel 21,80 42,10 kW
S3-Betrieb bedeutet, dass diese Leistung für Aussetzbetrieb gilt. Bei Dauerbetrieb (S1) wäre nur
eine kleinere Leistung zulässig.
Massenträgheitsmoment J: 1,2 kgm2
Beim direkten Einschalten der vierpoligen Stufe ist:
1
EV = 1,2 kgm2 3,53 104 s-2 = 21,2 kWs
2
Der Motor hat einen Nennschlupf von 2,2 %, daher ist bei Nennbetrieb die in den Rotor geführte
Verlustenergie/Sekunde gleich 0,022 · 38 kW = 0,84 kW. Jeder Anlauf entspricht also 25 s Voll-
lastbetrieb.
Bei Anlauf über die achtpolige Wicklung treten zunächst die Verluste beim Hochlauf auf die halbe
Drehzahl auf:
1
EV8 = EV
4
Danach beim Hochlauf von halber Drehzahl auf die synchrone Drehzahl der vierpoligen Stufe:
ω
⎡ 1 2⎤ o ⎡ 2 1 2 1 2 1 2⎤
EV4,8 = J ⎢ ωo ω − ω ⎥ = J ⎢ωo − ωo − ωo + ωo ⎥
⎣ 2 ⎦ ωo ⎣ 2 2 8 ⎦
2
1 1
EV4,8 = J ωo = E kin
2
8 4
Die gesamte Rotorverlustenergie bei Anlauf über die achtpolige Stufe ist also nur halb so groß wie
die Rotorverlustenergie beim direkten Einschalten der vierpoligen Stufe.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

55. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 55 von 108
Belastung und Beschleunigung
Im Betrieb eines Hebezeuges treten Beschleunigungsdrehmomente MB und lastabhängige Mo-
mente ML auf.
ML = konst. bei einem Hubvorgang
dω
MB = J
dt
M = MB + ML
Die Verluste im Rotor sind dann:
dω
PV = M (ω0 - ω) = J (ω0 - ω) + ML (ωo - ω)
dt
ω (t ) t
EV = J ∫
ωA
(ωo - ω) dω + ML ∫
tA
(ωo - ω) dt
Die Drehzahl ω0 wird nicht ganz erreicht, es verbleibt der Betriebsschlupf sn nach Beendigung des
Beschleunigungsvorganges.
Vernachlässigt man sn, so ist der erste Term unabhängig vom ML (nach dem Hochlauf ist ω(t)
∼ ω0).
t
1
EV = J (ωo - ωA)2 + ML
2 ∫
tA
(ωo - ω) dt
Der zweite Term ist abhängig von t, er steigt ständig weiter, da die Drehzahl ω0 wegen des Be-
triebsschlupfes nicht ganz erreicht wird.
Für die Berechnung des zweiten Terms muss ω = f(t) bekannt sein. Das Drehmoment des Motors
M ist im Allgemeinen als f(ω) gegeben, zu jedem Asynchronmotor gehört eine Kurve M = f(ω).
Für Hebezeugantriebe wird sehr oft ein vierfach-polumschaltbarer Motor mit 28, 8, 4 und 2 Polen
benutzt. Der Motor besteht aus zwei Statoren in einem Gehäuse und zwei Rotoren, die ohne Zwi-
schenlager auf einer Welle angeordnet sind. Ein Teilmotor trägt die 28polige Wicklung, er wird
nur zum Anheben und Absetzen der Last und zum elektrischen Abbremsen benutzt. Der andere
Teilmotor trägt die achtpolige und die vierpolige Wicklung.
Die vierpolige Wicklung ist für den normalen Lasthebebetrieb vorgesehen. Sie kann bei Teillast
oder Leerlauf in eine zweipolige Wicklung umgeschaltet werden (Dahlander-Umschaltung). Die
achtpolige Wicklung ist im Wesentlichen für die Anlaufvorgänge erforderlich.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

56. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 56 von 108
Abschnittsweise linearinierte Drehzahl-Drehmomentkurven:
ω* ist auf vierpolige Synchrondrehzahl bezogen
28polig 8polig 4polig 2polig
ω* M* ω* M* ω* M* ω* M*
-.1400 2.6477 0.0000 3.6324 0.0000 2.0131 0.0000 1.2473
.0767 1.3676 .3000 2.5821 .4933 1.9694 .3333 1.0832
.1200 .6346 .4533 1.2691 .8200 1.7287 1.2800 1.3239
.1427 0.0000 .4900 .4376 .9167 1.4442 1.6467 1.2254
.1 860 -1.5536 .5100 -.4376 .9600 .8753 1.9333 .8972
.1927 -2.4508 .5400 -1.2691 1.0000 0.0000 2.0000 0.0000
.3333 -2.5383 .8333 -3.8293 1.0367 -1.4223 2.2000 -4.5952
1.0000 -1.6630 1.0697 -4.8140 1.1233 -2.0569
2.2000 -1.0284 2.2000 -4.3326 1.4733 -2.7571
1.7067 -3.9387
2.2000 -3.4136
Die Drehzahl-Drehmomentkurven hängen in ihrem Verlauf von der Netzspannung und der Netz-
frequenz ab. Da diese Werte auf Schiffen nicht genau auf ihre Nennwerte gehalten werden kön-
nen, sind Abweichungen der Drehmoment-Drehzahlkennlinien in Rechnung zu stellen. Für die
Untersuchung des Betriebsverhaltens von Hebezeuganlagen genügen daher angenäherte Werte,
die durch lineare Interpolation zwischen wenigen Stützstellen berechnet werden können.
Die folgenden Diagramme zeigen die Verlustleistungen und die gesamten Verlustenergien in den
beiden Maschinenteilen für drei verschiedene Fälle, die diese Zusammenhänge demonstrieren.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

57. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 57 von 108
polumschaltbarer Motor, AEG, 80 kW, 60 Hz
4.0 M*
8-polig
4-polig
2.0
2-polig
0.0 0.5 1.0 1.5 2.0 n*
-2.0
28-polig
-4.0
Abbildung 3.35: M = f(n), abschnittsweise linearisiert für einen Motor 80 kW, 4-fach polum-
schaltbar
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

58. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 58 von 108
4.0 Wärme in 28-poligem Teil
2.0
4.0 Wärme in 2-4-8 poligem Teil
2.0
4.0 PV2 in 28-poligem Teil
2.0
4.0 PV2 in 2-4-8 poligem Teil
2.0
2.0 Motor-Moment
0.0
-2.0
2.0 Drehzahl und synch. Drehzahl
0.0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 s
-2.0
Abbildung 3.36: Simulation folgenden Lastspiels mit einer Last von M * = 0,4:
L
Heben: 0-1-2-3-4
Bremsen: 4-3-1-0
Senken: 0-1-2-3-4
Bremsen: 4-3-1-0
Zum Vergleich:
Heben: 0-4
Bremsen: 4-1-0
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

59. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 59 von 108
4.0 Wärme in 28-poligem Teil
Stufen 0-1-2-3-4-3-1-0 Stufen 0-4-1-0
2.0
4.0 Wärme in 2-4-8 poligem Teil
2.0
4.0 PV2 in 28-poligem Teil
2.0
4.0 PV2 in 2-4-8 poligem Teil
2.0
2.0 Motor-Moment
0.0
-2.0
2.0 Drehzahl und synch. Drehzahl
0.0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 s
-2.0
Abbildung 3.37: Vergleich der Wärmeentwicklung zwischen
a) Anlauf- und Bremsvorgang über Stufen
b) Anlauf- und Bremsvorgang ohne Stufen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

60. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 60 von 108
3.2.14 Anmerkungen zu instationären Betriebszuständen
Alle bisherigen Betrachtungen gelten für den Fall, dass die Maschine sich elektrisch und magne-
tisch in einem stationären Zustand befindet. Die folgende Abbildung (3.38) zeigt den Anlauf eines
Asynchronmotors mit einer Anlaufzeitkonstanten TA = 0,15 s (TA = ωn · J/Mn). Die dicken Linien
zeigen die Verläufe aus Rechnungen mit einem Modell, das auch instationäre elektrische und
magnetische Vorgänge richtig abbildet. Die dünnen Linien zeigen die Verläufe, die mit dem Hey-
land-Kreis ermittelt wurden, wobei der Heyland-Kreis aus den angegebenen Werten für den Leer-
laufstrom und das Kippmoment konstruiert wurde (Als Strom ist hierfür der Scheitelwert gezeich-
net). Wesentliche Unterschiede ergeben sich hauptsächlich im Verlauf des Drehmomentes. Dieser
Gesichtspunkt ist wichtig, wenn die Belastung der Kupplung oder mögliche Drehschwingungen
untersucht werden sollen. Ferner ist interessant, dass für die hier gewählte Maschine die Drehzahl
kurzzeitig sogar die synchrone Drehzahl überschreitet.
Diese beispielhafte Rechnung wurde für einen vergleichsweise kleinen Motor durchgeführt. Bei
größeren Motoren können die starken anfänglichen Drehmomentschwankungen erheblich länger
andauern (bei einem 1 MW-Motor z. B. schon mehr als 1 s).
Insgesamt ist der Heyland-Kreis also auch für die Berechnung von Strom und Drehzahl bei me-
chanischen Ausgleichsvorgängen brauchbar. Entsprechendes gilt für die stationären Kennlinien
von Maschinen mit Stromverdrängungsläufer.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

61. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 61 von 108
5.0 Strom
0.0
-5.0
1.0 Drehzahl
100 200 300 ms
2.0 Moment
1.0
0.0
-1.0
-2.0
Abbildung 3.38: Anlauf eines Asynchronmotors
Dicke Linien: Gerechnet mit einem Modell, das für transiente Vorgänge geeig-
net ist
Dünne Linien: Zum Vergleich mit Hyland-Kreis gerechnet
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

62. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 62 von 108
3.2.15 Einphasiger Asynchronmotor
Für kleine Leistungen (≈ 1 kW) ist es sinnvoll, Asynchron-
motoren mit Käfigläufer für den Anschluss an das (einphasi- Drehrichtung
ge) Wechselstromnetz zu bauen. Zum Verständnis der Funk- t1 t2 t3
tionsweise geht man am besten davon aus, dass von einer
normalen Drehstromasynchronmaschine nur ein Strang an
einer Wechselspannung angeschlossen ist. Die beiden ande-
ren Stränge seien nicht vorhanden. Ein Drehfeld kommt t3 t2 t1 Drehrichtung
dann nicht zu Stande, es ergibt sich vielmehr ein räumlich
feststehendes Feld, das ebenso wie die anliegend Wechsel-
spannung periodisch seine Richtung umkehrt.
Da aber auch die Überlagerung (Addition) von zwei entge- t1 stehend
gengesetzt drehenden "normalen" Drehfelder genau so ein t2
Feld ergibt (Abbildung 3.39), kann man für die Analyse um-
gekehrt annehmen, dass das Feld von zwei normalen an
Drehstrom angeschlossen dreisträngigen Wicklungen erzeugt t3
sei, deren Drehsinn entgegengesetzt geschaltet ist. Ein auf
dem Rotor der Maschine sitzender Beobachter hätte keine M
Möglichkeit, zu entscheiden, ob das von ihm beobachtete Feld
eine Überlagerung zweier entgegengesetzter Drehfelder ist mit gesamt
oder ob es von einer einzelnen einphasigen Wicklung erzeugt -1 -0,5 0,5 1 n/no
ist.
gegen
Beide Drehfelder erzeugen, ebenso wie in einer "normalen"
Asynchronmaschine, ein von "ihrem" Schlupf abhängiges
Drehmoment, und aus der Addition ergibt sich dann das ge- Abbildung 3.39: Stillstehendes Wech-
samte Dehmoment der Maschine. (Abbildung 3.39) Man er- selfeld als Überlage-
kennt, dass die unbelastete Maschine offensichtlich nicht an- rung zweier entge-
laufen kann, weil das Drehmoment bei Stillstand gleich null gengesetzt rotieren-
ist. Gibt man aber dem Rotor im Stillstand einen Anstoß in der Drehfelder
der einen oder der anderen Richtung, dann überwiegt das
Moment in dieser Richtung sofort und die Maschine läuft bis knapp zur Leerlaufdrehzahl hoch.
Sie ist dann auch mit etwa Nennmoment belastbar, allerdings entstehen durch das bremsende
rückwärtslaufende Feld (Gegenfeld) zusätzliche Verluste. (Deshalb wird bei normalen Asyn-
chronmaschine oft während des Betriebes überwacht, dass die Spannungen für alle Stränge vor-
handen sind.)
Für den einphasigen Betrieb muss also zumindest für den Anlauf ein Drehfeld "künstlich" erzeugt
werden.
Dafür gibt es verschiedene Möglichkeiten:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

63. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 63 von 108
Kondensatormotor
I
Ia Ua
Uc
Ua Uc
Ib Ia
ϕ
Ib
Ub ϕ
Ub
Abbildung 3.40: Kondensatormotor mit zugehörigem Zeigerdiagramm
Eine häufig anwendete Methode (z. B. Umwälzpumpe in Hausheizungsanlage, Stellmotor für Re-
gelventile) ist die, dass die Phasenverschiebung in einem Kondensator dazu ausgenutzt wird, eine
gegenüber der Netzspannung phasenverschobene Hilfsspannung zu erzeugen, die dann einen
zweiten Strang des Motors versorgt. Die beiden Stränge eines solchen Motors sind typisch senk-
recht zueinander angeordnet. Das Zeigerbild macht deutlich, wie auf diese Art zwei um 90° ver-
setzte Spannungen entstehen, die zusammen mit den um räumlich 90° versetzten Strängen in der
Maschine ebenso wie bei Drehstrom ein Drehfeld erzeugen. (Unterschiedliche Beträge können
leicht durch die Windungszahl ausgeglichen werden.) Da der Kondensator nur für einen Betriebs-
punkt optimal gewählt werden kann, gibt es auch Anordnungen, in denen der Hilfsstrang nach
dem Hochlauf abgeschaltet wird, oder die Kapazität des Kondensators umgeschaltet wird.
Andere Varianten
Andere Varianten sind heute durch Motoren mit elektronischer Ansteuerungen weitgehend ver-
drängt. Dennoch ist es interessant, dass sich auch auf magnetische Art erreichen lässt, dass der
Fluss in der Maschine in zwei räumlich versetzten Richtungen auch zeitlich phasenverschoben ist
und sich so ein Drehfeld bildet, das für den Anlauf ausreicht. Bis vor 20 Jahren waren z. B. Spalt-
polmotoren sehr verbreitet (Schallplattenspieler, Uhren): Eine einsträngige Wicklung (meist um
ausgebildete Pole, ähnlich wie die Erregerwicklung einer Gleichstrommaschine) erzeugt das Feld.
Ein Teil jeden Poles ist von einer zweiten Wicklung umschlungen, die kurzgeschlossen ist. Dieser
Kurzschluss verzögert den Aufbau und den Abbau des magnetischen Feldes in dem umschlunge-
nen Teil des Poles gegenüber dem Fluss in dem nicht umschlungen Teil und sorgt so für die erfor-
derliche Phasenverschiebung.
Bei einer anderen Variante wurde die Hysterese des Eisens ausgenutzt, um über die Remanenz des
Eisens die erforderliche Phasenverschiebung eines Teiles des Flusses zu erreichen.
3.3 Synchronmaschinen
3.3.1 Grundsätzliche Wirkungsweise und Eigenschaften
Eine Synchronmaschine besteht aus dem Stator, der eine symmetrische Drehstromwicklung ent-
hält und einem Rotor (auch „Polrad“ genannt), der in der Regel eine einsträngige Erregerwicklung
trägt. Bei Sonderbauformen wird die Erregung an Stelle der gleichstromdurchflossenen Erreger-
wicklung auch durch Permanentmagnete aufgebracht.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

64. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 64 von 108
Polrad mit
N Erregerwicklung
S Stator mit Dreh-
stromwicklung
Abbildung 3.41: Zweipolige Synchronmaschine
Wenn in den Statorwicklungen symmetrische Drehströme fließen, so entsteht ein Drehfeld kon-
stanter Größe, das mit einer Kreisfrequenz gemäß der Kreisfrequenz der Ströme umläuft. Die die-
ser Frequenz entsprechende Drehzahl ist die synchrone Drehzahl der Maschine:
f
no = (3.15)
p
f : Frequenz der Drehströme
p : Polpaarzahl der Maschine
Der mechanisch unbelastete Rotor wird sich in Richtung des augenblicklichen Feldes einstellen:
N
n
S
Abbildung 3.42: Feldbild der unbelasteten Maschine
d. h., der Rotor läuft ebenfalls mit der synchronen Drehzahl um.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

65. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 65 von 108
Für die Bildung eines Drehmomentes ist ein Strom im Stator erforderlich, der bei den Polen des
Rotors jeweils den maximalen Betrag hat. Ein Strom mit dem maximalen Betrag zwischen den
beiden Polen konnte kein Drehmoment erzeugen, sondern würde nur das durch die Erregerwick-
lung erzeugte Feld verstärken oder schwächen.
Abbildung 3.43a zeigt einen Strom, der auf den Rotor ein Drehmoment entgegen der Drehrichtung
ausübt. Die Maschine nimmt mechanische Leistung auf und wandelt sie in elektrische um. Zu-
sammen mit dem Erregerstrom ergibt sich das in Abbildung 3.43b dargestellte Feldbild. Der Rotor
läuft dem Feld voraus, er „zieht“ also das Feld hinter sich her. Der Winkel zwischen Polrad und
Feld nimmt offensichtlich mit steigendem Drehmoment zu. Dies ist vergleichbar mit einer Dreh-
feder. Bei Betrieb als Motor kehrt sich das Vorzeichen des Statorstromes um und das Feld „zieht“
den Rotor hinter sich her.
Die Herleitungen weiter unten werden zeigen, dass es wie bei der Asynchronmaschine ein Kipp-
moment gibt. Wird das Moment an der Welle größer als das Kippmoment, so reißt der Zusam-
menhang zwischen dem Drehfeld und der Rotorlage ab. Dieser Vorgang wird als „Kippen“ oder
als „außer Tritt fallen“ bezeichnet. Der Rotor dreht dann nicht mehr synchron mit dem Drehfeld
und das entstehende Moment wirkt mal bremsend und mal antreibend. Ein stationärer Betrieb ist
nicht möglich.
n
Abbildung 3.43a: Feld eines Wirkstromes Abbildung 3.43b: Feld der erregten als
im Stator, der auf den Generator belasteten
Rotor bremsend wirkt Maschine
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

66. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 66 von 108
Mit diesen qualitativen Überlegungen sind die hauptsächlichen Eigenschaften der Synchronma-
schine beschrieben:
1. Im Normalbetrieb läuft der Rotor unabhängig von der mechanischen Belastung mit der syn-
chronen Drehzahl um. Die Belastung wirkt sich lediglich auf den Winkel des Rotors relativ
zum Drehfeld aus.
2. Bei zu großem bremsendem oder antreibendem Moment fällt die Maschine außer Tritt.
3. Bei der Inbetriebnahme als Generator oder als Motor muss durch entsprechende Maßnahmen
dafür gesorgt werden, dass Synchronismus zwischen Rotordrehzahl und Drehfeld herrscht.
4. Bei Änderung der mechanischen oder elektrischen Belastung neigt die Maschine zu mechani-
schen Pendelungen des Rotors relativ zum Drehfeld, weil das Drehmoment etwa proportional
zum Winkel zwischen Rotor und Drehfeld ist (also entsprechend einer Feder).
3.3.2 Konstruktive Ausführung, Anwendungen
Elektrisch erregte Synchronmaschinen werden hauptsächlich als „Schenkelpolmaschine“ („Ein-
zelpolmaschine“) oder als „Vollpolmaschine“ ausgeführt.
Abbildung 3.44: Querschnitt durch eine Schenkelpolmaschine (aus: Kleinrath, Grundlagen elekt-
rischer Maschinen, Akademische Verlagsgesellschaft)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

67. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 67 von 108
Eine andere Ausführung des Rotors ist der Trommelläufer („Vollpolmaschine“).
Erregerwicklung
Abbildung 3.45: Querschnitt durch den zylindrischen Rotor einer zweipoligen Vollpolmaschine
Bei kleinen und sehr großen Synchronmaschinen wird der Erregerstrom über Schleifringe zuge-
führt. Im mittleren Leistungsbereich findet man oft eine schleifringlose Ausführung, bei der auf
der Welle eine Erregermaschine vorhanden ist. Dies ist im Prinzip ein Synchrongenerator, bei dem
die Erregerwicklung fest steht und die Drehstromwicklung rotiert. Der induzierte Drehstrom wird
durch einen auf der Welle montierten Gleichrichter in Gleichstrom für die Erregung umgeformt.
Die Erregung der Erregermaschine wird oft durch einen weiteren meist sehr kleinen Generator
erzeugt, der durch einen Permanentmagneten erregt ist. Generatoren dieser Bauart kommen ohne
jede Hilfsspannung aus und sind deshalb besonders für Notstromaggregate geeignet.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

68. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 68 von 108
Die hauptsächlichen Anwendungen der Synchronmaschine sind:
Generatoren:
- Kraftwerksgeneratoren: In Wasserkraftwerken Einzelpolmaschinen, in thermischen Kraftwer-
ken Vollpolmaschinen, Leistungen bis > 1.000 MW
- Bordnetzgeneratoren: auf Schiffen, Flugzeugen und Kraftfahrzeugen
Motoren:
- Propellerantriebe auf Schiffen
- Industrielle Antriebe (vor allem große Einzelantriebe und Mehrmaschinen-Gleichlaufantriebe)
- Servorantriebe für Werkzeugmaschinen und Roboter (Motoren mit Permanentmagneterregung)
- Uhrenantriebe
3.3.3 Betriebsverhalten, Kennlinien
Im Folgenden werden die Verhältnisse nur für die Vollpolmaschine behandelt, weil diese wegen
ihres über dem Rotorumfang konstanten Luftspaltes einfacher beschreibbar ist als die Schenkel-
polmaschine.
Es wird für alle Betrachtungen unterstellt, dass die drei Stränge der Maschine im Stern geschaltet
sind. Man rechnet also stets mit den Leiterströmen und den Sternpunktspannungen. Da man an
den drei Anschlüssen der Maschine ohne zusätzliche Informationen nicht erkennen kann, ob
Stern- oder Dreieckschaltung vorliegt, bedeutet dies keine Einschränkung.
Ferner sollen Wicklungswiderstände im Stator vernachlässigt werden.
Es werden zunächst drei Sonderfälle betrachtet.
a. Polrad erregt, Ständerwicklung stromlos
b. Ständerwicklungen führen Drehstrom, Polrad läuft unerregt synchron um
c. Polrad erregt, Klemmen kurzgeschlossen
3.3.3.1 Leerlaufkennlinie
Im Fall a. misst man an den Maschinenklemmen die Leerlaufspannung U10 als Funktion des Erre-
gerstromes Ie; diese Spannung wird durch den vom Polrad erzeugten Fluss in den Ständerwicklun-
gen mit induziert. Die induzierte Spannung wird Polradspannung genannt. Sie ist proportional
zum magnetischen Fluss Φe des Polrades und der Drehzahl:
Up ∼ Φe · ω und Φe = f (Ie)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

69. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 69 von 108
Im Leerlauf also:
U10 = Up
U10
U1N = Nennspannung
U1N
Ie0 = Leerlauferregerstrom
Ie0 Ie
Abbildung 3.46: Leerlaufkennlinie
Das Abflachen der Kurve bei größeren Erregerströmen ist durch die Sättigung des Eisens bedingt.
3.3.3.2 Synchrone Reaktanz, bezogene Größen
Im Falle b. liegen die gleichen Verhältnisse wie bei einer leer laufenden Asynchronmaschine vor.
Es wird durch die Ständerströme ein Drehfeld erzeugt, das wiederum zu induzierten Spannungen
in den Strangwicklungen führt. Der Quotient aus Strangspannung und Strangstrom (der im Stern
geschalteten Stränge) wird als „synchrone Reaktanz“ Xd bezeichnet, vergleichbar der Leerlaufin-
duktivität der Asynchronmaschine:
U1
Xd = (Ie = 0) (3.16)
I1
Die synchrone Reaktanz Xd setzt sich aus der Hauptreaktanz Xh und der Streureaktanz Xlσ zu-
sammen:
Xd = Xh + Xlσ
Xh beschreibt die Reaktanz des Drehfeldes, das sich über den Luftspalt, das Ständerblechpaket und
den Rotor schließt, Xlσ die Reaktanz der Streufelder der Statornuten und der Wickelköpfe.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

70. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 70 von 108
Um eine bessere Vergleichbarkeit zwischen Maschinen unterschiedlicher Größe zu erhalten, ist es
üblich, alle Reaktanzen als bezogene Größen anzugeben. Dazu wird Gleichung (3.16) um Nenn-
(Sternpunkt-)spannung und Nennstrom erweitert. Bezogene Größen werden mit kleinen Buchsta-
ben bezeichnet.
Xd U I
xd = = 1 ⋅ 1n (3.17)
U Yn / I1n U Yn I1
3.3.3.3 Leerlauf-Kurzschluss-Verhältnis
Im Fall c., d. h. bei kurzgeschlossener Maschine wird durch das Polrad Polradspannung Up indu-
ziert. Da die Spannung bei einem Kurzschluss null ist, muss auch der Fluss in der Maschine null
sein. Der Kurzschlussstrom muss also gerade so groß sein, dass er den Fluss des Polrades aufhebt.
Da Fluss und Spannung wegen konstanter Drehzahl proportional zueinander sind, kann dies auch
so ausgedrückt werden, dass die in der synchronen Reaktanz durch den Kurzschlussstrom indu-
zierte Spannung genauso gleich der vom Polrad induzierten Spannung sein muss, also:
I1K · Xd = Up
Daraus folgt der Kurzschlussstrom:
Up
I1K = (3.18)
Xd
I1K
I1N
I1KO
I1N
Ieo Ie
Abbildung 3.47: Kurzschlusskennlinie
Da der Fluss bei einem Kurzschluss null ist, gibt es keine Sättigung im Eisen und die Kurz-
schlusskennlinie ist deshalb eine Gerade.
Eine charakteristische Größe der Synchronmaschine ist das „Leerlauf-Kurzschlussverhältnis“ KC.
Dies ist das Verhältnis des Kurzschlussstromes, der sich bei Leerlauferregung Ieo (vgl. Abbildung
3.46) einstellt, zum Nennstrom der Maschine.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

71. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 71 von 108
Wegen Up = U1N bei Ie = Ieo gilt mit Gleichung (3.17 und 3.18):
I1Ko U1N 1
KC = = = (3.19)
I1N X d ⋅ I1N x d
Das Leerlauf-Kurzschluss-Verhältnis liegt bei Synchronmaschinen üblicher Bauart bei 0,5 ... 0,9
(Vollpolmaschine) bzw. bei 0,6 ... 1,7 (Schenkelpolmaschine).
Der stationäre Kurzschlussstrom ist also im Vergleich zum Nennstrom nicht allzu hoch.
Bei einem plötzlich auftretenden Kurzschluss ist jedoch kurzzeitig (transient) der Strom sehr viel
größer als der Nennstrom. Stromspitzen bis zum 15-fachen des Nennstromes kommen vor. Die
Wicklungen und Schaltgeräte müssen so ausgelegt sein, dass sie den dadurch entstehenden Kräf-
ten (F ∼ I2) stand halten.
3.3.3.4 Ersatzschaltbild und Zeigerdiagramme
Auf Grund der obigen Betrachtungen kann man das einphasige Ersatzschaltbild entweder als
Spannungsquelle (Abbildung 3.48a) oder als Stromquelle (Abbildung 3.48b) darstellen:
Xd
I1
X1σ X1h
U1 Ui Up Ie
Abbildung 3.48a: Einphasiges Ersatzschaltbild der Synchronmaschine mit Spannungsquelle
Ui: „Innere Spannung“
I1 UP/Xd ~ Ie
U1
Ie
Abbildung 3.48b: Einphasiges Ersatzschaltbild der Synchronmaschine mit Stromquelle
Eine räumliche Darstellung erhält man, wenn die Durchflutungen Θ1 der Ständerwicklung und Θe
des Polrades vektoriell addiert werden; der resultierende Vektor ergibt die augenblickliche Durch-
flutung in Bezug auf die Ständerwicklung 1 und damit das Hauptfeld Φh.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

72. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 72 von 108
φh
e I1
res
Ie
1
Abbildung 3.49: Addition der Durchflutungen von Ständer- und Erregerwicklung
3.3.4 Ortskurve des Ständerstromes
Die Ortskurve der Vollpolmaschine kann aus den Ersatzschaltbildern (Abbildung 3.48) abgeleitet
werden.
U1 = j ⋅ Xd ⋅ I1 + Up
U1 Up
I1 = −
j Xd j Xd
U1 Up
= - j⋅ + j⋅
Xd Xd
Die geometrische Darstellung erhält man aus folgender Überlegung: Legt man die feste Netzspan-
nung U1 in die reelle Achse, dann entspricht der erste Term einem Punkt auf der negativen imagi-
nären Achse. Der Betrag des zweiten Terms ist durch die Erregung gegeben, die Phasenlage ist
jedoch frei und bestimmt den Strom I1. Alle I1 müssen also auf einem Kreis mit dem Mittelpunkt –
j · U1/Xd mit dem Radius UP/Xd liegen.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

73. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 73 von 108
Re
Stabilitätsgrenze
jXdI1
UP U1
Motor ϑ -j.U 1
ϕ Xd
ϑ -Im
I1
Generator j.U P 0,5
Xd
1,0
I e UP
1,5 =
I eo U1
kapazitiv induktiv
Abbildung 3.50: Ortskurven der Vollpol-Synchronmaschine mit dem Zeigerbild für einen Be-
trieb als Generator (UP/Xd ∼ Ie)
In Betriebspunkten der oberen Halbebene in Abbildung 3.50 nimmt die Maschine elektrische
Leistung auf, arbeitet also als Motor. Entsprechend arbeitet die Maschine in den Betriebspunkten
der unteren Halbebene als Generator.
Wenn die Spitze von I1 in der rechten Halbebene liegt, nimmt die Maschine wie eine Induktivität
Blindleistung auf, man spricht dann von „Untererregung“.
Bei „Übererregung“ wirkt die Maschine wie ein Kondensator und gibt Blindleistung an das Netz
ab.
Ein besonderer Fall liegt vor bei ϑ = 0: Für Up > U1 eilt I1 der Spannung U1 um 90° voraus, die
Maschine verhält sich wie ein dreiphasiger Kondensator und gibt reine Blindleistung an das Netz
ab. Synchronmaschinen werden in dieser Betriebsweise als sog. „Phasenschieber“ in Stromversor-
gungssystemen eingesetzt, um den Leistungsfaktor der Netze zu verbessern, d. h. um den Blind-
stromverbrauch z. B. von Asynchronmotoren zu kompensieren. In dieser Betriebsweise ist das
Drehmoment immer 0, die Maschine braucht also keinen Antrieb (außer zum Anfahren).
Anmerkung: In der Literatur wird oft der Strom I1 in Abbildung 3.48 umgekehrt angetragen, die
Ortskurve sieht entsprechend anders aus.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

74. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 74 von 108
3.3.5 Drehmomentbildung
Da eine verlustfreie Maschine vorausgesetzt wird, kann das Drehmoment aus der aufgenommenen
elektrischen Leistung ermittelt werden:
P = 3 ⋅ I1 ⋅ U1 ⋅ cos ϕ (3.20)
(U1 gemäß Abbildung 3.48, also die Sternpunktspannung.)
Aus dem Zeigerbild (Abbildung 3.50) wird nach den Regeln der Trigonometrie entnommen:
⎛π ⎞
sin ⎜ + (π − ϕ) ⎟
⎝2 ⎠ = sin ϑ (Sinus-Satz) (3.21)
UP / Xd I1
⎛3 ⎞
sin ⎜ π − ϕ ⎟ = - cos ϕ (3.22)
⎝2 ⎠
UP
- I1 · cos ϕ = ⋅ sin ϑ (3.23)
Xd
Damit:
Up
P = - 3 ⋅ U1 ⋅ ⋅ sin ϑ (3.24)
Xd
Da eine verlustlose Maschine vorausgesetzt wurde, ist
P = M · 2πn (3.25)
und es folgt das Drehmoment
−3 U
M= ⋅ U1 ⋅ p ⋅ sin ϑ (3.26)
2πn Xd
Dem „Polradwinkel“ ϑ zwischen den Richtungen der Zeitzeiger U1 und Up entspricht in der Ma-
schine räumlich der Winkel zwischen der Polradachse und der Richtung des Ständerflusses. ϑ ist
positiv, wenn der Rotor vor dem Ständerfeld her läuft. Der Rotor „zieht“ das elektrische Netz und
die Maschine arbeitet somit als Generator.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

75. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 75 von 108
M
Stabilitäts-
grenze
−π/2 ϑ
−π π/2 π
Motor Generator
Abbildung 3.51: Drehmoment als Funktion des Polradwinkels
Nach Gleichung (3.26) ist das maximal mögliche Drehmoment (das „Kippmoment“) bei gegebe-
ner Polradspannung umgekehrt proportional zur synchronen Reaktanz Xd. Da Xd umgekehrt pro-
portional zur Dicke des Luftspaltes ist, werden Synchronmaschinen mit relativ großen Luftspalten
ausgeführt.
Wie schon qualitativ beschrieben, „kippt“ die Synchronmaschine bei Polradwinkel ϑ > 90°, d. h.
der Zusammenhang zwischen Drehfeld und Polrad reißt ab und die Maschine kann kein Drehmo-
ment mehr aufnehmen oder abgeben.
Für kleine Auslenkungen aus einer Gleichgewichtslage wachsen die Rückstellkräfte praktisch
proportional zur Auslenkung an. Dies entspricht der Wirkung einer Feder, sodass in Verbindung
mit dem Massenträgheitsmoment des Rotors ein schwingungsfähiges Gebilde entsteht, das eine
mechanische Resonanzfrequenz aufweist. Insbesondere in Verbindung mit pulsierenden An-
triebsmomenten (z. B. von Kolbenkraftmaschinen!) muss die Anlage auf Resonanz geprüft wer-
den.
Zur Dämpfung solcher Schwingungen wird die in Abbildung 3.44 gezeigte Dämpferwicklung ein-
gebaut. Es handelt sich um eine kurzgeschlossene Käfigwicklung wie bei Asynchronmotoren. Das
dadurch erzeugte Drehmoment ist wie bei der Asynchronmaschine proportional zur Differenzge-
schwindigkeit zwischen Ständerfeld und Rotor (Schlupf), wirkt also vergleichbar zu einem visko-
sen Dämpfer.
3.3.6 Betrieb der Synchronmaschine am Netz
Eine Synchronmaschine als Generator kann dann auf das Netz geschaltet werden, wenn die Span-
nungen des Netzes und der Synchronmaschine
- gleiche Drehrichtung (Phasenfolge),
- gleiche Frequenz,
- gleiche Größe und
- gleiche Phasenlage
haben. Die Zeiger der Netzspannung U1 und der Polradspannung UP sind dann deckungsgleich
und auch nach Schließen des Schalters zum Netz fließt kein Strom und es gibt eine sanfte Lastauf-
nahme.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

76. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 76 von 108
Anderenfalls gäbe es mit dem Einschalten einen erheblichen Strom- und Momentenstoß (der auch
zu einem Schaden führen kann) und die Maschine kann sofort außer Tritt fallen.
Die oben genannten Bedingungen werden vor dem Schließen des Schalters geprüft, oft ist eine
automatische Sperre vorhanden, die ein nichtsynchrones Zuschalten verhindern soll.
Eine einfache, jedoch auch relativ ungenaue Synchronisierschaltung ist z. B. die sog. „Dunkel-
schaltung“, bei der Glühlampen zwischen gleichen Phasen des zu synchronisierenden Generators
und des Netzes geschaltet werden:
Netz
G
Abbildung 3.52: Synchronisierschaltung (Dunkelschaltung)
Die Lampen leuchten mit der Differenzfrequenz der Phasenspannungen auf, solange der Synchro-
nismus nicht erreicht ist. Bei gleicher Frequenz jedoch unterschiedlicher Phasenlage leuchten alle
Lampen gleichzeitig, bei 180° Phasenverschiebung leuchten sie mit maximaler Helligkeit. Sind
alle Lampen dunkel, so ist der Generator synchronisiert und der Schalter kann geschlossen wer-
den.
In der Praxis werden statt dieser einfachen Anordnung spezielle Messgeräte (z. B. „Synchro-
noskop“) eingesetzt, die eine genauere Beurteilung ermöglichen.
Für eine Synchronmaschine als Motor gibt es für einen Anlauf folgende Möglichkeiten:
1. Anlauf über Dämpferwicklung (asynchroner Anlauf), also vergleichbar mit einem Asynchron-
motor
2. Hochfahren der Synchronmaschine über einen Anwurfmotor und Synchronisation
3. Frequenzanlauf. Hierzu wird mit elektronischen Schaltmitteln (Thyristoren usw.) eine Span-
nung mit langsam steigender Frequenz und Amplitude erzeugt.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

77. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 77 von 108
3.4 Antriebe mit Frequenzumrichter
3.4.1 Pulswechselrichter
Für Antriebe von wenigen kW bis zu einigen MW werden heute Frequenzumformer mit Pulswei-
tenmodulation (Frequenz einige kHz) und Gleichspannungszwischenkreis eingesetzt.
Abbildung 3.53: Frequenzumrichter mit Gleichspannungszwischenkreis
(GR: Gleichrichter, WR: Wechselrichter)
u
uR ohne C uR mit C
t
iNetz uNetz
t
Abbildung 3.54: Ströme und Spannungen am Gleichrichter (GR),
(hier für einphasige Ausführung), der Verbrauch des Wechselrichter ist verein-
facht durch einen Widerstand nachgebildet.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

78. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 78 von 108
Der Wechselrichter besteht aus Halbleiterschaltern, die die Leitungen L1 – L3 zu dem Motor ge-
mäß Abbildung 3.55 mit dem Gleichspannungszwischenkreis verbinden.
+
Ud
−
U12
L1 L2 L3
U12
Ud
ω 1t
Abbildung 3.55: Prinzip eines Pulswechselrichters
Als Schalter werden spezielle Transistoren eingesetzt. (IGBT, IGCT oder andere)
Die Pulsweite wird so moduliert, dass, der Mittelwert eines Impulses und der zugehörigen Lücke
etwa der dem Sinus entsprechenden gewünschten Spannung entspricht. Die Modulation hat wenig
Einfluss auf das Betriebsverhalten des Motors, jedoch werden Verluste und Geräusche
sehr erheblich von der
genauen Art der Modulation bestimmt.
In neueren Entwicklungen für große Antrieb wird mit mehreren Gleichspannungen unterschiedli-
cher Größe gearbeitet, sodass auch Zwischenstufen geschaltet werden und so die Sinusform noch
besser angenähert werden kann.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

79. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 79 von 108
3.4.2 Leistungsflüsse bei Motorbetrieb und bei Bremsbetrieb
Abbildung 3.56: Leistungsflüsse bei Motorbetrieb und bei Bremsbetrieb
Im Gleichspannungszwischenkreis ist das Vorzeichen der Spannung konstant. Die Umkehrung des
Leistungsflusses bei Bremsbetrieb bedeutet somit auch eine Umkehr des Stromes. Der Strom wird
durch den Bremswiderstand aufgenommen, wobei der vorgeschaltete Transistor als Chopper den
Strom und damit die Bremskraft regelt. Aus anderer Sicht kann das so interpretiert werden, dass
der Chopper den Widerstand nur zeitweise einschaltet und der Widerstand dadurch vergrößert
erscheint. Der Chopper kann den Widerstandwert naturgemäß nicht verkleinern.
Wegen P = U2 / R bedeutet das, dass mit steigender Bremsleistung P auch die Zwischenkreisspan-
nung steigt und unter Umständen den zulässigen Grenzwert überschreitet.
Abbildung 3.57: Zu den Vorzeichen bei Leistungsflüssen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

80. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 80 von 108
Leistung ist immer das Produkt aus 2 physikalischen Größen:
• P=U*I
• P=F*v usw.
Trägt man die beiden Größen entsprechend nebenstehendem Muster als Achsenkreuz auf, dann
erhält man 4 Gebiete (Quadranten), die sich durch die Vorzeichen der Größen unterscheiden.
Je nachdem, in welchem Gebiet der Betrieb möglich ist, spricht man besonders bei Stromrichtern
von 1-, 2-, oder 4-Quadranten Betrieb.
Beispiele:
Batterie-Ladegleichrichter Vorzeichen von U und I sind fest, 1-Quadrant
ein Entladen der Batterie ist nicht
möglich.
Umrichter für Motor mit Drehrichtungs- Motor kann nicht als Generator in 2-Quadrant
umkehr Netz speisen
Umrichter für eine Drehrichtung, Maschi- Nur eine Drehrichtung 2-Quadrant
ne wahlweise als Motor oder als Genera-
tor
Umrichter für beide Drehrichtungen und 4-Quadrant
beide Richtungen des Leistungsflusses
3.4.3 Zur Regelung und Steuerung
Die Drehzahl - Drehmomentenkennlinie von Drehstromasynchronmaschinen ist durch deren Kon-
struktion fest vorgegeben, zumindest bei dem am weitesten verbreiteten Motor mit Käfigläufer.
Frequenzumrichter erlauben es, die Spannung und die Frequenz zu verändern. In Antrieben mit
Frequenzumformern ist die "natürliche" Kennlinie der Asynchronmaschine deshalb nur schwach
erkennbar, wesentliche Merkmale der Kennlinie werden durch die Regelung des Umrichters be-
wirkt.
Abbildung 3.58: Prinzip der Steuerung und Regelung in einem üblichen Frequenzumrichter für
Asynchronmotoren
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

81. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 81 von 108
Für eine genaue Drehzahlregelung ist bei Asynchronmaschinen ein Drehzahlsensor unerlässlich.
Bei vielen Antrieben verzichtet man auf Sensoren an dem Motor. Stattdessen enthält die Steue-
rung des Frequenzumrichters ein Rechenmodell, mit dem - je nach Aufwand - die meisten internen
Größen des Motors berechnet werden können. Diese werden dann als Basis für die eigentliche
Drehzahl benutzt. Es ist klar, dass die Genauigkeit der "Regelung" von der Genauigkeit des Mo-
dells und der Maschinendaten abhängt.
In neueren Entwicklungen ist das Modell so umfangreich, dass die Größe und die Richtung des
Magnetfeldes in der Maschine kontinuierlich berechnet wird und dies Basis für die Steuerung des
Stromrichters genommen wird (Vektor-Regelung, feldorientierte Regelung.) Damit können auch
die dynamischen Eigenschaften des Antriebs ausgezeichnet an die gestellten Anforderungen ange-
passt werden.
Da in der Steuerung des Frequenzumrichters heute immer ein Rechner vorhanden ist, wird dieser
für die Erzeugung des Modells aus einigen wenigen Daten des Motors eingesetzt. Außer den
Nenndaten braucht der Bediener kaum Daten einzugeben.
Neben der eigentlichen Steuerung des Antriebs (Drehrichtungsumkehr, Anfahren, Bremsen, An-
fahren mit Rampe usw.) gibt es oft folgende Besonderheiten in der Regelung:
Schlupfkompensation: Aus dem Nennpunkt der Maschine und dem recht gut schätzbaren Leer-
laufpunkt kann bereits ein Modell erzeugt werden, dass aus den bekannten Strömen und Spannun-
gen den aktuellen Schlupf ermittelt. Der Regler kann mit dieser Information die Frequenz gerade
umso viel höher einstellen, dass "trotz" Schlupf die gewünschte Solldrehzahl fast genau erreicht
wird. Für die Einstellung ist die Kenntnis folgenden Zusammenhanges wichtig: Mit steigender
Maschinentemperatur nimmt der Schlupf etwas zu. Ein genauer Abgleich der Schlupfkompensati-
on bei betriebswarmer Maschine führt dazu, dass bei kalter Maschine die Drehzahl geringfügig zu
hoch ist. In jedem Fall ist die Abweichung zwischen Soll- und Istdrehzahl viel kleiner als bei An-
lagen ohne Schlupfkompensation.
Schlupf-, Momenten-, Strom- oder Leistungsbegrenzung: Überlast oder Kippen des Antriebs kann
damit vermieden werden. Bei Überschreiten einer Grenze reduziert der Frequenzumrichter seine
Ausgangsfrequenz.
u/f-Kennline, Spannungserhöhung: Da der Frequenzumrichter Spannung und Frequenz dem An-
trieb vorgibt, kann beides beeinflusst werden. In Teilbereichen kann somit die M/n-Kennlinie des
Motor beeinflusst werden. Anwendungen: Losbrechmoment; Spannungsabsenkung bei Schwach-
last, um Geräusch- und Wärmeabgabe zu reduzieren
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

82. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 82 von 108
4 Sonderformen elektrischer Maschinen
Die Funktionsprinzipien der Grundformen (rotierender) elektrischer Maschinen
- Gleichstrommotor mit Kommutator
- Asynchronmaschine
- Synchronmaschine
finden sich in verschiedensten Anwendungen und Bauformen wieder. Besonders die technischen
Fortschritte in der Halbleitertechnik ermöglichen es, preisgünstig aus einer Gleichspannung ein
Drehstromsystem zu erzeugen. Asynchronmaschinen und besonders die Synchronmaschinen wer-
den dadurch in den letzten Jahren mehr und mehr in Anwendungen eingesetzt, die vorher Motoren
mit Kommutator vorbehalten waren.
Es muss angemerkt werden, dass bei vielen Sonderbauformen und besonders bei kleinen Maschi-
nen die für größere Maschinen zulässigen Vernachlässigungen bei der Berechnung nicht erlaubt
sind. Nebeneffekte beeinflussen das Betriebsverhalten maßgeblich, gelegentlich sogar vorwie-
gend.
Im Folgenden werden einige Beispiele verschiedenartiger Bauformen angeführt. Alle Beispiele
lassen sich auf die drei oben angeführten Grundformen zurückführen.
4.1 Schrittmotoren
Einsatzgebiete
- Verpackungsmaschinen
- Textilmaschinen
- Etikettiermaschinen
- Handhabungsgeräte
- Positioniereinrichtungen
- Druckwerke
- Prägemaschinen
- Medizinische Geräte
Die folgende Beschreibung ist einer Firmenschrift der Fa. Betz entnommen:
Der Schrittmotor ist von seinem Aufbau her eine hochpolige Synchronmaschine. Es werden hier
ausschließlich zweiphasige Motoren mit 50 Polpaaren vorgestellt.
Zum Betreiben eines Schrittmotors ist eine Ansteuerung erforderlich, die beim Durchschalten der
Motorphasen ein Drehfeld erzeugt. Diese Elektronik wird über einen Takteingang angesteuert.
Die Größe der Frequenz, die an diesem Takteingang anliegt, bestimmt die Geschwindigkeit des
Motors. Die Anzahl der einzelnen Impulse ist ein Maß für den ausgeführten Drehwinkel also eine
Vorgabe sowohl des Geschwindigkeits- als auch des Positionssollwertes.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

83. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 83 von 108
Grundlagen
Schrittmotoren werden von ihrer Bauart her in zwei Gruppen eingeteilt:
- Permanentmagnetmotoren
- Hybridmotoren
Motorprinzip
Permanentmagnet-Schrittmotoren werden dort eingesetzt, wo nur kleine Drehmomente benötigt
werden. Sie haben in den meisten Fällen einen Schrittwinkel von 7,5° und größer. Für kleinere
Schrittwinkel ist dieser Motortyp, bedingt durch seine Bauart, nicht geeignet. Hier wählt man den
Hybrid-Schrittmotor, der eine Auflösung von 200 Schritten/Umdrehung aufweist, was einen
Schrittwinkel von 1,8° entspricht. Der Schrittwinkel kann durch Ansteuerung im Halbschrittbe-
trieb auf 0,9° (400 Schritte pro Umdrehung) reduziert werden. Noch höhere Auflösungen von bis
zu 2000 Schritten/Umdrehung sind mit dem Microstep-Verfahren möglich. Die Micro-
Schrittwinkel werden rein steuerungstechnisch erzeugt und erfordern lediglich einen Hybrid-
Schrittmotor mit 1,8° Schrittwinkel
.
Abbildung 4.1: Vereinfachte Darstellung eines Schrittmotorrotors
Die Funktionsweise eines Schrittmotors wird aus dem grundsätzlichen Motoraufbau abgeleitet.
Auf der Motorwelle befindet sich ein scheibenförmiger Magnet. Er ist in axialer Richtung so mag-
netisiert, dass sich an der Vorderseite der Nordpol und an der Südseite der Südpol befindet. Über
diesen Magneten stülpen sich von beiden Seiten zwei Schalen aus nicht magnetisiertem Eisen. Zur
Vermeidung von Wirbelstromverlusten sind diese häufig lamelliert ausgeführt. Auf dem Umfang
des Rotorblechpaketes sind gleichmäßig Zähne angeordnet. Das linke Rotorblechpaket ist um ei-
nen halben Zahn gegenüber dem rechten Rotorblechpaket versetzt. Der Stator ist ebenfalls ge-
zahnt. Abhängig davon, ob sich Zahnfuß oder Zahnkopf von Rotor und Stator gegenüberstehen,
ergeben sich verschiedene Luftspalte. Wird eine Phase der Statorwicklung von Gleichstrom
durchflossen, so wird dieser Pol erregt. Der Permanentmagnetrotor dreht sich und richtet sich
dabei entsprechend dem magnetischen Fluss aus. Da die andere Wicklung nicht durchflutet wird,
ist dieser Pol nicht erregt und es findet kein Magnetfluss statt.
Der magnetische Fluss des erregten Pols sucht sich den Weg des kleinsten magnetischen Wider-
standes. Dies ist bei einem Luftspaltminimum der Fall, also dann, wenn sich Rotor- und Stator-
zahn gegenüber stehen. Wird nun die andere Statorwicklung durchflutet, so bewegt sich der Rotor
zum nächsten Luftspaltminimum. Diese Bewegung, die dem Schrittwinkel entspricht, ist abhängig
von der Zähnezahl des Stators.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

84. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 84 von 108
In Abbildung 4.2 ist ein Schrittmotor für einen Tachometer gezeigt (VDO). Die zugehörige E-
lektronik kann die beiden Wicklungen I und II in 32 Stufen mit Strom versorgen, so dass sich der
Rotor des Schrittmotors zwischen 0° und 90° auf 32 Positionen einstellen lässt.
ü = 50 : 1
I
N
II
ΙΙ Ι S
0° 45° 90°
N N
N
6400 S chritte
32 Schritte / 90° ⇒ 4 ⋅ 32 ⋅ 50 =
360° am Zeiger
Abbildung 4.2: Antrieb für einen Autotachometer (VDO), die Schwärzung in dem Schema unten
symbolisiert die Größe des jeweiligen Stromes
4.2 Linearmotoren
Durch Abwicklung des Luftspaltes einer Asynchronmaschine oder Synchronmaschine erhält man
einen Antrieb, der eine translatorische Bewegung ausführt. Beispiel: Der Antrieb des Transrapid
ist eine Synchronmaschine.
Die Fahrbahntrasse enthält die Statorwicklung, die über Stromrichter mit einem „Drehstrom“ ver-
sorgt wird. Im Fahrzeug befindet sich, vergleichbar zum Rotor in einer Synchronmaschine, die
Erregerwicklung, die von einem Gleichstrom durchflossen wird. Die einzelnen Stränge der Sta-
torwicklung müssen mit einer Frequenz angesteuert werden, die der Fahrgeschwindigkeit des Zu-
ges entspricht. Die relative Lage der Pole des Fahrzeugs zum Feld des Stators entspricht dem Pol-
radwinkel bei der Synchronmaschine und bestimmt somit die Vortriebs- oder Bremskraft. Die
Stromrichter längs der Fahrtrasse müssen somit entsprechend der aktuellen Position des Fahrzeugs
angesteuert werden.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

85. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 85 von 108
Das Magnetfeld erzeugt nicht nur eine Vortriebskraft, sondern bewirkt auch durch die gegenseiti-
ge Anziehung der Eisenflächen eine vertikale Kraft, die den Zug zum Schweben bringt. Eine Viel-
zahl kleinerer Magnete sorgt u. a. für eine Regelung in horizontaler Richtung und Stabilisierung in
vertikaler Richtung.
Bild 2: Feld- und Stromverteilung
a) Drehstromwicklung und Erregerteil
b) sinusförmige Anteile des Strombelages A und der Induktion B
Bild 1: Grundsätzliche Anordnung von Stän-
der und Erregerteil mit der Tragkraft Fy und
Schubkraft Fx.
1 Ständer 2 Erregerteil
Bild 10: Energieversorgung der Wicklungsabschnitte.
a) Versorgung langer Wicklungsabschnitte durch jeweils einen Frequenzumformer
b) Frequenzumrichter versorgt nacheinander mehrere verkürzte Wicklungsabschnitte mit Hilfe eines Schaltverteilers
1 Frequenzumformer 2 Schaltverteiler
Abbildung 4.3: Zum Transrapid aus ETZ-A Bd. 96 (1975), H. 3
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

86. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 86 von 108
4.3 Drehstrom-Lichtmaschine für Pkw`s/Lkw`s
Abbildung 4.4: Drehstromlichtmaschine
Die Funktionsweise und der Aufbau entspricht weitgehend dem eines normalen Synchrongenera-
tors mit Schleifringen. Der Rotor ist als „Klauenpolrotor“ gebaut. Diese Bauform ermöglicht eine
hohe Polpaarzahl und eine einfache Herstellung des Rotors. Die Erregerwicklung besteht aus einer
einzigen Spule, die konzentrisch um die Maschinenachse gewickelt ist. Der von der Synchronma-
schine erzeugte Drehstrom wird durch Dioden gleichgerichtet, um damit das Bordnetz zu versor-
gen. Die Bordnetzspannung wird über einen Spannungsregler durch Verstellung des Erregerstro-
mes geregelt.
4.4 Antrieb für einen kleinen Lüfter (z. B. in Rechnern)
Der Stator enthält eine zweiphasige „Drehstrom“-Wicklung mit einer Nut pro Pol, der Stator er-
hält dadurch das Aussehen eines Polrades, wird aber mit Drehstrom versorgt und ist geblecht. Der
außen liegende Rotor ist aus einem Permanentmagneten hergestellt. Der „Drehstrom“ wird aus der
24 V-Gleichspannungsversorgung durch eine Schaltung mit Transistoren erzeugt. Der Motor ist
bei dieser Betrachtungsweise eine Synchronmaschine. Andererseits kann man sich auch einen
permanenterregten Gleichstrommotor vorstellen, bei dem die Welle fest ist und sich das Gehäuse
dreht. Die mechanische Kommutierung der Gleichstrommaschine wird durch die elektronische
Umschaltung ersetzt. Welche der Betrachtungen mehr und welche weniger zutreffend ist, hängt
von der genauen Art der Ansteuerung der Schalttransistoren ab.
Abbildung 4.5: Antrieb für einen kleinen Lüfter (PC)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

87. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 87 von 108
4.5 Autotachometer, Drehzahlmesser usw.
Stellt man sich eine Drehstromasynchronma-
schine vor, die mit Gleichstrom (also einem
„Drehstrom“ mit der Frequenz 0) versorgt
wird, dann stellt sich eine M-n-Kennlinie ein,
die für Drehzahlen kleiner als die Kippdreh-
zahl ein drehzahlproportionales Moment auf-
weist.
Das stationäre Feld des Ständers kann auch
durch einen Permanentmagneten erzeugt wer-
den. Gestaltet man nun den Rotor als „Käfig-
läufer“ mit unendlich vielen Stäben und ver-
tauscht Ständer und Rotor, dann übt der nun
rotierende Permanentmagnet ein Drehmoment
auf den feststehenden Teil aus, das der Dreh-
zahl proportional ist. Ein Tachometer der dar-
gestellten Bauart ist also im Kern eine Asyn-
chronmaschine.
Abbildung 4.6: Prinzip eines mechanischen Autotachometers und Analogie zu einer Asyn-
chronmaschine
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

88. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 88 von 108
4.6 Scheibenmotor
Aus einer Firmenschrift der Fa. Dual (um 1972):
Bei dem speziell für den HiFi-Plattenspieler Dual 701 entwickelten Zentralantrieb Dual EDS
1000 handelt es sich um einen langsam laufenden, kollektorlosen Gleichstrom-Elektronik-Motor,
der seine Energie aus einem stabilisierten Netzteil bezieht.
Die bei Gleichstrom-Motoren üblicherweise vom Kollektor vorgenommene mechanisch-
elektrische Umschaltung (Kommutierung) wird beim Dual EDS 1000 von zwei Hall-Generatoren
elektronisch gesteuert. Diese Hall-Generatoren steuern – in Abhängigkeit von der Rotorsteuerung
– über vier Schalttransistoren nacheinander vier Wicklungsstränge des Motors.
Das zyklische Schalten der Wicklungsstränge bzw. Feldspulen bewirkt ein Drehfeld und damit
eine Drehbewegung des Rotors. In den jeweils nicht angesteuerten Feldspulen wird gleichzeitig
eine drehzahlproportionale Spannung induziert, deren Größe mit einer separat erzeugten konstan-
ten Spannung verglichen wird. Die Spannungsdifferenz steuert den Stromfluss in den vier Schalt-
transistoren so exakt, dass kurzzeitige Drehzahlabweichungen des Motors kleiner als 0,025 %
bleiben.
Der Rotor des Dual EDS 1000 ist nutenlos und hat einen mitlaufenden magnetischen Rückschluss.
Die Feldspulen des Motors sind eisenlos und ortsfest im Luftspalt zwischen dem achtpoligen
Ringmagnet des Rotors und dem magnetischen Rückschluss angeordnet. Daraus resultieren die
gravierenden Vorteile des Dual EDS 1000:
Ohne Polfühligkeit bzw. Polrucken, Hysterese- oder Wirbelstromverluste und ohne störende Nu-
tenfrequenzen garantiert der Dual EDS 1000 den völlig vibrationsfreien und gleichförmigen An-
trieb es HiFi-Plattenspielers Dual 701.
Abbildung 4.7: Direktantrieb eines Plattenspielers als Beispiel für einen elektronischen Gleich-
strommotor
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

89. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 89 von 108
5 Zur Berechnung des dynamischen Verhaltens von Drehfeldmaschinen
5.1 Voraussetzungen
Es wird wie üblich angenommen, dass das Luftspaltfeld sinusförmig ist, dass keine Sättigung vor-
kommt und dass es keine Eisenverluste gibt. Die folgenden Verfahren ermöglichen es, beliebige
dynamische Vorgänge zu berechnen, also insbesondere Anlaufvorgänge und Ausgleichsvorgänge
bei einer Änderung der Belastung oder Änderung der Netzspannung. Die Netzspannung und die
Ströme brauchen nicht sinusförmig zu sein, es wird lediglich vorausgesetzt, dass die Summe der
Ströme in den 3 Strängen der Maschine immer 0 ist. Bei Maschinen, deren Stränge im Y geschal-
tet sind, ist das immer gegeben. (Bei Dreiecksschaltung ist das nicht zwangsläufig der Fall, aber
durch den Aufbau der Wicklung wird immer erreicht, dass ein gegebenenfalls verbleibender
Summenstrom keine Auswirkungen hat.)
Alle Gleichungen können auch in normierter Form angegeben werden.
5.2 Idee der Berechnungsweise
Für Ausgleichsvorgänge reicht es nicht aus, Rechnungen mit einem einphasigen Ersatzschaltbild
durchzuführen, es sei denn, die untersuchten mechanischen Vorgänge verlaufen sehr viel langsa-
mer als die magnetischen Vorgänge in der Maschinen. Deshalb müssen die Gleichungen für alle
Stränge der Maschine aufgestellt werden, wobei es intensive Kopplungen zwischen den Strängen
und zwischen den Strängen und den Wicklungen des Rotors gibt.
Der Rotor einer Synchronmaschinen ist immer unsymmetrisch und die Erregerwicklung wirkt
immer nur in einer Achse. Aus Sicht einer Statorspule ändert sich also der magnetische Wider-
stand des Eisenkreises zweimal pro Rotordrehung. Deshalb sind die Gleichungen aus Sicht des
Stators recht verwickelt. Daraus resultiert nun die Idee, die Gleichungen für ein Koordinatensys-
tem aufzustellen, dessen eine Achse in jedem betrachteten Zeitpunkt in die Richtung des Erreger-
feldes zeigt und dessen zweite Achse senkrecht dazu verläuft. Da dieses neue Koordinatensystem
für jeden betrachteten Zeitpunkt neu auf die momentane Lage des Rotors eingestellt wird, ist die
Asymmetrie des Rotors nicht mehr zeitlich veränderlich. Es zeigt sich, dass dadurch alle Glei-
chungen erheblich vereinfacht werden. Zusätzlich hat eine Beschreibung in diesem Koordinaten-
system den Vorteil, dass im stationären Betrieb keine zeitlich veränderlichen Größen mehr auftre-
ten; die gleichmäßige Rotation des Rotors und des Feldes ist in dem gewählten Bezugssystem
nicht mehr vorhanden. Die Transformation aller Größen in dieses besondere Koordinatensystem
wird Park'sche Transformation genannt, die resultierenden Gleichungen zur Beschreibung der
Synchronmaschine werden Park'sche Gleichungen genannt. Von verschiedenen früheren Ansätzen
der beschriebenen Art hat sich die Vorgehensweise von Park als besonders vorteilhaft erwiesen.
Da Asynchronmaschinen einen symmetrischen Läufer haben und der Läufer auch nicht synchron
mit dem Drehfeld umläuft, bietet hier die Park'sche Transformation zunächst keinen offensichtli-
chen Vorteil. Bei numerischen Rechnungen (Simulationen) kann durch die Anwendung der Park'-
schen Transformation jedoch eine erhebliche Rechenzeitverkürzung erreicht werden, da ja nur
noch Vorgänge im Bereich der Schlupffrequenz berechnet werden müssen während die netzfre-
quenten Vorgänge durch die Transformation nicht mehr vorhanden sind.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

90. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 90 von 108
5.3 1. Schritt: Transformation auf ein 2-phasiges a-b-System
Das Drehfeld in der Maschine wird durch 3 Stränge erzeugt:
bg bg
b1 ( x , t ) = B1 i1 ⋅ cos x
bg b
b2 ( x , t ) = B2 i2 ⋅ cos x − 2 3π g
b3 ( x , t ) = B3 bi3 g ⋅ cosb x + 2 3π g (5.1)
also
b g b g b g
b( x , t ) = b1 x , t + b2 x , t + b3 x , t
Da die 3 Stränge gleichartig aufgebaut sind und die Summe der Ströme gleich 0 ist, ist das Feld
bereits durch 2 der Ströme eindeutig bestimmt. Man kann deshalb für diese Bedingungen jedes
beliebige Feld in der Maschine alleine auch durch 2 geeignet aufgebaute Stränge erzeugen.
Zweckmäßig sind 2 Stränge a und b, die um 90° gegeneinander versetzt sind. Willkürlich wird der
Strang a in die gleiche Richtung gelegt wie der Strang 1:
b g bg
ba ( x , t ) = Ba ia ⋅ cos x
bb ( x , t ) = Bb bib g ⋅ cosb x − π / 2g (5.2)
b( x , t ) = ba b x , t g + bb b x , t g
Man kann einfach nachrechnen, dass mit Ba, Bb nach folgender Gleichung die Felder des 3-
strängigen Systems und des 2-stränginge Systems identisch sind:
LM 2 −
1 2
−
1 2 OP
LM Ba OP 3 M
M3 2 3
1
2 3
1
B1 PP LM OP
MM Bb PP = ⋅ 0
2 M
− • B2
PP MM PP (5.3)
N B0 Q MM 1 1
2
1
2
B3
PQ N Q
N3 3 3
oder in Umkehrung
LM 2 0
1OP
LM B1 OP M 3
2 M 1 2 1 1
3PP Ba LM OP
MM B2 PP = 3 M 2 3 PP MM PP
⋅ − • Bb (5.4)
N B3 Q MM 1 2 2
1 1
3
PP
B0 N Q
MN− 2 3 −
2 3 Q
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

91. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 91 von 108
In Matrizenform ist das kürzer:
B ab0 = k B ⋅ A ⋅ B 123
1 (5.5)
B 123 = ⋅ A −1 ⋅ B ab0
kB
Die Matrix A ist so normiert, dass A-1=A' ist. Die Nullkomponente muss natürlich immer 0 sein,
sie ist hier nur der Vollständigkeit halber mit aufgenommen, mit dem Vorteil, dass die Transfor-
mationsmatrix quadratisch ist.
Da Ba über das Durchflutungsgesetz unmittelbar mit ia verbunden ist und über das Induktionsge-
setz unmittelbar mit ua, gelten für die Ströme und Spannungen entsprechende Transformationen
mit der gleichen oben angegebenen Matrix A:
Iab0 = k I ⋅ A ⋅ I123
(5.6)
U ab0 = kU ⋅ A ⋅ U 123
Die Faktoren kU und kI sind frei wählbar, kB ist nur von Bedeutung, wenn die Feldgrößen in der
Maschine berechnet werden sollen und wird im Folgenden nicht weiter berücksichtigt. Für die
Wahl von kU und kI gibt es folgende günstige Alternativen:
a) kU = kI = 1: (5.7)
Die Ströme und Spannungen in beiden Systemen sind in folgenden Sinn gleich:
2 2 2 2 2 2
ua + ub + u0 = u1 + u2 + u3 (5.8)
(i0=0, bzw. u0=0 wie oben dargestellt). Die "Länge der Vektoren" Uab0 und U123 sind also gleich.
Für den typischen Fall einer symmetrischen Anlage sind die Impedanzen der a-b-Maschine gleich
den Impedanzen der 1-2-3-Maschine, müssen also nicht umgerechnet werden:
X a = X b = X1 = X 2 = X 3 (5.9)
Außerdem ist wegen
I'ab0 ⋅ U ab0 = I123 ⋅ U123
'
(ia ⋅ ua + ib ⋅ ub + i0 ⋅ u0 = i1 ⋅ u1 + i2 ⋅ u2 + i3 ⋅ u3 ) (5.10)
die Transformation leistungsinvariant und somit ist auch das Drehmoment beider Maschinen
gleich.
2
b) kU = k I = (5.11)
3
Die Impedanzen bleiben wie bei a) unmittelbar übertragbar. Außerdem ist aber auch (bei u0=0 und
i0=0) vorteilhaft
ua = u1 und ia = i1 (5.12)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

92. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 92 von 108
Demgegenüber steht der Nachteil, dass für Leistungen und Drehmomente gilt:
2
Pab0 = kU ⋅ k I ⋅ P =
123 ⋅P123
3
und entsprechend für das Drehmoment. Je nach zu untersuchender Fragestellung kann a) oder b)
oder auch eine andere Wahl zweckmäßig sein.
5.4 Besonderheiten bei der Rechnung in normierten Größen
Oft werden Ströme und Spannungen auf Normierungsgrößen bezogen:
U * = U/UNorm
I* = I/INorm
Für die Leistung ist die Scheinleistung der gesamten Maschine als Normierungsgröße üblich:
P* = P/SNorm
Im Normpunkt ist dann U* = 1, I* = 1, S* = 1, P* = cos ϕ.
Da die Strangzahl in der Normierungsgröße enthalten ist, ist
S* = U* ⋅ I*
Mit Bezug des Drehmomentes auf die synchrone mechanische Drehzahl ist
M* = P*
Bei dem Übergang von dem 123-System in das abo-System gibt es nun zwei Möglichkeiten:
Die Normierungsgrößen werden nicht transformiert: Dann sind alle Gleichungen (z. B. Gleichung
5.10) einfach um die Normierungsgrößen erweitert. Als Nachteil ist anzusehen, dass im Norm-
punkt die Größen in abo-System nicht 1 sein müssen (abhängig von den gewählten kU, kI).
Es werden neue Normierungsgrößen für das abo-System festgelegt, sodass für den Normpunkt
wieder U* = 1, I* = 1, S* = 1 ist. (Das gilt nur für a – b, die Komponenten „0“ sind immer null.)
5.5 2. Schritt: Transformation von a-b in ein verdrehtes x-y-System
Die a-b-Maschine wird in einem 2. Schritt durch eine x-y-Maschine ersetzt. Die Stränge x und y
stehen senkrecht aufeinander und x-y ist gegen a-b um einen Winkel γ verdreht. (Der Übersicht-
lichkeit halber wird hier nur der Fall der Polpaarzahl 1 betrachtet.)
Mit folgender Umrechnung ist das durch x-y erzeugte Feld ist identisch dem durch a-b erzeugten
Feld:
⎡ bx ⎤ ⎡ cos γ sin γ ⎤ ⎡ba ⎤
⎢b ⎥ = ⎢ •
cos γ ⎥ ⎢bb ⎥
(5.13)
⎣ y ⎦ ⎣ − sin γ ⎦ ⎣ ⎦
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

93. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 93 von 108
Oder wieder kürzer in Matrizenform:
B xy = D ⋅ Bab
Wie oben ist D-1 = D'.
Für die Ströme und Spannungen gilt entsprechendes:
U xy = D ⋅ U ab
I xy = D ⋅ I ab
Da sich bei dem Übergang von a-b auf x-y die Anzahl der Stränge nicht geändert hat, sonders es
sich um eine reine Drehung handelt, sind die Widerstände und Leistungen unverändert.
5.6 3. Schritt: Die Gleichungen der Synchronmaschine
Folgende Spulen werden berücksichtigt:
Index
d Statorspule in d-Richtung
q Statorspule in q-Richtung
F Erregerspule
D Dämpferkäfig in d-Richtung
Q Dämpferkäfig in q-Richtung
dD Gegeninduktivität zwischen d und D
... usw. für alle Spulenpaarungen
γ wird so gewählt, das der Strang x für den betrachteten Augenblick mit der Längsachse des Ro-
tors (die Achse des Erregerfeldes) zusammen fällt, y senkrecht dazu steht, es wird dann d-q statt x-
y . benutzt. (Abbildung)
d-Achse: Längsachse (direct axis)
q-Achse: Querachse
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

94. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 94 von 108
Alle Wicklungen haben einen ohmschen Widerstand und eine Induktivität. Die induzierten Span-
nungen z. B. für die Spule d ergibt sich aus der Änderung des magnetischen Flusses Ψd in der
Spule d:
dΨd
udi =
dt
Dabei muss berücksichtigt werden, dass die Transformation Udq = D ⋅ Uab keine Auswirkung auf
das Induktionsgesetz hat. Die Spannung Udq ist an einem Spulenpaar messbar, dass gegenüber a –
b um den Winkel γ verdreht ist, aber im Stator ruhend ist. Deshalb setzt sich die gesamte Flussän-
derung aus 2 Anteilen zusammen: Zum einen bewirkt jede Stromänderung in einer der Spulen d,
D und f (wie bei einem Transformator) eine Flussänderung und induziert eine Spannung, die an
der rotierenden Spule gemessen werden könnte:
di di di
udi −1 = Ld ⋅ d + LdD ⋅ D + LdF ⋅ F
dt dt dt
Zum Anderen bewirkt in der ruhenden Spule die Drehung des Feldes eine zusätzliche Flussände-
rung. Ein im Betrachtungszeitpunkt vorhandener Fluss in Querrichtung Φquer würde mit fortschrei-
tender Drehung x des Rotors - da die d-Spule feststeht - in der Spule d einen Fluss in der Art
Ψd = − Φ quer ⋅ sin x
erzeugen. Die resultierende Flussänderung ist somit (ohne Berücksichtigung der Windungszahlen)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

95. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 95 von 108
dΨd dx dγ
= − ⋅ Φ quer = − ⋅ Φ quer
dt dt dt
(Die Änderung des Flusses dΦquer /dt erzeugt keine Spannung, weil Φquer in dem Betrachtungszeit-
punkt senkrecht zur d-Achse steht und somit nicht mit Spule d verkoppelt ist.) Der mit dem Stator
verbundene Fluss Φquer ergibt sich aus den Induktivitäten und Gegeninduktivitäten:
Φ quer = Lq ⋅ iq + LqQ ⋅ iQ
Somit ist die insgesamt in der Spule d induzierte Spannung:
di
dt
di
dt
di
udi = Ld ⋅ d + LdD ⋅ D + LdF ⋅ F − γ ⋅ Lq ⋅ iq + LqQ ⋅ iQ
dt
d i
Entsprechend wird für die übrigen Spulen verfahren und unter Berücksichtigung der ohmschen
Widerstände ergibt sich schließlich folgendes Gleichungssystem:
LM Ld 0 LdF LdD 0 OP
id udLM OP LM OP LM
Rd ⋅ id − γ ⋅ Lq ⋅ iq + LqQ ⋅ iQ d i OP
MM L0 Lq 0 0 LqQ
PP
iq uq MM PP MM PP MM
Rq ⋅ iq + γ ⋅ Ld ⋅ id + LdD ⋅ i D + LdF ⋅ i Fb gP
0 • i F = uF − RF ⋅ i F
MM PP (5.14)
MM LdD
dF 0
0
LF
LDF
LDF
LD 0 iD
PP 0
MM PP MM PP
RD ⋅ i D PP
MN 0 LqQ 0 0 LQ iQ PQ 0 MN PQ MN PQ
RQ ⋅ iQ NM Q
Die Vorzeichen sind dabei so gewählt, dass im stationären Motorbetrieb alle Ströme und Span-
nungen positiv sind. (Verbraucherzählpfeilsystem).
Für praktische Rechnungen ist es sehr vorteilhaft, dass die Matrix der Induktivitäten konstant ist,
sodass sie nur einmalig aufgestellt und invertiert werden muss, um dann die Ableitungen der
Ströme ausrechnen zu können.
Das Drehmoment kann aus der Leistung ermittelt werden, die aus der durch die Drehung mit dγ/dt
erzeugten Spannung bewirkt wird, also entnimmt man der rechten Seite des Gleichungssystems:
pmech = ud ⋅ id + uq ⋅ Iq – Rd ⋅ i d – Rq ⋅ i q
2 2
d i b
m = − Lq ⋅ iq + LqQ ⋅ iQ ⋅ id + Ld ⋅ id + LdD ⋅ i D + LdF ⋅ i F ⋅ i q g (5.15)
(Dies ist das Moment der 2-poligen d-q-Maschine; die Umrechnung auf die reale 1-2-3-Maschine
erfolgt mit den oben angegebenen Faktoren unter Berücksichtigung der Polpaarzahl.)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

96. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 96 von 108
5.7 Anwendung auf die Asynchronmaschine
Es entfällt die Erregerwicklung und die Maschine ist vollständig symmetrisch. Da der Läufer nicht
synchron rotiert, sind verschiedene Alternativen für die Wahl von x-y üblich. Bei beliebiger Wahl
des x-y-Systems wird in Analogie zu γ der Winkel ρ als der Winkel zwischen einem Bezugspunkt
des Rotors und der x-Achse definiert. Der mechanische Drehwinkel des Rotors ist: ϕm = γ - ρ.
Index 1 bezeichnet alle Größen des Ständers und 2 alle Größen des Läufers. Aus dem System
(5.14) wird dann:
⎡ψ 1x ⎤ ⎡ L1 0 Lh 0 ⎤ ⎡ i1x ⎤ ⎡ u1x ⎤ ⎡ R1 ⋅ i1x − γ ⋅ ( L1 ⋅ i1 y + Lh ⋅ i2 y ) ⎤
⎢ψ ⎥ ⎢ ⎢ ⎥ ⎢ ⎥
⎢ 1y ⎥ = ⎢ 0 L1 0 Lh ⎥ ⎢ i1 y ⎥ ⎢u1 y ⎥ ⎢ R1 ⋅ i1 y + γ ⋅ ( L1 ⋅ i1x + Lh ⋅ i2 x ) ⎥
⎥• = ⎢ ⎥−⎢ ⎥ (5.16)
⎢ψ 2 x ⎥ ⎢ Lh 0 L2 0 ⎥ ⎢ i2 x ⎥ ⎢ 0 ⎥ ⎢ R2 ⋅ i2 x − ρ ⋅ ( L2 ⋅ i2 y + Lh ⋅ i1 y ) ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣ψ 2 y ⎦ ⎣ 0
⎢ ⎥ ⎢ Lh 0 L2 ⎦ ⎣i2 y ⎦ ⎣ 0 ⎦ ⎢ R ⋅ i + ρ ⋅ ( L ⋅ i + L ⋅ i ) ⎥
⎥ ⎢ ⎥ ⎢ 2 2y
⎣ 2 2x h 1x ⎥ ⎦
Entsprechend ergibt sich für das Drehmoment
m = − ( L1 ⋅ i1 y + Lh ⋅ i2 y ) ⋅ i1x + ( L1 ⋅ i1x + Lh ⋅ i2 x ) ⋅ i1 y (5.17)
Die Flüsse sind:
ψ 1x = L1 ⋅ i1x + Lh ⋅ i 2 x
ψ 1 y = L1 ⋅ i1 y + Lh ⋅ i 2 y
(5.18)
ψ 2 x = L2 ⋅ i2 x + Lh ⋅ i 1x
ψ 2 y = L2 ⋅ i2 y + Lh ⋅ i 1 y
Entsprechend kann das Drehmoment auch durch die Flüsse ausgedrückt werden:
m = −ψ 1 y ⋅ i1x + ψ 1x ⋅ i1 y
(5.19)
m = ψ 2 y ⋅ i2 x − ψ 2 x ⋅ i2 y
Besonders übersichtlich werden die Zusammengänge, wenn man γ so wählt, das x in Richtung des
Läuferflusses liegt, dass also ψ2y = 0 ist.
Dann gilt:
L
i2 y = − h ⋅ i1 y (5.20)
L2
L
m = ψ 2 x ⋅ h ⋅ i1 y (5.21)
L2
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

97. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 97 von 108
Ermittelt man aus den letzten beiden Gleichungen aus (5.16) die Größen i2x und i2y als Funktio-
nen der Flussverkettungen und deren Ableitungen und setzt man diese in (5.18) für ψ2x ein, dann
folgt::
ψ 2 x + T2 ⋅ψ 2 x
i1x =
Lh
(5.22)
L2
T2 = (Läuferzeitkonstante)
R2
Gleichung (5.21) entspricht der einer fremderregten Gleichstrommaschine: i1x erzeugt nach Glei-
chung (5.22) ein Feld und i1y entspricht dem Ankerstrom. Diese Transformation wird heute zur
Regelung von Frequenzumrichtern eingesetzt (feldorientierte Regelung, Vektorregelung).
Gelegentlich ist es übersichtlicher, wenn statt mit den Strömen mit den Flussverkettungen gerech-
net wird:
⎡ 1 1 Lh ⎤
⎢ σT −γ − ⋅ 0 ⎥
σ T1 L2
⎢ 1
⎥
⎡ψ 1x ⎤ ⎡ u1x ⎤ ⎢ 1 1 Lh ⎥ ⎡ψ 1x ⎤
⎢ψ ⎥ ⎢ ⎥ ⎢ γ − ⋅
σ T1 L2 ⎥ ⎢ψ 1 y ⎥
0
⎢ 1 y ⎥ = ⎢u1 y ⎥ − ⎢ σ T1 ⎥•⎢ ⎥ (5.23)
⎢ψ 2 x ⎥ ⎢ 0 ⎥ ⎢ 1 Lh 1 ⎥ ⎢ψ 2 x ⎥
⎢ ⎥ ⎢ ⎥ ⎢− ⋅ 0 −ρ ⎥ ⎢ ⎥
⎢ψ 2 y ⎥ ⎣ 0 ⎦ ⎢ σ T2 L1
⎣ ⎦ σ T2 ⎥ ⎢ψ 2 y ⎥
⎣ ⎦
⎢ 1 Lh 1 ⎥
⎢ 0 − ⋅ ρ ⎥
⎢
⎣ σ T2 L1 σ T2 ⎥ ⎦
LL −L 2
σ = 1 2 h (totaler Streukoeffizient)
L1 L2
(5.24)
L
T1 = 1 (Ständerzeitkonstante)
R1
L2
T2 = (Läuferzeitkonstante)
R2
Das Drehmoment kann ebenfalls durch die Flüsse ausgedrückt werden:
ψ1y ⎛ L ⎞ ψ ⎛ L ⎞
m=− ⋅ ⎜ψ 1x − h ⋅ψ 2 x ⎟ + 1x ⋅ ⎜ψ 1 y − h ⋅ψ 2 y ⎟
σ L1 ⎝ L2 ⎠ σ L1 ⎝ L2 ⎠ (5.25)
m = − h ⋅ (ψ 1x ⋅ψ 2 y − ψ 1 y ⋅ψ 2 x )
L
σ L1 L2
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

98. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 98 von 108
6 Übungsaufgaben
6.1 Allgemeines, Grundlagen
Aufgabe GET 1 (Drehspulmessgerät, Kraft/Drehmoment im Magnetfeld)
Gegeben ist ein Drehspulmessgerät, dessen Drehspule wie üblich durch eine Rückstellfeder bei I =
0 A in einer bestimmte Anfangsstellung gehalten wird.
b
B0
Südpol
I
. Nordpol
a
1. Geben Sie die Richtung des Drehmoments bei Stromfluss in der eingezeichneten Richtung an!
2. Berechnen Sie allgemein die Abhängigkeit des Drehmoments vom Strom M = f(I) der Spule
mit n Windungen!
3. Berechnen Sie die Windungszahl, wenn das Rückstellmoment Mmax der Rückstellfeder bei
Endausschlag bekannt ist und der Maximalstrom Imax, sowie die Felddichte B0 gegeben sind!
4. Für die folgenden Betrachtungen soll die Drehspule mit konstanter Winkelgeschwindigkeit
drehen (keine Rückstellfeder) und an den offenen Klemmen der Drehspule soll die induzierte
Spannung gemessen werden. Tragen Sie qualitativ den Verlauf a) des durch die Spulenfläche
dringenden Flusses und b) der induzierten Spannung über die Winkelstellung der Drehspule
auf.
Zahlenwerte: Imax = 10 mA; B0 = 1 Vs/m2; a = 2 cm; b = 2,5 cm;
Mmax = 10-2 Ncm.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

99. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 99 von 108
Aufgabe GET 2 (Elektrokran, Durchflutung, Kraft)
Der Elektrokran auf einem Autofriedhof hebt die Schrottfahrzeuge mit Hilfe eines runden Topf-
magneten gemäß untenstehender Skizze. Die Abmessungen sind: d1 = 30 cm, d2 = 40 cm, d3 =
50 cm. Durch Lackschicht und Verschmutzung der Fahrzeuge kann mit einer Luftspaltlänge
δ = 1 mm gerechnet werden. Welche elektrische Durchflutung θ muß die Spulenwicklung erzeu-
gen, damit der Magnet eine Tragkraft von F = 20000 N aufbringt? Die magnetischen Widerstände
des Eisens sind für die Berechnung zu vernachlässigen.
6.2 Gleichstrommaschine
Aufgabe GM 1 (Fremderregter Gleichstrommotor)
Ein fremderregter Gleichstrommotor habe folgende Nenndaten:
Nennleistung Pn: 600 kW;
Nennspannung Un: 440 V;
Nenndrehzahl nn: 900 min-1;
Nennerregerstrom Ifn: 50 A;
Nennerregerspannung Ufn: 220 V;
Ankerverluste im Nennbetrieb PAVn 20 kW
Es sollen nur die Verluste durch den Ankerwiderstand und den Erregerwiderstand berücksichtigt
werden.
Eisensättigung und Ankerrückwirkung sollen vernachlässigt werden.
1. a.) Wie groß sind der Widerstand der Erregerwicklung und die Verlustleistung bei Nennbetrieb
in der Erregerwicklung?
b.) Wie groß sind die vom Ankerkreis aufgenommene Leistung, der Nennstrom und der
Ankerwiderstand?
c.) Wie groß sind Nenndrehmoment und die Leerlaufdrehzahl des Motors?
2. Welchen Wert muss die Erregerspannung haben, damit sich bei Nennstrom im Anker eine
Drehzahl von 1500 min-1 ergibt? Wie groß ist das Drehmoment?
3. Wie sind Erreger- und Ankerspannung einzustellen, damit bei 400 min-1 und Nennstrom das
Nenndrehmoment abgegeben wird ?
4. Wie groß muss ein Vorwiderstand im Ankerkreis sein, damit die Maschine bei Nennerregung
und Nennspannung das doppelte Nennmoment als Anfahrmoment entwickelt?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

100. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 100 von 108
Aufgabe GM 2 (Fremderregte Gleichstrommaschine)
Gegeben sind die Daten eines fremderregten Gleichstrommotors:
Nennleistung Pn = 10 kW,
Nenndrehzahl nn = 1500 min-1,
Nennankerspannung UAn = 220 V,
Ankerwiderstand RA = 0,4 Ω.
Die Sättigung sowie Eisen- und Reibungsverluste sind zu vernachlässigen. Bestimmen Sie:
1. das Nennmoment,
2. den Nennstrom,
3. kφn,
4. Die Leerlaufdrehzahl n0,
5. die Kennlinie n/n0 = f (MA/MAn) für φ = φn und φ = φn/2.
Aufgabe GM 3 (Fremderregte Gleichstrommaschine)
Ein Gleichstrommotor mit Fremderregung hat folgende Nenndaten:
Pn = 25 kW; Un = 440 V; nn = 1350 min-1; Ifn = 5 A
Außerdem sind der Gesamtwirkungsgrad im Nennbetrieb und der Widerstand der Erregerwick-
lung bekannt:
ηn = 0,88; Rf = 40 Ω.
Die mechanischen Verluste können wie alle anderen Verluste (außer den Kupferverlusten) ver-
nachlässigt werden.
Die Eisensättigung wird vereinfacht berücksichtigt: Bis zum Nennfluss steigt der Fluss proportio-
nal mit dem Strom (keine Sättigung) und darüber hinaus ist keine Flusserhöhung möglich (Insge-
samt gilt also dass Φ > Φn unmöglich ist!).
1. Bestimmen Sie den Ankernennstrom IAn, den Ankerwiderstand RA und die Leerlaufdrehzahl n0
bei Nennerregung!
2. Der Motor wird mit veränderlicher Spannung betrieben. Er hat die Drehzahl von 850 min-1 und
wird dabei kurzzeitig mit 1,2 ⋅ Mn belastet. Wie groß sind hierbei der Erregerstrom If , der An-
kerstrom IA und die Ankerspannung UA?
3. Bei einer Drehzahl von 2500 min-1 wird die Maschine mit dem höchstzulässigen Moment in
diesem Betriebspunkt im Dauerbetrieb belastet. Dabei ist zu beachten, dass aus konstruktiven
Gründen U > Un und IA > IAN unzulässig sind! Geben Sie die Ankerspannung UA, den Anker-
strom IA und den Erregerstrom If an!
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

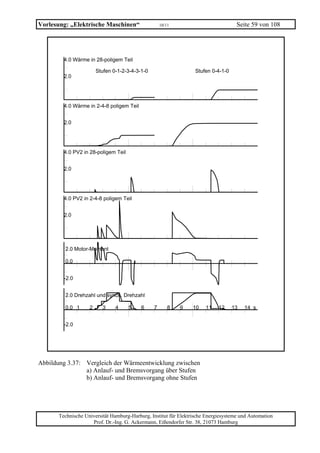
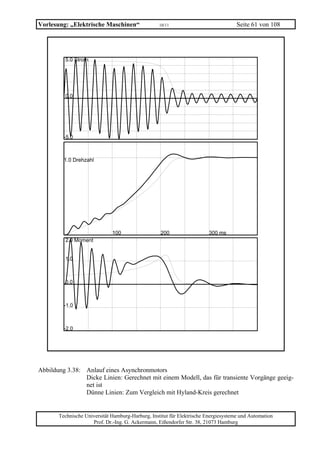
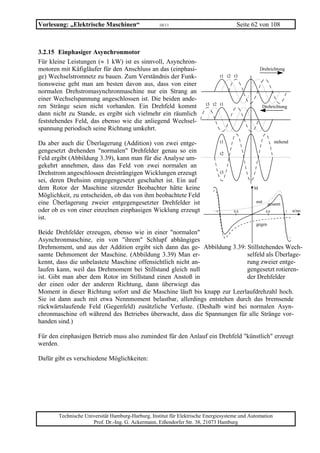
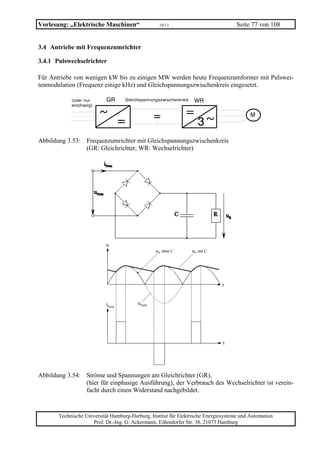
101. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 101 von 108
Aufgabe GM 4 (Nebenschlussmotor)
Ein Gleichstromnebenschlussmotor besitzt die folgenden Daten:
Pn = 150 kW; Un = 500 V; In = 325 A; Ra = 0,05 Ω; nn = 1600 min-1;
Ifn = 5 A; Ufn = 500 V.
Bürstenübergangswiderstände werden vernachlässigt. Eisensättigung wird vernachlässigt, d.h.
Maschinenfluss und Erregerstrom sind einander proportional.
Es gibt in der Maschine Reibungs- und Lüfterverluste.
1. Zeichnen Sie das elektrische Ersatzschaltbild und berechnen Sie den Widerstand der Erreger-
wicklung.
2. Berechnen Sie im Nennpunkt
a.) das Drehmoment an der Welle,
b.) die induzierte Spannung,
c.) kφ, sowie
d.) die Verluste in Anker- und Erregerwicklung und
e.) den Wirkungsgrad.
3. Welche Leerlaufdrehzahl ergibt sich bei Nennspannung und bei halber Nennspannung?
4. Welche Drehzahlen ergeben sich bei Belastung mit Nenndrehmoment und Speisung
a) mit Nennspannung
b) mit halber Nennspannung?
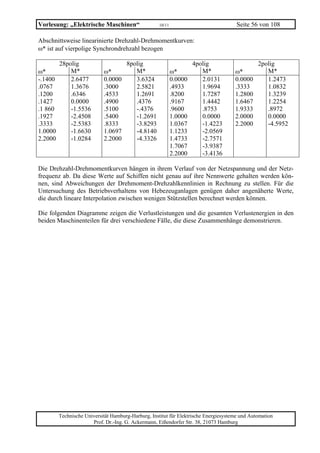
5. Zeichnen Sie das Kennlinienfeld der Maschine im 1. Quadranten.
Aufgabe GM 5 (Reihenschlussmaschine, Sättigung, Messung: Drehmoment-Ankerstrom )
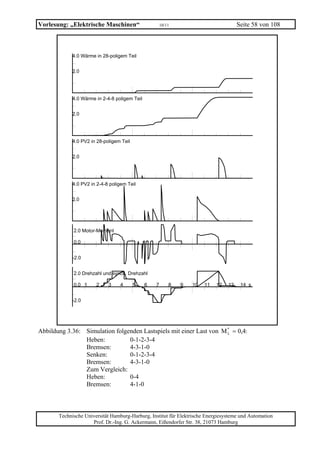
An einer Gleichstromreihenschlussmaschine (Un = 600 V; nn = 1000 min-1; In = 180 A) wurde im
Prüffeld folgender Zusammenhang zwischen Drehmoment und Ankerstrom gemessen:
M [Nm] 36,3 145,2 323,7 907,4 1294,9 1491
I [A] 30 60 90 180 240 270
Bei Nennstrom betragen die Erregerverluste 4 kW. Ankerrückwirkung, Eisen- und mechanische
Verluste sind zu vernachlässigen.
1. Wie groß sind die Nennleistung und der Wirkungsgrad im Nennbetrieb? Welche Werte ergeben
sich für die Widerstände der Erreger- und Ankerwicklung?
2. Berechnen Sie die Drehzahl bei Nennspannung und Nennstrom, wenn der Erregerwicklung ein
Widerstand RP von der halben Größe des Erregerwiderstandes parallelgeschaltet wird!
3. Der Maschine wird (ohne den Parallelwiderstand RP) bei Nennspannung ein Widerstand RS =
0,5 Ω vorgeschaltet. Wie groß ist die Drehzahl bei einem Ankerstrom von 240 A?
4. Die Maschine soll bei Widerstandsbremsung (sie wird vom Netz getrennt, die Erregerwicklung
wird umgepolt und die Maschine auf einen ohmschen Widerstand geschaltet) und einer Dreh-
zahl von 500 min-1 ein Bremsmoment von 1491 Nm entwickeln. Wie groß muss der ange-
schlossene Widerstand sein?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

102. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 102 von 108
Aufgabe GM 6 (Gleichstrommaschine, Messung: Ankerspannung-Erregerstrom)
Eine Gleichstrommaschine wird als fremderregte Maschine geschaltet und mit 900 min-1 angetrie-
ben. Im Leerlauf ergibt sich dann folgender Zusammenhang zwischen der Ankerspannung und
dem Erregerstrom:
UA [V] 0 50 100 150 200 250
If [A] 0 0,4 0,8 1,4 2,2 4
Der Ankerwiderstand der Maschine beträgt 0,125 Ω, der Widerstand der Erregerwicklung 104,55
Ω.
Die Reibungs- und Eisenverluste werden vernachlässigt.
Gesucht werden jeweils:
a) Drehmoment,
b) Drehzahl und
c) mechanische Leistung
bei einem Ankerstrom von 80 A für den Betrieb als:
1. Nebenschlussmotor (UNetz = 230V);
2. Nebenschlussmotor (UNetz = 230V) mit einem Vorwiderstand RfV = 183 Ω im Erregerkreis;
3. fremderregter Motor mit If = 2,2 A und UNetz = 130 V.
Hinweis: Zeichnen Sie zur Berechnung ein Ersatzschaltbild!
6.3 Asynchronmaschine
Aufgabe AsyM 1 (Schleifringläufer, Kipppunkt, Läuferwiderstand)
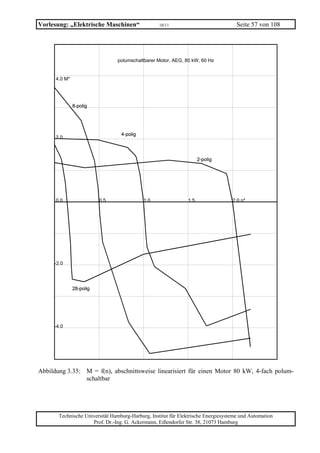
An einem Asynchronmotor mit Schleifringläufer (Ständer und Läufer Y-Schaltung) und zwei Pol-
paaren (p = 2) und mit der Nennspannung:
Un = 660 V fn = 50 Hz
ergeben sich folgende Messwerte:
1) Leerlauf (Synchrondrehzahl) bei Nennspannung und Nennfrequenz:
Ständerstrom I0 = 40 A
2) Kurzschluss (Stillstand) bei Nennfrequenz und einer Ständerspannung von U = 130 V:
a.) Ständerstrom I1A = 120 A;
cosϕ1A = 0,15;
b.) Läuferstrom I2A = 200 A.
Die Sättigung und alle Verluste außer den Kupferverlusten im Läufer können vernachlässigt wer-
den.
1. Wie groß sind der Strom, das Moment und der Schlupf des Motors im Kipppunkt?
2. Wie groß ist die mechanische Leistung und der Schlupf bei maximalem cos(ϕ)?
3. Wie groß ist der Läuferwiderstand R2 (den man an der Rotorklemmen messen kann)?
Zusatzfrage: Welche Läuferspannung ergibt sich im Stillstand bei offenen Schleifringen, wenn der
Ständer an Nennspannung liegt?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

103. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 103 von 108
Aufgabe AsyM 2 (Ortskurve, Kippstrom, -schlupf, Wirkungsgrad, Drehmoment)
Eine Asynchronmaschine hat die Daten
Mn = 31,8 Nm; nn = 2800 1/min;
fn = 50 Hz; p = 1;
cosϕn = 0,8; Un = 400 V;
I0 = 6 A;
Die Ständerverluste, die mechanischen Verluste und die Sättigung sind zu vernachlässigen.
1. Berechnen Sie den Nennstrom In, den Nennschlupf sn und den Nennwirkungsgrad ηn.
2. Zeichnen Sie die Ortskurve des Ständerstromes und bestimmen Sie den Anfahrstrom IA.
3. Wie groß sind das maximale Drehmoment MKipp und der Wirkungsgrad ηKipp im Kipppunkt?
Aufgabe AsyM 3 (Käfigläufer, Induktion, Verlustleistung, idealer und realer Heyland-Kreis)
Ein Drehstromasynchronmotor mit Käfigläufer hat die Nenndaten:
fn= 50 Hz; Pn = 45 kW; nn =732 1/min; Un = 400 V; In = 89 A; MKipp/Mn = 2,2.
Außer den Stromwärmeverlusten im Läufer sollen hier keine Verluste berücksichtigt werden.
1. Wie groß ist die Leerlaufdrehzahl der Maschine?
2. Welche Frequenz hat die im Läufer induzierte Spannung im Nennpunkt?
3. Wie groß ist bei Nennbetrieb die als Wärme aus dem Läufer abzuführende Verlustleistung?
4. Wie groß ist im Nennpunkt cos ϕn ?
5. Zeichnen Sie den Heyland-Kreis (Stromortskurve) mit dem Maßstab 20 A/cm; Stromverdrän-
gung soll dabei zunächst nicht berücksichtigt werden.
6. Welcher Leerlaufstrom ergibt sich aus dem Heyland-Kreis?
7. Tatsächlich hat die Maschine durch Stromverdrängung ein Anzugsmoment von MA/Mn = 2,2
und einen Anlaufstrom von IA = 490 A. Tragen Sie den tatsächlichen Anlaufpunkt in den Hey-
landkreis ein. Ergänzen Sie dann den ungefähren Verlauf der Stromortskurve der realen Ma-
schine im Bereich Leerlaufpunkt bis Anlaufpunkt.
Zusatzfrage: Die Maschine soll nun mit einer etwas niedrigeren Spannung von 380 V betrieben
werden. Wie groß sind dafür Leerlaufstrom und Kippmoment?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

104. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 104 von 108
Aufgabe AsyM 4 (Kurzschlussläufer, Auslegung d. Polpaarzahl, Ortskurve)
Ein im Stern geschalteter Asynchronmotor (Kurzschlussläufer) für ein 400 V / 50 Hz Drehstrom-
netz soll näherungsweise auf zwei Betriebspunkte ausgelegt werden.
a) M = 318,3 Nm bei 700 min-1 (Nennpunkt)
b) M = 636,6 Nm bei 0 min-1
Die Ständerverluste sind zu vernachlässigen. Der Leerlaufstrom beträgt I0 = 40 A.
1. Bestimmen Sie die günstigste Polpaarzahl im Hinblick auf die Betriebsanforderungen und den
Wirkungsgrad.
2. Welche Leistung nimmt die Maschine in den beiden Betriebspunkten auf, wie groß sind die
Verlustleistungen im Rotor?
3. Zeichnen Sie das auf die Ständerseite bezogene Ersatzschaltbild und berechnen Sie dessen E-
lemente.
4. Zeichnen Sie die Ortskurve des Ständerstromes.
a) Wie groß ist die Blindleistung für den Betriebsfall b)?
b) Welche maximale Wirkleistung lässt sich mit der Maschine in ein starres Netz zurück-
speisen?
Aufgabe AsyM 5 (Kreisdiagramm des Stromes, Überlastpunkt, Umkehrung der Drehrichtung)
Für eine Asynchronmaschine sind folgende Werte gegeben:
Un = 400 V; In = 60 A; cos ϕn = 0,82; p = 2; f = 50 Hz.
Bei einer Kurzschlussmessung mit reduzierter Spannung werden darüber hinaus folgende Werte
ermittelt: U = 100 V; I = 36 A; cos ϕ = 0,34.
Außer den Kupferverlusten im Läufer können alle Verluste vernachlässigt werden.
1. Konstruieren Sie das Kreisdiagramm des Stromes (1 cm = 10 A) und ermitteln Sie für den
ˆ
Nennbetrieb
a) den Leerlaufstrom I0,
b) die Nenndrehzahl nn,
c) den Wirkungsgrad ηn und
d) das Nennmoment Mn.
2. Die Maschine wird mit dem 1,3-fachen Nennmoment belastet. Ermitteln sie für den sich ein-
stellenden stabilen Betriebspunkt
a) den Ständerstrom,
b) die Drehzahl und
c) den Leistungsfaktor.
Zusatzfrage: Aus dem Leerlauf (synchrone Drehzahl) heraus soll durch Vertauschen von 2 Phasen
die Drehrichtung der Maschine umgekehrt werden (Reversieren).
Wie groß ist der Schlupf direkt nach dem Umschalten?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

105. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 105 von 108
Aufgabe AsyM 6 (6-poliger AsyM, Stromortskurve)
Von einem sechspoligen Asynchronmotor sind aus dem Berechnungsgang die folgenden Daten
bekannt:
Un = 440 V (Y), fn = 60 Hz, X0 = 7,26 Ω, X2σ` = 0,41 Ω, R2` = 67 mΩ
1. Welchen Leerlaufstrom wird die Maschine aufnehmen?
2. Bestimmen Sie den ideellen Kurzschlusspunkt P∞ und zeichnen Sie die Stromortskurve (Maß-
stab: 40 A/cm).
3. Bestimmen Sie den Anlaufpunkt PA in der Stromortskurve. Wie groß sind Leistungsmaßstab,
Drehmomentmaßstab, Anlaufdrehmoment und Anlaufstrom?
4. Bestimmen Sie Kippmoment und Kippschlupf.
5. Legen Sie den Nennpunkt der Maschine so fest, dass die Maschine in diesem Punkt mit maxi-
malem Leistungsfaktor arbeitet. Wie groß sind Nennstrom, -schlupf, -drehzahl und -
drehmoment?
6. Wie groß sind im Nennbetrieb Leistungsfaktor sowie aus dem Netz aufgenommene Wirk-,
Blind- und Scheinleistung?
Aufgabe AsyM 7 (Heyland-Kreis, Bestimmung der Bauteile des ESB)
Gegeben ist ein Drehstromasynchronmotor mit Schleifringläufer mit folgenden Nenndaten:
Un = 400V
fn = 50 Hz
In = 75 A
p =2 (Anzahl Polpaare)
Das größte Anlaufmoment ergibt sich, wenn der externe Läufervorwiderstand auf den 5-fachen
Wert des Widerstandes der Läuferwicklung eingestellt wird. Dafür wird gemessen:
I1A = 150 A (Anlaufstrom)
P1A = 64,5 kW (aufgenommene Leistung)
Verwenden Sie das übliche einphasige Ersatzschaltbild (Sternschaltung) mit den üblichen Verein-
fachungen.
1. Wie groß sind die Leerlaufdrehzahl des Motors und die Scheinleistung im Nennpunkt?
2. Zeichnen Sie den Heylandkreis (motorischer Bereich) für die Maschine; (entweder normiert
mit 1 = 50 mm oder mit dem Maßstab 1 A = 1 mm). Geben Sie den Gang der Konstruktion
stichwortartig an. (Hinweis: Interpretieren Sie zur Konstruktion des Kreises die oben getroffe-
ne Aussage "... das größte Anlaufmoment...".)
3. Zeichen Sie das einphasige Ersatzschaltbild und ermitteln Sie die Größen der vorkommenden
Reaktanzen X und der Widerstände. Geben Sie die Größe des Vorwiderstandes an. (wie R2'
auf den Ständer bezogen)
4. Wie groß sind Anlaufstrom, Anlaufmoment, Kippmoment und Kippschlupf bei kurzgeschlos-
senen Schleifringen? Verwenden Sie möglichst den Heylandkreis.
5. Es wird vorgeschlagen, zur Begrenzung des Anlaufstromes drei Drosselspulen (XL' = 0,8 Ω
bei 50 Hz) statt der Widerstände in den Läuferkreis zu schalten. Ergänzen Sie das Diagramm
aus 2.2 um den veränderten Heylandkreis und geben Sie das Kippmoment für diesen Betriebs-
zustand an.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

106. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 106 von 108
Aufgabe AsyM 8 (Generatorbetrieb)
Die Nennspannung und die Nennfrequenz sind mit Un = 400 V und fn = 50 Hz fest vorgegeben.
Aus Messungen an der Asynchronmaschine wird die Leerlaufinduktivität zu 0,147 H bestimmt.
Der Anfahrstatorstrom im Motorbetrieb beträgt 65 A und die Polpaarzahl p = 2.
Zunächst wird die Maschine als Generator betrieben und liefert im Nennpunkt eine elektrische
Leistung von P = 10,25 kW bei einem Leistungsfaktor von 0,87 in das Netz.
1. Berechnen Sie den Leerlaufstrom sowie den Statorstrom im Generatornennpunkt.
2. Konstruieren Sie den Heylandkreis der Maschine (Achsen beschriften!). Markieren Sie den
Nennpunkt für den Generatorbetrieb und tragen sie die Leistungsgerade ein. (Maßstab 5 A/cm)
3. Bestimmen Sie den Schlupf und das Moment für den Generatorbetrieb im Nennpunkt.
4. Tragen Sie den Kipppunkt für den Motorbetrieb in Ihren Heylandkreis ein und bestimmen Sie
das Moment in diesem Punkt.
Die Asynchronmaschine soll als „Bremse“ (s > 1) arbeiten und ein Gegenmoment von 59 Nm
erzeugen.
6. Markieren Sie den Bremspunkt in ihrem Heylandkreis und bestimmen Sie den Schlupf in die-
sem Punkt.
6.4 Synchronmaschine
Aufgabe SyM 1 (Ersatzschaltbild, Nenngrößen, Kurzschluss)
Ein Drehstrom-Synchrongenerator hat folgende Daten:
Un = 450 V; cos ϕn= 0,8 (übererregt); Sn = 670 kVA;
fn= 60 Hz; nn = 720 1/min;
bezogene synchrone Reaktanz xd = 250 %
Verluste in der Maschine und Sättigungseinflüsse sind für diese Aufgabe zu vernachlässigen.
1. Zeichnen Sie das einphasige Ersatzschaltbild für den Generator (für stationäre Zustände) und
tragen Sie Zählpfeile für die Ströme und Spannungen ein.
2. Ermitteln Sie die folgenden Größen für die Maschine:
a) Anzahl der Polpaare p der Maschine,
b) Nennstrom In,
c) synchrone Reaktanz Xd in Ω,
d) Nenndrehmoment Mn und
e) Dauerkurzschlussstrom Ik0 bei Leerlauferregung.
3. Zeichnen Sie die (zu dem ESB passende) Ortskurve des Statorstromes für Nennspannung und
Nennerregung. Markieren Sie den Nennpunkt (Maßstab: 150 A/cm).
4. Um welchen Winkel läuft der Rotor dem mit der Statorwicklung verketteten magnetischen
Fluss voraus oder hinterher?
5. Der Generator soll bei einem Kurzschluss den 3-fachen Nennstrom als Dauerkurzschlussstrom
erzeugen können. Wie groß muss in diesem Fall der Erregerstrom bezogen auf den Nenner-
regerstrom eingestellt sein?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

107. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 107 von 108
Aufgabe SyM 2 (Energieversorgung einer Offshore-Plattform, Zeigerbild)
Für die Energieversorgung einer Offshore-Plattform wird ein Synchrongenerator mit bürstenloser
Erregung eingesetzt, der von einer Gasturbine angetrieben wird. Die Daten des Generators lauten:
Un = 6 kV, Sn = 7600 kVA, cos ϕn = 0,8 (übererregt), nn = 1500 min-1, ηn = 0,94, fn = 50 Hz
Die bezogene synchrone Reaktanz der Maschine beträgt xd = 1,3. Im Nennbetrieb beträgt der Er-
regerstrom In = 20 A. Der Ständerwiderstand und Sättigungserscheinungen sollen vernachlässigt
werden (Up ∼ Ie).
1. Berechnen Sie Polpaarzahl, Nennstrom.
2. Wie groß ist das Leerlauf-Kurzschluss-Verhältnis und die synchrone Reaktanz in Ohm?
3. Zeichnen Sie die Stromortskurven (Parameter: Polradwinkel ϑ) der Maschine für Nenner-
regerstrom und halben Nennerregerstrom.
4. Ergänzen Sie in dem Diagramm das Zeigerdiagramm für Nennbetrieb (Ströme und Spannun-
gen).
5. Wie groß ist der Nennlastwinkel und das Kippmoment bei Nennerregung?
6. Wie groß ist der Leerlauferregerstrom?
Zusatzfrage 1: Mit welcher mechanischen Leistung wird der Generator im Nennbetrieb angetrie-
ben und wie groß ist das Nenndrehmoment?
Zusatzfrage2: Auf welchen Wert muss der Erregerstrom eingestellt werden, um bei Nennwirkleis-
tung den Leistungsfaktor cos ϕ = 1 zu erreichen? Welcher Ständerstrom fließt in diesem Betriebs-
zustand?
Aufgabe SyM 3 (Ersatzschaltbild, Zeigerbild)
Eine einpolpaarige Dreiphasen-Synchronmaschine speist ein Netz Un = 10 kV, fn = 50 Hz. Die
Verluste der Ständerwicklung werden nicht berücksichtigt. Die synchrone Reaktanz beträgt Xd = 1
Ω.
1. Zeichnen Sie das einphasige Ersatzschaltbild der Maschine. Geben Sie die zugehörige Span-
nungs-Gleichung an.
2. Die Synchronmaschine soll im Generatorbetrieb eine Wirkleistung von P = 34,6 MW abgeben.
Hierbei soll sie in drei verschiedenen Fällen
a) Blindleistung von Q = 17,3 MVA wird abgeben (übererregt);
b) keinerlei Blindleistung wird aufgenommen oder abgegeben;
c) Blindleistung von Q = 25,9 MVA wird (untererregt).
Zeichnen Sie die Zeigerdiagramme für die 3 verschiedenen Betriebszustände und ermitteln Sie die
Polradspannung Up und den Polradwinkel ϑ.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg

108. Vorlesung: „Elektrische Maschinen“ 10/11 Seite 108 von 108
Aufgabe SyM 4 (Zeigerbild)
Ein Synchronmotor (s. Ersatzschaltbild) werde an einem starren Netz betrieben. Sättigungseffekte
und ohmsche Verluste sollen vernachlässigt werden.
I1 Xd
U1 Up
1. Für einen bestimmten Betriebszustand beträgt die Netzspannung U1 = (240 - j0) V und die Ma-
schine nimmt einen Strom von I = (50 - j62,5) A auf. Dabei nimmt die Maschine ihre Nenn-
wirkleistung auf. Der Polradwinkel wird zu 32° bestimmt. Der Erregerstrom in diesem Fall ist
Ie = 15 A.
Zeichnen Sie das Zeigerdiagramm der Maschine (Maßstäbe: 1 cm = 20 V und 1 cm = 20 A).
ˆ ˆ
Ermitteln Sie daraus folgende Größen
a) Betrag der Polradspannung Up des Ersatzschaltbildes
b) die synchrone Reaktanz Xd des Ersatzschaltbildes
c) cos ϕ
d) die aufgenommene Scheinleistung
e) Nennwirkleistung
f) Ist die Maschine unter- oder übererregt?
2. Im Nennpunkt ist der cos ϕ = 0,71 (übererregt). Die Nennspannung ist gleich der oben in 1.
angegebenen Spannung. Ermitteln Sie im Zeigerdiagramm für den Nennpunkt:
a) Betrag und Phasenlage des Stromes I1
b) Scheinleistung
c) Betrag der Polradspannung
d) Erregerstrom
Zusatzaufgabe: Tragen Sie jeweils die Ortskurven ein!
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg