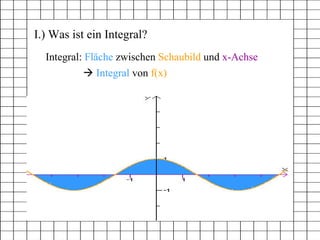
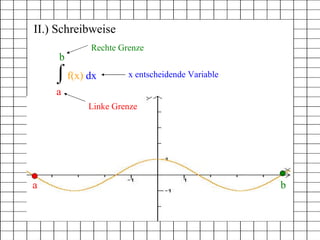
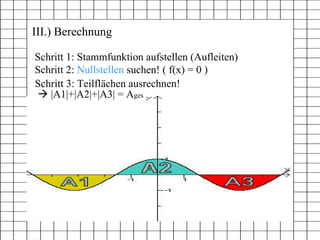
Das Dokument behandelt das Thema Integralrechnung und beschreibt die Definition, Schreibweise, Berechnungsmethoden sowie ein praktisches Beispiel. Es erläutert die Schritte zur Aufstellung der Stammfunktion sowie die Berechnung des Integrals zwischen zwei Grenzen anhand eines Beispiels und der Nutzung eines Computer-Algebra-Systems (CAS). Zusätzlich wird eine weiterführende Aufgabe zur Berechnung der Fläche zwischen zwei Funktionen vorgestellt.

1. Integrale Roman Steddin und Michael Tilli

2. Gliederung: ) Was ist ein Integral? II. ) Schreibweise III.) Berechnung IV.) Beispiel V. ) Berechnung CAS VI.) Weiterführende Aufgabe

3. I.) Was ist ein Integral? Integral: Fläche zwischen Schaubild und x-Achse  Integral von f(x)

4. II.) Schreibweise b a f(x) dx Rechte Grenze Linke Grenze x entscheidende Variable a b

5. III.) Berechnung Schritt 1: Stammfunktion aufstellen (Aufleiten) Schritt 2: Nullstellen suchen! ( f(x) = 0 ) N1 N2 N3 N4  |A1|+|A2|+|A3| = A ges Schritt 3: Teilflächen ausrechnen!

6. IV.)Beispiel:  f(x) = 5x^3 + 3x^2 + 4x^1 f(x)= 5x^2 + 3x + 4 Schritt 1: Stammfunktion aufstellen  Aufleiten = Ableiten rückwärts  f(x)= 5x^2 +3x^1 + 4*(x^0 ) (+1) (+1) (+1) 1.) Exponenten um 1 erhöhen (+1)  F(x) = 5/ 3 x^3+3/ 2 x^2+4/ 1 x 2.) Neue Exponenten als Quotienten unter Faktor schreiben  f(x) = 5x^ 3 + 3x^ 2 + 4x^ 1

7. ... [F(x)] a b  F( b ) – F( a ) = Integral Rechte Grenze (=4) Linke Grenze (= -1) Schritt 2:  5/3*4^3+3/2*4^2+4/1*4 - (5/3 -1^3+3/2 -1^2 + 4/1 -1) F(b) – F(a) = Integral = 905/6

8. V.)Berechnung mit CAS: (f(x), x, Linke Grenze, Rechte Grenze) Beispiel: f(x) = 5x^2 + 3x + 4 ( f(x), x, Linke Grenze , Rechte Grenze ) ( f(x), x, -1 , 4 ) = 905/6 keine Nullstellen ( f(x) =0) vorhanden

9. VI.)Weiterführende Aufgabe: Fläche zwischen zwei Schaubildern (f(x) u. g(x) Schritt 1: Integral von f(x) ausrechnen Schritt 2: Integral von g(x) „ausstanzen“  f(x) – g(x)