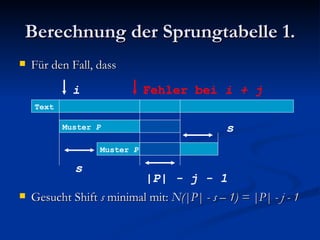
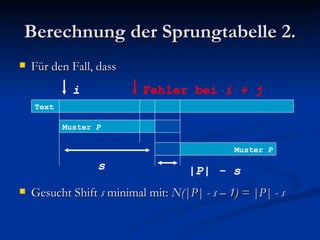
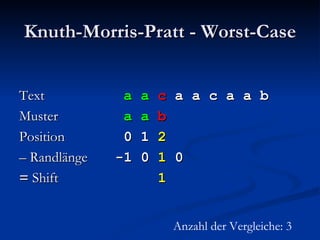
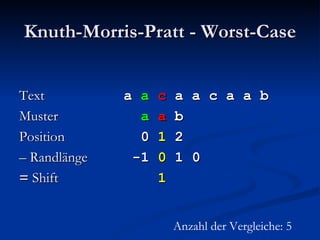
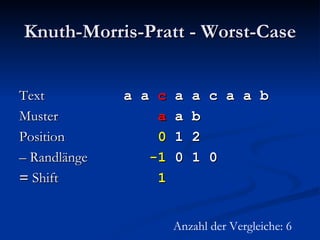
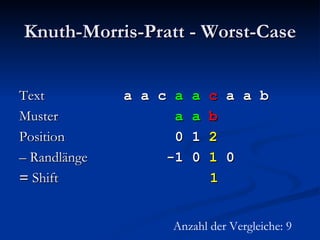
Der Boyer-Moore-Algorithmus ist ein effizienter Textsuchalgorithmus, der beim Suchen nach kurzen Mustern in langen Texten mithilfe von Techniken wie der 'Bad Character'- und 'Good Suffix'-Regel arbeitet. Er übertrifft andere Algorithmen wie die naive Suche und den Knuth-Morris-Pratt-Algorithmus, insbesondere bei größeren Alphabeten und weniger Wiederholungen im Muster. Der Algorithmus hat eine durchschnittliche Laufzeit, die sich bei großen Texten auf bis zu 3(n + m) verringern kann, was ihn für die praktische Anwendung vorteilhaft macht.

1. Boyer-Moore-Algorithmus Ein Textsuchalgorithmus für große Alphabete Martin Szugat (Martin.Szugat@GMX.net)

2. Agenda Evolution: Von der naiven Suche über Knuth-Morris-Pratt zu Boyer-Moore Schlechte Zeichen und gute Suffixe Boyer-Moore vom Anfang bis zum Ende Fazit: Der Durchschnitt siegt!

3. Problemstellung Exakte Suche von kurzen Zeichenfolgen in langen Zeichenfolgen

4. Zur Erinnerung!!! Das Muster (engl. Pattern) ist die gesuchte Zeichenfolge. Der Text ist die durchsuchte Zeichenfolge. Als ( Mis- ) Match wird die (Nicht-)Überein-stimmung von einem Zeichen aus dem Muster mit einem Zeichen im Text bezeichnet. Nach einem Mismatch wird das Muster im Text verschoben, was als Shift bezeichnet wird.

5. Lösung I: Naive Suche Vergleiche die Zeichen des Musters mit den Zeichen des Textes, solange wie kein Mismatch auftritt. Bei einem Mismatch verschiebe das Muster um ein Zeichen im Text und beginne von vorne. Falls alle Zeichen übereinstimmen, wurde ein Treffer erzielt.

6. Naive Suche - Beispiel Text aaaabaaaac... Muster aaaac Anzahl der Vergleiche: 0

7. Naive Suche - Beispiel Text a aaabaaaac... Muster a aaac Anzahl der Vergleiche: 1

8. Naive Suche - Beispiel Text a a aabaaaac... Muster a a aac Anzahl der Vergleiche: 2

9. Naive Suche - Beispiel Text aaaa b aaaac... Muster aaaa c Anzahl der Vergleiche: 5

10. Naive Suche - Beispiel Text aaaa b aaaac... Muster aaaa c Anzahl der Vergleiche: 5

11. Naive Suche - Beispiel Text a aaa b aaaac... Muster aaa a c Anzahl der Vergleiche: 9

12. Naive Suche - Beispiel Text aa aa b aaaac... Muster aa a ac Anzahl der Vergleiche: 12

13. Naive Suche - Beispiel Text aaaab aaaac ... Muster aaaac Anzahl der Vergleiche: 20

14. Naive Suche - Laufzeit Um in einem Text der Länge n ein Muster der Länge m zu finden, benötigt die naive Suche maximal m (n – m + 1) Vergleiche.

15. Lösung II: Knuth-Morris-Pratt Idee: Größere Shifts durch Wiederholungen von Zeichenfolgen im Muster. Algorithmus: Berechne die Länge der eigentlichen Ränder aller Präfixe des Musters. Vergleiche das Muster mit dem Text. Bei einem Mismatch verwende die Ränderlängen, um das Muster im Text zu verschieben.

16. Länge der Ränder aller Präfixe Muster ε a b a b c Randlänge Leeres Wort

17. Länge der Ränder aller Präfixe Muster ε a b a b c Randlänge -1 Per Definition Leeres Wort

18. Länge der eigentlichen Ränder aller Präfixe Muster ε a b a b c Randlänge -1 0 0

19. Länge der Ränder aller Präfixe Muster ε a b a b c Randlänge -1 0 0 1

20. Länge der Ränder aller Präfixe Muster ε a b a b c Randlänge -1 0 0 1 2

21. Länge der Ränder aller Präfixe Muster ε a b a b c Randlänge -1 0 0 1 2 0

22. Knuth-Morris-Pratt - Beispiel Text a b a b a b c ... Muster a b a b c

23. Knuth-Morris-Pratt - Beispiel Text a b a b a b c ... Muster a b a b c Position 0 1 2 3 4 - Randlänge -1 0 0 1 2 0 = Shift 2 Anzahl der Vergleiche: 5

24. Knuth-Morris-Pratt - Beispiel Text a b a b a b c ... Muster a b a b c Anzahl der Vergleiche: 5

25. Knuth-Morris-Pratt - Beispiel Text a b a b a b c ... Muster a b a b c Anzahl der Vergleiche: 6

26. Knuth-Morris-Pratt - Beispiel Text a b a b a b c ... Muster a b a b c Anzahl der Vergleiche: 8

27. Knuth-Morris-Pratt - Laufzeit Für die eigentliche Suche: 2n – m + 1 Für die Tabelle mit den Längen der Ränder: 2m - 1 Für den KMP-Algorithmus insgesamt: 2n + m

28. Knuth-Morris-Pratt - Worst-Case Text a a c a a c a a b Muster a a b Position 0 1 2 – Randlänge -1 0 1 0 = Shift 1 Anzahl der Vergleiche: 3

29. Knuth-Morris-Pratt - Worst-Case Text a a c a a c a a b Muster a a b Position 0 1 2 – Randlänge -1 0 1 0 = Shift 1 Anzahl der Vergleiche: 5

30. Knuth-Morris-Pratt - Worst-Case Text a a c a a c a a b Muster a a b Position 0 1 2 – Randlänge -1 0 1 0 = Shift 1 Anzahl der Vergleiche: 6

31. Knuth-Morris-Pratt - Worst-Case Text a a c a a c a a b Muster a a b Position 0 1 2 – Randlänge -1 0 1 0 = Shift 1 Anzahl der Vergleiche: 9

32. Knuth-Morris-Pratt - Worst-Case Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 14

33. Bad Character Definition: Ein Zeichen, welches einen Mismatch auslöst, wird Bad Character genannt. Problem: Das Bad Character wird beim Shift nicht berücksichtigt Folge: Das Muster wird im schlechtesten Fall stets nur um ein Zeichen verschoben. Sonderfall: Das Bad Character taucht im Muster überhaupt nicht auf. Lösung: Falls das Bad Character nicht im Muster vorkommt, verschiebe das Muster um die volle Länge.

34. Bad Character – Beispiel I Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 3

35. Bad Character - Beispiel I Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 6

36. Bad Character - Beispiel I Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 9

37. Muster von rechts nach links vergleichen Problem: Es müssen weiterhin alle Zeichen im Text mindestens einmal mit einem Zeichen aus dem Muster verglichen werden. Lösung: Vergleiche das Muster von rechts nach links mit dem Text. Vorteil: Bad Character werden schneller erkannt!

38. Bad Character - Beispiel II Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 1

39. Bad Character - Beispiel II Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 2

40. Bad Character - Beispiel II Text a a c a a c a a b Muster a a b Anzahl der Vergleiche: 5

41. Bad Character-Regel Sei A das verwendete Alphabet, und c ein Zeichen aus dem Alphabet A , dann liefert die Funktion s(c) die Position des letzten Auftretens von c im Muster den Wert -1 , falls c nicht im Muster auftaucht. Für einen Mismatch an Position j gilt: Shift = j – s(c) , sofern s(c) < j

42. Bad Character-Regel - Laufzeit Im Best-Case hat der Boyer-Moore-Algorithmus dank der Bad Character-Regel eine Laufzeit von n / m Im Worst-Case hat er mit der Bad Character-Regel alleine jedoch eine Laufzeit von n · m

43. Sprungtabelle Der Boyer-Moore-Algorithmus benötigt zusätzlich eine Sprungtabelle, um auch im Worst-Case eine Laufzeit linear zu n zu erreichen. Vorgehen: Berechne die Längen der Teilzeichenfolgen des Musters, die auch Suffixe des Musters sind.  Good Suffix Berechne die Sprungtabelle.

44. Good Suffix - Beispiel Text: Wiederholung von baabaabaaaabaabaabaaaabaabaabaaaa... baabaabaaba Muster Anzahl der Vergleiche: 0

45. Good Suffix - Beispiel Text: Wiederholung von baabaabaa a a baabaabaaaabaabaabaaaa... baabaabaa b a Muster Anzahl der Vergleiche: 2

46. Good Suffix - Beispiel Text: Wiederholung von baabaaba a aaba abaabaaaabaabaabaaaa... baabaa b aaba Muster Anzahl der Vergleiche: 7 Shift um 2

47. Good Suffix - Beispiel baabaaba a aaba abaabaaaabaabaabaaaa... baabaa b aaba Anzahl der Vergleiche: 7 Weak Good Suffix!

48. Good Suffix - Beispiel baabaaba a aabaaba abaaaabaabaabaaaa... baa b aabaaba Anzahl der Vergleiche: 15 Mismatch an derselben Stelle im Text mit dem gleichen Zeichen im Muster! Shift um 3

49. Strong Good Suffix-Regel Problem: Mit einer Weak Good Suffix-Regel hat der Boyer-Moore-Algorithmus in diesem Fall eine Laufzeit von (n · m) / 6 Lösung: Strong Good Suffix-Regel Vorteil: An der Stelle, an der ein Mismatch erfolgte, befindet sich nach einem Shift ein anderes Zeichen als jenes, welches den Mismatch verursachte.

50. Strong Good Suffix - Beispiel Text: Wiederholung von baabaabaa a a baabaabaaaabaabaabaaaa... aaabaabaa b a Muster Anzahl der Vergleiche: 2

51. Strong Good Suffix - Beispiel Text: Wiederholung von baabaaba a aaba abaabaaaabaabaabaaaa... aaabaa b aaba Muster Anzahl der Vergleiche: 7 Shift um 2

52. Strong Good Suffix - Beispiel baabaaba a aaba abaabaaaabaabaabaaaa... aaabaa b aaba Anzahl der Vergleiche: 7 Weak Good Suffix

53. Strong Good Suffix - Beispiel baabaaba a aaba abaabaaaabaabaabaaaa... aaabaa b aaba Anzahl der Vergleiche: 7 Strong Good Suffix!

54. Strong Good Suffix - Beispiel baabaaba a aaba abaaba aaabaabaabaaaa... a aaba abaaba Anzahl der Vergleiche: 18 Shift um 6 Bereits überprüfter Bereich wird erneut verglichen.

55. Kein Strong Good Suffix?! baabaaba a aaba abaabaaaabaabaabaaaa... baabaa b aaba Anzahl der Vergleiche: 7 Weak Good Suffix

56. Regel für die Ränder Problem: Die übereinstimmende Zeichenfolge kommt kein zweites Mal (als Strong Good Suffix ) im Muster vor. Folge: Die Sprungtabelle liefert für diesen Fall einen Shift von 0! Lösung: Eine 2. Sprungtabelle wird berechnet, welche die eigentlichen Ränder des Musters berücksichtigt.

57. Randregel - Beispiel baabaaba a aaba abaabaaaabaabaabaaaa... baabaa b aaba Anzahl der Vergleiche: 7 In einer 2. Sprungtabelle werden die eigentlichen Ränder des Musters berücksichtigt.

58. Randregel - Beispiel baabaabaaaa ba abaabaa a a baabaabaaaa... ba abaabaa b a To be continued ... Anzahl der Vergleiche: 9 Vorheriger Mismatch

59. Boyer-Moore: Top-Down Berechne die Tabelle für die Bad Character-Regel und die Sprungtabelle (Strong Good Suffix und Randregel). Vergleiche das Muster mit dem Text, solange bis ein Mismatch auftritt. Bei einem Mismatch ermittle anhand der aktuellen Position den Sprungwert für die Bad Character-Regel und für die Sprungtabelle. Führe den größeren der beiden Shifts durch.

60. Algorithmus für die Bad Character-Regel Erzeuge eine Tabelle mit der Größe des verwendeten Alphabets und initialisiere die Felder mit dem Wert -1 . Durchlaufe das Muster von links nach rechts und speichere die Position des aktuellen Zeichens in der Tabelle. Als Index verwende das Zeichen. Beispiel „abcab“: &quot;a&quot;  3, &quot;b&quot;  4, &quot;c&quot;  2, &quot;d&quot;  -1, ...

61. Algorithmus für die Sprungtabelle Berechne eine Zwischentabelle mit den Längen der Teilzeichenfolgen, die ein starkes Suffix des Musters sind. Berechne anhand der Zwischentabelle die Sprungtabelle 1. für die Strong Good Suffix-Regel und die Sprungtabelle 2. für die Randregel. Kombiniere beide Sprungtabellen.

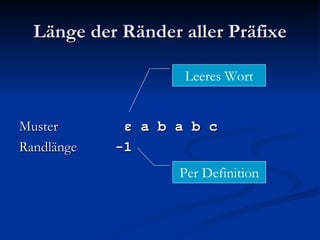
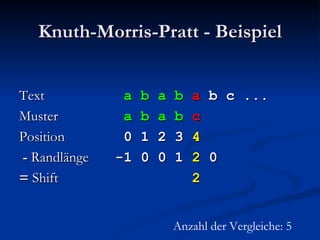
62. Berechnung der Zwischentabelle Index i 0 1 2 3 4 5 6 7 8 Muster P b a b a c b a b a Suffixlänge N(i) 0 2 0 4 0 0 2 0 - N(i):= max{j: j ≥ 0 Λ P[(i – j + 1)..i] ist Suffix von P}

63. Berechnung der Zwischentabelle Index i 6 Muster P b a b a c b a b a Suffixlänge N(i) 2 N( 6 ):= max{j: j ≥ 0 Λ P[( 6 – j + 1).. 6 ] ist Suffix von P} = 2

64. Algorithmus für die Berechnung der Zwischentabelle (1) Durchsuche das Muster von rechts nach links per Brute-Force nach einem Suffix des Musters. d c b a b a c b a i,e b a a N(i) = i – a Muster P

65. Algorithmus für die Berechnung der Zwischentabelle (2) Falls gilt: a < i < e Wird N(i) mit N(|P| + i - e - 1) berechnet. 1. Fall: N(|P| + i - e - 1) < i - a d c b a b a c b a b a i c b a b a N(i) = N(|P| + i – e - 1) N(3) = N(8) = 2 e a c b a b a

66. Algorithmus für die Berechnung der Zwischentabelle (3) 2. Fall: N(|P| + i - e - 1) >= i - a a b a b a c b a b a i b a b a N(i) >= N(|P| + i – e - 1) N(2) = N(7) + 1 = 2 + 1 = 3 e a b a b a

67. Berechnung der Sprungtabelle 1. Für den Fall, dass Gesucht Shift s minimal mit: N(|P| - s – 1) = |P| - j - 1 Text Muster P Muster P Fehler bei i + j i s |P| - j - 1 s

68. Berechnung der Sprungtabelle 2. Für den Fall, dass Gesucht Shift s minimal mit: N(|P| - s – 1) = |P| - s Text Muster P Muster P Fehler bei i + j i s |P| - s

69. Laufzeiten bei Boyer-Moore I Für die Berechnung der Bad Character-Regel: Abhängig von der Größe des Alphabets Allerdings: Keine Zeichenfolgenvergleiche Sondern: Nur Speicherzugriffe über einen Index Für die Berechnung der Sprungtabelle 1. und 2.: Vergleichbar zum KMP Laufzeit: linear

70. Laufzeiten bei Boyer-Moore II Für die eigentliche Suche: Unterscheidung zwischen initialen und wiederholten Vergleichen mit einem Zeichen im Muster Laufzeit: linear Für den Boyer-Moore-Algorithmus insgesamt: Aufwendige Analyse Maximal 3(n + m) Vergleiche notwendig

71. Fazit: Vorteile von Boyer-Moore Bad Character-Regel  Große Alphabete: Proteine Muster von rechts nach links vergleichen  Im Best-Case eine Laufzeit von n / m Strong Good Suffix-Regel  Im Worst-Case eine Laufzeit von 3 (n + m)

72. Vergleich zu Knuth-Morris-Pratt Um so größer das verwendete Alphabet ist und um so weniger Wiederholungen das Muster und der Text enthält, um so stärker nähert sich die tatsächliche Laufzeit der Laufzeit im Best-Case an. 3 (n + m) 2 (n + m) Worst-Case n / m 2 (n + m) Best-Case Boyer-Moore Knuth-Morris-Pratt Algo Case

73. Noch Fragen??? May the source be with you ...