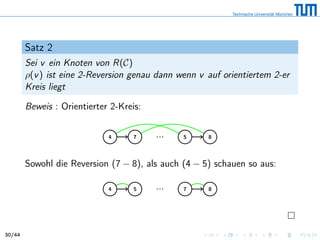
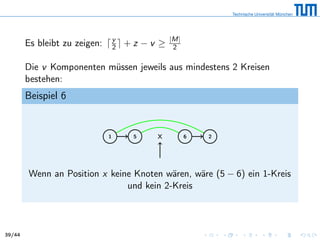
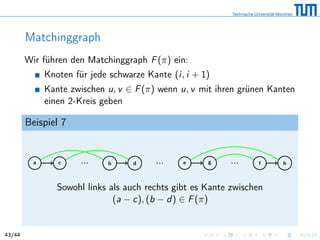
Das Dokument behandelt das Problem der minimalen Sortierung von Permutationen durch Umkehrungen (Reversals), ein Konzept, das in der Biologie relevant ist, um evolutionäre Abstände zu bestimmen. Es wird eine 3/2-Approximation vorgestellt, die auf der Analyse von Breakpoints und zirkulären Graphen basiert, um die Anzahl der erforderlichen Reversals zu minimieren und einen effizienten Algorithmus zu entwerfen. Zudem werden verschiedene mathematische Lemmas und Sätze bewiesen, die die Beziehung zwischen diesen Graphen und der Anzahl der notwendigen Reversals zur Sortierung reflektieren.

1. Eine 3
2-Approximation für
Sorting by Reversals
Andreas Stephan
July 16, 2014
1/44

2. Was ist eine Reversion?
Sei π unsere zu sortierende Permutation
Eine Reversion ist ein "Umdrehen einer Teilfolge"
Beispiel 1
π = 13 5892
ρ3,6(π)
467 → π = 13 2985 467
2/44

3. Motivation
Problematik kommt aus der Biologie
Veränderungen der DNA oft durch "Reversionen"
Wenn man Anzahl an Reversionen findet, bekommt man eine
Idee für den sogenannten evolutionären Abstand
3/44

4. Problemstellung
Das Problem heißt Min-SBR(Minimum - Sorting by Reversals)
Eingabe: Permutation π
Gesucht: Eine kürzeste Folge an Reversionen (p1, p2, · · · , pd ),
sodass ρd (ρd−1(. . . ρ1(π)) . . . ) = (1 . . . n)
4/44

5. Breakpoints
Breakpoint: Tupel an Positionen (i, i + 1), die nicht nebeneinander
gehören(Im Beispiel durch "|" dargestellt)
Beispiel 2
1|345|8|9|2|67
Anzahl Reversionen in Abhängigkeit zu Breakpoints
Ziel wird sein diese zu eliminieren
b(π) ist Anzahl an Breakpoints
5/44

6. Kreisgraphen
Bezeichnet als G(π).
Für ihn wird die erweiterte Permutation π gebildet mit
π := (0, π(1), . . . .π(n), n + 1)
Knoten: V := {0, . . . , n + 1}
Kantenmenge: Schwarze und grüne Kanten.
Kante (i, j) schwarz, wenn sie nebeneinander liegen(gerichtet)
Kante {i, j} grün, wenn sie nebeneinander liegen
wollen(ungerichtet)
6/44

7. Beispiel
0 7 5 6 3 2 4 1 8
Figure : Kreisgraph von [7563241]
7/44

8. Kreisdekompositionen
Kreis soll abwechselnd grüne und schwarze Kanten haben
Länge k eines Kreises ist Anzahl an schwarzen Kanten
⇒ wird als k-Kreis bezeichnet
Kreisdekomposition C ist Aufteilung von G(π) in
kantendisjunkte Kreise
8/44

9. Beispiel
0 7 5 6 3 2 4 1 8
Figure : Kreisdekomposition von [7563241], Rot ist 3-Kreis, Schwarz ist
anderer 3-Kreis, Blau sind 1-er Kreise
9/44

10. Erste Beobachtungen
c2 : Anzahl an 2-Kreisen in Kreisdekomposition mit maximaler
Anzahl Kreisen
c3 : Anzahl restlicher Kreise mit Länge > 2
Satz 1
d(π) ≥ 2
3b(π) − 1
3 c2(π)
Beweis:
Bafna und Pevzner zeigten: d(π) ≥ b(π) − c2(π) − c3(π)
Jeder der c3 Kreise hat mindestens 3 schwarze Kanten:
c3 ≤ 1
3 (b(π) − 2c2(π))
d(π) ≥ b(π) − c2(π) −
1
3
(b(π) − 2c2(π))
=
2
3
b(π) −
1
3
c2(π)
10/44

11. Ziel, um 3/2 Approximation zu erreichen
3
2 mal die untere Schranke:
3
2
∗ (
2
3
b(π) −
1
3
c2(π)) = b(π) −
1
2
c2
⇒ Ziel ist es also maximal b(π) − 1
2 c2 Reversionen zu benötigen
11/44

12. Weitere Vorgehensweise
1 Ausgehend von einer Kreisdekomposition eine Vorgehensweise
finden
2 Eine ausreichend gute Kreisdekomposition finden
3 Beweisen, dass wir maximal b(π) − 1
2c2 Reversionen benötigen
12/44

13. Reversal Graph
Bezeichnet als R(C) mit C Kreisdekomposition
Jede grüne Kante in G(π) ist ein Knoten von R(C)
⇔ für jede gewollte Nachbarschaft gibt es Knoten
13/44

14. Beispiel(Knoten von R(C))
0 7 5 6 3 2 4 1 8
6-7
3-4
0-1
4-5
1-2
7-8
5-6
2-3
14/44

15. Reversal Graph
Bezeichnet als R(C) mit C Kreisdekomposition
Jede grüne Kante in G(π) ist ein Knoten von R(C)
⇔ für jede gewollte Nachbarschaft gibt es Knoten
Knoten v ist blau, wenn es die Pfeilspitze und den Schwanz
einer gerichtenten schwarzen Kante verbindet, ansonsten rot
Beispiel 3
a b c d a b c d
Figure : links: blauer Knoten in R(C), rechts: roter Knoten in R(C)
15/44

16. Beispiel(Farben der Knoten von R(C))
0 7 5 6 3 2 4 1 8
6-7
3-4
0-1
4-5
1-2
7-8
5-6
2-3
16/44

17. Reversal Graph
Bezeichnet als R(C) mit C Kreisdekomposition
Jede grüne Kante in G(π) ist ein Knoten von R(C)
⇔ für jede gewollte Nachbarschaft gibt es Knoten
Knoten v ist blau, wenn es den Kopf einer gerichteten
schwarzen Kante und den Schwanz einer schwarzen Kante
verbindet. Ansonsten rot.
Kante wird eingefügt, wenn diese sich "überschneiden"
Beispiel 4
a b c d
Figure : Kante zwischen (a − c), (b − d)
17/44

18. Beispiel(Kanten von R(C)
0 7 5 6 3 2 4 1 8
6-7
3-4
0-1
4-5
1-2
7-8
5-6
2-3
18/44

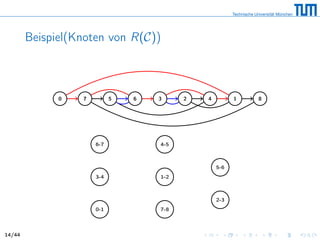
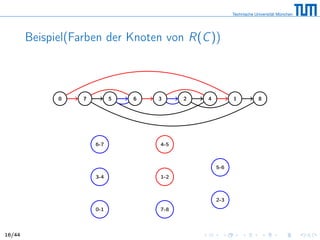
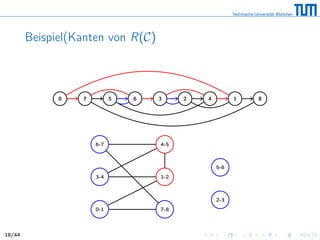
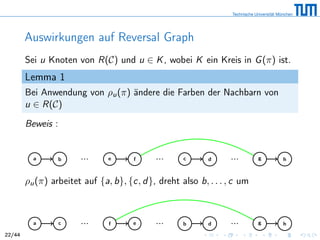
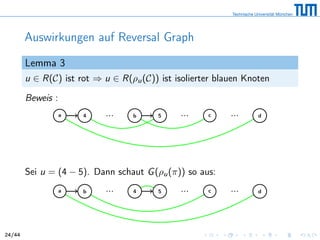
19. Auswirkungen von Reversionen
R(C) heißt Reversionsgraph, weil wir jedem Knoten v ∈ R(C)
Reversion zuweisen
Eine Reversion arbeitet immer auf zwei schwarzen Kanten
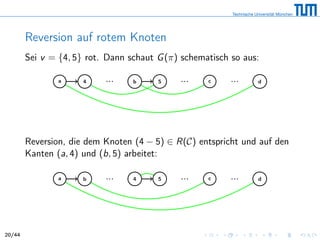
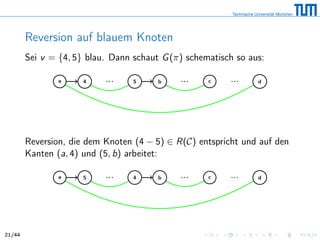
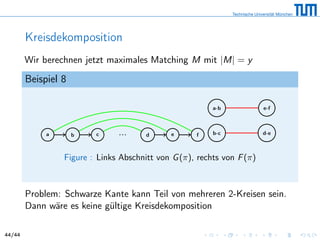
Beispiel 5
Reversion, die den schwarzen Kanten (5, 3) und (6, 4) zugeordnet ist:
[075 326
umdrehen
418] ⇒ [075 623
umgedreht
418]
19/44

20. Reversion auf rotem Knoten
Sei v = {4, 5} rot. Dann schaut G(π) schematisch so aus:
a 4 ... b 5 ... c ... d
Reversion, die dem Knoten (4 − 5) ∈ R(C) entspricht und auf den
Kanten (a, 4) und (b, 5) arbeitet:
a b ... 4 5 ... c ... d
20/44

21. Reversion auf blauem Knoten
Sei v = {4, 5} blau. Dann schaut G(π) schematisch so aus:
a 4 ... 5 b ... c ... d
Reversion, die dem Knoten (4 − 5) ∈ R(C) entspricht und auf den
Kanten (a, 4) und (5, b) arbeitet:
a 5 ... 4 b ... c ... d
21/44

22. Auswirkungen auf Reversal Graph
Sei u Knoten von R(C) und u ∈ K, wobei K ein Kreis in G(π) ist.
Lemma 1
Bei Anwendung von ρu(π) ändere die Farben der Nachbarn von
u ∈ R(C)
Beweis :
a b ... e f ... c d ... g h
ρu(π) arbeitet auf {a, b}, {c, d}, dreht also b, . . . , c um
a c ... f e ... b d ... g h
22/44

23. Auswirkungen auf Reversal Graph
Lemma 2
Sei u mit den Knoten v, w verbunden. Füge {v, w} hinzu, oder
lösche diese Kante bei Anwendung von ρu(π)
Beweis :
a b c d e f g h
ρu(π) wird ausgeführt, also c, . . . , f umgedreht
a b f e d c g h
23/44

24. Auswirkungen auf Reversal Graph
Lemma 3
u ∈ R(C) ist rot ⇒ u ∈ R(ρu(C)) ist isolierter blauen Knoten
Beweis :
a 4 ... b 5 ... c ... d
Sei u = (4 − 5). Dann schaut G(ρu(π)) so aus:
a b ... 4 5 ... c ... d
24/44

25. fertig, wenn nur noch 1-er Kreise/isolierte blaue Knoten
aus vorherigen Lemmata folgt, dass Reversionen nur Knoten in
der selben Zusammenhangskomponente verändern
Deshalb jetzt Einteilung von R(C) in
unorientierte Zusammenhangskomponenten: enthalten nur
blaue Knoten
orientierte Zusammenhangskomponenten: enthalten mind.
einen roten Knoten
Vorsicht: isolierte blaue Knoten werden in diese Einteilung nicht
aufgenommen, weil sie schon sortiert sind
25/44

26. Sei A Zusammenhangskomponente. Dann ist Au der Subgraph von
der alle unsortierten Knoten von A nach der Reversion ρu enthält
Lemma 4
Sei A orientierte Komponente und u ∈ A rot. Dann ist jede
Komponente von Au orientiert
Beweis : Sei u ∈ A rot. Angenommen es gibt unorientierte
Zusammenhangskomponente U in Au.
U muss also mindestens 2 blaue Knoten v, w haben.
u v w v u w
Links Typ 1, Rechts Typ 2
26/44

27. u v w v u w
Links Typ 1, Rechts Typ 2
Definitionen für den Beweis:
f (u) = v, ∀ roten Knoten u ∈ A
Folge u0 = u, ui+1 = f (ui )
Da es nur endlich viele rote Knoten gibt, ist die Folge zyklisch
(Teilfolge wird sich immer wieder wiederholen)
27/44

28. Angenommen wir befinden uns an beliegen Knoten us aus dem
Zyklus und us ist vom Typ 1:
us us+1 w
us+2
{us+1, w} ist Kante, aber {us, w} nicht
us+2 ist in einer unorientierten Komponente nach ρus+1 (π)
{us+2, w} muss Kante in A sein, da sonst w nach ρus+1 (π) rot
wäre und mit us+2 verbunden wäre
so kann man auch für us+3, us+4, . . . argumentieren, also
{us+i , w} in A
Widerspruch, da Folge zyklisch ist und dann {us, w} Kante wäre
28/44

29. Sei us = us+k im Zyklus. us kann also nur vom Typ 2 sein:
us+1 us w
us+k−1
{us, w}, {us, us+1} sind Kanten in A und {us+1, w} nicht
us ist in unorientierter Komponente nach ρus+k−1
(π)
{us+k−1, w} muss in A liegen da, da w sonst nach ρus+k−1
(π)
rot wäre und mit us verbunden wäre und us nicht in
unorientierter Zhgk liegen würde
selbes gilt für {us+k−2, w}, {us+k−3, w}, . . . , {us+i , w} in A
Widerspruch, da {us+1, w} nicht in A liegt
29/44

30. Satz 2
Sei v ein Knoten von R(C)
ρ(v) ist eine 2-Reversion genau dann wenn v auf orientiertem 2-er
Kreis liegt
Beweis : Orientierter 2-Kreis:
4 7 ... 5 8
Sowohl die Reversion (7 − 8), als auch (4 − 5) schauen so aus:
4 5 ... 7 8
30/44

31. Satz 3
Um orientierte Komponente C mit k Kreisen zu sortieren brauchen
wir genau k 2-Reversionen und sonst 1-Reversionen
Beweis :
Da C orientiert ist, hat er einen roten Knoten u
ρu(π) macht u zu isoliertem Knoten, ist also eine 1-Reversion
Wenn u aber Teil eines 2-Kreises ist, ist es eine 2-Reversion
Da Cu nur orientierte Komponenten enthält, können wir das
solange machen, bis die Komponente sortiert ist
Da wir k Kreise haben, brauchen wir k 2-Reversionen und sonst
1-Reversionen
31/44

32. Lemma 5
Sei A eine unorientierte Komponente. Dann ist Av eine orientierte
Komponente für alle v ∈ A
Beweis :
A unorientiert, hat also nur blaue Knoten
Nehme beliebigen Knoten v ∈ A.
Von vorher: alle Nachbarn von v ändern durch Anwendung von
ρv ihre Farbe
⇒ Av ist orientiert
32/44

33. Erstes Ergebnis
u(C) ist die Anzahl an unorientierten Komponenten.
Satz 4
d(π) ≤ b(π) − |C| + u(C)
Beweis :
b(π) wäre genau die Anzahl an Reversionen wenn wir nur
1-Reversionen hätten
pro unorientierte Komponente brauchen wir 1 Reversion, um sie
orientiert zu machen ⇒ +u(C)
jeder Kreis in C wird mal 2-Kreis sein
⇒ - |C|
33/44

34. Kreisdekomposition
Aus vorherigem Verfahren wissen wir, dass 1-Reversion immer
möglich ist
Also ist Ziel möglichst viele 2-Reversionen
⇒ möglichst viele 2-Kreise
Es wird nicht eingegangen, wie eine solche Dekomposition erstellt
wird.
34/44

35. Aussagen über Kreisdekomposition
Wir berechnen ein sogenanntes Matching M
M besteht aus y Leiter-2-Kreisen und z isolierten 2-Kreisen
Also |M| = y + z
Wir erreichen nur Kreisdekomposition mit y
2 + z 2-Kreisen
35/44

36. Beweis der oberen Schranke
Satz 5
Man kann π mit höchstens b(π) −
c2(π)
2
Reversionen sortieren
Beweis :
3 "Arten" von Komponenten:
u unorientierte Komponenten, die jeweils mindestens einen
Kreis länger als 2 und l 2-Kreise haben
⇒ Minimal l + u 2-Reversionen, u 0-Reversionen, sonst
1-Reversionen
v restliche unorientierte Komponenten, die nur m unorientierte
2-Kreise enthalten
⇒ Benötigt m 2-Reversionen und v 0-Reversionen
36/44

37. k der 2-Kreise sind in orientierten Komponenten
⇒ Diese Komponenten werden mit mindestens k 2-Reversionen
und sonst 1-Reversionen sortiert
Zusammen:
k + l + u + m 2-Reversionen
u + v 0-Reversionen
Rest 1-Reversionen
Von vorher: Maximal b(π) − |C| + u(C)
⇒ Maximal b(π) − k − l − m − u + u + v Reversionen
Es bleibt zu zeigen: k + l + m − v ≥
c2(π)
2
37/44

38. Es bleibt zu zeigen: k + l + m − v ≥ c2(π)
2
Aus Kreisdekomposition wissen wir:
1 |M| ≥ c2(π)
2 k + l + m = y
2 + z
3 Die v Komponenten haben nur Kreise aus den z isolierten
Kreisen
Daraus folgt, dass zu zeigen bleibt:
y
2
+ z − v ≥
|M|
2
38/44

39. Es bleibt zu zeigen: y
2 + z − v ≥ |M|
2
Die v Komponenten müssen jeweils aus mindestens 2 Kreisen
bestehen:
Beispiel 6
1 5 x 6 2
Wenn an Position x keine Knoten wären, wäre (5 − 6) ein 1-Kreis
und kein 2-Kreis
39/44

40. Es bleibt zu zeigen: y
2 + z − v ≥ |M|
2
die v Komponenten müssen aus mindestens 2 Kreisen bestehen
sie bestehen nur aus isolierten 2-Kreisen
⇒ v ≤
z
2
y
2
+ z − v ≥
y
2
+
z
2
|M|=y+z
≥
|M|
2
40/44

41. Komplexität
Satz 6
Berman, Karpinski haben bewiesen, dass jeder polynomielle
Approximationsalgorithmus höchstens eine Approximationsgüte von
1.008 oder schlechter, außer wenn P = NP
⇒ Min − SBR /∈ PTAS
41/44

42. Danke für eure Aufmerksamkeit!
Noch fragen?
42/44

43. Matchinggraph
Wir führen den Matchinggraph F(π) ein:
Knoten für jede schwarze Kante (i, i + 1)
Kante zwischen u, v ∈ F(π) wenn u, v mit ihren grünen Kanten
einen 2-Kreis geben
Beispiel 7
a c ... b d ... e g ... f h
Sowohl links als auch rechts gibt es Kante zwischen
(a − c), (b − d) ∈ F(π)
43/44

44. Kreisdekomposition
Wir berechnen jetzt maximales Matching M mit |M| = y
Beispiel 8
a b c ... d e f
a-b e-f
b-c d-e
Figure : Links Abschnitt von G(π), rechts von F(π)
Problem: Schwarze Kante kann Teil von mehreren 2-Kreisen sein.
Dann wäre es keine gültige Kreisdekomposition
44/44