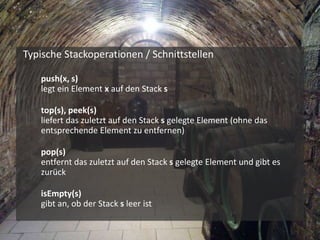
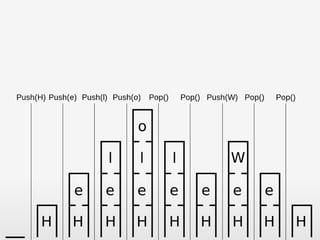
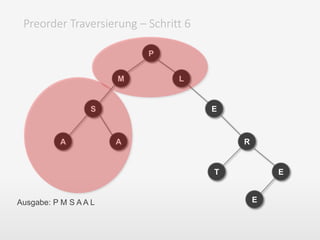
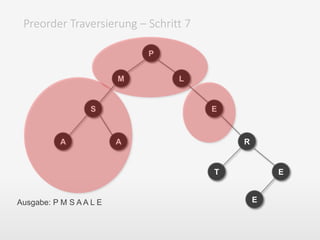
Das Dokument behandelt grundlegende Datenstrukturen wie Stacks, Queues und Listen sowie Algorithmen zur Datenmanipulation in C++ und JavaScript. Es werden wesentliche Unterschiede in der Programmierung, Typisierung, und dem Umgang mit Variablen erläutert, einschließlich einer Diskussion über Traversierungsarten und typische Operationen auf den jeweiligen Datenstrukturen. Außerdem wird der Minimierungsalgorithmus und das Konzept der Baumstruktur behandelt, einschließlich verschiedener Traversierungsstrategien.

1. Basisinformationstechnologie II – Sommersemester 2016 – 18. April 2016
Dr. Jan G. Wieners
Datenstrukturen
Stack, Queue, Liste, Graph

2. Differenzierung anhand von C++ und JavaScript:
 Compiler vs. Interpreter
 Typisierung !: Dynamisch vs. statisch
 Variablen: Deklaration vs. Initialisierung
 Paradigmen: funktionale vs. Objektorientierte
Programmierung
 Objektorientierung: Klassen, Kapselung, Geheimnisprinzip
 Hardwarenahe Programmierung: C++ und Zeiger
 Gemeinsamkeiten: Auswahlanweisungen und
Kontrollstrukturen
 Schichten-Architektur: MVC
WS15/16: Programmiersprachen und ihre Unterschiede

3. Datenstrukturen

4. Datenstrukturen
 Stack / Kellerspeicher
 Queue
 Liste
 Baum
 Traversierungsarten
 Preorder
 Inorder
 Postorder
 Levelorder
Such- und Sortieralgorithmen
Themenüberblick „Algorithmen und Datenstrukturen“

5. Datentyp:
 Bauplan für eine Variable (benannte Speicherstelle im
Arbeitsspeicher des Rechners)
 Legt fest, welche Operationen mit einer Variable möglich sind
 Bestimmt die interne Darstellung (Repräsentation) der
Variablen im Rechner
 Z.B. bool, int, float, double, unsigned int, etc.
Algorithmen, Datenstrukturen

6. Datenstruktur = Daten + Funktionen
Datenstrukturen:
 Stacks (Stapel)
 Queues
 Listen
 Einfach verkettete Listen
 Doppelt verkettete Listen
 Bäume
 Binärbäume
Algorithmen, Datenstrukturen

7. Stack / Kellerspeicher

8. Typische Stackoperationen / Schnittstellen
 push(x, s)
legt ein Element x auf den Stack s
 top(s), peek(s)
liefert das zuletzt auf den Stack s gelegte Element (ohne das
entsprechende Element zu entfernen)
 pop(s)
entfernt das zuletzt auf den Stack s gelegte Element und gibt es
zurück
 isEmpty(s)
gibt an, ob der Stack s leer ist

10. Queue / Warteschlange

11. LIFO?
FIFO?

12. Listen

14. Um die Liste zu durchlaufen:
 Beginn beim ersten Element („Anker“ für den Beginn der
Liste)
 „next“ zeigt auf das nächste Listenelement
 Letztes Glied der Kette: next-Zeiger = NULL
 Um wieder auf das erste Element zugreifen zu können:
anfang-Zeiger auf das erste Element der Liste
 Hilfszeiger auf innere Elemente: cursor
Einfach verkettete Liste

15. Element Einfügen:
 Ursprüngliche Liste:
 Liste nach Einfügen von Element „mat“
Einfach verkettete Liste
bat cat sat vat NULLstart
bat cat sat vat NULLstart
mat

16. Element Löschen:
 Ursprüngliche Liste:
 Liste nach Entfernen des Elements „cat“
Einfach verkettete Liste
bat cat sat vat NULLstart
bat cat sat vat NULLstart

17. Vorteil:
 Elemente lassen sich sehr schnell am Anfang der einfach
verketteten Liste einfügen
Nachteil:
 Über jedes einzelne Element muss iteriert werden
Einfach verkettete Liste
bat cat sat vat NULLstart

18. Charakteristika: Jedes Element verfügt über
 Einen Inhalt
 Einen Zeiger auf das nachfolgende Element
 Einen Zeiger auf das vorhergehende Element
Vorteile
 Möglichkeit, vom Ende der Liste zum Beginn zu iterieren
 Schnelles Löschen und Einfügen von Elementen
Nachteil
 Speicherplatzbedarf durch zweiten Zeiger erhöht
Doppelt verkettete Liste
bat cat sat vat NULLstart

19. Datenstrukturen √
 Stack / Kellerspeicher √
 Queue √
 Liste √
 Baum
 Traversierungsarten
Themenüberblick „Algorithmen und Datenstrukturen“

21. Extensivform von Spielen (Tic Tac Toe)

22. Der Minimax-Algorithmus
𝑥0
𝑥1 𝑥2
𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9 𝑥10 𝑥11 𝑥12
𝑥3
3 12 8 2 4 6 14 5 2
𝑠 𝑀𝐴𝑋1
𝑠 𝑀𝐴𝑋2
𝑠 𝑀𝐴𝑋3
MAX
MIN 3 2 2
3
min(3,12,8)=3
min(2,4,6)=2
max(3,2,2)=3
min(14,5,2)=2

23. Baum: Begrifflichkeiten
Bäume
Wurzel
Kante
Innerer Knoten / Kindknoten
Blatt

24. Traversieren  Jeden Knoten des Baumes besuchen
Reihenfolge, in der die Knoten besucht werden:
 Preorder, auch: „Hauptreihenfolge“ / Tiefensuche
 Inorder, auch: „symmetrische Reihenfolge“
 Postorder, auch: „Nebenreihenfolge“
 Levelorder, auch: „Breitensuche“
Traversierung

25. Rekursive Regel:
 besuche die Wurzel
 Besuche den linken Unterbaum
 Besuche den rechten
Unterbaum
 WLR
Preorder Traversierung
Quelle: http://de.wikipedia.org/w/index.php?title=Datei:Depth-First-Search.gif&filetimestamp=20090326120256 (MRE)

26. Preorder Traversierung – Schritt 0
P
M
S
A A
L
E
T
R
E
E

27. Preorder Traversierung – Schritt 1
P
M
S
A A
L
E
T
R
E
EAusgabe: P

28. Preorder Traversierung – Schritt 2
P
M
S
A A
L
E
T
R
E
EAusgabe: P M

29. Preorder Traversierung – Schritt 3
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S

30. Preorder Traversierung – Schritt 4
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A

31. Preorder Traversierung – Schritt 5
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A

32. Preorder Traversierung – Schritt 6
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L

33. Preorder Traversierung – Schritt 7
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L E

34. Preorder Traversierung – Schritt 8
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L E R

35. Preorder Traversierung – Schritt 9
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L E R T

36. Preorder Traversierung – Schritt 10
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L E R T E

37. Preorder Traversierung – Schritt 11
P
M
S
A A
L
E
T
R
E
EAusgabe: P M S A A L E R T E E

38. Datenstrukturen √
 Stack / Kellerspeicher √
 Queue √
 Liste √
 Baum √
 Traversierungsarten √
 Preorder √
 Inorder √
 Postorder √
 Levelorder √
Such- und Sortieralgorithmen
Themenüberblick „Algorithmen und Datenstrukturen“

39. /

40.  https://commons.wikimedia.org/wiki/File:Universitat_
zu_Koln_Hauptgebaude_ost.jpg
 https://de.wikipedia.org/wiki/Imbiss
 https://commons.wikimedia.org/wiki/File:Sklep_cejkov
ice.JPG
Bildnachweise