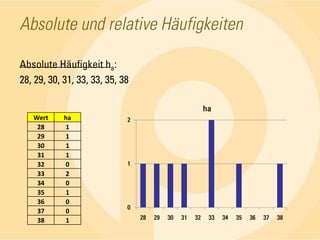
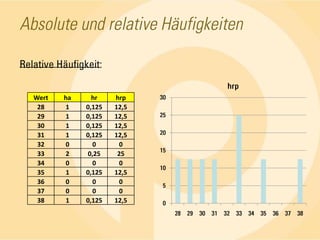
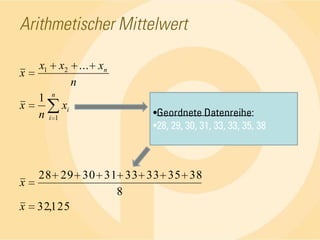
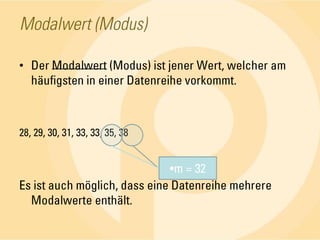
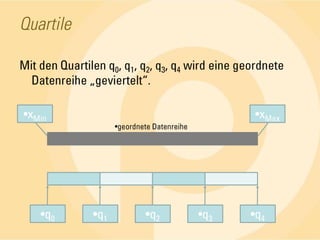
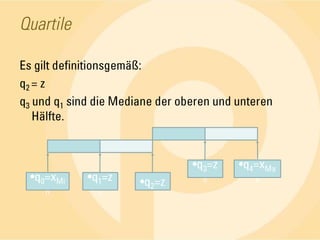
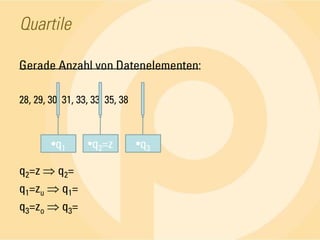
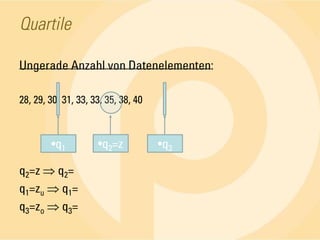
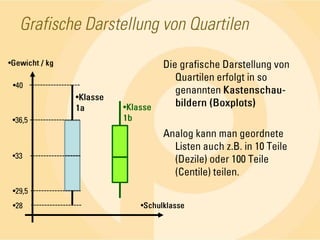
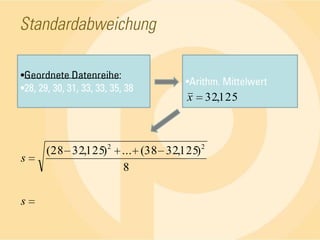
Das Dokument behandelt statistische Grundlagen, insbesondere die deskriptive und induktive Statistik sowie deren Methoden zur Analyse und Darstellung von Daten. Es erläutert wichtige Begriffe wie absolute und relative Häufigkeiten, arithmetisches Mittel, Median, Modalwert, Quartile und Standardabweichung anhand von Beispielen. Die Anwendung dieser Konzepte wird in verschiedenen Fällen, wie der Untersuchung von Seminargruppen, verdeutlicht.

1. Statistik und Wahrscheinlichkeit 1LV-Leiter: Arno Raunegger

2. StochastikStatistikWahrscheinlich-keitstheorieDeskriptive (beschreibende) StatistikInduktive (schließende) Statistik

3. Begriffsklärung 1Deskriptive Statistik: Ausgangspunkt sind Daten, die inihrer Rohform oft als Urlisten vorliegen. Meistens sinddiese Daten sehr umfangreich und im Einzelnen garnicht mehr überblickbar.Um die Daten systematisch zu ordnen,zu charakterisieren und übersichtlichdarzustellen wendet man die Methodender beschreibenden Statistik an.

4. Begriffsklärung 2Häufig wird in statistischen Erhebungen eine bestimmte Grundgesamtheit (eine z.B. Anzahl von Personen mittels Fragebogen) hinsichtlich bestimmter Variablen (Merkmale) befragt. Beispiele dazu sind:

5. Ungeordnete/Geordnete DatenreiheBsp.: Gewicht von Schülern in einer SchulklasseUngeordnete Datenreihe (Urliste):38, 29, 33, 31, 35, 30, 28, 33Geordnete Datenreihe:28, 29, 30, 31, 33, 33, 35, 38Variable (Merkmal)Variablenwerte (Merkmalsaus-prägungen)

6. Absolute und relative HäufigkeitenAbsolute Häufigkeit ha:28, 29, 30, 31, 33, 33, 35, 38

7. Absolute und relative HäufigkeitenRelative Häufigkeit:Relative Häufigkeit in Prozent:

8. Absolute und relative HäufigkeitenRelative Häufigkeit:

9. Anwendungsbeispielea) Geschlecht Seminargruppe: => Absolute, relative und prozentuelle Häufigkeit => Säulen- und Kreisdiagrammb) Zweitfachverteilung Seminargruppe: => Absolute, relative und prozentuelle Häufigkeit => Säulen- und Kreisdiagramm

10. Spannweite, Minimum und MaximumGeordnete Datenreihe:28, 29, 30, 31, 33, 33, 35, 38Spannweite: R = xMax - xMinR =xMinxMax

11. Arithmetischer MittelwertGeordnete Datenreihe:28, 29, 30, 31, 33, 33, 35, 38

12. Modalwert (Modus)Der Modalwert (Modus) ist jener Wert, welcher am häufigsten in einer Datenreihe vorkommt.28, 29, 30, 31, 33, 33, 35, 38Es ist auch möglich, dass eine Datenreihe mehrere Modalwerte enthält.m = 32

13. Median (Zentralwert)Der Median (Zentralwert) teilt eine sortierte Datenreihe in genau zwei Hälften.28, 29, 30, 31, 33, 33, 35, 38Bei einer geraden Anzahl von Elementen in einer geordneten Datenreihe, ergibt sich der Median aus dem arithmetischen Mittelwert der beiden zentralen Elemente.z = 32

14. Median (Zentralwert)Ungerade Anzahl von Datenelementen:28, 29, 30, 31, 33, 33, 35, 38, 40Bei einer ungeraden Anzahl von Elementen in einer geordneten Datenreihe, ergibt sich der Median genau aus dem mittleren Element.xMed=33

15. Robustheit von ZentralmaßenGehaltsstruktur in einer Firma:1000, 1000, 1200, 1200, 1200, 1200, 1500, 4000„Ausreißer“ bereinigen:1000, 1000, 1200, 1200, 1200, 1200, 1500, 4000x = z = m = x = z = m =

16. QuartileMit den Quartilen q0, q1, q2, q3, q4 wird eine geordnete Datenreihe „geviertelt“.xMinxMaxgeordnete Datenreiheq0q1q2q3q4

17. QuartileEs gilt definitionsgemäß: q2 = zq3 und q1 sind die Mediane der oberen und unteren Hälfte.q3=zoq4=xMaxq0=xMinq1=zuq2=z

18. QuartileGerade Anzahl von Datenelementen:28, 29, 30, 31, 33, 33, 35, 38q2=z  q2=q1=zu q1=q3=zo q3=q2=zq3q1

19. QuartileUngerade Anzahl von Datenelementen:28, 29, 30, 31, 33, 33, 35, 38, 40q2=z  q2=q1=zu q1=q3=zo q3=q2=zq3q1

20. Grafische Darstellung von QuartilenDie grafische Darstellung von Quartilen erfolgt in so genannten Kastenschau-bildern (Boxplots)Analog kann man geordnete Listen auch z.B. in 10 Teile (Dezile) oder 100 Teile (Centile) teilen.Gewicht / kg40Klasse 1aKlasse 1b36,53329,5Schulklasse28

21. StandardabweichungDie Standardabweichung s ist ein Maß für die Streuung der Merkmalswerte xi um den arithmetischen Mittelwert .

22. StandardabweichungGeordnete Datenreihe:28, 29, 30, 31, 33, 33, 35, 38Arithm. Mittelwert

23. VarianzDie Standardabweichung s ergibt sich aus der Quadratwurzel der Varianz, daher gilt für die Varianz:Häufig ist in der Literatur auch folgende Formel zu finden:Stichproben-umfang „Ausreißer bereinigt“