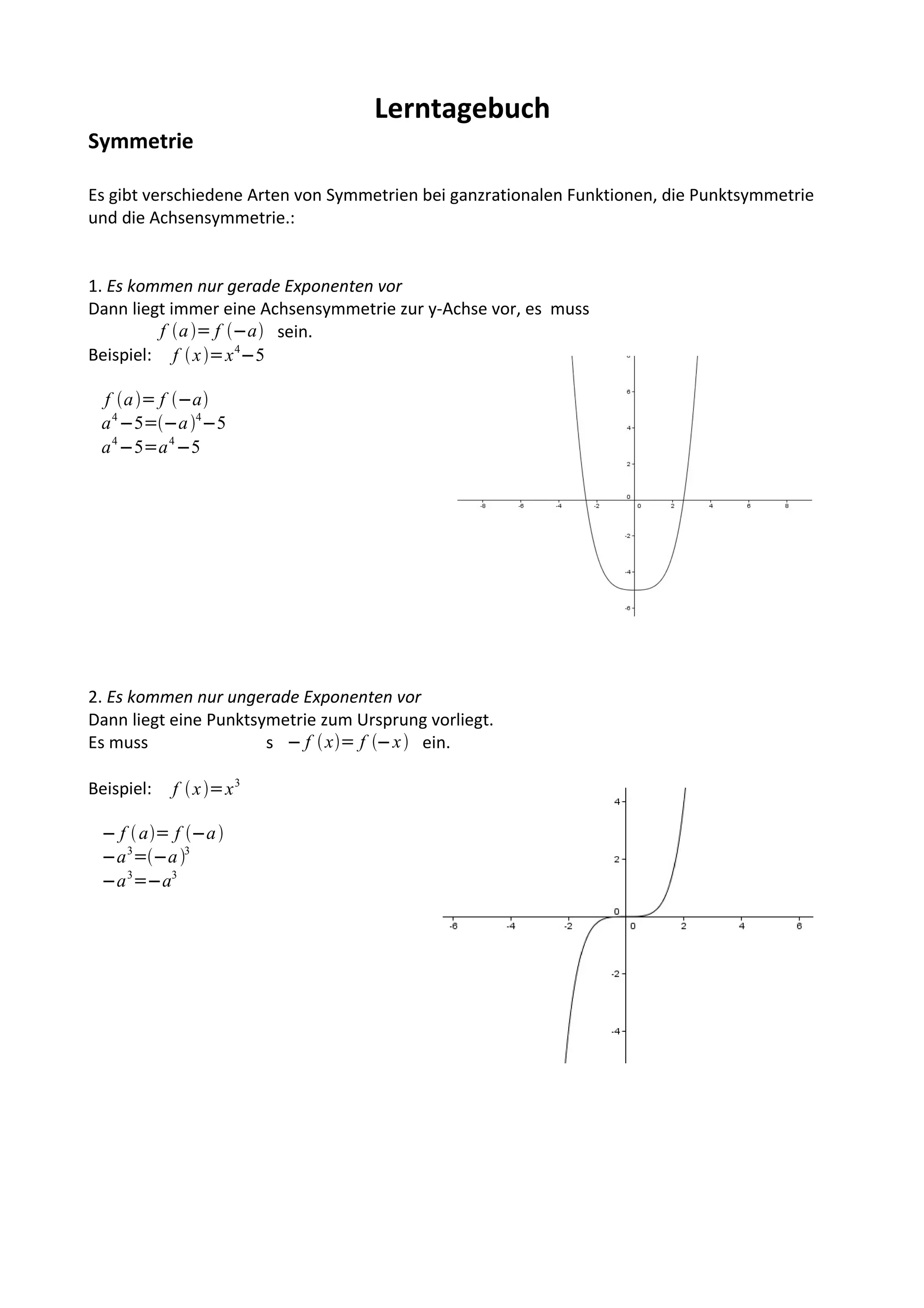
Das Dokument behandelt Symmetrien bei ganzrationalen Funktionen, insbesondere Punkt- und Achsensymmetrie, sowie die Polynomdivision zur Bestimmung von Nullstellen. Zudem wird das Verhalten im Unendlichen von Funktionen in Abhängigkeit vom höchsten Exponenten und dem Koeffizienten erörtert. Schließlich werden Funktionenscharen erklärt, wobei Parameter den Verlauf und die Interaktion der Parabeln beeinflussen, ohne die Grundstruktur zu verändern.

1. Lerntagebuch
Symmetrie
Es gibt verschiedene Arten von Symmetrien bei ganzrationalen Funktionen, die Punktsymmetrie
und die Achsensymmetrie.:
1. Es kommen nur gerade Exponenten vor
Dann liegt immer eine Achsensymmetrie zur y-Achse vor, es muss
f a = f −a sein.
Beispiel: f  x =x 4−5
f a = f −a
a 4 −5=−a 4−5
a 4 −5=a 4 −5
2. Es kommen nur ungerade Exponenten vor
Dann liegt eine Punktsymetrie zum Ursprung vorliegt.
Es muss s − f  x= f −x  ein.
Beispiel: f  x =x 3
− f  a= f −a 
−a 3=−a 3
−a 3=−a3

2. Polynomdivision
Die Polynomdivision braucht man um 2 Polynome zu teilen. Es ist ähnlich wie die schriftliche
Division. Zum Beispiel:
(x³-15x²+71x-105):(x-5)=
1.Jetzt teilt man die höchste Potenzen,also x³:x=x²
(x³-15x²+71x-105):(x-5)=x²
2.Dann multipliziert man das x² mit dem Divisor (x-5)=x³-5x² und schreibt das unter den
Dividenten.
(x³-15x²+71x-105):(x-5)=x²
-(x³-5x²)
3.dann zieht man man das was unter dem Dividenten steht vom Dividenten ab
(x³-15x²+71x-105):(x-5)=x²
-(x³-5x²)
-10x²+71x
4.Mit dem Ereignis der Subraktion wird dies jetzt wiederholt:
(x³-15x²+71x-105):(x-5) = x²-10x+21
-(x³-5x²)
-10x²+71x
-(-10x²+50x)
21x-105
-(21x-105)
0
Diese Polynomdivision braucht man z.B. um die Nullstellen von einem Polynom rauszukriegen,
indem man es mit dieser Methode in seine Linearfaktoren zerlegt( da kann man die Nullstellen ja
dann ablesen). Dazu muss man eine Nullstelle mit dem GTR bestimmen und dann durch x-
Nullstelle teilen.

3. Das Verhalten im Unendlichen
Das Verhalten im Unendlichen is abhängig vom größten Exponent und dem Koeffizient vor diesem.
Es gibt 4 Fälle:
Größter Exponent gerade Größter Exponent ungerade
Koefizient positiv Für x →∞ strebt f  x →∞ Für x →∞ strebt f  x →∞
Für x →−∞ strebt f  x →∞ Für x →−∞ strebt f  x →−∞
Koeffizient negativ Für x →∞ strebt f  x →−∞ Für x →∞ strebt f  x →−∞
Für x →−∞ strebt f  x →−∞ Für x →−∞ strebt f  x →∞
Ob die anderen Exponenten positiv oder negativ sind ist egal.
Funktionenscharen
1. f  x =x² 2xt
Das t (Parameter) verändert den Schnittpunkt der Parabel mit der y-Achse, den Achsen-Abschnitt.
An der Form der Parabel ändert sich nichts.
1.
2. f  x =tx² 3
t streckt bzw. staucht die Parabel während der y-Achsen-Abschnitt gleich bleibt.2.
2.
3. f  x =x² tx1
Der Scheitel verändert sich während der y-Achsen-Abschnitt gleicht bei 1 bleibt.