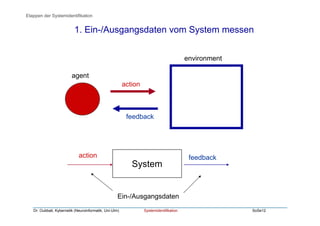
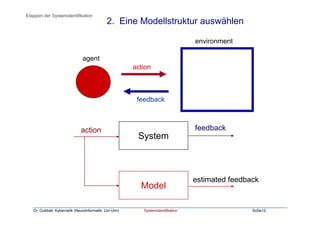
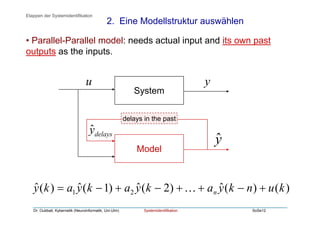
Das Dokument behandelt die Systemidentifikation, die Methoden und Algorithmen umfasst, um aus gemessenen Ein- und Ausgangsdaten empirische Modelle eines Systems zu erstellen. Es beschreibt die Schritte der Systemidentifikation, darunter das Messen der Daten, Auswahl der Modellstruktur, Anpassung der Parameter und Validierung des Modells. Verschiedene Modellstrukturen wie AR, MA und ARMA sowie Methoden zur Parameteranpassung wie die Methode der kleinsten Quadrate werden erläutert.

1. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Kybernetik
Systemidentifikation
12. 06. 2012
Mohamed Oubbati
Institut für Neuroinformatik
Tel.: (+49) 731 / 50 24153
mohamed.oubbati@uni-ulm.de

2. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
?
Was ist Systemidentifikation?
Der Begriff Systemidentifikation beschreibt Methoden und Algorithmen, die
aus gemessenen Ein-/Ausgangsdaten vom System, ein empirisches
Modell des Systems erzeugen.
Input/output u(n) /y(n) data Systemidentifikation empirisches Modell
)(ky)(ku

3. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Etappen der Systemidentifikation

4. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Etappen der Systemidentifikation
1. Ein-/Ausgangsdaten vom System messen.
2. Modellstruktur auswählen (AR, ARMA, …).
3. Parameter des Modells anpassen.
4. Das gefundene Modell validieren (prüfen).
Etappen der Systemidentifikation

5. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
1. Ein-/Ausgangsdaten vom System messen
agent
environment
action
feedback
System
action feedback
Etappen der Systemidentifikation
Ein-/Ausgangsdaten

6. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
1. Ein-/Ausgangsdaten vom System messen
System
feedback
Etappen der Systemidentifikation
Anregungssignal
Anregungssignale, mit denen das System (agent-
environment) angeregt wird, spielen eine große Rolle bei
dem Identifikationsverfahren. Es ist dabei wichtig ein
möglichst breites Frequenzspektrum abzudecken.

7. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Anregungssignale zur Systemidentifikation
Dies kann mithilfe verschiedener Eingangssignale produziert:
• Impuls: eher für die theoretische Analyse hilfreich.
• Sinus-Sweep: Sinusschwingung mit ständig ansteigender Frequenz.
• Rauschen: können als regelmäßige Sprünge verschiedener Amplitude
erstellt werden.
• PRBS (Pseudo Random Binary Signal): können als eine Folge von
Rechteckimpulsen unterschiedlicher Länge erstellt werden.
1. Ein-/Ausgangsdaten vom System messen
Etappen der Systemidentifikation

8. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
2. Eine Modellstruktur auswählen
Etappen der Systemidentifikation
agent
environment
action
feedback
System
action feedback
Model
estimated feedback

9. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Model
u y
• AR-Modell
Bei AR-Modellen benutzt man eine spezielle Regressionsgleichung die
Autoregressionsgleichung (kurz: AR).
• MA-Modell
Das MA-Modell “Moving-Average” (kurz: MA) beschreibt die
Abhängigkeitsbeziehungen der Inputs wie folgt:
2. Eine Modellstruktur auswählen
Etappen der Systemidentifikation
)()2()1()( 21 nkyakyakyaky n −++−+−= K
)()1()()( 1 mkubkubkuky m −+−+= K

10. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Model
u y
• ARMA-Modell
AR-Modelle und MA-Modelle verknüpft ergeben eine sehr nützliche Klasse von
Zeitreihenmodellen, die ARMA-Modelle:
2. Eine Modellstruktur auswählen
Etappen der Systemidentifikation
)()1()(
)()2()1()(
1
21
mkubkubku
nkyakyakyaky
m
n
−+−++
−++−+−=
K
K

11. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
2. Eine Modellstruktur auswählen
Etappen der Systemidentifikation
• Series-Parallel model: needs actual input and past output of the
system as input to the model.
System
Model
u y
delays in the past
ydelays
yˆ
)()()2()1()(ˆ 21 kunkyakyakyaky n +−++−+−= K

12. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
2. Eine Modellstruktur auswählen
Etappen der Systemidentifikation
• Parallel-Parallel model: needs actual input and its own past
outputs as the inputs.
)()(ˆ)2(ˆ)1(ˆ)(ˆ 21 kunkyakyakyaky n +−++−+−= K
System
Model
u y
yˆ
delays in the past
delaysyˆ

13. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
System
Model
u y
yˆ
3. Parameter des Modells anpassen
Etappen der Systemidentifikation
Ist eine Modellstruktur gefunden, so muss noch eine
Parameteranpassung vorgenommen werden. Dies wird
erreicht, sodass die Differenz zwischen dem realen System
und dem ausgewählten Modell so klein wie möglich sein soll.

14. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
3. Parameter des Modells anpassen
Etappen der Systemidentifikation
System
y
yˆ
+
-
Parameteranpassung
Methode
Model
u
ia ib,( )
Methoden zur Parameteranpassung
- Least Squares (LS)
- Recursive Least Squares (RLS)
- Prediction Error Method (PEM)
- Recursive Prediction Error Method (RPE)
- Artificial Neural Networks
- …
yy ≈ˆ
ia ib,
sodass
?

15. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Methode der kleinsten Quadrate
(Least Squares Method)
3. Parameter des Modells anpassen

16. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Die Modellstruktur des Systems wird als ARMA-Modell in Serie-Parallel
Form ausgewählt.
Methode der kleinsten Quadrate
System
Model
u y
delays in the past
ydelays
yˆ
)()1()(
)()2()1()(ˆ
1
21
mkubkubku
nkyakyakyaky
m
n
−+−++
−++−+−=
K
K
delays
in the past ia ib,( )
3. Parameter des Modells anpassen

17. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Unbekannt!
( )n
T
aaaa ,,, 21 K=
( )m
T
bbbb ,,, 21 K=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
b
a
θ
( ))(,),2(),1( mkukukuU T
−−−= K
( ))(,),2(),1( nkykykyY T
−−−= K
• Messdaten
• Parameter
Nk ,,2,1 K=
Methode der kleinsten Quadrate
3. Parameter des Modells anpassen
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
U
Y
k )(ϕ
θϕ )()(ˆ kky T
=
• Die Vorhersage des Modells im Zeitpunkt k
Nk ,,2,1 K=

18. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
θϕθξ )()()(ˆ)(),( kkykykyk T
−=−=
• Die Differenz zwischen den gemessenen Ausgangswerten und den
Ausgangswerten des Modells ist
)(ky
)(ˆ ky
• Die Aufgabe der systemidentifikation ist es, der Vektor (eine
Approximation von ) zu finden, sodass
θˆ
Methode der kleinsten Quadrate
3. Parameter des Modells anpassen
θ
0ˆ)()(ˆ)ˆ,( ≈−= θϕθξ kkyk T

19. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
Das Least-Square Algorithm versucht eine Approximation zu finden,
durch die Minimierung der Funktion
θˆ
)(θNV
Methode der kleinsten Quadrate
3. Parameter des Modells anpassen
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
= ∑∑ =
−
=
N
k
N
k
T
kykkk
1
1
1
)()()()(ˆ ϕϕϕθ
( )∑=
=
N
k
N kV
1
2
,
2
1
)( θξθ
)(minargˆ θθ
θ
NV=

20. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Systemidentifikation SoSe12
4. Das gefundene Modell validieren (prüfen).Etappen der Systemidentifikation
System
Model
u y
yˆ
+
-
)(ˆ)()( kykyk −=ξ
∑=
=
N
K
N k
N
m
1
)(
1
ξ
( )
2
1
)(
1
∑=
−=
N
k
NN mk
N
Var ξ
∑=
=
N
K
N k
N
MSE
1
2
)(
1
ξ
Following statistics are often used for model validation
• mean error:
• variance:
• mean square error: