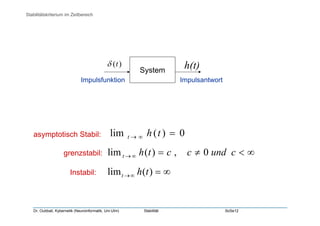
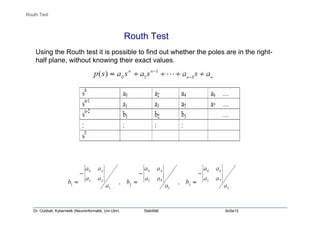
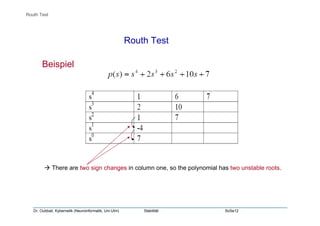
Das Dokument von Dr. Oubbati behandelt das Thema 'Stabilität' in der Kybernetik und Neuroinformatik. Es enthält Definitionen verschiedener Stabilitätsarten wie BIBO-Stabilität, asymptotische Stabilität, Grenzstabilität und Instabilität sowie Kriterien zur Bestimmung der Stabilität im Zeit- und Laplace-Bereich. Darüber hinaus wird das Routh-Testverfahren zur Analyse der Stabilität von Systemen erläutert.

1. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Kybernetik
Stabilität
22. 05. 2012
Mohamed Oubbati
Institut für Neuroinformatik
Tel.: (+49) 731 / 50 24153
mohamed.oubbati@uni-ulm.de

2. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Ein System, das nach einer Anregung in seinen ursprünglichen
Zustand von selbst zurückkehrt, heißt stabil.
Definition 1
Definitions
Stabilität

3. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
System
u y
Ein System heißt stabil, wenn für jedes begrenztes Eingangssignal u das
entsprechende Ausgangssignal y ebenfalls begrenzt bleibt.
ℜ∈21 , kkdie Konstanten
1ku ≤ 2ky ≤⇒
Definition 2 (BIBO-stability) (BIBO= Bounded Input Bounded Output)
Definitions
Stabilität

4. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Definition 3
Ein System, das nach
einer Anregung in
seinen ursprünglichen
Zustand von selbst
zurückkehrt, heißt
asymptotisch Stabil.
(asymptotically stable) (instable) (marginally stable)
Ein System, das nach
einer Anregung nicht in
seinen ursprünglichen
Zustand zurückkehrt, aber
begrenzt bleibt, heißt
grenzstabil.
Ein System, das nach
einer Anregung nicht
begrenzt bleibt, heißt
instabil.
Definitions
Stabilität

5. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Stabilitätskriterium im Zeitbereich

6. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
asymptotisch Stabil: 0)(lim =∞→ tht
grenzstabil: ∞<≠=∞→ cundcctht 0,)(lim
Instabil: ∞=∞→ )(lim tht
System
h(t)
Impulsfunktion Impulsantwort
)(tδ
Stabilitätskriterium im Zeitbereich

7. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Stabilitätskriterium im Laplace-Bereich

8. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
H(s)U Y
System
Stabilitätskriterium im Laplace-Bereich
H(s): Übertragungsfunktion
H(s)=
Zählerpolynom
Nennerpolynom
- Nennerpolynom heißt auch das charakteristische Polynom.
- Polstellen der Übertragungsfunktion sind die Nullstellen des Nennerpolynoms.
- Polstellen können komplex oder reell sein.
- die Polstellen der Übertragungsfunktion beeinflussen die Stabilität
und das Verhalten des LTI-Systems insgesamt.

9. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
asymptotisch Stabil: wenn alle Realteile der Polstellen absolut Negative sind.
isi ∀< ,0)Re(
grenzstabil: wenn mindestens eine Polstelle imaginär ist, bzw. das
Realteil=0.
Instabil: wenn mindestens eine Polstelle einen positiven Realteil hat.
si sind die Polstellen
( ) isi ∀≤ ,0Re
Stabilitätskriterium im Laplace-Bereich

10. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Grenzstabil Instabil
σ
jw
S-Ebene
Poles
σ
jw
S-Ebene
Poles
σ
jw
S-Ebene
Poles
asymptotisch Stabil
wenn alle Polstellen in der
linken S-Halbebene
liegen
wenn mindestens eine
Polstelle auf der j- Achse
liegt, und keine Polstelle in
der rechten s-Halbebene
liegt.
wenn mindestens
eine Polstelle auf der
rechten s-Halbebene
liegt
Stabilitätskriterium im Laplace-Bereich

11. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Routh Test

12. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Routh Test
Using the Routh test it is possible to find out whether the poles are in the right-
half plane, without knowing their exact values.
Routh Test

13. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Routh Theorem. The number of roots of p(s) in the right-
half plane equals the number of sign changes in the first
column.
Routh Test
Paper
Ming-Tzu Ho, Aniruddha Datta, and S. P. Bhattacharyya, An Elementary Derivation of the Routh–
Hurwitz Criterion, IEEE Transactions on Automatic Control vol. 43, no. 3, 1998, pp. 405-409.
Routh Test

14. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Beispiel
There are two sign changes in column one, so the polynomial has two unstable roots.
Routh Test
Routh Test

15. Dr. Oubbati, Kybernetik (Neuroinformatik, Uni-Ulm) Stabilität SoSe12
Treffen Sie eine Aussage über die Stabilität der folgenden Systeme:
88
1
)( 235
−−+
=
sss
sH
sss
sH
134
1
)( 23
++
=
2420105
1
)( 234
++++
=
ssss
sH
Routh Test