In diesem Bericht wird die Entwicklung eines parallelen und objektorientierten Simplex-Algorithmus zur Lösung von linearen Programmen (LPs) beschrieben, der auf dem Cray T3D Rechner implementiert wurde. Die Arbeit behandelt die numerische Stabilität der Algorithmen und zeigt Verbesserungen bei der Effizienz und Stabilität der Implementierungen durch den Einsatz spezieller Datenstrukturen und Techniken. Neben der sequentiellen Version werden auch parallele Implementierungen vorgestellt, die beschleunigte Lösungen für dünnbesetzte lineare Gleichungssysteme bieten.
















![letu
er Anfang der Lnearen Programmerung als mathematsche Disziplin läßt sch genau auf
das Jahr 1947 datieren, in dem G.B. Dantzig das erste Lneare Programm (LP) aufstellte
und den Smplex-Algorthmus als Lösungsverfahren formulierte. Zu dieser Zeit verwendete
man den Begriff Programm noch nicht in sener heutigen Bedeutung als Ausführungscode
für Computer. Vielmehr verstanden d e Mlitärs unter einem Programm enen Plan zur
Ressourcenverteilung; das erste von G.B. antzi aufgestellte Lineare Programm war eben
militärisches Planungsroblem.
Berets vor 1947 gab es verenzelte Arbeiten, heute der Lnearen Programmerung
zugeordnet werden müssen. Se bleben jedoch ohne Auswrkung auf die F o r t e n t w l u n g
der Mathematik w e die Arbeiten von Fourier 1823 und de la Vallee Poussin 1911, oder
wurden aus polsch-ideologischen Gründen ncht vorangetrieben (Kantorovch 193) [32]
neare Programme snd O e r u n g s r o b l e m e , d e Form
min cTx
s.t. Ax b,
x
gebracht werden önnen Dabei i t A ne Matr und c, b und x snd mensionskompatible
Vektoren. Schon bald stellte sich heraus, daß Lineare Programme weitreichende Anwen-
dungen n zahlreichen wirschaftlchen und gesellschaftlichen Gebieten haben, wi bei der
Transport- und Netzwerkpanung, der Ressourcenvertelung oder be Scheduling, um nu
nige zu nennen. 1949 faßte R Dorfman dese Gebite mit dem Begriff der mathematischen
Programmierung zusammen [32]. E n zentraler Tel davon ist die Lineare Programmerung,
deren Gegenstand die algorthmische Lösung von LPs ist. Solche treten oft bei der Lösung
mathematscher Programme auf. Dabei dient der (im Laufe der Zeit weiterentwickelte
Simplex-Algorthums bis heute als „Arbetspferd". Die heutige Bedeutung von LP-Lösern
zegt sch z.B. darin, daß 1995 mindestens 9 verschiedene Implementierungen kommerzell
angeboten wurden [88]
Obwohl n vielzählgen Anwendungen bewährt, der Splex-Algorthmus besonders
für Mathematiker nicht zufriedenstellend. Dies liegt daran, daß seine Laufzeit ncht be-
friedigend beschränt werden kann. Berets in den 50er Jahren wurde von A J . Hoffman
n LP angegeben, für das der damalige Splex-Algorthmus nicht terminier [65] Dieses](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-17-320.jpg)
![Einleitung
Problem des sog. K i n s konnte zwar durch spezelle Varianten umgangen werden ür
die meisten solcher Varanten gibt es aber Problembeispiele, die ein nicht polynomales
Laufzeitverhalten aufwesen. Alle bekannten Beispiele werden in [2] nhetlch zusammen-
gefaßt. Be vielen praktischen Problemen zeigt sch hingegen ne polynomale Laufzeit, was
auch durch statstsche Analysen untermauert werden kann [1]. Ob es jedoch polynomiale
Simplex-Algorthmen gibt, ist eine b s heute ffene Frage 70, 104]
eshalb wurde lange der Frage nachgegangen, ob Lneare Programme überhau po-
lynomaler Zeit gelöst werden können Diese Frage wurde 1979 von L.G. Khachian durch
Angabe der Ellipsoid-Methode positv beantwortet [69, 54]. Trotz ihrer theoretsch überle-
genen Laufzeit konnte die Ellipsoid-Methode oder deren Varianten in realen Anwendungen
ncht mit dem Simplex-Algorthmus konkurieren, und so beschränte sch die Fortentwick
lung der Linearen Programmerung noch wetere fünf Jahre iw. auf Verbesserungen des
Simplex-Verfahrens.
Viellecht durch die Ellipsod-Methode angespornt, stellte N . Karmarkar Jahr
1984 m t einem Innere-Punte-Verfahren einen anderen polynomalen LP-Löser vor [67]
nnere-Punkte-Verfahren wurden bereits set den 60er Jahren zur Lösung nichtlnearer Op
imerungsrobleme eingesetzt [44], jedoch wurden sie erst set 1984 für den lnearen Fall
ezialisiert und seither zu ner mächtigen Konkurrenz zu Splex-Algorithmen fortent-
kelt [76, 87]. Derzeit snd die Innere-Punkte-Verfahren und der Simplex-Algorithmus
glechermaßen etablert, und für viele Anwendungen ist ene Kombinaton beider Metho-
den mttels eines sog. Crossovers e beste Wahl [ 16]
Unabhängg von den Erfolgen der nnere-Punte-Verfahren komm dem implex-
Algorithmus auf absehbare Z i t ene nicht zu vernachlässgende Bedeutung zu. So liefert er
zusätzlich zu einer optimalen Lösung des LPs weitere Informationen wie die Schattenpreise,
die, ökonomisch nterpretiert, eine bessere Beurtelung der Lösung erlauben Darüberhn-
aus werden Splex-Algorthmen n Schnittebenen-Verfahren zur Lösung ganzzahliger Op-
timierungsprobleme eingesetzt. abei wrd eine Folge von jeweils leicht modifizierten LPs
generiert und gelöst. Nur der Splex-Algorthmus ist hierbei in der Lage, auf dem Ergeb-
n s des vorigen LPs aufzusetzen, um das jeweils neue LP schneller zu lösen Deshalb blebt
e Weiterenticklung des Smplex-Algorthmus' ein ständig atuelles Forschungsthema.
Di Verbesserungen des S l e x - A l g o r t h m u s ' haben se sener Erfindung Beachtlches
zustandegebracht. 1953 feierte man die Lösung eines 48 x 72 LPs noch mit Wein und
Schmaus [65 Heute werden auch LPs mit über 100000 Z l e n und Spalten routinemäßig
gelöst, und die Entwicklung immer ausgeklügelterer Verfahren, mit denen immer größere
LPs m immer kürzerer Ze gelöst werden können, ält weter an. Auch ie vorliegende
Arbet trägt dazu be
G.B. Dantzig formulerte den Splex-Algorithmus m t dem sog. Simplex-Tleau Dies
im wesentlchen eine Matrix, d e n jeder Iteration des Algorthmus' vollständg aktua
siert wrd. E n bedeutender Meilenstein be der Entwicklung des Simplex-Algorthmus'
bestand n der Formulierung des revidierten mplex-Algorthmus', be dem mmer nur ei](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-18-320.jpg)
![Einleitung
l des Tableaus, d e sog. B a s s m a t r i , aktualiert wrd Dafür üssen pro teraton zwe
Gleichungssysteme mit der Bassmatrx gelöst werden ennoch kann gezegt werden, daß
der Gesamtaufwand geringer ausfällt.
n weterer wichtiger Vorteil des revdierten Splex-Algorithmus' gegenüber der Ta
bleauform st, daß er es erleichtert, Datenstrukturen für dünnbesetzte Matrizen zu verwen-
den, also solche m t vielen Null-Elementen. Typischerweise haben die Nebenbedingungsma-
trizen A heutiger LPs nur 1-2 Ncht-Null-Elemente pro Spalte oder Zeile, ggf. mit einigen
Ausnahmen Insgesamt sind wet weniger als 10% der Elemente von Null verscheden. Be
der A k t u a l e r u n g der Tableaus ohne Ausnutzung der Dünnbesetztheit würden viele Re-
chenoeratonen mit Null-Elementen durchgeführt, e Aufwand, der vermieden werden
sollte.
ne wetere Verbesserung bestand n der Enführung der LU-erlegung der Bassmatrix
für ie Lösung der beden Linearen Gleichungssysteme in jeder teration des revidierten
Simlex-Algorithmus' [77]. Ursprünglich verwandte man d e sog. Produktform der Inver
sen [29]. Für dünnbesetzte Matrizen wurde jedoch gezeigt, daß diese zu mehr Nicht-Null-
Elementen führt als e LU-Zerlegung und somit einen höheren Rechenaufwand bedingt
[11]
Berets 195 wurde von .E. Lemke der duale Siplex-Algorthmus angegeben. Heu-
te st er fester Bestandteil aller effizenten Implementierungen, ncht zuletzt weil er ene
wesentlche Grundlage für die Implementerung von Schnittebenenverfahren darstellt.
ine chtge Verbesserung des Simplex-Algorthmus' war sene Erweterung auf LPs,
be denen die Varablen cht nur untere, sondern auch obere Schranken aufweisen können
Außerdem werden für die Varablenschranken auch von Null verschiedene Werte zugelassen
Das Verfahren wurde 1955 von G B . Dantzg selbst aufgestellt und ist als pperboundin
Technik bekannt.
Das P r n g ist ein wchtger Schrtt beim Simlex-Verfahren, der e g e F r e h e t zuläßt.
aher verwundert es ncht, daß sich eine Vielzahl von Verbesserungsvorschlägen um eine
Konkretierung bemühen, die d Iterationszahl des Algorithmus' reduzieren oder sene
Termnaton sicherstellen sollen Be der ersten Kategorie snd insbesondere d e Arbeten
von P.M.J. Harris ] sowie von D. Goldfarb und J.K Rei [52] bzw. J.J. Forest und
D. Goldfarb [47] zu nennen. Sie befassen sich mit Varianten des sog. steepest-edge Pri
cings, für das schon lange bekannt war, daß es zwar zu einer bemerkenswert geringen
terationszahl führt, dafür aber eines hohen Rechenaufwandes bedarf [71]. Harris stellt e
pproximatives Verfahren vor, das wesentlch weniger Operationen bedarf. Goldfarb und
R entwickeln für den primalen Algorithmus Update-Formeln, die den Rechenaufwand
b e m steepest-edge P r i n g mindern In 7] wurden diese auch für den dualen Algorithmus
aufgestellt.
plex-Varanten, d e ene Terminaton des Splex-Algorthmus' zuschern, benutzen
m e t ene Kombination von Verfahren für den Prcing-Schritt und den sog. Quotiententest.
Bedes wird mit dem Begri ivotRegel zusammengefaßt. Erste Ansätze zur garantierten](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-19-320.jpg)
![Einleitung
Termnaton des Splex-Algorthmus' waren e Perturbatonsmethode von Orden und
harnes [24] sowie d e Lexikographische Methode von Dantzig, Orden und Wolfe [30]
Mit der Arbet von Bland 17] begann eine verstärkte Untersuchung von Pivotregeln, d
ne endliche Laufzeit des S l e x - A l g o r i t h m u s ' garantieren. Eine Überscht findet sich
[94] Insgesamt wurde noch n theorescher Ansatz gefunden, der auch in der Praxi
befiedigt. Deshalb werden n heutigen plementierungen Verfahren eingesetzt, die sch
in der Praxs bewährt haben, aber auf ner theoreischen Grundlage basieren 50, 16
Der Quotiententest i auch der Schrtt bei Silex-Algorithmen, der di numersche
S t a b i l ä t des Verfahrens bestmmt. Wenn auch ohne theoretische Stabilitätsanalyse, wur-
de der wesentlche Ansatzunkt zur Gewährleistung der numerischen Stabilität n [60
aufgezeigt. Er st bis heute di Grundlage für robuste Imlementerungen 50, 16]
E n wichtges Arbeitsfeld bei der F o r t e n t k l u n g von Siplex-Algorithmen ist deren
pezalisierung auf LPs t ausgezechneter S t r u t u r . Wichtgstes Beispiel sind Netzwer
probleme, für die der sog. Netzwer-Simplex entwickelt wurde, der von den Datenstru
turen her kaum mehr an Dantzig's Algorithmus ernner [26. E n anderer Spezialfall snd
MultiCommodity-Flow Probleme. Bei desen Problemen zerfällt die Nebenbedngungsma
trix Diagonalblöcke, die durch wenge Z l e n verbunden sind. Herfür wurde von Dantz
und Wolfe eine Dekompostionsmethode entwikelt, bei der iteratv zu jedem Diagonalbloc
ein LP gelöst wrd, um aus diesen Teillösungen ne verbesserte Lösung des Gesamt-LPs zu
konstruieren [ ] . Gerade in der Zeit des Aufkommens von Parallelrechnern, bei denen die
Teilprobleme von verschiedenen Prozessoren berechnet werden können, wurde ies weder
aufgegriffen [74]
Es g b t noch ne Vielzahl weterer Arbeten mi Modikatons- oder Verbesserungs-
vorschlägen zum Simplex-Algorithmus. Den meisten dieser Arbeiten ist jedoch gemein,
daß die evtl. angegebenen Implementierungen nicht alle oben genannten Verbesserungen
enthalten, sondern oft nur auf dem Grundalgorithmus von Dantzig baseren oder sich m
diesem vergleichen (siehe z.B. [25, 37, 82 4]). eshalb bleben diese Ansätze weitgehend
für d e Lösung p r a s c h e r Probleme irrelevant.
Um zur Fortentwklung von Simplex-Algorthmen beizutragen, muß zunächst auf dem
sher geschilderten Stand aufgesetzt werden Dies leiten die in der vorliegenden Ar-
beit entwckelten Implementierungen, und s e treben e Fortenticklung von Simplex-
Algorithmen auf verschieden Ebenen voran
Auf konzeoneller Ebene baseren die plementerungen auf ener neuen arstel-
lung des primalen und dualen mplex-Algorithmus mithilfe einer Zeilenbasis, aus
der die üblche arstellung m t ener Spaltenbasis als Spezalfall folgt. Die gewählte
Darstellung ermöglcht eine einheitliche Formulerung beder Algorithmen für bei
de Arten der Basis und wurde den mplementierungen zugrundegelegt. Desweiteren
wird ene theoretsche Stabiliätsanalyse des Smplex-Verfahrens durchgeführt, und
es werden Methoden der S t a b i e r u n g aufgezegt. Außerdem verwenden die Imple-
menterungen ein Phase 1 LP, das eine größtmöglche Überenstmmung m dem zu
lösenden LP aufweist.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-20-320.jpg)
![Einleitung
Auf Iplementierungsebene kommt ein verbesserter Lösungsalgorthmus für lneare
Glechungssysteme mit extrem dünnbesetzten Matrizen und Vektoren zum Ensatz.
Außerdem wird der Zeitpunkt der erneuten Faktorierung der Bassmatr dyna
misch so festgelegt, daß d e terationsgeschwndket maximiert wird
n software-technscher Hinsicht rd der Splex-Algorthmus enem objetorienter-
ten Entwurf unterzogen Dieser b t e t eine hohe Flexibität und Anpaßbareit, durch
d e es z.B. möglch ist, benutzerdefinierte Pricing- oder uotiententest-Verfahren en-
zusetzen
Als Hardware kommen auch moderne Parallelrechner zum Ensatz. Dies fügt sich
die Tradition der Entwicklung von Simplex-Algorithmen, die stets eng it den jewe
gen Hardwarevoraussetzungen verbunden war. So entwikelte antzg den Simplex-
Algorithmus nur wegen der in Aussicht stehenden V e r f ü g b a r t automatscher Re-
chenmaschinen [32]
Die hier untersuchte Parallelerung setzen an vier Punkten an: Am enfachsten ge-
taltet sich d e Parallelsierung elementarer Operationen der linearen Algebra auf
ünnbesetzten Daten, w die Berechnung des Matrix-ektor-Produktes oder die
Vektorsumme. Dies wurde bereits in anderen Arbeiten erfolgrech durchgeführt [13]
Außerdem kommen in dem Prcing- und Quotiententest-Schrtt parallele Suchalgo-
rithmen zum Einsatz. Ferner werden mit dem BlckPivoting mehrere sequentielle
Iterationen zu einer parallelen zusammengefaßt. Schließlich werden öglichkten
zur parallelen ösung von Glechungssystemen betrachtet. Dabei rd sowohl die
glechzeitge Lösung verschiedener Systeme sowe d e Parallelisierung enes auf der
LU-Zerlegung basierenden Lösers vorgenommen
Es werden drei Implementerungen von r e e r t e n S l e x - A l g o r t h m e n für versche-
dene Hard ware-Archteturen vorgestellt. Sie heßen
Solex für equental bject-orented s l e x
Dolex für strbuted bject-orented s l e x " und
SMlex für hared emory bject-orented s l e x
SoPlex t also ene plementerung für normale s oder W o r t a t o n s mit enem Pro-
zessor. Se enthält alle Konzepte von state-ofthe-art Simplex-Algorithmen nclusive der in
eser Arbeit geleisteten Fortentwicklungen. Wo diese grefen, können Geschwndgkeitsge-
winne gegenüber anderen Imlementerungen e PLEX 27] erzielt werden Damt egne
ch SoPlex für die Benutzung im täglchen Ensatz.
er objektorentierte Entwurf ermöglcht es, alle Egenschaften von SoPlex den ple-
mentierungen DoPlex für Parallelrechner mit verteiltem Speicher und SMoPlex für solche
mit gemeinsamen Speicher zu vererben, nsbesondere seine numerische Stabilität. Für bede
arallele Versionen wurden alle o.g. Parallelierungsansätze imlementert.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-21-320.jpg)

![aptel
idierte i m l e x - A o r e n
n desem Kapitel werden Splex-Algorthmen, genauer r e d i e r t e Splex-Algorthmen,
von der Theorie bis hin zur praktischen Umsetzung beschreben abe werden sowohl
primale als auch duale Algorthmen jewels für zwei verschiedene arstellungen der Basis
behandelt.
unächst wird Abschntt 1.1 die verwendete Notaton engeführt, und es werden
für Smplex-Algorithmen grundlegenden Sätze der Polyedertheorie zusammengestellt.
arauf aufbauend werden n Abschnitt 1.2 Smplex-Algorithmen m t verschiedenen ar-
stellungen der Basis entwikelt. Um zu lauffähgen mplementierungen zu gelangen, müssen
noch wetere Aspkte b e r ü c i c h t g t werden. Zunächst ist dies die numersche Stabilität,
die n Abschnitt 1.3 analysiert ird. Dor werden auch verschedene Ansätze vorgestellt, um
plex-Algorithmen stabl zu machen. Weiterhin muß n geeigneter Start für S l e x -
Algorthmen gefunden werden Dies gescheht mit der Phase 1, die n Abschnitt 1. d i u -
tiert wird. Schließlich bergen Smplex-Algorithmen das Problem, daß sie evtl. nicht termi-
eren. Strategen dagegen werden n Abschnitt 1.5 vorgestellt. Bei sog. Pricng beten
implex-Algorithmen eine große algorithmische Vielfalt; d wichtgsten Strategien dafür
werden n Abschnitt 1.6 vorgestellt. Auch e numerische ösung linearer Gleichungssy-
steme t ein integraler Bestandte jeder plementerung von Simplex-Algorthmen Da
esem Problem eine Bedeutung we über Smplex-Algorithmen hinaus zukommt, wrd es
n einen eigenen Abschitt, nämlich 1.7, behandelt. Schließlch werden in Abschnitt 1.8 ver-
scheden Tips und T r s für eine effiziente und zuverlässige Implementierung beschreben
1.1 tation und themtishe rundlagen
n diesem Abschntt werden wesentlche Begr und Sätze der Polyedertheore zusammen-
gestellt, und es wrd d e Notaton dazu eingeführt. Dies geschieht in enger Anlehnung an
[55], worauf auch für d e Bewese der hier nur zitierten Sätze verwesen wird. Zuvor sei auf
folgende Schreibweisen hingewesen:](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-23-320.jpg)
![KAPITEL 1. REVIDIERTE SIMPLEX-ALGORITHMEN
Di nhetsmatr wird mit / bezeichnet. hre Dimension st allgemenen aus
dem Zusammenhang erschtlich; andernfalls wrd ie durch nen ndex angegeben
Somit bezeichnet In d e rt-dmensionale Einhetsmatrix
ür toren, die nur aus den Werten 1 oder nur aus den Werten 0 bestehen, rd
kurz 1 bzw. 0 geschrieben, wobe Dimension wiederum aus dem Zusammenhang
ersichtlich ist.
Ferner bezeichnet e* den zten E n h e t s v e t o r , wederum der aus dem usammen-
hang vorgegebenen Dimenson
Lineare rogramme nd erungsrobleme der Form
min
1.1
t.
wobe c,x G R , d G Rk und D G R*x seen. Falls es für jedes M G R x GR
gibt, so daß cx < M und Dx > d gilt, so heißt das LP unbeschränkt t hingegen
x G R : Dx > d} = 0, so heißt es unzulässig.
D^ bezechne den i-ten Z l e n v e t o r der Matrx D, Dj entsprechend hren j-ten
altenvetor. Jede Nebenbedngung D^ > dj, mit Z / definert einen Halbraum
n n
i = {x G R : Di.x > di} des R , und d e Hyperebene Gt = x E W : Dix = di} wird
e zugehörige Hyperebene genannt. Lösungsvektoren x von (1.1) müssen alle Nebenbedn-
gungen erfüllen und legen somit im Schnitt aller Halbräume "%, i = , . . . , k. Der Schnitt
von endlch velen Halbräumen st e n Polyeder und wird mi
,d P x G R : D > d} 1.2)
bezechnet. as olyeder , d) heßt das zum 1.1) gehörende Polyeder. Ferner wer-
den später auch Polyeder T , d ) = {x G R : D = d, x > 0} und V{l,D,u = {x G
Rn : l < x < u) benötgt.
ne wichtge Egenschaft von Polyedern st, daß s e ncht nur als Schntt von Halbräum-
en dargestellt werden können. Vielmehr kann jedes Polyeder aus zwe Grundtypen von
Polyedern aufgebaut werden Dies sind für X = x,... xm}
cone x G R : Y7=i Kx» 0} und
conv xtR : Y!t=i ^ >l !}>
wobe xi,..., xm toren und A i , . . . , A kalare bezeichnen, cone X) heßt der von den
Vektoren x^,... ,xm aufgespannte Kgel und conv (X) ihre onvexe Hülle Beide Mengen
nd Polyeder. Für Polyeder P] und P 2 bezeichnet P1P2 = xi+x2 : x G P, x2 G P2}
hre MinkowskiSumme](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-24-320.jpg)






![1.. DI GRUNDALGORITHMEN 15
Entsrechend gelten 1.10 und 1.11, denn durch Ensetzen ' erhält man
cj>(r-e
4>{rD~l - e
T
( r 1 - e c/>(r - e
T
</>(rD--e(r D--eT)
f 9(r - D + <j>{rT - D + < D - ( r - D
( r ( r - D
( r
ie ilesismatri folg iese tz
SATZ 6 (ZEILENBASISTAUSCH
Sei Z = (P, Q) eine Zeilenbasis zum LP (1.1) Seien i e { 1 , . . . , n} und j 6 Q
Dann ist Z' = (P1, Q') mit P = P {Pi} U {j} und Q' Q {j} U {P;} genau
dann eine Zeilenbasis von (11) enn
Dj p])i ± 1.13)
(Z (Z) + @(l,3)-)i 1.14)
{Z (Z) + Si,j) Dp}) und 1.15)
T T
y (Z y {Z) + ^ h j ) D j - ] - e 1.16)
d
i Sj{Z
M) 1.17)
D3.D-])%
VijZ
und i,j) 1.18)
Dip})i
EWEIS:
Bis auf (1.15) folgt alles aus Satz 5, und zwar mit DP_, D = P>p' 9 = i,j),
<f> = $i,j), f = x{Z), f = x{Z% f = dPlg = (Z), g {Z% g = c p = dj, = D3
und l = i. Gleichung 1.15) gilt dann wegen (Z') (Z') {Z) + ®i,j)Dp})j.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-31-320.jpg)





![. D R U H M E 21
BEWEIS:
Terminiert Algorithmus 1 in Schritt dann ist h nach Satz 8 ein optimaler Lösungsvek-
tor von LP 1.1). Wenn Algorithmus in Schritt terminier ist das LP nach Satz
unbeschränkt. Da Agq = AT(A1eq = (AT)q_(AT)E]1ep Afp gilt schließlich nach
den Sätzen 6 und 9, daß in Schritt 6 Z wieder eine zulässige Basis mit dualen Variablen
/ , Schlupfvariablen und Lösungsvektor is so daß die Voraussetzungen für Schritt
wieder erfüllt sind
•
Aufgrund von Gleichung (1.24) hat nach jeder Iteration der neue Lösungsvektor h
höchstens denselben Zielfunktionswert wie h. Für dq ^ gq ist er kleiner, während sons
h = h! gilt, d.h. derselbe Lösungsvektor wird von dem neuen Satz von asishyperebenen
definiert. Solch ein Pivot-Schritt heißt degeneriert. Er ist nur möglich wenn sich beim
Basislösungsvektor mehr als Stützherebenen von V(D, d) schneiden Solch eine cke
heißt primal deeneriert
1.2.1.2 ualer Algorithmus
Gegensatz zum primalen Algorithmus arbeitet der duale auf einer optimalen Basis
h. Gleichung (1.21) ist erfüllt. Sofern die Basis nicht auch zulässig ist, gibt es eine verletzte
ngleichung, etwa q. Sie soll in die Basis aufgenommen werden. Dazu muß eine andere die
asis verlassen und zwar so, daß die neue Basis wieder optimal ist. Anschaulich ist es die
Basisungleichung mit der der neue Lösungsvektor einen minimalen Zielfunktionswert
aufweist (vgl Abb 1.5). Nach den Gleichungen (1.14) und (1.17) uß p also so gewählt
werden daß x(Z') = cTx(Z) + Q(pq)(cDp) und somit Q(p,)-(cTDp^)p = y(Z)pdq —
(Z))/(Dg.Dp^ minimiert wird. Da aber dq > sq(Z), ist dies gleichbedeutend mit der
inimierung von (Z/(DqDp^. Dies wird von folgenden Satz präzisier
SATZ 11 ( U A L E R QUOTIENTENTEST FÜR EINE ZEILENBASIS)
Sei Z = (P, Q) eine optimale Zeilenbasis zum LP (11) q der Index einer
verletzten Ungleichung, also s(Z)q < dq, und t = Dq^,
Gilt 0 so ist das LP (1.1) unzulässi Andernfall ist für
y
argmax ^ > 0,1 < i < n 1.25)
Z = (P', Q'), mit P' = P {p} U und Q{}ö { eine optimale
Zeilenbasis von (11) Ferner ilt
Z^l 1 26)
und
{Z = c(Z) + $ (Z ). 1.27)](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-37-320.jpg)
![22 KAPITEL 1. REVIDIFRTE SIMPLEX-ALGORITHMEN
Abbildung 1.5: Bei einem Schritt des dualen Simplex wird eine verletzte Ungleichung in die Basis
aufgenommen, wofür eine andere die Basis verlassen muß. Die beiden betroffenen Stützhyperebenen sind
gestrichelt dargestellt.
BEWEIS:
Fall 1 (t < 0):
Nach Satz 1 ist x(Z) die einzige Ecke von V(DP., dp). Demnach lassen sich gemäß Satz 3
und 2 alle x G V(DPl dp) als
n
x = x(Z) + ^ V j -Dp]ei
j=i
darstellen, wobei TI, . . . , r n > 0 gilt. Für alle x G V(Dp_, dp) gilt somit Dq,x = Dqx(Z) +
YH=iriDg.Dp}ei < dq + S r = i r ^ ^ dq, d.h. es gibt kein x G V(DR,dP), mit Dqx > dg.
Da also 0 = V(DP., dP) D {x : Dqx > dq} D V(D, d) folgt die Behauptung.
Fall 2 (t £ 0):
Wegen £p = [Dq,Dp^)p > 0 ist nach Satz 6 Z' eine Zeilenbasis mit dualen Variablen
yT(Z') = yT(Z) + $(t T - ej). Da j/(Z) > 0 und tp > 0 ist $ < 0. Für i G { 1 , . . . , n) {p}
gilt yi(Z') = yi(Z) + $*<. Falls ^ < 0 gilt somit j/^Z') > ^ ( Z ) > 0. Andernfalls gilt
wegen (1.25) y{{Z>) = Vi{Z) + $i< > ^ ( Z ) + ( - ^ ( Z ) ) / ^ • tt = 0. Ferner gilt yp(Z') =
yp(Z)—yp(Z)/tp-(tp—l) = yp(Z)/tp = —$ > 0, was die Optimalität von Z' zeigt. Schließlich
gilt nach (1.14) cTx(Z') = cTx(Z) + (dq-sq{Z))/tp-cTDp1ep = cTx(Z)-(sq(Z)-dq)/tp-yp =
cTx(Z) + <S>(sq(Z)-dq).](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-38-320.jpg)

![24 EL 1. R T E S I M P H M E
Anstelle die Vektore g und h in den ritten 4 und u aktualisieren, kann man
sie ebenso neu berechnen (dies wird auch z.B. bei partiellem Pricing in der Praxis durch-
geführt). Die gewählte Darstellung verdeutlicht jedoch besser die Anlichkeit von primalem
und dualem Algorithmus und ist bei vollständigem Pricing auch effizienter [16]. Alle nu-
merischen Berechnungen in den Schritten 2, 4 und 5 treten in beiden Algorithmen in glei
cher Weise auf Lediglich die Auswahl der Indizes p und q wurde vertauscht: Der primale
Algorithmus (in Zeilendarstellung) wählt beim Pricing zunächst einen Vektor, der die Ba
sismatrix verlassen soll, während der duale Algorithmus im Pricing einen Vektor auswählt
der in die Basis eintreten soll. Wir nennen daher Algorithmus auch den entfernenden
und Algorithmus 2 den einfüenden Algorithmus
Wie beim primalen Algorithmus ändert sich auch beim dualen der Zielfunktionswert
des Basislösungsvektors falls der Quotiententest einen von Null verschiedenen Wert liefert
Der Fall $ = 0 tritt auf wenn der neue und alte Lösungsvektor auf gleicher Höhe (in bezug
auf liegen (Z = 0 Solch einen P v o t S c h r i t t nennt man wieder deeneriert
1.2.2 Die Spaltenbasis
In diesem Abschnitt werden sowohl der duale als auch primale Simplex-Algorithmus erneut
vorgestellt, diesmal jedoch mit einer Spaltenbasis. Dies ist die Darstellung, wie man sie
üblicherweise in der Literatur findet. Sie wird hier als Umformulierung eines Spezialfalls
der zeilenweisen Darstellung der Basis vorgestellt
Sofern nichts weiteres gesagt wird, sei in diesem Abschnitt folgendes vorausgesetzt
m, n mit n, j , b Rm und A Rm hat vollen Rang etrachte das
LP
min
1.28)
ieses LP ist offenbar der umgeschriebene) Spezialfall eines LP der Form 1.1), mit
2m + n, = (I und (0, 6 nämlich
min
1.29)
b
b.
Für jede zulässige Zeilenbasis von (1.29) müssen die Ungleichungen {n + 1 , . . . , n + 2m} mit
leichheit erfüllt sein. Da A vollen Rang hat kann man zu jeder zulässigen Basislösung
eine zulässige Zeilenbasis Z (P,Q von (1.29) finden ei der alle Ungleichungen
> b zur asis gehören {ro + 1 , . . . , n + und (Z').](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-40-320.jpg)
![. D R U H M E
SATZ 1
Sei Z = (P,Q) eine zulässige Zeilenbasis von (129) mit Basislösungsvektor
(Z) ann gibt es eine zulässige Zeilenbasis Z (P von (129), mit
(Z (Z und P n + 1 , . . . , n +
BEWEIS:
Sei Z = (P,Q) eine zulsige Basis von 1.29) mit Lösungsvektor x(Z). Setze M {n +
1,.. .,n + m}, R{P) PnM und S(P MR(P), d.h. S(P) bezeichnet die Menge aller
Nichtbasisungleichungen von Ax > b. Gilt |<S(P = 0 so erfüllt Z bereits das Gewünschte
Andernfalls konstruieren wir eine Basis Z' = ( P , Q) mit x(Z') = x(Z), für die S(P)
S(P 1 gilt. Durch |S'(P)|fache Anwendung dieser Konstruktion erhäl n somit eine
sis die d ewünschte eistet
Betrachten wir für ein G S(P den Vektor x = AkD^. Wir wählen ein j G
{ l , . . . , n } , so d ß Pj ^ (P) und Xj ^ 0. Ein solches muß es geben denn sonst hätte
wegen A = ^2PdRrP) XA^ die Matri A nicht vollen Rang N c h Satz 6 ist Z = ( P , Q
mit P' {] U {k} und Q Q {k} U {P eine Zeilenbasis von (1.29) und wegen
sk{Z) = gi $,k) = 0 Somit ist nach (1.14) (Z) (Z' und Z' zuässig Offenbar
git S(P S(P) 1, as den Bewei beendet
•
Diese Satz erlaubt es sich bei de Suche n c h einer optimalen und zuässigen B a s vo
(1.29) auf solche Baen Z = (P, Q) zu bechränken, fü die P D M gilt. Die Zeilen {n +
1 , . . . ,n + m} können somit tet in de Bas verbleiben, w ä r e n d die Ungleichungen {n +
m + 1 , . . . , n + 2 } nie in die Bass gelangen (sie würde sonst ingular) und daher ignorier
werden können. Beides k n n man durch eine angepaßte Verwaltung der Indexvektoren
m d e l l i e e n bei der nur noch Zeilen { l , . . . , n } ausgetauscht weden Um die ffizient
duchfühen u können eignet ich die efinitin einer Saltenbas
EFINITION 5 (SPALTENBASIS)
Ein geordetes Paar S = (B,N) von exvetore B, C { l n }
Saltenbas (zum LP (1.28)) falls folgees glt:
1. Ui { l f j }
2. nN ®
= un
st nicht sinar
Di es a heißn Basisindizes ud d es a Nichtbasindi
Die Zeilenbass Z = (P Q) zu (1.29), mit P N U {n + 1 . n + } h
die zu S gehörende Zeilenbasis Die Vektoren x(S) = x(Z), (S) = s(Z) n
y{S y{Z) heißn der Basslösungsvektor, der Vektor der Schupfvarialen
resve der duale Vektor von S Eine Spaltenbasi S heiß lässig, wnn
T T
(S V b), und ptimal falls c > c x(S) r alle {A b)](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-41-320.jpg)



![. D RU 29
Schritt 5 Up
+Q
+ Q A
+ *(A
Schritt 6: Gee zu S c r i t t 1
ATZ 17 ( P R T I E L L E K E K T H E I T V LGITH
lgorthmu artet artell orre
EWEIS:
Bei Teminierung in Schitt folgt die Behauptung s Satz 15. Wegen Sa t in
chritt 6 B wiede eine as die wegen chitt 3 uch zulässig i t
Für die Unbeschränktheit des LP bei minieung in Schritt 3 betrachte das LP
29) und die u S gehörende Zeienbasi Z (P,Q). Wi identifieren nun die Größen
Agorithmu 3 mit denen a s Sat 9. N c h .33) gilt ]JN{Z) ^ — t(S) und somit
Z) 0. Fener gilt n c h ( fü den Vektor D^} und
A alb i t
Gi also in chitt , so folgt und d m i t n c h Sa die U n b e c h n k t h e i t
de LP
•
Algorithmus a t a t c h eine Umformuieung v n Algorithmus 1 in die N o t i -
n einer Spaltenbasis. Algorihmich e n t r i c h t Algorithmus 3 dem dualen Algorithmus 2:
Bei entsprechender Initialisieung aller reevanten Vektoren und Schranken unterscheidet
ich lediglich das T m i n a t i k i t e r i u m in chitt 1 gemäß de umgekehten Ungeichung
ichtung in (136
1.2.22 ualer Algorithmus
Wie uvor de imale A o r i t h m u w i d nun uch de duale fü eine altenbas umfor
muiet
LGORITHMUS 4 ( U A L E R I M P L E X - L G O R I T H M U S IN SPALTENDARSTELLUNG)
Sei S = B,N) eine opti Zeilenbas on (1.28)](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-45-320.jpg)




















![TEL P L E H M E
lt f o e Zummehä
Is
L
Us
lz Ls
emna gilt für die Zeilebasis < gq < 7 d smit k ie f
Algoritmus 5 verwendet werden. esweiteren gilt g = _/jf > UQ UQ
bzw. g^ = f < LQ = I je ach F l l in Schritt 1 vo Algoritmus 6 omit
eignet sich q = Qz als eintretender I d e x von Algoritmus 5. Wenn wir och
—Agp1 Af zeigen, folgt mit den o e r e n Beziehungen, daß Algorithmus 5 in
Schritt 3 terminiert, da dies auch A l o r i t m u s 6 tut. Nach Satz 26 bedeuted
dies aber die Uzulässikeit des L s u d , da Zeilen- nd Spalten-LP äquivle
s i d , die B e u p t u n g
Es m ß also och A / ) = A% • [Ap] L~ev ^Q1 Ag ezei
werde Wir weisen die d z u ä q u i v l e t e Bezie
(^S (A i8i
ch zu erechn wir ch e e i e t e r ermuttio mit 150)
ÄQ2-nPl 0 Pl
-Tll
1
-nPi J -nP1 -n
-n 182
-n
Ferer ilt für {A~} ch 151
Q2_n q2_n _n _n Q2_n
183
Nu s i d zwei F l l e ZU nterscheide Flls fol -n
es -n mit ist (A
-n —n —n -nQi P , d. 8 wu wie
ll is f T
-n —n wo -n -n
T
' mit ilt T '
-n f Pl -n
Q2—n
-n d Bewe](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-66-320.jpg)
![3 TABITA DE PLEVERF
r Beweis zu all der T e m i n i o in Schritt 3 f r e S p a l t e a s i s basier
der Dualitätsbeziehung zwischen beiden sisdarstellungen und eide Alorithmustyen
Auch der Fall einer Zeilenasis hätte so bewiese werden können azu würde m die
Bedeutung von Zeilen- d Spalten-LP vertauschn, und es müßte n c h der F l l 6 = 9o
ausgeschlossen werden. er direkte Beweis schie da einfacher, zum hnliche Beweise
ereits vorestellt wurde
1. S t a b i t ä t des Siplex-Verfahrens
Die A u f e umerischer Agorithmen ist die Berechnung e i e r Abbildug W1 —• Rm >
Bei der Implementierung auf realen Comutern ist man stets mit dem P r o l e m edlicher
Genauigkeit konfrontiert Da ein Rechner nur ein Gitter von endlich viele ahlenwerte
darstellen kann wird jede reelle Z l durch die nächstliegende Z a l i diesem Gitter appro
ximiert. Also repräsentiert jede im Comuter dargestellte Gleitkommazah ei Intervll und
ist somit a priori f e h l e r f t e t er reltive Feler eutiger 6BitGleitkommaaritmetik
liegt in der Größeord vo ~16
Ein numerischer Algorithmus e s t e t us einer Reihe von R e c h o p e r a t i o e bei de
sich Fehler akkumuliere könne Dies kann so ravierende Ausmaße n n e m e , da as
berechnete Resultat keine v e r n ü f t i e Aussage ü e r die zu lösende A u f b e mehr erlaubt
Auch der Simlex-Algorithmus leibt von diesem Problem ncht verschont. Desha wird
er i diesem chnitt uf sei numerisch chften h untersucht
In de bschnitten 1.3.1 und 1.3.2 werden die Begriffe der Kondition eines numerischen
roblems d der Stabilität eines numerischen Algorithmus e i g e f ü r t . Wir orientiere
ns dabei an den Darstellunge in [34] und 39]. Anschließed wird in schnitt 13.3 die
telle im implex-Algorithmus aufezeigt, die umerische Schwierigkeite sich birgt, un
worauf zu achte ist um eine I s t b i l i t ä t zu umehen. Schließlich werde in Abchnitt 1.3.4
drei verschiede ilisieru vorestellt u d diskutiert die für lex imlementiert
wurde
1.3. Kondition
Ein numerisches Problem r = f(e) esteht dari ei Eingabevektor e £ l ™ uf einen Re
m
sultatvektor 6 E abzubilde. Nun kann der Egabevektor auf keiem Comuter exakt
dargestellt sodern nur durch Gleitkommazahle pproximiert werde. Also reräsentiert
jeder Gleitkommavektor Wirklichkeit e i e U m g E von Eingabevektore, die Feh-
lermenge von e Der o m u t e r ist icht in der Lage, zwisch verschiede Elemente
von zu unterscheide. aher ist es sinnvoll zu studieren wie E durch bildet wird.
ies wird vo dem Beriff der Kondition e i e s Prolems eschrie](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-67-320.jpg)
![TEL P L E H M E
D E I T O N 10 ( K O N D I T O N )
Sei ein numerisches roblem, l e e von und
-x<
f( D ist it der Bezeichnung [X sux,eX ?j für
NI
j§ 18
die Kondition des Problems f. Ist K ~ 1, so nennt ma das roblem ut kon-
ditioniert für K > nent ma es chlecht k o d i t i o i e r t nd für =
nsachgem gestellt
Ferner definiere die K d i t i o eier r e u l r e atrix al
(A -i 8
Die K o i t i o n eines numerisch Prolems hängt somit nicht vo em e w l t e Al
ritmus sodern ist e i e E s c h f t des Problems s e l s t
Wir betrachten die Kondition der Lösung vo linaren G l e i c h s s y s t e m e , d diese
für S i m l e x - A l o r i t m e vo z e t r l e r Bedeutu ist Schritte 2 u
SATZ 28 (KONDITIO E I E R REGULÄREN MATRIX)
Für n G N sei b x, b, Ab M A, Ä, AA RnXn und A ncht singular
derart daß A = A + AA b = b + Ab, und x = x + Ax, sowie Ax = b und
Ax b. Die Größen mit bezeichnen fehlerbehaftete Größen und die Werte A
den Fehler Ferner sei e 4 ^ nd e(A % ^ . Fall (A) < ist
gilt
)) 186
T3ÄÄJ
BEWEIS:
Nach V o r u s s e t z u g gilt AA + d somit = ||A _1 ( +
AAx - AAA) A'1]] • A WA^W • AA • x + WA'1]] • AA • Ax We
A"1!! • lAA|| = ü^- 1 !! • lUll • | | A A | A | | = «(A) (A) < ilt (1 - K{A) e(A))Aa
1
A- !! • lA& + « ) c(A) • x D u s fol
( = | | / | |
1-(A (A |A|| • ||x||
<A
MA ))
1- {A {A
nr n man f r [X] auch e n a Maß wä Ma](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-68-320.jpg)
![3 TABITA DE PLEVERF
tz 28 g t e i e A h ä t z u n g für den ehler des Resultats e{x durc den ler der E
bedaten e(A + e(b). Insbesodere ist für gut konditioierte Matrize mit (A) ~ 1 u
e(A) < 1, die Matrixkondition ) eine gute Approximation für die ditio der ösung
des lineare Gleichungssystems Ax b denn nn ist e( < (A) (e(A) )). D die
ondition K(A) ncht von der rechten Seite b gt, repsentiert sie die Konditio für
lle l i r e Gleichgssysteme mit der Matri d e i e r e l i e e n rechten Seite
1.3.2 Stabilität
Bei der plementierug e i e s Algoritmus zur Lösung e i e s numerischen Problems, wer
den im llemeinen Zwischenresultate berechnet, ei d e e n zusätzliche Feler auftrete
könn Das bedeutet, d ß eine Imlementierung eines Alorithmus nicht e x k t die Abbil
dung / berechnet sodern eine etwas andere Abbildung / . Diese bildet nun e auf f = f(e)
statt uf r f(e a . Wie dieser Feler zu ewerte ist, wird durch die Stabilität e i e s
Aloritmus eschrien
Es ibt zwei A ä t z e zur Behandlu der bilität vo A l g o r i t m e , die Vorwärts
d die Rückwärtsanalyse Wir beschnken uns ier uf den zweite Ansatz, der für die
tabilitätsanlyse der LU-Faktorisierung zur Lösung liearer Gleichussysteme verwendet
wird. ie Grundidee dabei ist, de Feler des Alorithmus / durch einen erweiterten Fehler
der Eigabedate zu modellieren. Dabei repräsentiert e i e Implementierung des Algorith-
mus eine ganze Fmilie F vo b b i l d u n g , mit E F s o s t wäre die lementieru
nicht korrekt
D E F I I T I O N 11 ( S T A B I I T Ä T )
Sei f(e) ein numerisches roblem nd eine Implementierung zur Lösung von
f. etze E = {e : f( f( F} eiß s t i l , falls [ «
und s t i l , falls [E E]
1.3.3 nalyse der Simplex-Algorithme
a bei der Defiitio e i e r B s i s nur azzahli Werte auftrete ist die ndition des ro
blems "Löse ein P mit dem i m l e x - A l o r i t m u s " gerade die Kondition des Gleichung
systems der optimalen, zulässi Basis3. ie numerisch stabile Lösung von dünnbesetzten
l i r e n Gleichungssystemen — und B s i s m t r i z e n s i d tyischerweise d n n e s e t z t wird
chnitt 1 7 se behadelt.
3
Dieses numerische Problem ist nicht äquivalent zu dem Problem "Löse ein LP" etwa mit einem
Innere-Punkte Verfahren Dies liegt daran daß der Simplex-Algorithmus stets noch andere Resultate
liefert, nämlich die Basi und alle damit usammenhängenden Vektoren auch wenn man sich n r den
ngsvektor und den Zielfunktionswert asgeben läßt](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-69-320.jpg)



![1.3. STABILITAT DES SIMPLEX-VERFAHRENS 57
Abbildung 1.6: Stabilisierungen des Quotiententests. Das mathematische Verfahren nach (1.22) würde
die neue Basislösung auf den Kreis positionieren. Aufgrund des geringen Winkels der Stützhyperebenen an
diesem Schnittpunkt ist die zugehörige Basis jedoch schlecht konditioniert. Zur Stabilisierung werden daher
die um einen Betrag ö verschobenen Schranken betrachtet, die gepunktet und mit dunklerer Schraffur dar-
gestellt sind. Die Stabilisierung gemäß Ansatz 1 liefert den mit der Raute gekennzeichneten Schnittpunkt
als neue Basislösung, da in diesem die zugehörige verschobene Schranke als erste erreicht wird. Dieser
Schnittpunkt ist durch das Kreuz gekennzeichnet. Die Ansätze 2 und 3 wählen unter allen Schnittpunkten,
die vor dem Kreuz liegen, den numerisch stabilsten aus. Dieser ist durch das Dreieck markiert.
Dieses Verfahren ist offenbar das "stabilste", das mit der Idee der Toleranz S möglich
ist. Dennoch birgt auch dieses Verfahren dieselben Probleme wie das zuvor beschriebene.
Varianten des Quotiententests von Harris werden z.B. in MPSX und CPLEX eingesetzt
[12, 13].
3. Ansatz (SoPlex Quotiententest)
Es folgt eine Beschreibung des für SoPlex standardmäßig empfohlenen Verfahrens. Wie das
von Harris benötigt es auch zwei Phasen, wovon die zweite Phase mit der von Harris über-
einstimmt. Zur Bestimmung von Qmax wird jedoch erlaubt, daß sich die Schrankenüber-
schreitung um S verschärft. Setze also
c _ j 5 , falls Si > di
%
Si — S sonst.
Damit wird Qmax bestimmt gemäß
„ f di — Si — 5i 1
Qmax = max t — : As» < 0 ^ .
Anschließend wird q gemäß (1.90) bestimmt.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-73-320.jpg)

![DI DE P L E T H
direk agegeben weden kann. A l i e d wird a s d g eine z i g e Bis
für das Ausgangs-LP konstruiert
In Lehrbchern findet man meistens einfache Varianten des P a s e - 1 - L s die zwar eine
numerisch stabile Imlementierung erlauben, jedoch eine hoh Itertionsza edingen. er
einfachste Fall eines h a s e r o b l e m zu (191) ist das L
min
st
(193)
o
0.
Auch hier ist die Basis aus den Varialen s zulässig. Gilt für die optimale Basis-Lösung
von (193) s ^ 0, so ist das Ausgangs-LP unzulässig. Andernfalls ist die optimale Basis
von (193) eine zulässige Basis des zu (191) quivalenten L
min
st
(1
0.
Der Effizienznacteil dieses Verfahrens ist, daß einmal die Basis komplett ausget
werden muß, damit alle "künstlichen" Variablen s aus der Basis entfernt werden.
Das composite Simplex-Verfahren arbeitet deshalb direkt auf den Varialen des
AusgangsLPs und modifiziert das LP dynamisch zur jeweils aktuellen Basis 00]. ei
S = {B,N) eine eliebige Basis von (191) Dann definiert man das zugehörige ase
r o l e m als
min c{BxB
BxB AN
(195
xB
wobei c(B)i = —xBi für xBi < 0 und c(B)i = sonst ist. Dieses Verfahren h t sich ls ef
zient erwiesen und kommt in kommerziellen Imlementierungen zum Einsatz (zB. CPLEX
[16]). Trotzdem erscheint es noch verbesserungsbedürftig, denn dieses hase-1-Problem ist
ausschließlich mit Blic auf das Erreichen der Zulässigkeit konstruiert ercksichtigt aber
nicht die Zielfunktion.
Bei SoPlex wird daher einen andere Strategie verfolgt, die auch in der Phase-1 die Ziel
funktion so gut wie möglich mitberücksichtigt. Außerdem werden wieder keine künstlichen
Varialen dem LP hinzugefügt. Es sei (B,N) eine beliebige Basis von (191) Als
a s e - P r o l e m wird das L
min xB
BxB AN
(196)
xB](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-75-320.jpg)
![TEL IDI PLEITHME
v e r w e n d , wobe k = xBi ür xBi < 0 u d k = 0 s o s t ist ieses LP behält s m i t s v i e
von der truktur des AusgangsLPs bei, wie es die Basis S zuläßt. Außerdem wird die
Schrank / im Laufe der Phase-1 weiter hochgesetzt, sofern es die jeweilige Basis zuläßt
adurch kommt es nicht selten vor, daß ein LP ereits nach der Phase 1 gelöst ist.
Per Konstruktion ist S für das LP (196) zulässig, so daß der primale Simlex gestartet
werden kann. Terminiert er mit einer Optimallösung von (1.96) so ist die optimale Basis
für (1.91) immer noch dual zulässig, und es kann der duale Simplex gestartet werden.
Andernfalls ist mit (1.96) auch das Ausgangs-LP unbeschränkt. Entsprechend kann auch
ein Pse-1-Problem durch Manipulation der Zielfunktion konstruiert werden, für das die
asis 5 dual zulässig ist. n diesem Fall wird zunchst der duale implex verwendet
Eine Implementierung für allgemeine Basen gemäß Abschnitt 1.2 gestaltet sich be
sonders einfach. Es muß lediglich eine andere Initialisierung der S c h n k e n erfolgen und
zwischen eiden Algorithmustyen umgeschaltet werden.
1.5 reiseln u n d dessen V e r m e i d u n
Wenn der primale oder duale Algorithmus eine unendliche Folge degenerierter Pivot
Schritte durchführt, spricht man vom Kreiseln. Das ist die einzige öglichkeit dafür, daß
ein SimplexAlgorithmus nicht terminiert. ies sieht man wie folgt: Es gibt maximal Q)
verschiedene Basen zum LP (1.1). Bei jedem nicht degenerierten PivotSchritt ändert sich
der Zielfunktionswert des Basislösungsvektors streng monoton fallend für den primalen
und streng monoton steigend für den dualen Algorithmus emnach kann die alte Basis
nie wieder angenommen werden, so daß maximal ^) — 1 nicht degenerierte PivotSchritte
öglich sind. amit ist folgender Satz bewiesen
SATZ 30
ei Simpex-Algorithmus ht termiiert, kreiselt er
ie Vermeidung des Kreiseins ist somit eine wichtige Anforderung für die Brauchbarkeit
von Simplex-Algorithmen. In [26] wird das Kreiseln zwar als ein rares Phänomen beschrie
ben, das in den meisten Implementierungen aufgrund numerischer Feler nicht auftrete und
somit nicht berücksichtigt zu werden brauche Heute werden Simplex-Algorithmen jedoch
vielfach für kombinatorische Optimierungsroleme eingesetzt, ei denen die Nebenedin
gungsmatrix oft nur aus Werten 0, 1 und besteht und das LP sowohl primal als auch
dual degeneriert ist Die dabei auftretenden Basismatrizen sind häufig so gut konditioniert
daß die egeneriertheit auch numerisch erhalten l e i t Desalb kann das Kreiselrolem
nicht m e r unercksichtigt leiben.
Es gibt eine R e i e theoretischer Ansätze [17, 99, 9 103], die ü e r pezielle Pricing und
Quotiententest verfahren ein Kreiseln ausschließen. In praktischen Implementierungen wer-
den sie jedoch kaum eingesetzt. Ein Grund dafür ist daß eine strikte Verwendung solcher](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-76-320.jpg)
![1.5. KREISELN U DESSE VERMEIDU
Pivot-Verfaren in de Regel zu wesentlich mehr Iteratioen führt. Dies kann z B . d d u r c
umangen werden, daß, solange ein Fortschritt bei der Lösung erzielt wird, eine besse
re Pivo-Strategie verwendet und erst, wenn mehrere degenerierte Schritte nacheinander
a u s g e f r t worden sind, zeitweise auf eine Kreiselvermeidungsstrtegie umgeschaltet wird
Ein anderer Grund, theoretische Kreiselvermeidungsverfaren nicht in praktischen Im
plementierungen einzuseztzen, ist, daß sie bei numerisch stabilen Implementierung nich
mehr anwendbar sind. Sie basieren meist daauf, daß die Basislösung während des Krei
seins unverändert bleibt Wie in Abschnitt 1.3 beschrieben wurde, trifft diese Voraussetzung
bei numerisch stabilen Implementierungen auch im degenerierten Fall nicht immer zu, da
eine leichte nzulässigkeit toleriert wird. Dadurch ist es möglich, daß ein "numerisches
Kreiseln" mit leicht variierenden Lösungsvektoren und schwankendem Zielfunktionswert
entsteht. Z.B. kann bei Algorithmus 1 eine Verschlechterung des Zielfunktionswertes auf
treten, wenn eine Variable di — 5 < Si < di die Basis verläßt. Dies kann durch sog Shifting
verindert werden, ei dem die Schrank di z.B. auf s erasetzt wird.
as Shifting bildet die Grundlage für die Kreiselvermeidung von SoPlex, die nun anhand
von Algoritmus 1 eschrieben werden soll. Sie ähnelt der in [12] vorgeschlagenen M e t o d e
die bei MPSX zum Einsatz kam. Nach maxcycle Pivot-Schrtten ohne Fotschritt
beim nächsten PivotSchritt enen Fotschritt ezwungen, ndem fü alle i, mit s* di + 5
und Asi < 0, d e Schranke di auf di « s and(1005, 10005) gesiftet wid. i ist
nd(1005, 10005) ein zufälli aus de Intevall (100,10005) gewälter Wert. Für den
aameter maxcycle hat sch We n de rößenodung 1 e w h r (vgl A c h t t
2.8).
er Zwek de zufälligen W a l von di ist, d e e g e n e e t auch zukünftige
PivotSchrtte aufzubechen. Andee Verfhren p e t u e n deshalb das gesamte LP, even
tuell soga gleich zu Beginn. ies eschent jedoch e ungünstig, da so meist m h r
SimplexIteationen notwendig weden als ohne P t u b a t o n : Oft at man nämlich Gl
und der SimplexAlgorithmus v e ä ß t ene degeneriete cke o n e weiteres Zutun. Beim
g e s t t e n LP ist eine solche Ecke n eine Sch von Eken aufgebrochen, die der Simplex
Algoithmus nun einzeln travesieen muß. Entsprechend eicht es völli aus, wenn de
SimlexAlgoithmus eie optimale Basis findet im g e s t t e n Fall st des zwangsläufig
auch e enzge und somit schwe zu finden.
Handelt es sich m e P h a s e 1 b l e , so ist das Shiften des LPs u n p r o l e m a t c h
handelt es sch doch n e n schon um ein LP mit v e ä n d e t e n Schranken. Andefalls muß
nach T e m i n i u n g mit de jeweils dualen Algoritmus fotgefahren weden. es w d so
lange t e t s e n A l g o m u s au de unverändeten L t e m i n i t .
Es g b t keinen Terminationsbeweis fü ine solche Kreiselvemeidungsstatege. In de
P x i s sind jedoch noch kene Fälle aufgeteten, denen de A l g o t m u s ad nfintum
zwschen den asen u s c h a l t e t , wel das LP imm weder verändet wude. es kann
dadurch wete chwet weden, ndem man d e Anza maxcycle d e g e n e t e Pivot](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-77-320.jpg)
![62 TEL 1. REIDIER PLEORITHME
Schrtte vo de Stufte jede chalte chsetzt.
Ein weiter Vorteil von Kreiselvereidungsstategen mittels Shifng gegen dem
Umschalten auf theoretisch S t a t e g e n st, daß d gewählte ing-Strateg beibehalten
weden kann. Außede d en s t k e odulater Seentwu öglcht.
N e e n den Arbiten zu eoetischen Kreiselvermeidung g b t es kau Liteatur übe
p r a k t a b l e Strategien. I b e s c h r e n Gll Murray, Sauders und W r g t eine Strate
e, bei der de T o l e r a n z a r a e t e r 5 beim Harrs-Quotiententest mi jedem PivotSchrtt
hochgesetzt w d . Wenn anscheßend in de zweten ase des Quotententests kein Fort
schritt e i e l t wid, siften s e die Schranke um den aktuellen , und da 5 öße st
als n de vorigen I t e a t o n , w d so e n Fotschrtt ezwungen.
Zwei Nachtele sind b i diesem Vefahren gegen dem zuvor beschrbenen zu ver
zechnen. Zum enen wchst de Toleanzparamete S mit jede Iteation. es entsprcht
ab einer glechzeitigen R e l a r u n g aer Schranken, auch wenn des icht notwendg wäre.
nsbesondee st nach T e m i u n g d e Lösung bis auf das geade aktuelle zulässig, und
n aller Regel muß ene w e t e e P a s e angeschlossen werden. Zum anderen hren degene
rierte Pivot-Schritte a. w e t e e V a b l e n n die um 5 relaxierte Schranke heran. Dadurch
schränkt man die W a l f r e i e i t b i m n u m e c h e n Quotententest wiede unnötig ein. Ins
besondee ist die Erhöhung von essentiell fü ine numerisch stabile Impleentierung. I
57] wird scheßlich eine Gegeneispiel angegeben, das diese K r e i s e l v e r d u n g nch
funktioniert. Di Konstukton eines solchen Gegenbispiels s c h t e t jedoch r r n d o m i
te Ansätze w e s r S l e x zugundegelegt wuden.
1.6 ricg-Straten
Be de Aufstellung der S i m l e A l g o i m e n wude im jeweiligen Pricing-Schritt ledg-
ch e Bedingung fü w ä b a r e ndizes genannt. S m i t snd vele Varianten von Algoith-
en öglch, die sch in der konketen Auswal, der sog. Pricng-Strategie, unterscheiden.
i ist geade sie von entschidende Bedeutung ür die Anzahl von Iteratonen und
somi für di Effizenz von i m p l e x A l g o r e n . Es ist jedoch keine Strateg ekannt
für alle L P P o l e e a ffizentesten a t e t . eshal weden nun ene e von
ng-Srategen vogestellt.
Der nfchheit h a l e r gehen w dazu au das L 1.1 und die Algorithmen 1 und
zurück. Die Eweiterung au e A l g o e n mit allgemener Basisdastellung ist prblem
los öglich, fordet jedoch ine k o t e e Notaton e d e zugundelegenden deen
nu v e c h l e n w r d e .](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-78-320.jpg)


![1.6. R I C T E G I E N
Abbildung 1.7: Das steepest-edge-Pricing rhindert, daß aufgrund unterschiedlicher Normierungen de
Richtungsvektoren A#W eine weniger steile Richtung gewählt wird. Diese Situation ist in der Abbildung
dargestellt. Obwohl Ax^ einen geringeren inkel zum Zielfunktionsvektor —c aufweist als AxW s m c i di e
zugehörigen reduzierten Kosten höher
e B e c h u g de erte pi ach (1.97) e d e t e e i n h h e R e c h n a w a d .
jeden W r t müßte ein l i a r e s Glechungssystem zur Bestimmng n AxW gelöst un
darüberhnaus ein Skaarprodut b c h n e t weden. Aus dese Grund galt d s steepest
edge P n g ang Zet als zu aufwendg obwol bekannt war daß es zu e e rheblche
Redu de ahl der votSchritte fhren kann st als Goldfarb u Red U p a t e
Foel die Göße pi m u l t e n , wude es zu e rakkable V e f a h r n [ 7]
Es weden nu die UpdateFomel pi f de i m l e n Simplex in Z l e d a r s t e l l u n g
aufgestellt. Dese Darstellung ubt e essees e o e t c h e s Vestän ls de n [2]
beschrttee W
ei Z Q) d ass nach e i m Pvot-Schrtt mi Indzes p u d q. Nach (1.1
st die neue B p = VP
> mit V = I epqD^1 — £) u nach (1.89) lt
V-1 = I e
*u p x^ Z ann glt mi 'x® ^
T
= p}:
1
'j( ~ -
-]fß
x® f • x^ i
p] e ££ f x^ sost.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-81-320.jpg)

![1.6. RICTEGIEN
1.6. rici
Beim Devex cing handelt es sich u eine Appoximat des steepest-ede P r n g
be de ei ichst inge Rechnaufwand anällt, indem Multplkato pi ch
exakt bestimm w e d e . Es wude P. Harr rgeschag ]
ü de e f ü g d e A l m u s anstelle 1.1 f o l d e Upate
Foel wedet5
fH + ( ! £ ) W 1-1
ür i q kann weite 1.12) w e d e t weden. Man erhält (1.13) durch enfaches W g -
sse des Smmanden n (1.101 de ösung des zusätzlche G l e c h n g s s y s t e s u
e B e c h n u n g der Skalarpodute e o d e r n wüde. E n t s p c h d e r h l t an de
r n d e n Simplex r i ^ p d e U p t e F o e l
Pi + (j 1-1
wobi f r i = ede 1.99 w e d e t wid.
Die U p d t e F o e l n des Devex P r i n g s führ zu ß die Gewichte pi stetig an-
wachsen. m dieses Wachstum zu begrenzen, wede sie auf 1 zuckgesetzt, sobald e
Gewcht e n Schwellwe ü b e c h r t e t . Es hat sch n Schwellwe 06 bewährt.
1.6.7 igh ricin
W e das steepestede ode Devex Picing utzt a c h da weighted P c i n g r ä f e r z p a -
r a e t e pi fü e PivotAuswah m G e g s a t z zu de erstgnannten werde iese s t c h
beim art des i m p l e x A l g m u s festgesetzt u ncht b jeder SimplexItera ak-
t u l i s t . olch Verfahren eignet sich, wenn man über ne gute H e u s t i k v e r g
die I n f m a o e zu lieern kann, welche Bedingnge bei de optimlen Lösung mi
Gleichht efüllt se wird. Es ö n n n ber a c h Gewchte r allgeeine Ps onstuie
weden, e des Abschntt 1.8. ch Kost r S a r t b s beschrebe
d.
arris spglic
i = j , [^-zM q
vorgeschlagen. Diese Approximation e r s c i n je als (11 sic st
mit SoPlex als die schlechtere erwiesen.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-83-320.jpg)

![17. LÖSU LINEARER GLEICHUNGSSYSTEME MIT DER BASISMATRIX 69
R e p r ä s t a t i o n d r N N s e i n r M i x ab. eute f g t e l l t e LPs s f a t imme nn
etzt nabängig von der R e c h c h i t e t u r
Es g t zwei Anätze zur u m e c h e n ösung von linearn Gleichungssystemen n i c h
direkte u d iterativ ö . Wie i Abschitt 7 aufgezeit wird, rscheien letzte
den rste Blick vieverspreched scheiden jedoch aus da ihre Konvergen nicht g n ü g n d
abgsichert werden kann. Dehalb werden bei Impemetierung des Simpex-Algorithmus
direkte M e t h d e eingeetzt. ie werden in den A b c h i t t e n 1 . 2 und 17. diskutiet. In
letzteem wird auch die für SoPlex impementierte ersion ein LU-erlegung de Ba-
ix beschiebn. In A b c h i t t 17.4 w i d die Lsung von Gleichngssystemen ei
ggebene L U - e r l g u n g de ix b e c h i e b n . Aus Effiziengrnde t e angezeigt
eine L U - Z r l e n g der B s i s i x für ein lge von P i v o t c h i t t e tzen. Zwei
Methden, die t n , wede chitt 5 votell
1.7 rative Lös
Itertive Löse für l e a r e eichungssysteme bess i t e t i v (daher der N m e eine
Approximation de ö s u n g s v r s bis die ewünschte Gnauigkeit erreicht wird. In jede
I t e t i o n geht meist ur die Matrix der Vektor der rechten eite d die ktulle Appr
ximtion de Lösungsvektrs ein, wdurch der Speicheed im G a t z z d i k t e
L n für d n n b e t z t e M a i z e n b c h ä n k t bleib
ür die Impementierung von implex-Agorithmen erscheint ein weiteer P u n t vor-
teihaft. G i t es etwa beim duaen Simplex noch „ehr sark" vrletzte Ungeichungen,
erknnt man diee uch wenn die Genaukeit des k t u l l n B s l ö s u n g k t o r s noch
ng ist. Mit Fotschreiten der Lösung des LPs kann die G n a k e i t der L ö s u n g s k
n angepaßt werden. Dabei kann de Lösungsvektor der vor implex-Iteration ls
t w e t für die i t e t i v e Lösung de Geichngssystems für den neu asslsungsk
to tzt weden. iete iteative L e ssere Ansätze zur llelierung als
die wärts- u d rtssubstittion, da ihnen w e n i r Sequetialität i h ä n t ist
[83 8, 66]. G r u d genu also, die A n w e b a r k e i t i t e t i e r Geichungssystemsl für
den impex-Agoithmus u untersuchen. Dazu be w r ein kurze E i n f r u n g die
M t e i e ür ei fassde blick sei z a f [ 4 6] wien.
E gibt zwei Anätze für iteativ eichngssystem Klssche tetionfa
b a i e n af e i r Fixpktitetion
xfc = Gxk + gmit ~lB ~lb (110
wobei Q~l ein (regulär Appoximation von B~l ist. Offenba nach Konv x
1
Xfc Xk die Lösung des Gleichngssystem denn aus x = Gx + g = ~ (B folg
Bx = b. Verschiedene I t e r a t i o n s v f a e n nterscheide ich in der W von Q chon
beim einfache F l l symmetrche positiv d e i t e r M i z e n B k o n v r g i e n d e r t i g e
tetionfa j e d c h nur falls der S p e k t l r d i u s mit cheide ie](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-85-320.jpg)
![KATEL 1. REIERTE MPLEX-ALGORITHMEN
für die A n w e g n SimplexAlgoithme us d e n für l l m e e B i z
kei Konv g a a n t i e t weden. 7
Modeere teationsfahr nd Varianten des V f a n s der konjgierten G d i e
ten. Ihr V t e i l i t , aß für b e l i e g e s y m m e t c h p o i t i definite Matize die Konvrgen
nachgewie weden kann. Die o n v c h w i d i k e i t hängt j e d c h von der Kondi
tion de ix B ab
xk xk)< ^3ß X o x 0 ) (110
lJ
Erweiterungen von Konugierte-Gdienten-Methoden a s y m m e t c h e M i z e n ba
i e n a der S y m m e t i e r u n g de Gleichngssystem
= B (110
Die rschechtet j e d c h die K o n v g c h w i d i k e i t , denn
E n e erbessrung der Konvegenzgeschwindikeit von K o n i e t e n - G r a d i e n t e M e
t h d e n beteht in der sog. Vorkonditionierung. D w i d die M r i x B von beiden Sei
ten mit e i r Vorkonditionierungsmatrix C zw ultiplizie Die Matrix C w i d s
ewählt, d ß mit ih die Geichungssysteme direkt ösbar s , und die Kondition von
BCT klein t Für Gleichungssysteme die aufgrud i h r r Hrkunft (etw der Lösung
partieller Dierentialgleichungn) eine vohersagbare Struktur a b n , önn wirkung
volle poblempezifische rkonditionie n t w i c t weden.
Für den satz in e i e m llgemeinen Simpex-Agoithmus bed es jedoch eines
rläßlichen allemeingültig orkonditioniers Die ntsäche r einer Approxi
mation ei dirkte L ö r s amit llte de axi ew ein vollständi
dite de ten.
Auch wenn iterative Löse für Simpex-Algoithmen ausscheiden, könnten sie den-
noch für die Lineare Pogammierung von Nutzen sein. Der H a p t f w a n d innre-Punkte
V f a h e n beteht i de ösung von Gleichngssystemen mit de M i x ATA, wobei A die
N e b e n b e d i n g u n g t i x ezeichet Diee ist nbar symmetrisch und e bleibt zu unte
suchen, ob damit nügend Sruktur vorhanden i m ein geeigneten Vorkonditionierer
d e f i i e n . Ein mögicher Vorteil bei de Anwendung iteratier öser läge i de sse
n P l l e l i s i e b a r k e i t und in der öglichkeit, inexate Methoen zu r e s i e n , d die
G n a u k e i t de Lösung von Gleichngssysteme de k t l l fodess i n n l
de n n P t e f a a n s s n .
7
Es gibt sogar eine Publikation [37], die eine Implementierung des Simplex-Algorithmus mit dem Gauß
Seidel-Verfahrens (Q ist die obere Dreiecksmatrix von B) beschreibt Allerdings ist diese Implementierung
eher ein Kuriosum als ein zuverlässiger Algorithmus](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-86-320.jpg)
![17. LÖSUNG LINEARER GLEICHUNGSSYSTEME MIT DER BASISMATRIX
1.7.2 Diekte Metoden
Bei d i t e n Lösungsvrfahn wird die M i x ein P r u k t von Matizen trans-
formiert, mit denen Geichungssysteme dire st wede können. Beim Simpex-
gorithmen k m m e n ei zwei Typen von Mtrizen zum Einatz, Rang-1Updte
M r i z e und Deiecksmtrizen. Andee d i t e Lösungmethden, wie z.B mit Gi
R o t i o n n ode HousehdeReflexionen [4] werden trotz bssere m e r c h e Egen
schaften fgrund ihres ö h e n R e c h e n a a n d s u d der schechte A u s t z n g de
B e e t z n g r u k u r icht wedet
RangUpdteMize ab die
T
ei(ri (110
u d wurden b e i t s für de B a s u s c h (vgl. (1 e i n g e h r t . Die Invrse solcher tri
zen kann nach (189) d i r e t anggeben werden, aß sie ich zur Kontruktion diekte
sungfa e i g n . Die ksseitige Multipikation e i e r Matrix B mit V e r g i t die
Matrix = B ei(rT die us urch A u s u s c h der lten Zeie mit j1B
sultie
H i s r i s c h wurde für den idiete Simplex-Agoithmus z c h s t die og. Produkt
fom der Invrsen (PFI) erwendet 5 63] Bei de PF w i d die h e i t a t i x durch d
a x i m l nfache P u k von R a n g U p d a t e M i z e i die M i x anfomiet
Vn
Stimmen ei e i g e Zeilen von B mit de Einheitmatix überein, so bedar ntspe-
chend wen Matrixmultiplikationn. Die eihenfoge der u s e t u s c h t e n Zeile t dabei
tcheide für die m e c h e bilitä d de p e i c h e c h de P I
Beim Simplex-Algoithmus werde die Vektoren r/ ohnehin für die Update echnet
o daß die PFI als die für Simplex-Algoithmen naürliche Wahl r s c h e i . Im fe de
Simplex-Algoithmus immt j e d c h die numeische Stabilität der I ab und de enöti
te S p e i c h e r a a n d zu Deshalb m ß die P I von eit z Zeit mit ei ss
Pivoteihenfog e c h e t weden.
Untersuchunge aben gezei aß die PFI a. e i n öß Speicherbedf afweist
ls die im nächsten Abschitt dargestellte LU-Zerlegung 11 a der Speicheredaf et
wa der Berechungzeit zur Lösung von Gleichungssysteme enspicht, v w e n d e n heutig
mplementierung des Simpex-Algorithmus die L U - e r l e g n g de B a m t r i x Dennoch
blei ch die PF weitehin inteessant denn R a n g U p d t e M i z e wede m i t n t e
für uschchitte w e d e t vg b c h i t t 5)](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-87-320.jpg)


![KATEL 1. REIERTE MPLEALGITHME
obei e die Maschinenauigkeit eichnet 39] Somit muß da c h m de Maix
emente wähend de l i m i n a t i z e s s s k n t l l i e t weden
Bei der Pivot-Auswah ietet ich eine Mglichkeit das Wachstum de K o z i e n t e n
während des iminationspozesses zu teuern. Offenbar f ü e n kleine Werte ^ in
Schritt 3 ehe zu einem Anstieg der Koeffizienten als groß. erschieden stab ian-
ten des LU-Zerlegungsalgoithmus unterscheiden ich dahe dain, mit welchem Aufwand
nach betagsgroßen Pivot-Eementen gesucht w i . Beste S t a i t ä t bietet natürlich die
og. vollsändige PivotSuche, bei der jeweils das betragsgrößte Element der ativen Ma
rix BfsJ gewählt w i . Dessen Betimmu bedeutet ab ft einen nicht azeptablen
Rechenafwand, daß meist weniger s t e n Vaianten z Einsatz kommen. Oft wird
da betragsgrößte Element einer Spalte ode Zeil gewäht (partielle PivotSuche). Wie
im folgenden Abchnitt eschieben weden ei d n n etzten Matizen ch weni
ene Anfoderuen tell
1.7.3.2 Pivot-Auswahl für dünnbesetzte Matrizen
Während eine iminatinsschittes kann in Schitt 5 ein lemente B? +1 werden
für das Bf 0 g a t Derati Elemente heißen Fülelemente Damit auch die Faktoren L
und U d ü n n e t z t l e i e n da eachtet weden da öglicht wenig Fülemente
enttehen
Das folgende i t das Standardeispiel für den entscheidenden Einflß der Pivot-Auswah
die A n z h l vo Fillementen ä h t man bei einer Matix mit de B e e t z g s s t r u k t u r
V
als Pivot-Eement •, o entsteht nach diesem Eliminatinsschritt eine dicht setzte Matrix
Wählt man hingegen ein andere Diagonalelement, so entteht kein weiteres Fillelement
Leider ist die B e t i m m g der Folg von Pivot-ementen die zur g i n g s t e n Menge vo
Fillelementen f ü , ein P-schwer oblem [10] D e h a b urden rschiedene Heuri
tiken entwic m den F l l g i n haten.
s g b t zwei grundlegende Ansätze zur Fillminimierun Der eine steht darin, die
Matrix worder Ftorisierung so z permutieren daß anschließend die Diagonalemente als
Pivot-emente verwendet werden können und möglichst wenig Fülelemente aftreten Ein
Beispie hiefür sind s Skyline Slve bei denen eine Permtation de Zeilen und Spaten
de Matrix esucht wi daß lle NNEs „nahe" an der Diagonalen liegen. Dadurch i t bei
der anschlieenden F a t o r i s i e r u g gewährleistet daß sich der Fill uf einen engen Beeich
um die Diagonale (die Skyline) beschänkt. Diee M e t h d e e i n e t sich b e n d e r s für den
symmetischen F l l , wenn zustzlich noch eine peziell Struktur de M a i x usgentzt
weden kann (etw vo F i n i t e e m e n t e G i t t e n )](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-90-320.jpg)
![17. LÖSUNG LINEARER GLEICHUNGSSYSTEME MIT DER BASISMATRIX
Der zweite Ansatz ist die lokale Fllminimierung. Dabei weden während des liminati
nsvorgan die Pivot-Elemente gewählt, daß in jedem Schitt nur ein geringer Fill z
waten is Für M a i z e n hne bekannte Strukur haben sich kale Methoden als ü n t i
ge wiesen. Seien rf nd cj die Anzahl der NNEs in der i-ten eil bzw de j-ten pate
de aktiven Matrix BaJa im s-ten Eiminationsschitt Dann ist m|- (r| )(c^ —
ween Schritt 4 eine o b r Schrank für die Anzah vo Fillelementen die ei de Wahl vo
Bf ls P i v o t e m e n t im s-ten Schitt entstehen kann Man nennt m?„ die MarkowtzZahl
de Eementes B Lokale Pivottrategien wählen als PivotElemente s c h e mit ringe
Markowitzahl. Verschiedene ianten unterscheiden sich darin, wieie Afwand für die
Suche nach ementen mit n i e d g MarkowitzZhl getieben w i d
Bei der Fillminimierug muß j e d c h auch die Stabilität der LU-Zerlegug berksichtig
werden Wie in 17.3. beschrieben müssen dafür Pivot-Elemente mit möglich großem
B e t r g gewählt werden. Es g t also, einen Kompromiss zwischen Fillminimierung (kleinste
MarkowitzZahl) und Stabilität betragsgrößtes NNE) zu schließen. In der P a x i ha ich
dafür die Schwellwertpivotsuche bewährt ür einen v o r g e n e n Schwellwe 0 < u
weden als PivotElemente ll NN r l b t , für die
> ma 11
gil ür u = 1 entspicht dies der partiellen PivotSuche K e i n e e Werte von u r l a e n
die Wahl von P i v o t e m e n t e n mit kleinere Markowitz-Zah glicherweie j e d c h
Koten der S t a b i t Als ti h a e n ich Schwellwete 01 wieen
1.7.3.3 Implementierung
In den v o e n beiden Abschnitten wurde de Rahmen für die Wah des sugsvefahren
für line Geichungssysteme im Simplex-Algoithmus bgestect. Nun oll die für So-
Plex g e w ä t e Vaiante nd deren mpementierung vorgestellt weden. Dabei git es zwei
A s p e t e z b c h e i b e n , in denen ich Unterschiede verschiedener m p l e n t i e r u e n vo
LU-Zrlegungsalgorithmen für dünnbesetzte nicht symmetrische Matizen m a n i t i e r e n
Die ist z m einen das zugrundeieende Datenlayout zur Speicherung der dünnbesetzten
Marizen und zum anderen die S t r t e i e bei der Suche nach ü t i e n P i v o t e m e n t e n
im inne der Schwellwetpivotsuche
E gib eine Reihe unterschiedicher Speicherschemata für n n e t z e Matrizen
39, 89]. D a e i nterscheidet man zwichen der Speicheru der NN in Feldern nd ihrer
peicherung in verketteten Listen Von der Komplexitätabschätzng her sind für LU-
Zerlegugsalgoithmen, bei der F l i e m e n t e entstehen nd ander Eemente Null weden
können, doppe verkettete Liten b o n d e r s geeinet [89]. Auf heutien Cachechitekt
en t e t e n ab ei einem L i t e n a n t z häufig s CacheMisss 9 f da kein gul
Ein Cache-Miss führt dazu, daß der Prozessor seine Arbeit einige Taktzyklen unterbrechen muß
bis die geforderten Daten vom Hauptseicher nachgeladen w r d e n . D a d r c h verlangsamt sich di
earbeitngsgeschwindigkeit](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-91-320.jpg)
![KATEL 1. REIERTE MPLEALGITHME
HstartDL] HStartEj]
Feld
num[i]
max[i]
Abbildung 1.8: Speicherlayout für di NNEs der Zeilen der Arbeitsmatrix beim LU
Zerlegungsalgorithmus von SoPlex: Alle NNEs aller Zeilen werden in einem gemeinsamen NNE-Feld
gehalten. ür die ite Zeile wird jeweils ein Zeiger s t a r t [ i ] a f das erste NNE in dem Feld sowi di
Anzahl num[i] der NNEs der i-ten Zeile geseichert chließlich wird di Anzahl der NNE i Feld bi
r nächsten Zeil in max [ i ] verwaltet
peicheug lg
D e h a b urde für SoPlex einer Speicherung in Feldern der Vrzug ggeben, ähnich de
in 92] bschriebenen. Die A e i t m a t i x w i d zeienweise a b p e i c h e r t : Die NN all
Zeilen weden in einem Fel ltet. Für Zeile i w i d in s t a r t [i] ein Zeiger da
erste NN in dieem in num [i] die Anzahl der NNE des Zeilenektrs und in max [i]
die Anza de im f ü g b e n NNESpeichelätze i ur ächten Zeil peiche
(gl Abbd 8
s weden als nicht nur die NNEs sndern auch die cher dazwischen vewaltet: Die
D i r e n z max [i] - num [i] b c h r e i b t unbenutzten NNE-Speicher, in dem Fillemente für
die te eile erzeugt weden können. Entstehen hingeen Fllelemente wenn max[i] ==
num[i] w i d die betffene Zeile an da Ende de benutzten Teils des NNEFldes
kopiert w ch genügend peicherplatz für die Fill-Elemente breitsteht (andernfalls
w i d das Fed rgrößrt). Dabei wird der von de verschobenen Zeile z v o b e a n r u c h t e
Platz de davor efindichen Zeile als freier N N E p e i c h e hinzugefügt. Um dies effizient
durchfüren zu können, werden all eien in eine d p p e l rketteten L i t e watet die
nach de Anfangsaddsse im NN tiet i
chließlich weden die Indizes de Matrix-NNEs auch paltenweise a e s p e i c h e t , wobei
dasselbe L a y o t benutzt w i d Dies glicht a c h einen patenweien u g r f minde
die Indize der NNE de M a i x
Das zweite Unterscheidungskriterium für vrschiedene L U - F i e r u g s l g o r i t h m e n
ist die Pivot-Ausah A c h hie ientiert sich SoPlex an der in 92] chriebenen Stra
t e i e , die wiederu gerinfügi geändet wurde. E werden d p p e l t verkettete Listen
Zi und St für i = l . . n g e r t . Jede Zeilenindex i und Spaltenindex j der aktiven
T e i m a i x wird in der Liste Zr bzw Sc* verwaltet. Wenn ich die Anzahlen der NNEs r
oder ei einem PivotSchitt ände weden die Indize bzw j in die e n t e c h e n d e n
Liten rschoben](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-92-320.jpg)
![17. LÖSUNG LINEARER GLEICHUNGSSYSTEME MIT DER BASISMATRIX
Die Liten ermglichen einen schnellen Zugrf a f Zeien bzw Spaten mit enau i
N N E . Insbesonde kann schnell von kleinen W t e n auwä die Zeile oder Spalte mit
der g i n g s t e n Anzahl von NNEs sucht weden Aus einigen (1-4) in diesem Sinne ersten
Zeilen oder Spalten w i d dasjenie NNE als Pivot-Element ausgewählt da die ingste
Markowitzzahl fwei nd die chwellwebedingu füllt
Zur Ü e r p f u n g der Schwellwertbedingung mu de größte Bet in eine Zeie be
timmt weden Um dies nicht für jedes untersuchte NNE r n e t zu bestimmen wird ein
eld axabs v e l t e t . Ein Wert axabs [i] 0 zeigt an daß der größte Bet in der
ten Zeile nicht bekannt is mmer wenn e b e c h n e t wird, w i d e in axab [i] einge
tragen. Ändert sich abe etwas an der i t e n Z e i , so w i d wiede axab [i] = -1 g e t z t
Dadurch w i d das Maximum imme ur dann timmt wenn e e n ö t i t w i d vo
ch nicht echnet wurde
Eine weitere wesentiche Eienschaft de Implementierung für S o e x ist, da sie gleich-
zeiti ein Maß für die Stabilitt de LU-Zerlegung bestimmt. Daz w i d da Maximum
m a x j l ß l } mitgrechnet nd auch ei den im folgenden Abchnitt z beschreibenden Up-
date der LU-Zerlegung ktulisiert. Falls nach efolgter Fktoriierung keine hinreichende
S t a i l i t t erreicht wurde wi die LU-erlegun mit erhöhtem Parameter u w i e d e h l t
Dies wird so lange iterier, bis entweder eine stabil Zrlegung g f n d e n der mit u —
eine patielle PivotSuche wendet wurde Letzte itt in de P x i nur sehr s t e n
ein
1.7.4 Lösng v n G l e i c h n g e m e m t D r a t r i z
Wie im vorigen Abchnitt schieben müssen zur ösu von linearen Gleichungssystemen
ei gegebener L U - r l e g u de Matix B LU Gleichngssysteme mit den p e t i e t e n
Dreiecksmatizen nd t weden ür eichgssysteme der F ( ind
die
11
nd H
wofür nun die zugehören Algorithmen die Vowä und Rückwärtssubstitti da
tellt werden Die entsprechenden Algrithmen für Geichngssysteme der F r (110
t man einfach durch T a n i t i nd weden d e h a nicht nähe b c h i e e n
Betachte zunächst die L s u n des System (1.116) wobei L eine untere Deiecksmatrix
mit D i a n a l e m e n t e n 1 sei. Der L ö s u g s l g r i t h m u s arbeiten in n Schitten wobei n die
Dimensio von L Ausgehend von y wid in jedem chritt a k t s i e , wobei
jeweils ein weite Eement de Lösungsveors von (1.116) beechnet wird. Dabei wir
ausgenutzt, da ween de D e i e c k s g t a vo jeweils eine eile mit nur ch eine
Unkannten](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-93-320.jpg)

![1.7. LÖSUNG LINEARER GEICHUNGSSYSTEME MIT DER BASISMATRIX
1.7.5 Bas-Up
n jeder Iteration Simplex-Algorithmen sin zwei linare Gleichungssysteme mit der
Basismatri zu lösen, wobei sich diese von Iteration zu Iteration ändert. Jedesmal ei neue
LU-Zerlegung zu berechnen wäre zu aufwendi, zumal sich die Basismatri nur in einer
Zeile oder Spalte genüber der aus der vrigen Itertion unterscheidet und es geeignete
Verfahre gibt, um die alte LU-Zerle weiter zu verwenden. Zwei slcher sog. LU
Uates nämlich die duktform F) [29] nd der ForestTomlin Update [46] in der
Implemetierung nach [93], werden in diesem Abschnitt am Beisiel des in der iteratur
üblicheren Falles e i e s Spaltentausches beschriebe. Beide wurden für SoPlex implemen-
tiert, d s zweite ween seier besonderen Effiziez [46] nd PF wegen seiner Anwendun
beim parallelen Simple l. Abschitt 2.2.3) Nicht imlementiert wurde das Verfahre
von Bartels und G l u b 10 mit sei Weiterentwicklu [84, 86] oder sezielle Upd
teverfhre für V r c u t e r
Betrachte die Matri B, zu der die LU-Zerlegng B LU bekannt sei ie Matrix
B' BV, mit V (I + (B~1r — efief eht aus B durch ustausch der /-ten palte mit
dem Vektor hervr. Das Ziel ist es, ei Verfhre zu fnden, mit dem G l e i c h u s s s t e m e
mit B' unter V e r w e d u g der LU-Zerle e l s t werde könn
Das u r s p r ü l i c h e Verfahren, d s für SimplexAgorithmen verwendet wurde, basiert
auf (der t r a n s p i e r t e n Version v n ) Gleichung (18 Damit kann man Gleichungssysteme
der F r m B = b lösen, i d e m an zuächst Bx b mit der bekannten LU-Zerle
st u anschließed
- e (111
bestimmt. Dabei wird der V e k t r B r ohehin als A / im Simplex-Agorithmus berechnet
Bei mehreren U p d t e s müsse ntspreched iele Krrekturschritte nach (1118 durch
eführt werde
hrend das obige Verfhren die LU-Zerlegun von B aufrechterhält, wird diese durch
da nun zu beschreibende Verfhren v F r e s t u d Tomin anipuliert. Betrchte d z u
die LU-Zerle nB i der (1112) eleitete rm
U7
wobei PU eine obere Dreiecksmatrix ist Da ft iele Spalten von L mit der Eiheitsma-
trix ü b e r e i s t i m m e , s i d meist w e i e r ls ang1-Matrize Lj öti
Betrchte L V.
+iB-ef
U B U .
U.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-95-320.jpg)


![KAPITE 1. REVIERTE SIMPEXRITHMEN
1. Tips und Tricks
Nachdem de o r i g n Abschnitten die r u d l a g e n für eine numerisch stabile Imple
mentierung v sisdrstellungsunabhängigen SimplexAlgorithme z u s a m m e g e t r a
wurden, solle nun einge Kniffe vorgestellt werden, mit d e e n die Geschwindikeit und
Stabilität der mplementierung gesteigert werden kann Von zentraler B e d e u t u g für die
Effizienz ist i jedem Fall die s g f ä l t i Auswahl und Implementieru der z u r u d e
l e t e n D a t e p e , die i A b s c h i t t 3. estellt werde
1.8.1 Skalierung
ie Zahlenwerte in der Nebenbedingungsmatrix eines Ps k n n e n von unterschiedlicher
G ö ß e n r d u n g sein. Dies kann zu LU-Zerlegungen der B s i s m a t r i z e n mit einer schlechten
S t a b i l i t t führen, da die Schwellwertbedingung (1.115) kaum Wahlmöglichkeiten zuläßt
Durch sog. Skalierung kann die Stabilität der LU-Zerlegung verbessert werden. Dazu wird
die Matrix von rechts und links mit Dagonalmatrizen so multipliziert, daß die NNEs der
skalierten Matrix möglichst eng b e i e i n n d e r liegen. Dadurch erhöht sich die Wahlmöglich
keit bei der S c h w e l l w e r t P i t s u c h e , w s zu einer besseren S t b i l i t ä t führt
Die Berechnung solcher Skalierungsmtrizen für jede Basismatrix und ihre Multiplika-
tion würde jedoch einen e r h h t e n Rechenaufwand bei der LU-Zerlegung der B a s i s m t r i
und der Lösung der l i n e r e n Gleichungssysteme bedeuten. U diesen zu vermeiden, ver-
sucht man, das gesamte P skalieren, s d ß beliebige Basismatrizen bereits gut skaliert
sind. Dazu multipliziert man je eine D i a g o l m a t r i x R und C von rechts und links an die
Nebenbedingungsmtri des LPs A, d m i t ßenunterschiede der Zahlenwerte in RAC
nivelliert werden
min min cC
t I < t l < RAC
Es wurden verschiedene Ansätze zur Aufstellung der Diagonalwerte von C und R vor
geschlgen [96, 28, 48]. Einfache Skalierungsverfahren d i i d i e r e n jede eile des LPs mit
einem aus der Zeile gewonnen Wert, wie den Wert mit m a x i m l e m Absolutbetrag (Equi
librierung) oder dem geometrischen oder rithmetischen Mittel aller NNEs der Zeile. An
schließend wird jede Spalte entsprechend skaliert. Derartige Verfahren haben einen geringen
R e c h e n u f w n d , denn jedes NNE der Nebenbedinungsmatrix wird nur z w e i m l verwendet
Neben solch einfachen Methoden gibt es ufwendigere Verfahren, die die „Gleicha
tigkeit" der NNEs ptimieren: Das Verfahren von FulkersonWolfe [48] löst ein Optimie
r u n g s p r b l e m zur Minimierung der ifferenz zwischen maximalen und minimalen NNE.
Dagegen bestimmt das Verfahren von Curtis und Reid [28] die S k l i e r u n g s f k t r e n s , d ß
die V a r i n z der NNEs des Ps minimiert wird.
Aus verschiedenen Tests schließt Tomlin in [96] daß die Skalierungsverfahren nur einen
geringen Einfluß uf die S t b i l i t t des S i m p l e x A l g r i t h m u s h b e n , jedenflls für hl](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-98-320.jpg)
![1.8 TIPS UN TRICK
modellierte LPs. Um den Agorthmus or schlechten PModellen abzusichern, sollten
hingegen einfache Skalierungsverfahren ausreichen. Deshalb wurde für S P l e x ähnlich wie
für CPLEX 15] lediglich ein Equilibrierungsverfahren implementiert, d jedoch im Ge
gensatz zu C L E X uch abgeschaltet werden ann. Darüberhinaus bietet SoPlex die Wahl
b zuerst die Zeilen der zuerst die Splten skliert werden sllen. W s günstiger ist hängt
n dem zu lsenden LP b.
ber den Stbilitätsspekt h i n u s wird häufig als Argument für eine Skalierung des
LPs och eine mögliche Reduktin der Anzahl der Simplex-Iterationen gennnt [96]. In
der Tat kann die Sklierung einen Einfluß auf die A n z h l der SimplexIterationen h b e n .
Dieser k n n sich j e d c h s h l p s i t i ls uch negati uswirken ( g l bschnitt 4 . 6 )
1.8.2 uotientntes
ie bereits in Abschnitt 1.3 bemerkt wurde, ist die stbilisierte Variante des „Textbook"
Quotiententests oft hinreichend stabil. Mit nur einer P h s e ist sie effizienter als zweiphasige
Varianten. Die mplementierung des stabilen SoPlex Quotiententest bricht deshalb direkt
nach der ersten Phase b, wenn das Qmax bestimmende Element bereits zu einem Pivo
Schritt hinreichender Stabilität führt. Solch eine Wahl entspricht bis uf d s Shifting dem
stbilisierten Textbook"Qtiententest
Darüberhinaus speichert der SoPlex Quotiententest in seiner ersten Phase die Indizes
der NNEs von Ax. Dadurch kann in der zweiten P h s e direkt auf die NNEs zugegriffen
werden, und unnötige Zugriffe auf Nullelemente werden vermieden. Auch wenn keine zweite
Phase benötigt wird, wurden die Indizes der NNEs n A nicht unnötig gespeichert; sie
werden in jedem F l l beim Update benutzt
Für die meisten LPs liefert der S P l e x Quotiententest mit festem Toleranzparameter
5 eine hinreichende Stabilität. Dem Autor liegen j e d c h LPs10 v r , bei denen erst zwei
weitere Techniken zur erfolgreichen Lsung verhelfen. ies ist zum einen die dynamische
Toleranzanpassung und zum nderen d s Zurückweisen n P i t E l e m e n t e n .
Für das Zurückweisen von Pivot-Elementen wird ein weiterer Parameter minstab ein
geführt. Führt der Quotiententest zu einem PivotSchritt mit Asq <minstab, so wird
kein Bsisupdate durchgeführt, denn ein solcher würde ach Satz 29 zu einer zu schlecht
nditionierten B s i s führen. Stttdessen wird direkt zum Pricing-Schritt 1 übergegangen,
wo ein neues Pivot-Element gewählt wird. Dabei werden Vrkehrungen getrffen, die eine
erneute Wahl desselben Elementes vermeiden.
Ein zurückgewiesenes Piot-Element zeigt somit an, daß sich der Simplex-Algorithmus
in einem numerisch problematischen Bereich des zugrundeliegenen Polyeders bewegt. Des
h l b wird der T l e r n z p m e t e r S ( d m i s c h ) herufgesetzt um eine grßere Wahlfrei
10
Diese besonders schwierigen LPs dürfen leider nicht weitergegeben werden nd w r d e n deshalb a c h
nicht z r Bewertng der Implementierng in Kapitel 4 herangezogen.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-99-320.jpg)

![1.8. TIPS UN TRICK
1.8.4 Zelen- vers Spalnbas
Die Möglichkeit, sowohl eine Zeilen- als auch eine paltenbasis zu verwenden, erlaubt es
bei der Dimesion der Basismatrix zwischen der Anzahl der Spalten oder der Anzahl der
Zeilen der Nebenbedingsmatrix des Ps zu wählen. Dabei sollte die kleiere Dimensio
vorgezogen werden, da so die ösung der lieare Gleichungsssteme ei eringere
Recheaufw erfordert
D a r ü e r h i a u s kann die Wahl der asisdarstellung einen Einfluß auf die Wahl der Pricer
h b e n . E i i g e Pricing-Strategien, insesondere das partial multile ricing, sind nur für
e i n f ü n d e Algorithmen sinnvoll. Weiß man nun zusätzlich, ß ein LP gnstiger mit einem
dualen als mit einem primalen Algorithmus elöst wird so kann dieses ricing-Verfahre
dennoch eingesetzt werden, dem die Zeilearstellung verwedet wird
1.8.5 Refaktorisierung
Wie i Abschnitt 7.3 dargelegt wird zur Lösung der bei SimplexAlgorithmen auftre
tenden Gleichungssysteme eine LUZerlegung der Basismatrix vorgenommen. Nach e i e m
Basistausch wird i.a. nicht wieder eine ölli neue LUZerlegung berechnet, sondern die
stehende in einer der in 1.7.5 beschrienen Arten manipuliert. Nun stellt sich die
wie oft solche Updates sinnvoll s i . D e i ist zweierlei zu e r ü c s i c h t i n :
die Stailität der torisierung
die Gesamteschwidigkeit des SimplexAorithmus
Dem ersten Punkt muß stets Vorrang gewährt werden. Deshalb wird wie in 1.7.3
schriebe die Stabilität der Faktorisierung überwacht und bei Überschreiten eines Gre
wertes eine neue LUZerlegung der asismatrix berechet der axis hat sich ei Gre
6 8
wert i der G r o r d n g 10 — 0 ewährt
Der zweite kt ist immer dann zu beachten, wenn die Stabilitätsforderung oh
nehin erfüllt ist, u dies ist bei über 90% der dem Autor vorliegende LPs der Fall
Somit lohnt sich ein genaueres Studium des Geschwindigkeitsaspektes [26] wird dies
unter statische Voraussetzungen durcheführt, was zu einer konstanten Faktorisierungs
frequenz führt. In [6 wird die „optimale kostante Faktorisierungsfrequez a n h n d eines
Testlaufes bestimmt. SoPlex verfolgt hingegn e i n dynamischen Ansatz bei dem der op
timale Zeitpunkt der erneute L U Z e r l e n g der asismatrix a a n d des eweils aktuelle
Zustads bestimmt wird
Da i . bei edem Update der Faktorisierung zusätzliche Werte espeichert werden,
die bei anschließe gelöste Gleichungssystemen bearbeitet werden müssen, wächst mit
edem Update der ufw zur Lösung vo Gleichungssstemen. Ziel ist es daher de](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-101-320.jpg)

![1.8. TIPS UN TRICK
1.8. artbas
Für allgemeine L der Form (1.45) ist Z P,Q), mit { l , . . . , n } und Q =
n + . . . ,n + m} eine mögliche Startbasis zum zuehörige Phase-1-LP, die Schlupf
basis genannt wird. E kann jedoch zur Reduktion der gesamten Iterationszahl von Vorteil
sein, auf heuristischem Weg e i e bessere Startbasis zu konstruieren, die sich weniger von
e i e r zulässig und optimalen asis unterscheidet Solch ei Verfahre heißt e i e Crash-
zedur die erierte Basis e i e Crash-Basis.
uch für S o l e x wurde eine CrashProzedur entwickelt, die sich stark an [15] orientiert
d nun für eine Basis i Zeiledarstellung vorgestellt wird. Sie arbeitet in drei asen.
der ersten Phase, wird eder Zeile von (1.5) ein Präferenzparameter CJ, (i = 1 , . . . , n +
m) zugewiesen, der eine Präferenz für die Aufnahme der i t e Zeile in die Basismatrix
arstellt. A s c h l i e ß e d werden alle Zeilen nach a b e h m e d e m äfereparameter sortiert
schließlich r e e d a r t i ei asis konstruiert
ie Festsetzung der räferenzparameter erfolgt auf heuristischem W e . Dazu überlegt
man sich welche Bedingng / < a < u eher in der asis sei sollte nd welche eher
nicht. So werden Bedingungen mit / —o u +oo eher selte der optimalen
asis zu finden sein, wohl aber Gleichunge (l u). Allgemein wird an vermuten, daß
je größer der Wert l — u ist desto wahrscheinlicher wird die zuehöri edingng eier
zulässi optimalen Basis zu de sein.
Dieses heuristische rgument berücksichtigt zwar die S c h r k e n der Bedingngen, nicht
aber die Zielfunktion. bbildung 1.1 le jedoch nahe, daß i einer optimalen Basis eher
Nebenedingungen zu finde si dere ormalenvektor ei ering W i k e l zum iel
fuktiosvektor aufweisen.
Schließlich sollte auch die numerischen Eigenschafte der zu konstruierenden Startba
sis Berücksichtiung finden. Dabei sind (Vielfache von) Einheitsvektoren numerisch beson-
ders gutarti d sollte deshalb Vektore mit mehreren Nichtnullelemente vorezo
werden.
iese drei Aspekte werden durch die f o l g d e Initialisierung der P r ä f e r e a r a m e t e r
10
aufgegriffen. Sie verwendet e i n Strafwert M der z.B. auf eine Wert vo
esetzt wird ür die ite e b e d i n g n g lf f < uf setze zuächst
falls lf uf
lf uf falls lf uf
falls
falls lf uf
sost
falls f ei skalierter heitsvektor ist
sost](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-103-320.jpg)


![apitel
arallelisieru
Aufgrund der wirtschaftlichen Bedeutun der Linaren Progammierung ist es nicht ver
wunderlich daß es bereits verschiedene Untersuchungen g e b hat, wie LPs durch Nut
zung von Parallelität schneller gelöst werden könnn. Ei utoren beschreiben par
allele Implementierung des S i m p l e x o r i t h m u s , währe a d e r e spezielle Varinte
B. NetzwerkSimplex [9]) oder völlig andere orithmen zugrundeleen [97,
wird s o a r ei spezieller arallelrecher für Probleme v o r e s c h l n .
In der Literatur zur Parallelisierung des SimplexAlgorithmus gibt es Veröffentlichun-
gen, die LPs mit spezieller Struktur betrachten, die für e i e Parallelisierung nutzbar g
macht werden kann [51, 74] Die Mehrzahl der Publikationen befaßt sich jedoch mit dem
üblichen primalen SimplexAlgorithmus. Allerdings gibt es bis auf [13] kein Arbeit die zu
einer Implementierung führt, die mit stateofthe-art sequentiellen Implementierungen kon-
kurriere könnte. ies l i e t zum eine aran, daß entweder vom SimplexAorithmus in
TableauForm ausgegange wird [20 9 8] oder zum andere die vorgestellten Implemen-
tierungen auf dichtbesetzte Vektoren d Matrizen operiere [91, 78, 43]. Mit dnnbesetz
te Matrizen arbeiten hingegen die in [62, 58, 59] vorgestellte Implementierungen. Jedoch
ist nicht ersichtlich, ob tatsächlich ein leistungsfähiger Code entwickelt wurde. Dies ist nur
für [13] sicherestellt wobei sich die Parallelisierung jedoch nur auf das MatrixVektor
Produkt beim duale SimplexAorithmus mit S p a l t e a s i s b e s c h r k t (vg bschitt
1).
In diesem Kapitel werden die SMoPlex nd oPlex zugrudeelegten arallelisierungs
nsätze vorgestellt Z ä c h s t wird in Abschnitt 2 1 eine kurze Einführung in das Gebiet des
Parallelen R e c h n s geeben, wobei den drei zentralen Aspekten, nämlich der Zerleung
von Algorithmen in nebenläufig bearbeitbare Teilprobleme, den wichtigsten Klasse vo
arallelen HardwareArchitekturen sowie den hier zum Ensatz kommenden arallelen Pro
rammiermodellen je ein TeilAbschitt ewidmet wird. Schließlich werden in Abschnitt
1.4 die wichtisten G r u d b e r i f u s a m m e n g für die eurteilung aralleler
orithme vorestellt](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-106-320.jpg)
![1. GRUNDLEN DER PALLELVERRBEI
Die n u t z a r e N e b ä u f i g k e i t im SimplexAlgorithmus wird Abschnitt 2.2 heraus
gearbeitet. In je einem Unterabschnitt werden dort die parallele Berechnung des Matrix
VektorProduktes, die Parallelisierung des Pricings und Quotiententest, das B l o c P i v o t i n g
sowie die gleichzeiti Lösung zweier linearer Gleichungsssteme beim steepestedge Pricing
erklärt. Abschnitt 2.25 faßt die Parallelisierungskonzepte han eines L a u f z e i t d i a a m m s
noch einmal zusammen. Schließlich behandelt Abschnitt 2 3 die parallele ösung dünnbe
setzter linearer Gleichungsssteme auf asis e i e s arallelen L Z e r l e n g o r i t h m u s '
2.1 Grundlagen der Paralelverarbeitung
is heute hält eine intensive Jagd nach immer schnelleren Rechnern an, um damit immer
rößere Probleme zu lösen. Als Faustregel gilt eine Verdopplung der Recheneschwindikeit
lle M o n t e . Doch wie l g e noch ist diese ntwicklun fortsetzbr?
Vom theoretischen Standpunkt aus ist die Lichteschwindigkeit als bsolute Grenze
jeder Signlübertragung eine wenn auch noch lange nicht erreichte Schranke für
die Rechengeschwindigkeit. Technisch wird es jedoch schon heute immer schwieriger, noch
höhere Taktfrequenzen zu realisieren, da bei Frequenzen im Mikrowellenbereich die Lei
terbahnen innerhalb einer i n t e r i e r t e n Schaltung induktive und kapazitive W i d e r s t n d e
darstellen die d s logische Verhalten des Chips stören können. Mit immer höheren Takt
frequenzen llein können also schon heute d e r a r t i e Beschleuniungen nicht mehr erzielt
werden. Ein Ausweg ist die Ausnutzung von Paralllität, d h das leichzeitige Zusammen
rbeiten mehrerer Funktionseinheiten um so mehr esultate pro eit zu erechnen
Vom normalen PC oder WorkstationNutzer unbemerkt wird schon heute bei llen
moderen Computern arallelität ausgenutzt nämlich innerhalb von RISC (reduced in
struction set computer Prozessoren. Vereinfacht sind zur usführun eines ISCBefehls
vier Teilschritte die so RISCPipeline erforderlich [ 8 ]
1. fetch: aden des efehlsbytes
2. decode estimmung des auszuführenden efehls
3. execute usführun der Operation
write Rückschreien der bnisdaten
Jeder dieser Schritte erfordert einen T k t z y k l u s so daß ein einzelner Befehl erst nach
4 Zyklen tatsächlich abgearbeitet ist. Beim Pipelining werden die Teilschritte ufeinander
folgender Prozessorbefehle so ineinander verschachtelt daß n c h den ersten ktzyklen
mit jedem kt ein neues R e s u l t t produziert wird g . Abb 1)
Ähnliche Prinzipien werden bei modernen Prozessoren immer weiter ausgenutzt. Mehre
re Pipelines rbeiten arallel superpipelined architecture), es werden mehrer arithmetische
Einheiten parallel eingesetzt (superscalar), bei V e r z w e i g u n n w e i s u n g e n wird jeder Zwei
in einer Pipeline weiter bearbeitet, wobei nicht benötigte Ergebnisse dann verworfen wer
den s p e c u l r execution und vieles mehr uf ll dies soll nicht tiefer e i n g a e n werden](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-107-320.jpg)






![KAPITEL 2 PALLELISIERUNG
Diese Schrnke ist nur theoretisch zu vertehen. Im Normlfall wird si ncht erreicht,
weil durch zusätzlichen Aufwand b der Parallelisierung (etwa zur Kommunikation oder
n c h r o n i s o n ) z u t z l c h Ze vereht, n der ken Betrag zur un eleistet wrd.
D Schrnke kann aber uch erschritten werden, ja sogar ne superlneare Beschleu-
nigun ist mölich. Dies lie Cache heutiger Computerarchitekturen. Typischerweise
verfügt jeder Prozessor enes Prallelrechners auch über eigenen Cache (d gilt cht für
den T3D von CRAY). Dadurch können bei mehreren Prozessoren mehr Daten ache
gen und somt schneller betet werden, n enzelner rozessor (m nem
chrnkten Cche) n der age w r e .
Dem etwas entmutigenden Amdahl'schen Gesetz, daß e Skaierbarkei rk ein-
schränkt, setzte Gustavson ne Beziehun e n t e n , d e d e Nützlichket de allelen
Rechnen für die Berechnung größerer Probleme bechreib scale-up) [56]. Dabei geht er
davon , daß sich m Übergang zu größeren Probleminanzen a. der p a l l e l e Antei
der A r i t erhöht, se equentieller Anteil jedoch konstnt leibt. Wenn so auch die Be-
chleunigung bei der Löun nes Prolems b c h r ä n k t leibt, o e r m ö c h t P l l e l
e Löun rößerer r o l e m n z e n .
SATZ 33 (GUSTAVSON'S GESETZ)
i N in Maß für e Größe iner Probleminsanz. Se Ts T0 +
Zit de ein inzelner roessor u dessen Lösung beansprucht, wobei Xj Np
de parallelisierbare ntl beichet und der inherent sequentielle Antl T0
nt sei. Dn i it Proessore errechre Beschleunigng
EWEIS:
Für p Prozessoren gilt Tp T0+T/p = T0 + N wor it (2. S = (T0 + Np)/(T0 +
p+l- p)T0/(T0 + p+1- p)T0/ ween p folt.
•
Ende der 80er J h r e veruchte Gustavson t sener Bezehun einen mental lock ge-
en „massive P a r l l e l t ä zu bekämpfen [56]. Zu dieser Zeit erwrtete m für die Zukunft
Parllelrechner, d au tausenden bis mllonen Prozessoren zusammengeetzt sind. Heu-
te h man von desen Vorstellungen weitgehend b s n d enommen und verteht unter
assiver P l l e l t ä eher e i g e Hundert PE
n definert ferner d e Efizinz ne llelen A l o r t h m
- (2.3
p
Sie ist ein M ß dafür, n wi weit d e PE eine Parallelrechners t a c h l i c h genutzt wer
den. Der B e i f f der Sklierbkeit chreibt, wie sich d e Effizienz mi zunehmender ro
zessoranzahl verhält: Ein parllele r o a m m heßt erbar, wenn ne Effizenz
nzunhme weterer PE nur wenig a b m m " .](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-114-320.jpg)


![BENLA UF EX-GORITHM
vorgenommen: Jedes PE berchnet de Tel de Matx-VektorProdukts, zu de es di
Vektoren von A eichert.
Das mit der Verteilung des LPs und damit der Arbeit g e m ß (2.5) ein vernünftiger Last
ausgleich erzielt wird, entspricht der Beobachtung, daß meist ähnliche Strukturen des LPs
in der Nebenbedingungsmatrix nahe beieinander zu finden sind. Jede Struktur wird daher
gleichmäßig auf alle PEs verteilt, so daß jedes PE von jeder Struktur einen Teil verwaltet.
Dadurch wird insbesondere auch vermieden, daß einige PEs nicht an dem Lösungsprozess
teilnehmen, weil sie zufälli an den relevanten Strukturen nicht artiziieren. Davon wird
in Abschnitt 2.2.3 noch die Rede sein.
Die Version für Parallelrechner mit gemeinsamem Speicher, SMoPlex, arbeitet auf der-
selben Datenstruktur wie die sequentielle Implementierung SoPlex. Dadurch wird eine Ver-
teilung der Arbeit von (2.4) gemäß (2.5) nicht mehr sinnvoll möglich. Sie würde es erforder
lich machen, daß die Matrix spaltenweise traversiert wird, und jedes Ag, als Ag, = AhT -AA
berechnet wird. Da aber Ah in der R e e l dünnbesetzt ist, werden so mehr Rechenoera-
tionen durcheführt, als wenn man
A
Ag ^ M*
berechnet.
Um solch eine zeilenweise Berechnung auch im parallelen Fall durchzuführen, ist es
sinnvoller, A in Blöcke zu unterteilen, die jeweils zeilenweise bearbeitet werden. Die Blöcke
werden dabei so erzeugt, daß in jedem Block etwa gleichviel NEs sind. In der R e e l
entstehen so Blöcke mit unterschiedlich vielen S a l t e n von A.
2.2.2 Paalleles ricin und Q u o t i n t n t e s
Beim Pricing und Quotiententest handelt es sich um einen einfachen Suchalgorithmus, bei
dem aus einer M e n e von Werten ein maximales (bzw. minimales) Element bestimmt wird.
Die Parallelisierung solch eines Suchalgorithmus liegt auf der Hand. Man zerlegt die Men-
ge in Teilmengen, aus denen jeweils ein PE das maximale (minimale) Element bestimmt.
Anschließend wird von den p Elementen das beste ausgewählt. Diese Auswahl kann mit ver
schiedenen Algorithmen erfolen, wobei der ünstiste jeweils von der zurundelieenden
Hardware a b h ä n t
Im verteilten Fall, ist die Aufteilung des Suchraumes bereits durch die Verteilung des
LPs und damit einhergehend von den Vektoren g und Ag vorgegeben. Hat nun jedes PE
das lokale maximale bzw. minimale Element bestimmt, gilt es, aus diesen p Kandidaten
das global beste zu finden und allen PEs bekanntzugeben. Einen Algorithmus der solches
leistet nennt man Gossiping. Eine optimaler Algorithmus für dieses Problem 73] ist als
Algorithmus 11 für das ite von p 2P PEs anegeben. Die anderen PEs führen gleichzeitig
denselben Alorithmus aus, wobei i die jeweilie PE-Nummer ist. Die Operation c = a xor](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-117-320.jpg)



![NLA UFKE PLEX-GORITHM 05
Die Vektoren A / und Ag werden bei dem PivotSchritt ohnehin berechnet. Damit
beschränkt sich der Rechenaufwand auf die Addition des Vielfachen eines Vektors und ist
damit wesentlich niedriger als der für die Lösung eines Gleichungssystems. Gleichung (2.7)
wird für den einfüenden Simle benötigt, während (2.6) beim entfernenden Alorithmus
anewendet wird.
Um überhaupt genügend wählbare Pivot-Indizes zu finden, muß die Suche nach den ein-
zelnen Indizes geeignet aufgeteilt werden. Hier hat sich die Verteilung gemäß (2.5) bewährt.
Daggen wurde bei einer blockweisen Verteilung oft nur ein wählbarer Index gefunden,
denn alle wählbaren Indizes liegen häuf nah beieinander und somit in einem Block. Des
halb wird auch bei der Implementierung für Parallelrechner mit gemeinsamem Speicher
die Arbeit nach (2.5) verteilt und somit anders als für die Berechnun des MatrixVektor
Produktes.
Damit im verteilten Fall die PEs überhaupt die Gleichungsssteme lösen können, ist
es notwendig, daß jedes PE auch die Basis-Matrix samt ihrer LU-Zerleung lokal zur
Verfügung hat. Dazu muß der jeweils in die Basis eintretende Vektor allen PEs z u ä n
emacht werden. Dies verursacht einen zusätzlichen Kommunikationsaufwand.
Man beachte, daß Block-Pivoting den Ablauf des Algorithmus beeinflußt. Während
im sequentiellen Fall das Pricing in jeder Iteration den (im Sinne der jeweiligen Pricing
Strategie) besten Index auswählt, werden beim Block-Pivoting zunächst die p besten In-
dizes gewählt. In der (p l)-ten Iteration danach, wird somit der ptbeste Index einer
frühreren Iteration als PivotIndex verwendet. Der sequentielle Pricer würde wahrschein-
lich einen anderen Index präferieren. Inwieweit sich dies auf die Anzahl der Iterationen
auswirkt, hängt von dem zu lösenden LP ab. Im allgemeinen wird man eine Erhöhun
erwarten, aber auch Verbesserunen werden beobachtet.
Einen nicht zu vernachlässigen Nachteil hat das Block-Pivoting in Bezug auf die LU-
Updates der Basismatrix. Da beim einfügenden Simlex nicht mehr vor dem Einfügen
eines Vektors in die Basis das Gleichungssystem B gelöst wird, steht auch der Vektor
Lxr nicht zur Verfügung, der für den Forest-Tomlin Update notwendig ist. Diesen Vektor
explizit neu zu berechnen, impliziert einen nicht vertretbaren Rechenaufwand, so daß beim
Block-Pivotin für den einfüenden SimlexAlorithmus der PF U d a t e benutzt werden
muß.
M. Padberg gibt in [80] eine andere Interpretation für das Block-Pivoting. Dabei steht
die Frage im Vordergrund, wie der einfügende SimlexAlgorithmus umzuformulieren wäre,
wenn pro Iteration statt nur einem Pivot-Index eine M e n e C von PivotKandidaten
gewählt würde. Am Ende der Iteration erwartet man eine optimale und zulässie Basis
für das LP, das aus der Anfangsbasis und der Kandidatenmene besteht. Für C
entspricht dies gerade den üblichen Gegebenheiten, während für C n das gesamte LP
mit nur einem Block-Pivot gelöst wäre. Die gesuchte Basis erhält man, indem man das aus
der aktuellen Basis und C bestehende LP löst, für das die aktuelle Basis als Startbasis ver
wendet werden kann. Zur Lösun dieses Sub-LPs s c h l t Padber das SimleVerfahren](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-121-320.jpg)



![PALLELE LOSUNG LEICUNGSSYSTEME 109
ein Parallelrechner mit verteiltem Speicher. Da die Synchronisationszeiten derzeitige
MultiprozessorWorkstations die Kommunikationszeit des Cray T3D übertreffen, wurde
auf eine Implementierung für Architekturen mit gemeinsamen Speicher verzichtet. Im fol
genden wird deshlb direkt der Algorithmus für Architekturen mit verteiltem Seicher
vorgestellt.
2.3.1 arallele L U e r l e g u n g
Das Verfahren der LU-Zerlegung wurde bereits mit Algorithmus 7 beschrieben. D b e i liegt
der hauptsächliche Rechenaufwand im U p d t e L o o p , ber auch die PivotAuswahl und
der L-Loop benötigen eine gewisse Zeit. Die nutzbare Parallelität in diesen drei Schrit
ten hängt von der Verteilung der Daten auf die PEs ab. Sie wird in Abschnitt 2.3.1.1
vorgestellt. Ähnlich dem Block-Pivoting beim Simplex-Algorithmus können auch bei der
LU-Zerlegung dünnbesetzter Matrizen bei gewissen Gegebenheiten mehrere Iterationen zu
einer „Block-Iteration zusammengefaßt werden, die zusätzliche Nebenläufigkeit bietet. Die
dazu nötige Kompatibilität von PivotElementen und deren Ausnutzung wird in Abschnitt
2 . 3 . 2 erläutert. Schließlich wird in Abschnitt 2.3.1.4 ein neues Verfahren zum d y a m i
schen Lastausgleich vorgestellt, ß ohne zustzliche Kommuniktion oder Snchronistion
uskommt.
2.3.1.1 Datenvereilung
Die Verteilung der Daten auf die PEs bestimmt die nutzbare Nebenläufigkeit und sollte so
erfolgen, daß alle PEs in etwa dieselbe Last erhalten. Es gibt zwei gundsätzliche Ansätze
für die Datenverteilung. Bei einem wird die Beseztungsstruktur der Matri a n a s i e r t und
uf dieser Grundlage eine günstige Verteilung ermittelt, die ein Maximum n Prallelitä
und in Minimum an entfernten Datenzugriffen gewährleistet [61]. Dieser Ansatz ähnelt den
Verfahren der Fillminimierung bei der LU-Zerlegung, bei denen die Permutationsmatrizen
vor der Faktorisierung ermittelt werden. Deshlb eignet er sich uch besonders für solche
Verfhren.
Beim zweiten Ansatz wird eine feste Verteilung der Daten auf die PEs zugrundegelegt
[49, 9]. Dies erfordert ggfs. einen dynamischen Lastausgleich. Da beides ohne zusätz
lichen Rechen- und Kommunikations- bzw. Synchronisationsaufwand erfolgen (vgl. Ab-
schnitt 2.3.1.4) k n n , wurde dieser Ansatz verfolgt. In [85] wurden verschiedene (feste)
Verteilungsschemata von Zeilen und Spalten auf PEs untersucht, wobei eine gitterartige
Verteilung zu einem besonders geringen Kommunikationsaufwand führt. Deshlb wurde sie
wie in [89 uch für die hier vorgestellte Imlementierung verwendet.
Seip = rc die Anzahl der verfügbaren PEs. Die PEs werden logisch ls ein rx Gitter
angeordnet (vgl. uch Abb. 3.16), und deshalb mit (kl) für 0 < k < r und 0 < l <
bezeichnet. Jedem atrielement B^ wird einem PE zugeordnet, d s es seichert, sofern](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-125-320.jpg)
![110 KAPITEL 2 PALLELUNG
es von Null vechieden ist. Die Zuordnung von elementen zu Es erfolgt gemä
pe(i (i mod mod c) 2.8)
d.h. das atrixelement B^ wird auf dem PE (i mod r, j mod c) gespeichert. Jedes PE
verwaltet also eine (dünnbesetzte) Submatrix, wobei dieselben Datenstrukturen wie bei
der sequentiellen Implementierung verwendet werden. Die Verteilung (2.8) erschließt P r
allelität beim UpdateLoop, beim L-Loop, bei der PivotAuswhl und bei der Berechnung
der m i m l e n Absolutbetrge ro Zeile.
In [101] wurde eine Implementierung vorgestellt, bei der lediglich die Zeilen auf die
PEs verteilt wurden, jedes PE aber lle Spalten verwltet. Diese Verteilung benötigt we
niger Kommunikationen als (2.8) da u.a. die Maxima in jeder Zeile von jedem PE ohne
Kommunikation mit anderen bestimmt werden können. Deshalb eignet sich diese Imple
mentierung besonders für Parallelrechner, die eine hohe Latenzzeit bei der Kommunikation
aufweisen. Die Reduzierung der Anzahl von Kommunikationen erfolgt jedoch auf Kosten
der nutzbren Nebenläufigkeit, w s die Sklierbrkeit dieser Imlementierung einschränkt.
2.3.1.2 Kompatible P v o t - E l e e n
Bei der LU-Zerlegung dichtbesetzter Matrizen ist die nutzbare Parallelität vollständig
durch die Verteilung vorgegeben. Es ist nicht möglich, mehrer PivotSchritte nebenläuf
zu berbeiten, d sich die ktive Submtri mit jedem Schritt ändert.
Für dünnbesetzte Matrizen gilt diese Aussage nicht mehr. Sofern kmpatible Pivot-
Elemente benutzt werden, stören sich die Änderungen der aktiven Submatrix nicht ge
genseitig, so daß solche PivotElemente parallel eliminiert werden können. Ähnlich dem
Block-Pivoting beim SimplexAlgorithmus werden so mehrer Iterationen zu einer lle
len Itertion zusmmengefßt.
DEFINITION 12
Die Elemente B ^ . , Bi einer Matri £ Wixn mit heiße kom
tibel, fall für gil
Biük 2.
Die Submatrix aus den Zeilen und S l t e n von kompatiblen Elementen bilden also eine
D i g o n a l m a t r i . Die Bedeutung von kompatiblen Elementen für die llele LU-Zerlegung
dünnbesetzter atrizen wird von dem folgenden Satz beschrieben.
SATZ 35
1
eien £>jUl ^ 0 nd Bi2j2 ^ 0 kompatible Elemente einer Matri
Nach Eliminati beider Elemente gil
B3 B- BjlBi B nBh
' 2.10](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-126-320.jpg)
![PALLELE LÖSUNG LEICUNGSSYSTEME 11
nabhngi der Eliminatinsreihelge B^ nd Bi
EI
Wir zeigen (2.10) für die Elimintionsreihenfolge Bi B i . N c h Schritt 3 und 5 von
Algorithmus 7 gilt
B B
wobei die l e t e Gleichung us der Kompaibilitätsbeziehung Bixj2 0 Bi2j1 folgt.
Gleichung (2.10) zeigt man analog für die umgekehrte Pivotreihenfolge, wobei die Indizes
und 2 jeweils vertuscht werden müssen.
•
Nach Satz 5 können komatible Elemente in einer beliebigen Reihenfolge eliminiert
werden, ohne daß dies zu einer Änderung der aktiven Submatrix führt. Insbesondere können
verschiedene PEs eine unterschiedliche Reihenfolgen bei der Elimination wählen. Dies kann
man sich für einen parallelen LU-ZerlegungsAlgorithmus zunutze mchen, der weniger
s t r k synchronisiert und somit von gröberer G r n u l r i t t ist.
Konzept der Kompatibilität wurde zunächst in [33] für die Implementierung ei
nes parallelen LU-Zerlegungs-Algorithmus auf Multiprozessoren mit gemeinsamen Seicher
eingeführt. In 89] wurde es für Transputer-Systeme eingesetzt. Für symmetrische Matri
zen hat die Kompatibilität eine einfache Darstellung als sog. elimination Trees, die bereits
früher die Grundlge bei der parallelen CholeskiZerlegung symmetrischer dünnbesetzter
Matrizen bildete 41, 61]. Sie wurden durch Übergang zur symmetrisierten Matri B + B
oder BTB uch auf den unsymmetrischen Fall erweitert [3]. In [33] wird jedoch gezeigt,
daß diese Matrizen meist dichter besetzt sind als B, so d ß mehr Arbeit bei der LU-
Zerlegung anfällt und die durch Dünnbesetztheit gebotene Parallelität reduziert wird. Aus
diesem Grund wird hier ähnlich zu [89] die Kompatibilität direkt uf der unsymmetrischen
Besetzungsstruktur der zu fktorisierenden tri usgenutzt.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-127-320.jpg)



![PARA OSUNG UNGSSYST 11
verbleibende ktive Submatrix heißt der Nukleus der Matrix und enthält keine weiteren
Singletons. Im Nukleus können zwar nach einigen Pivot-Eliminationen neue Singletons ent-
stehen, jedoch geschieht dies i . in so niedriger Z h l , d ß eine s e p a t e Behndlung nicht
mehr lohnt.
2.3.1.4 Lazy L a d n c i n g
Da die zu verrichtende Arbeit mit Abnahme der Dimension der ktiven Submatrix dyna
misch von Iteration zu Itertion variiert, und zwar wohl möglich unterschiedlich uf ver-
schiedenen PEs, muß ein dynamischer Lastusgleich erfolgen. D z u b e d r f es eines M ß e s
für die L s t eines PEs im Vergleich zur G e s m t l s t .
Eine Möglichkeit für solch ein Maß wäre das Verhältnis der Anzahl der NNEs der aktiven
Submatrix eines PEs zur Gesamtzahl der NNEs. Letztere zu bestimmen würde jedoch einen
weiteren Kommunikationsufwand erfordern, der vermieden werden sollte. Statt dessen
wird ein approximtives Maß verwendet, die von einer gleichmäßigen Verteilung der NNEs
auf die Submatrix ausgeht. Dies ist durch die Verteilung (2.8) reltiv gut gewährleistet. Für
jedes P (i) bezeichne r s (i,j) die Anzahl der Zeilen und c(i,j) die A n z h l der Splten
von der ten aktiven Submtrix, die von dem PE verwltet werden. D n n wird die st
des z-ten Es ls
(i (t)-(t,j 2.11
defniert. Wegen ^rs(ij) =n ^2c(ij) ist die G e s m t l s t
= (n)-( 2.1
Die Aufgabe des Lastausgleichs ist es, I (i) Ls/p möglichst gut zu erreichen. Aktive
Verfahren spüren Abweichungen davon auf und transferieren Last von überlasteten PEs
zu unterforderten. Bei der LU-Zerlegung würde dies durch die Übergabe von Zeilen oder
Splten erfolgen, w s zu einem zusätzlichen Kommunikationsufwnd führte.
Dieser kann mit einem ssiven Lastusgleichsverfahren vermieden werden, der in [101]
zuerst vorgestellt wurde. Da in jeder parallelen Iteration Last abgebaut wird, k n n die
Lastverteilung ausgeglichen werden, indem PEs mit einer höheren Last versuchen in der
folgenden Iteration mehr L s t abzubauen als solche mit einer geringern Last. Dies wird
über die Anzahl der P i v o t - n d i d a t e n ks(ij) erreicht, die edes PE (ij) in der -ten
Itertion uswählt
(ij) 2.1
amit werden insgesamt ca K Kandidaten ausgewählt, wozu jedes PE anteilig zu seiner
Last viele beiträgt. Abbildung 2.4 zeigt, d ß d m i t in der t eine bessere Lstverteilung
erreicht wird.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-131-320.jpg)





![3. UNDEN OBJRINTIERTER PRMMIERUNG
dort V a l e öglicerweise a n d w e i t i g b e n z t weden Dies widespricht Anfoderun
3. Ebens kann prinzipiell jeder Punkt in einem Programm von einem beliebigen anderem
a n g e s r u g e werden. Ddurch ist eine Änderung stets mit kaum lkulierbre Risike
v e r b u d e , was wiederum Widersruch zu Anforderung 2 steht [5]
Dieser Problematik wurde durch Bereitstellung weiterer Abstraktionsmittel on
t r o l l f l - und Dateebene begegnet die zur strukturierten Programmierung führte [36. Sie
h t den früheren imperativen Prgrammierstil vollständig abgelöst. Hierbei wird ein Pr
gramm als F l g e strukturierter Operationen (Ausdrücke, Schleif Prozeduren, Blöcke) a
strukturierte Daten (lokale Namesräume, strukturierte D a t e n y p n wie Verbünde u
Reihungen) formuliert. Durch die trukturierung des Namensraum der V r i b l e k n n
sichergestellt werden, daß Variablen nicht i verschieden Zusammenhängen kopati
bel b e u t z t werden, und durch strukturierte Operationn (Schleifen etc.) werden Sprünge
mit den amit verbunden Risike vermieden. Zur Darstellun strukturierter Program-
me werden meist Nassichneiderman Struktogramme verwendet [79 ie ermöglichen eine
übersichtliche D r s t e l l u g strukturierter O e r t i o n e n u d sehe kei öglichkeit zur D r
stellug von S p g e or
Zunächst erscheint die Restriktion bei der Benutzug von Sprngen oder beim Zugrif
a f Daten als hinderlich. Es zeigt sich jedoch, daß z.B. Sprünge geerell durch äquiv
l e t e strukturierte Ausdrucksmittel (wie Schleife) ersetzt werden önnen. Dafür gewinn
an groß Vorteile hinsichtlich der Anforderungen 1-4: (Seiteneffektfreie) Prozeduren etw
könnn in e i e m beliebigen anderen Programm eingesetzt werde nforderug 3), w
zur Entwicklung umfangreicher Fuktionsbibliotheken führte
Dennoch unterstützt auch die strukturierte Prgrammierung icht alle g. Anforde
r u n g e . Isbesondere zeigten sich Mängel bei der Wiederverwendbrkeit. Man denke etw
an e i n Satz von Funktionn, die O e r t i o n e n auf einer komplexen Datestruktur, z.B ei
ner dünnbesetzten Matrix, usführe. Oft wird diese Datenstruktur global zur Verfügung
gestellt, damit alle Funktionen daauf zugreifen können. Dies kann aber zu Kmpatibi
litätsoblemen mit andere SoftwreKomponnten führen, die evtl. dieselbe g l l e
ten anders v e r w e d e , w s zu Ikonsistenze führen kann
Diese Problematik hat zur Entwicklug der modularen Programmierung geführt Sie
stellt zusätzliche Ausdrucksmittel zur Trennung von Schnittstelle und der zugehörigen Im-
lementierung zur Verfügung. Die Implementierung e i e s Moduls umfaßt lle benötigten
tenstrukture nd internen Funktionen zu deren M p u l a t i o n . Au diese kann aber „von
auerhalb" des Moduls nicht direkt zugegriffen werden ielmehr kann nur die Schnittstelle
benutzt werden. Die Mdulschnittstelle ist eine Auflistung aller D e k l t i o n n (Funktionen
Variablen, etc.), die von außerhalb des Moduls angesprchen werde önnen Dementsre
chend stellt sich ein mdulorientiertes Progrmm als eine Menge von odulen dar, die nur
über ihre Schnittstellen i n t e r g i e r e . Die Darstellung eines slchen Prgramms geschieht
mithilfe von dulgraphe i d e n n verschiedene Beziehunge zwische den M d u l e wie
B e u t z t r e l t i o n n oder Kontrllflu rgestellt werde](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-137-320.jpg)



![UNDEN OBJRINTIERTER MMIERUNG
graphen eingesetzt (vgl Abb. 3 ) . Jede Klasse wird durch einen Kasten repäsentiert, und
eine Ableitunsbeziehung durch einen Pfeil von der abeleiteten Klasse zur asisklasse
3.1.2 E i n o r d n u n g von C-—
Die Programmiersprache C + + erfreut sich derzeit weiter Verbreitung, ist sie doch aufgrund
ihrer Ähnlichkeit zu C schnell zu erlernen, und bietet darüber hinaus ein genügendes Ma an
Unterstützung für bjektorientierte SoftwareEntwicklung. Dabei wurde au eine vollkom-
mene Unterstützung aller Leistungsanforderungen der bjektorientierten Programmierung
zugunsten einer Übersetzbarkeit in ebenso effizienten Code wie C verzichtet. Aus diesem
Grund wurde C + + auch für die hier v e s t e l l t e n Implementierungen verwendet.
Ableitung von Klassen wird v n C + + mittels Vererbung realisiert. Dies bedeutet, daß
der Compiler für die abgeleitete Klasse eine Kopie der Basisklasse erzeugt und dieser die
zusätzlichen Methden und internen Daten hinzufügt4
C + + ist wie C eine statisch getypte Sprache und bietet somit kein echtes dynamic
Typing. Es gibt jedoch zwei Ansätze eine Vereinfachung davon zu unterstützen. Zum einen
sind dies parametrisierte (template) Klassen der Funktionen, bei der ein Typ Parameter
sein kann. Damit läßt sich z B . ein Stapel für Objekte einer beliebigen aber festen Klas
se realisieren. Zum anderen eschieht eine automatische Tpanpassung, wenn ein Objekt
einer abgeleiteten Klasse als Parameter übergeben wird, wo eigentlich ein Objekt seiner
asisklasse erwartet wird. Dies ist möglich, da die abgeleitete Klasse stets eine Kopie der
Basisklasse beinhaltet Um vom abgeleiteten Typ wieder zum Ursrungstyp eines Objektes
zu gelanen, sieht der C + + tandard das sog. RTT runtime t e informatin) vor. Dies
wird j e d c h n c h kaum v pilern unterstützt
Im Normalfall werden nach einer automatischen Typanpassung die Methoden der Ba-
sisklasse benutzt, selbst wenn diese von der abgeleiteten Klasse überlagert wurden. Der
Grund dafür ist, daß so eine Codeoptimierung mit Method-Inlining5 öglich ist. Ist es für
die Krrektheit des Programms hingegen wichtig, daß ein late Binding geschieht, d.h. die
ü b e r l e r t e n Methoden der abgeleiteten Klasse benutzt werden, so kann dies für jede Me
thode esondert spezifiziert werden ( v i r t u a l Methoden). Für solche Methoden ist jedoch
oft ein Inlinin nicht möglich, s da ein Methodenaufru etwa den Aufwand eines Funkti
nsaufrufes in bedingt.
C + + weist somit Einschränkungen s o o h l hinsichlich des late Bindings wie auch beim
dynamic T y i n g auf Da beides nicht stren unterstützt wird, handelt es sich bei C + + auch
3
Es herrscht ein erbitterter Streit unter den Informatikern, ob die Pfeie in der oben beschriebenen
der in der umgekehrten Richtung zu zeichnen seien. Sowoh für als auch gegen beide Varianten sprechen
verschiedene uffassungen. Die hier verwendete Pfeirichtun entspricht der Bedeutun er er
ist ein" [45].
4
Dies gilt nicht für den Fall on virtual-Vererbung
5
Beim function-inlining wird anstelle eines Unterprogrammaufrufes der Funktionscoe direkt in den
aufrufenden C e k p i e r t . Dadurch entfällt der Beareitunsaufwand für die P a r a m e t e r ü e r e .](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-141-320.jpg)


![28 KAPITEL PLEMENTIERUNG IN C++
3.22. Dünnbesetzte V e k o r e n
Wie in Abschnitt 1.7 beschrieben, bedeutet die Dünnbesetztheit eines Vektrs, daß es sich
lohnt, nur die NNEs zu verwalten. Es gibt eine Vielzahl von Vorschlägen für geeignete
Darstellungen, die sich in der Effizienz für verschiedene Operationen unterscheiden [39]. In
Abschnitt 1.7.3.3 wurden verschiedene Speicherschemata für dünnbesetzte Matrizen vor-
gestellt und bewertet. Dieselben Überlegungen treffen auch für dünnbesetzte Vektren zu.
Deshalb verwaltet die Klasse SVector (Sparse Vector) die NNEs in einem Feld von Wert-
Index-Paaren Klasse SVector: :Element). Eine andere, wegen früherer Implementierun-
gen in FORTRAN oft eingesetzte Lösung, ist die getrennte Verwaltun der Indizes und
Werte in je einem Feld. ie wurde aus zwei Gründen nicht gewählt. Zum einen benötigte
das Verschicken eines SVectorObjektes in diesem Fall zwei Kommunikationen, während
bei der verwendeten Darstellung eine Kommunikation ausreicht. Zum anderen kann es
bei zwei Feldern leichter zu CacheMisses kommen, falls Indizes und Werte au dieselben
Cachelines abebildet werden.
Da NNE-Feld selbt wird nicht von SVector allo
ziiert. Stattdessen muß der zu verwendende Speicher
SVector
platz bei der Instantiierung eines SVector-Objektes
übergeben werden. Die Größe des Feldes bestimmt
SVector wieviele NNEs der SVector maximal aufnehmen
kann. Benötigt man einzelne dünnbesetzte Vektoren,
ist diese Instantiierung und Restriktion unnötig
UnitVector kompliziert. Deshalb wird mit DSVector eine weite-
Abbildung 3.2 re Klasse bereitestellt, die per Ableitung die Funk-
setzte Vektren tionalität vo SVectoren um eine dynamische Spei
cherverwaltung erweitert. DSVectoren stellen den NNE-Speicher intern zur Verfügung und
verwalten ihn dynamisch je nach Anforderung. Somit braucht von außen kein Speicher
bereitestellt zu werden, und es k n n e n hne eschränkunen NNEs hinzugefügt werden.
Benötigt man j e d c h eine ielzahl von dünnbesetzten Vektoren, so ist die Instanti-
ierung vieler DSVectoren nicht geeignet, da dabei viele Speicherblöcke alloziiert würden,
was eine hohen Ressourcenverbrauch bedingt. tattdessen kann eine Menge von SVectoren
einer gemeinsamen Speicherverwaltung unterworfen werden, die von der Klasse SVSet im-
lementiert wird. Die Details der interne Speicherverwaltung wurden bereits in Abschnitt
33 vgestellt
Als zweite von SVector abgeleitete Klasse implementiert UnitVector Einheitsvektoren
ie treten in SoPlex für die Darstellung von SchlupfVariablen oder einfache Schrankenun-
gleichungen auf. An dieser Stelle wird der Ableitunsmechanismus statt zur Erweiterung
einer Klasse zu ihrer Spezialisierung eingesetzt: Ein UnitVector ist ein SVector mit nur
einem NNE, das immer den Wert 1 hat. Alle mathematischen Operationen von dünnbe-
setzten Vektoren sind aber auch für Einheitsvektren sinnvll, was durch die Ableitungs
beziehun oftwaretechnisch ausedrückt wird.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-144-320.jpg)














![.1 TESTPROB
wei LPs zu rwarten s . Sie wurde weils mit echet u ezieht ich
uf die ptimale altenbas des skalierten LPs
ie tmenge der LPs besteht aus Problemen a der N e t b [ 7 ] d verschiedee
IB ehandelte P r o t e n [106]. Aus der Netl t m m e n die LPs 1 1 1 . Die meisten
urde die T t m e n g aufgnommen, wei von i h e n die Problembeispiel 220 abge-
eitet den. Dies j e d c h nicht f r „stocfor3" as LP mit de meiten Zeile
Salte us der Netlib, pilo ei n u m e c h bsonders schwieigs N e t P r o b l e m
fd" as das Problem mit de meite i c h t - l l E l e m e n t e n de Net
ie Probleme 20 mit de Endung ob d LP-Reaxieungen e i n s verallgemei
ten ckingProblems. Sie stamm a s dem Wuzelknoten e i s Branch-and-ut Verfh-
ns zur optimaln Dkomposition von Matizen in unabhängge Bl [19]. Sie enthalte
eits Schitte und haben meh Zei als Spalten. Die Name vor ,,.ob4" ezeich-
nen de Namen des NetlibProblem dess ptimale B a s i a t r i dekomponie de
soll; bei agg3ob4" also die ptimal B a s t von agg3"
eim Fequezzuweingsproblem im o b u n k geht arum Bassstation Fre-
quenzen so zuzuweien, aß sich möglicht g Intefeeze g b e wobei g s s e
technologche u echtiche n s c h ä n k n g n berücksichtigt de s s n . Die LPs
„ S M 6 8 " und „SM50k-68 d L P - R e a x i e u n g , die im Rahme e i e s Branch-
a n d - u t Verfahrens zur Lösung die Problem t e h e . Sie enthalte al Date de
obfnkAnbieters E P l s
it „ k a m i 8 0 u d „ k m i 2 7 0 wude wei LPs bezeichet, die e i e m P r o j e t zu
mmissonierung von Glückwunschkarte mmen. Sie thalte al Date von
dem K o o p e a t i o n s a r r Hrlitz G.
ei den Problemen „ c h c " „s handet es sich um L P - R e i e n g von
q u a t i c a s s g n m e t Problemen a de Q A L I B [ 3 ].
Das Problem „stolle" hat seinn Ursprung i der P l a n n g von N e t z r k Es ande
ich um ei Steinerbaumproblem mit Längenrtiktionen und osten uf de de
uch f die Problem t m m e die Daten a e i r r a l n A n d u n g .
em Projekt zur optimal Fazeugumufplanung tamme die LPs „anse-
u ansecoml" . Die beide Probleminstanzen etstehen bei der A f ü h r n g
ei column-gneration ns. Sie ethalten Date s r a l A n d u n g der Ham-
b r Hochban AG.
ie Ps 30-35 s m m e von e t a r t i t i o n n g Probleme etwa zur E n s a t z p a n n g von
C r w s bei groß F l u g n t e e h m e (aa = meican i r l s ) . Sie u d e n b e i t n [
utzt um die a r a l l i e n g de duale S i m p n s zu ten.
ie Auwah der LPs t etwas voreingenomme da als blich LPs mit meh
ei als S a l t e vorkommen. In dieem Fall sollte ich die V e r d u n g einer eilnbas
szahlen, was auch zu bobachte st. Der G r u d d f ü , aß „typische" LPs ehe mehr
alten als e i n aufwei t e d c h uch dar zu ehe bi d t o kei mplementie-](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-159-320.jpg)
![44 KA ERGEBNIS
g v e r g b a r ware die eine Zeinbasis nutze ute L P d e l l i e r hab he
eits bei der Mdellierung darauf g c h t e t daß die LPs mehr S a l t e als eilen h
notfalls duch den Übegang zu ei dual Formuierung. Duch f ü h n g de
einbasis n s a t e - f t h e - a r t Code i t es edoch wahrscheinlich aß z u f t i i
L P d e l l e e t e h e die meh Zei als S a l t e ab
Tablle A. nthält die ufzeite die An der Iterationen die C P E 07
die ösung der Tst-LPs b ö t i , d zwar so mit dem rimaln als auch mit dem
dualen Algorithmus. C P L X w d e weils mit de Voreinstellngen verendet. Da dies
I m p e m e t i e n g sicherlich als state-of-the-art a n g e h e de arf dient die T a b l l
als R e f z f die B t u n g von SoPlx.
ür ein ss gleichbarkeit seien nu Inforation ü X zusammenge-
faßt soweit die ö f f e i c h verfügbar snd [15, 16, 1 3 . All LPs erde vor ihre Lösung
skalie dem z u ä c h ede palte duch den größten ar u f t e t e d e Absolutbetrag
geteit und anschießend jede Zeie e t p e c h e n d behande wird C E X v e d e t
chließlich ein Spaltenbasis. Somit ist de dual Algorithmus stets ein n t f d e nd
der imal ein einfügender Als Pricingtrategie f r de dualen Algorithmus i das
teepet-ed Pricing e i n g e t z t wobei die initiale Norme icht exak bestimmt son
der uf etzt w d e n . Beim primaln Algorithmus kommt ein dynamiches Pricing
das wiche partial mutiple Pricing u eve Pricing umschaltet zum Ensatz Dabei
edoch keine w e i t e n I n f o r t i o n e n die D e t l s beider P r i c i n g a h n ode
der U c h a l t r a t e g i e ekann hase wird ein mpementierung de Composite
Simp e t h d e (vgl (1-9)) v e d e t . Die von SoPl benutzte Crashbasis de von
CPL eh hnlich [15]. Die sonders an den Tst-Problemen deutich, bei den
sow C P E als auch SoPle d i t mit Phase 2 b n n n könnn. Diese älle eign
ich sonders e i e vegleichede B e u t e i n g beide m p e m e t i e n g n .
4.2 oPlex
In de ersten Abschnitten 1 2 werden T u f e von SoPlex mit einer S a l t e
basis betrachtet um so eine ssere Vegleich mit PLEX zu ermöglichen. Da sich beide
Impemetieungn der Art der B e h a n u n g von P a s 1 unterscheide gl. Abschitt
1.4), wede z u c h s nu die Probleme e t c h t e t e t c h t e t ei de ufgr de
a r b a s s kei as 1 b ö t i d
ie ich a n s c h i e n d Abschnitte heben die sondeheiten von SoPle g
ande mpemetieng hevor. Als rste i t i diesem sammenang die ei
basis zu nn de utze n Abschitt 4 . 3 ertet . Anschließnd ird i
Abschitt 4.2 der Effekt der dynamische F a k o r i s i e u n g s q u e n z a u f e z e i . Der Vor
tei de Gleichungsstemlösrs r bsonders nnbetzte M t i z e d Abschitt
425 ufezeit
In de aruf f o l d e Abschitte de die rkng verschiede weite](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-160-320.jpg)




![4. OP
bei allen LPs. Ein besonders eklatantes Beispiel hierfür ist das Problem 3 (fit2d): Mit
steepestedge Pricing beötigt SoPlex für dessen ösung 5, s, mit partial multiple
Pricing lediglich s.
Insgesamt zeigen diese Ergebnisse Iterationen pro Sekunde beim primalen Simplex
und die des vorigen Abschnittes, daß 140
die Pricing-Strategie einen extremen II
Einfluß auf die Lösungsgeschwindigkeit 100
eines LPs hat. Dabei gibt es jedoch keine 80
allgemeine „optimale Pricing-Strategie. 60
^
Vielmehr sollte für ede Problemklasse 40 s-
L^
nach einer optimale Strategie gesucht
werden. Mit seinem objektorientierten
20
0
f
-<^i—'/ w /y / V
> 1
Alle LPs
1 Phase 2 LPs
s
Software-Entwurf bietet SoPlex hierfür
optimale Voraussetzungen.
enden wir uns nun den verbleiben- Abbildung 4.4: Durchschnittliche Iterationszahl pro
Sekunde beim primalen Simplex für CPLEX und So-
den LPs zu, bei denen auch ein Phase-1 Plex mit verschiedenen Pricing-Startegien.
Problem gelöst werden muß. Aus dem Ver-
gleich mit den Werten der Phase 2 LPs können Rückschlüsse auf den Unterschiede bei der
Phase zwischen CPLEX und SoPlex für den dualen Simplex gewonnen werden.
Die über alle TestBeispiele aufsummierten Iterationszahlen und Laufzeiten sind in der
zweiten Reihe von Abbildung 4.3 angegeben. Dabei wurde jedoch die Probleme 27 und
29 weggelassen, da CPLEX sie nicht in dem vorgegebenen Zeitrahmen von 3000 Sekun-
den lösen konnte. Auch sind die Werte für das Devex und most-violation Pricing lediglich
untere Schranken, da einige weitere LPs nicht innerhalb der Zeitbeschränkung gelöst wer
den konnten. Diese Probleme wurden jedoch nicht aus der Summenbildung ausgeschlossen,
um die Anzahl der Problembeispiele nicht noch weiter zu verringern. Eine aussagekräftige
Bewertung der ahlen ist auch so möglich.
Die wichtigste Beobachtung ist, daß sich das Verhältnis der Iterationszahle gegenüber
den Phase 2 LPs signifikant zugunsten von SoPlex verändert hat. Somit zahlt sich
aus, daß SoPlex bei seinem Phase-1 Problem soviel Information des AusgangsLPs bei
behält wie möglich. Insbesondere liegt bei einigen Problemen (Tabelle A.3, Probleme
2,21,22,23,2434) die Lösung des Ausgangs-LPs bereits vor, nachdem die Phase abge-
schlossen ist. CPLEX gelingt dies nur in einem Fall Tabelle A. Problem 24)
Durch die geringere Iterationszahl löst SoPlex mit steepestedge Pricing alle LPs in
deutlich kürzerer Zeit als CPLEX. Dabei wirkt sich zusätzlich die Tatsache positiv aus,
daß in der Phase 1 eine entfernender Simplex benutzt wird, bei dem das steepestedge
Pricing weniger Rechenaufwand benötigt als im einfügende Fall
Die Phase 1 von SoPlex scheint für den primalen Simplex also günstiger als eine Imple-
mentierung nach [100] Wieder ist dies keine beweisbare Aussage, sondern spiegelt lediglich
die Ergebnisse bei der gewählte Testmenge wider. Es wird immer Probleme geben, bei](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-165-320.jpg)

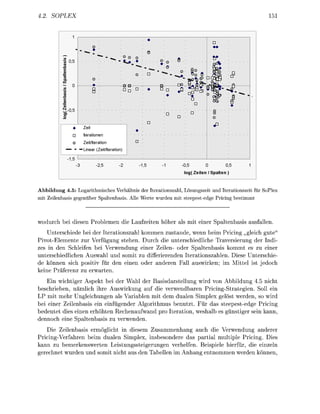
![KATEL 4. ERGEBNIS
nd (dualer Simplex mit Zeilenbasis
Problem steepest-edge artial multiple
0,5 s
03,0 08,3 s
530,83 s
7,
4.2.4 namische Refaktorisierung
Im Gegensatz zu 64] darf sich zur Bewertung des Erfolges der dynamischen Faktorisie-
rungsfrequenz der Vergleich nicht auf eine einzelne Faktorisierungsfrequenz beschränken,
sondern muß sich an dem „ p t i m u m für eine konstante Faktorisierungsfrequenz messen.
Dazu wurden die Zeiten pro 100 Iterationen für eine Reihe fester Faktorisierungsfrequenzen
zwischen 10 und 320 gemessen. Sie sind im einzelnen i Tabelle A. aufgeführt und die
Summen in Abbildung dargestellt.
Auch für die dynamische Faktorisierungsfrequenz wurde eine Testreihe über verschiede-
ne Werte von r§ zwischen 1 und 32 durchgeführt. Die ermittelten Iterationszeiten stehen in
Tabelle A . . Die mittleren Geschwindigkeiten wurden mit in Abbildung 4.6 aufgenommen,
obwohl die Werte r/cß nicht mit den statischen Faktorisierungsfrequenzen vergleichbar sind.
Dennoch bietet die gewählte Darstellung eine gute Gegenüberstellung beider Ansätze.
270
Für die statischen Faktorisierungsfre-
quenz ist ein eindeutiges Minimum der Zeit
—•—dynamisch
pro Iteration bei einer Faktorisierung der
D statisch Basismatrix alle 80 Iterationen festzustel
len. Bei seltenerer oder häufigerer Faktori
250
sierung sinkt die Iterationsgeschwindigkeit,
weil im ersten Fall der Rechenaufwand für
240 die Faktorisierung zunimmt und im zwei
ten Fall der Rechenaufwand für die Lösung
230 der Gleichungsssteme steigt.
10 20 40 80 160 320
1 2 4 16 32Dagegen zeigt die dynamische Einstel-
lung der Faktorisierungsfrequenz eine deut
Abbildung 4.6: Summe der Iterationsgeschwindig-
keit über alle Testprobleme für dynamische und sta- lich geringere Abhängigkeit von dem Ein-
tische Faktorisierungsfrequenz der BasisMatri nach stellparameter rj<p, sofern er größer als etwa
den Tabellen A.ll und A.12. 6 gewählt wird. Darunter kommt es zu ei
nem steilen Anstieg der Zeit pro Iteration, da die Basismatrix zu häufig faktorisiert wird.
Für rj<p > 6 ist die Iterationsgeschwindigkeit öher als die höchste mit fester Faktorisie-
rungsfreuenz erreichbare.
Schließlich wäre eine Heuristik denkbar, die vor Begin des Simplex-Algorithmus](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-168-320.jpg)

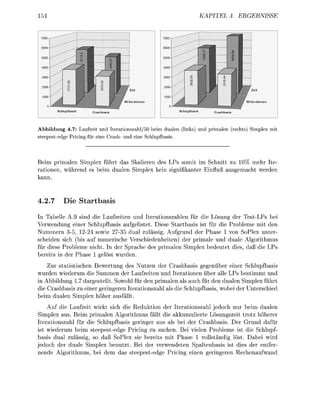

![KATEL 4. ERGEBNIS
Aufbrechen der Degeneriertheit lange PivotSequenzen ohne Forschritt entstehen. Das
ptimum liegt für die gegebene Testmenge bei etwa maxcycle = 16 Iterationen.
4.2. Der Quotientest
In den Tabellen A.13 und A.14 sind die TestErgebnisse von SoPlex bei Verwendung des
Quotiententests nach Harris bzw. des Textbook-Quotiententests verzeichnet. Dabei sind
die Ergebnisse im einzelnen von geringer Bedeutung. Vielmehr soll deutlich werden, daß i
beiden ällen nicht alle LPs gelöst werden konnten.
In den Fällen, die von beide Versionen mit gleicher Iterationszahl korrekt gelöst wer
den, stellt sich der Textbook-Quotiententest als der effizientere heraus. Dies ist aufgrund
des geringeren Rechenaufwandes im Vergleich zum zweiphasigen Harris Verfahren auch
zu erwarten. In diesem Zusammenhang ist die Beobachtung interessant, daß bei gleicher
Iterationszahl der Textbook-Quotiententest nur selten effizienter als der von SoPlex ist
(Ausnahmen bei den Problemen 11 und 23). Dies liegt am Weglassen von Phase , sofer
n Phase bereits ein stabiles PivotElement gefunden wurde.
Es ist jedoch zu bemerken, daß die drei Implementierungen des Quotiententests nicht
wirklich miteinander vergleichbar sind. Es ist zu erwarten, daß die Stabilität auch für
den Harris und den Textbook-Quotiententest durch eine dnamische Toleranzanpassung
und das Zurückweisen von PivotElementen (vgl. Abschnitt 1.8.2) weiter gesteigert werden
kann. Dergleichen wird vermutlich auch bei CPLEX vorgenommen, dessen Quotiententest
auf dem Ansatz von Harris basiert 5, 6]
4.3 SMoPl
Die in diesem Abschnitt vorgestellten Testergebnisse wurden auf einer SGI Challenge
mit 2 MIPS 4000 Prozessoren a 150 MHz durchgeführt. Die benutzte Maschine wird als
File-Server genutzt, so daß bessere Ergebnisse auf einem ausschließlich für SMoPlex zur
Verfügung stehenden Rechner zu erwarten sind. Ferner zeigt die Hardware Engpässe beim
Speicherbus: Die sequentielle ösung von nwlö beansprucht 1 2 9 . s , während die zwei
fache sequentielle Lösung von „nwl6 auf je einem Prozessor eweils 144.63s dauerte (user
time). Somit kann man für einen Parallelrechner, der keinen solchen Engpaß zeigt, eine
Verbesserung der Ergebnisse für Prozessoren um etwa erwarten.
Die Basisdarstellung wurde bei allen Testläufen so gewählt, daß die Dimension der
Basismatrix geringer ausfällt. Es wurde immer eine Schlupfbasis verwendet und der dua-
le Simplex-Algorithmus ausgeführt. Als Pricing-Strategie wurde das steepest-edge Pricing
verwendet, denn nur für dieses kann die parallele Lösung zweier Gleichungsssteme ver
wendet werden. Alle Zeiten wurden als wallclock time (real verstrichene Zeit gemessen.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-172-320.jpg)







![KATEL 4. ERGEBNIS
32 16 8 4 2
Anzahl Pes
Abbildung 4 . 1 : Beschleunigung in Abhängigkeit von der Anzahl von PEs für einige TestLPs.
gen dieses Abschnittes wurden von Michael G n s s vorgenommen.
4..1 Testatrizen
Die Dimensionen und Anzahlen der NNEs der Test-atrizen sind in den ersten Spalte
von Tabelle A . 0 aufgelistet. Die Matrizen stammen von zwei Quellen: Bei den Matri
zen SM-50a bis stocfor3 handelt es sich um die mit SoPlex bestimmten optimalen Spal
tenbasismatrizen der gleichnamigen LPs. Dabei wurden nur Matrizen höherer Dimension
ausgewählt. Sie dienen zur Beurteilung der Anwendbarkeit des parallelen Loseres für den
Simplex-Algorithmus.
Die restlichen Matrizen kommen aus dem HarwellBoeing Testset [0]. Er ist fast schon
ein Standard bei der Evaluierung von Gleichungssystemlösern und ermöglicht somit einen
Vergleich mit anderen Implementierungen. Hierbei ist vor allem die i 5] vorgestellte Im-
plementierung für den T3D interessant.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-180-320.jpg)

![66 KATEL 4. ERGEBNIS
zen. Dies gilt umso mehr, als optimale BasisMatrizen in der Regel die dichtbesetzteste
Matrizen während der Ausführung des Simplex-Algorithmus' sind. Gleichungssysteme mit
zwischenzeitlichen Basen werden somit meist mit weniger Aufwand gelöst, was de Nutzen
von Parallelität für den Simplex-Algorithmus weiter einschränkt.
Liegt das unerfreuliche Ergebnis für die parallele Lösung von BasisMatrizen vielleicht
an einer schlechten Implementierung? Die Antwort ist Nein, was anhand der Testmatrizen
aus dem HarwellBoeing Testset im Vergleich zu anderen publizierten Ergebnissen auch
nachgeweisen werden kann. R. Asenjo und E.L. Zapata berichten in [5] folgende aufzeite
ihres FaktorisierungsAlgorithmus auf einem Cr T3D
Problem Es Es
steam 989 3. 1.
jpwh9 16.22 3.
sherman 3.02 1 1.3
sherman 08 228 8.
ns337 8 8.
Lediglich bei „sherman2 und 1 PEs überholt die Implementierung von R. Asen
und E.L. Zapata die hier vorgestellte Version. In allen anderen Fällen sind die Laufzeiten
mitunter erheblich höher. Zwar ist ihre Effizienz nach (23) besser, jedoch ist die Bedeutung
dieser Maßzahl angesichts der absoluten Laufzeiten i age zu stellen.
Insgesamt ist somit festzustellen, daß die im Rahmen dieser Arbeit erstellte parallele
Implementierung vergleichsweise günstige Laufzeiten erreicht und somit nicht für den Miß-
erfolg bei den LP BasisMatrizen verantwortlich gemacht werden kann. Die Skalierbarkeit
der Implementierung steigt mit zunehmender Arbeit, was sie für den Einsatz in anderen
Anwendungsfeldern interessant macht. Der Einsatz für die ösung partieller Differential
gleichung ist geplant.
Als besonders interessantes Phänomen ist in Tabelle A.20 eine superlineare Beschleuni
gung für „lns2927" bei 2 PEs zu erkennen. Dies ist darauf zurückzuführen, daß der parallele
Algorithmus für unterschiedliche Anzahlen von PEs meist unterschiedlich viel Arbeit lei
stet. Je mehr PEs eingesetzt werden desto größer wird die Menge der PivotKandidaten,
was jeweils zu einer anderen Eliminationsfolge führt. Durch die größere Kandidatenmenge
können zweierelei Effekte eintreten. Zum einen können so PivotElemente mit geringerer
Markowitz-Zahl gefunden werden, was zu einer Verringerung der Gesamtarbeit führt und
die superlineare Beschleunigung für ns erklärt.
Leider kann zum anderen auch der gegenteilige Effekt eintreten, was leider häufiger
geschieht. In die größere Kanidatenmenge werden mangels Alternativen auch NNEs mit
höherer Markowitz-Zahl aufgenommen. Fallen diese Kandidaten nicht durch den Kompati
bilitätscheck, führen sie zu Eliminationsschritten, bei denen viel Fill erzeugt wird. Dadurch
erhöht sich die Gesamtarbeit. Beim Problem „sherman3 zeigt sich dieser Effekt so deut
lich, daß die Laufzeit für 2 PEs die für 1 PE sogar übertrifft. Hier könnte eine Begrenzung
der maximalen arkowitz-ahl weiterhelfen.](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-182-320.jpg)




![an
Tabelle
Dieser Anhang enthält alle MeßwertTabellen, die für die Bewertung der Implementierun-
gen SoPlex, SMoPlex und DoPlex sowie für den parallelen Löser für dünnbesetzte lineare
Gleichungssysteme erstellt wurden. Ihre Auswertung und ggfs. graphische Aufbereitung
ndet sich in Kapitel
Die Ergebnisse zu SoPlex und CPLEX wurden auf einer Sun UltraSPAR 1 Model
170E gemessen, die zu SMoPlex auf einer SGI Challange mit zwei 150MHz MIPS 00
Prozessoren. Die Werte für DoPlex sowie für die parallele LU-Zerlegung und Lösung ünn-
besetzter linearer Gleichungssysteme wurden auf einem Cray T3D gemessen. Jede PE hat
MB Speicher und einen 15 MHz DE alpha Prozessor ohne 2nd level cache.
Bei allen Simplex-Testläufen wurde die maximale Berechnungszeit auf 3000 Sekunden
beschränkt, auf dem Parallelrechner Cray T3D (aus administrativen Gründen sogar auf
1800s. Konnte ein LP in dieser Zeit nicht gelöst werden, so wird dies durch „>" angezeigt.
Konnte ein LP hingegen aufgrund anderer Probleme, insbesondere aufgrund der numeri
schen Stabilität, nicht gelöst werden, so wird dies durch gekennzeichnet. Auf dem
T3D wurde ausgehend von 1 PE ein LP nur dann mit mehr PEs gelöst, wenn eine weitere
Beschleunigung erwartet werden konnte.
Bei den Meßergebnissen zu SoPlex wurden folgende Einstellungen verwendet
steepestedge Pricing
SoPlex Quotiententest
Spaltenbasis
skaliertes LP
Crashbasis
maxcycle = 100 ( g l . Abschnitt
T]9 = 10 (vgl. Abschnitt 8.
• S l e - 6 vgl. Abschnitt 3](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-187-320.jpg)
![ANHANG A. T
Nur die Abweichungen davon werden bei den Tabellen aufgeführt. ür die Mesungen zu
SMoPlex und DoPlex wurden folgende Einstellungen verwendet
steepestedge Pricing
SoPlex Quotiententest
Basisdarstellung jeweils so, daß die Dimension niedriger ausfällt
unskaliertes LP
Schlupfbasis
maxcycle = 100 gl. Abschnitt
7]9 = 10 (vgl. Abschnitt 8.
-6
• S le vgl. Abschnitt 3](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-188-320.jpg)


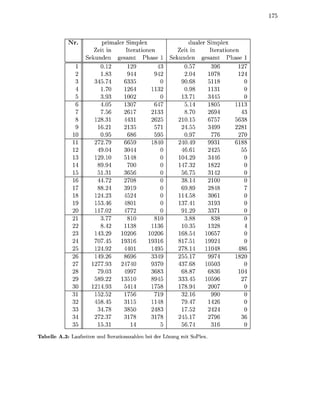
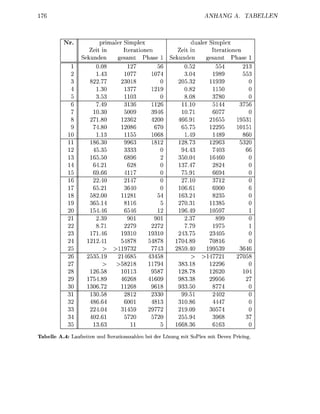
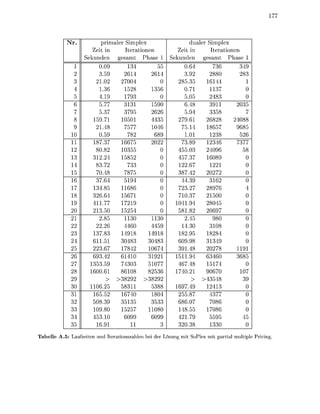


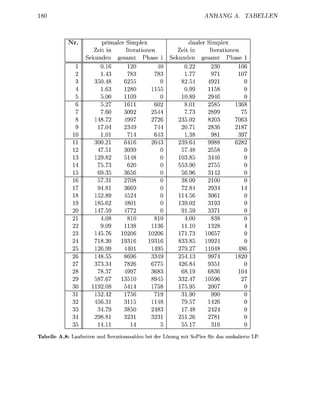
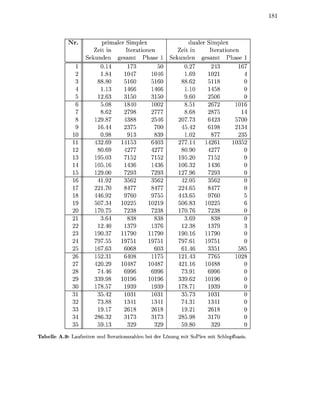
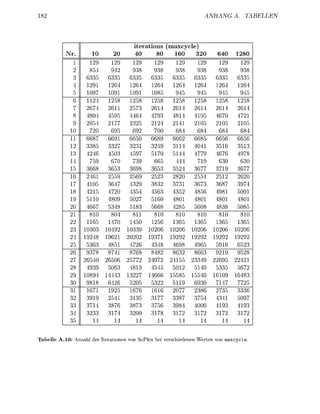

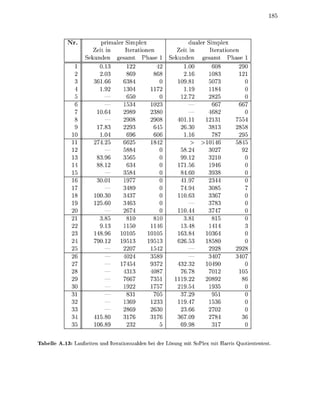
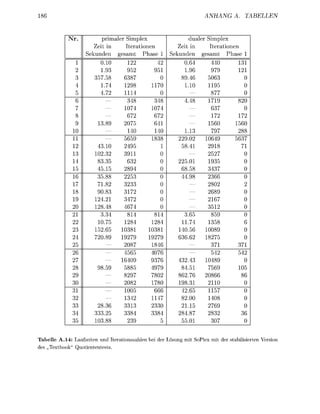
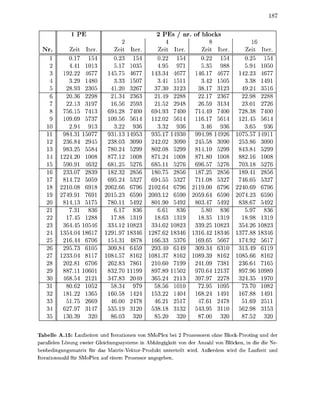



![iteratrverzeic
1] G.M. AMDAHL, Validity of the single-processor approach to achieving largescale
computing capabilities, AFIPS Conference Proceedings, 30 (1967, pp. 83-
] N. AMENTA AND G.M. ZIEGLER, Deformed products and maximal shadows of
polytopes, TU Berlin Preprint Reihe Mathematik, Report No. 502/1996
] E.D. ANDERSEN AND K.D. ANDERSEN, Presolving in linear programming
Math. Prog. 71 (1995), pp. 221245
] K.M. ANSTREICHER AND T. TERLAKY A monotonic build-up simplex algorithm
for linear programming Op. Res. , 42, 3 (1991), pp. 55656
5] R. ASENJO AND E.L. ZAPATA, Sparse LU factorization on the Cray T3D, Lec
ture Notes in Computer Science 919 (1995), pp. 90, Springer Verlag
6] O. AXELSSON, A survey of preconditioned iterative methods for linear systems of
algebraic equations, BIT 25 (1985), pp. 166187
7] D.A. BABAYEV AND S.S. MARDANOV, Reducing the number of variables in
integer and linear programming problems Comp. Opt Appl. 3 (1994) pp. 10
8] M.A. BADDOURAH AND D.T. NGUYEN, Parallelvector processing for linear
programming Computers & Structures No. 38, Vol. 3 (191), pp. 69281
9] R.S. B A R R AND B.L. HICKMAN, Parallel simplex for large pure network pro-
blems: Computational testing and sources of speedup, Op. Res 42, 1 (1994) pp. 6
80
10] R.H. BARTELS AND G.H. GOLUB, The simplex method of linear programming
using LU decomposition, Comm. ACM 12 (1969), pp. 266268
11] R.K. BARYTON, F.G. GUSTAVSON, AND R.A. WILLOUGHBY, Some results on
sparse matrices Math. Comp. 24 122 (1970), pp. 937954
] M. BENICHOU, J.M. GAUTHIER, G. HENTGES AND G. RIBIERI, The effi-
cient solution of largescale linear programming problems, Math. Prog. 13 (1977)
pp. 28032](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-210-320.jpg)

![96 LITERURVERZEIC
8] A.R. CURTIS AND J.K. R E I D , On the automatic scaling of matrices for Gaussian
elimination, J.o.tInst. of Math. a.i. Appl 10 ( 1 9 7 , pp. 118
9] G.B. DANTZIG AND W. ORCHARD-HAYS, The product form for the inverse in
the simplex method Math. Comp. 8 (1954), pp. 6467
0] G.B. DANTZIG, A. ORDEN AND P. W O L F E , The generalized simplex method
for minimizing a linear form under linear inequality retraints, Pacific Journal of
athematics 5 (1955), pp. 183-195
1] G.B. DANTZIG AND P. W O L F E , Decomposition principle for linear programs
Op. Res 8 (1960), pp. 101111
32] G.B. DANTZIG, Linear programming, in „Histroy of Mathematical Program-
ming", J.K. Lenstra, A.H.G. Rinnooy Kan and A. Schrijver eds, North-Holland
Amsterdam, 1991
33] T.A. DAVIS AND P. Y E W , A nondeterministic parallel algorithm for general
unsymmetric sparse LU factorization, SIAM J. Matrix Anal. Appl 11, 3 (1990)
pp. 383-4
4] P. DEUFLHARD AND A. HOHMANN, Numerische Mathematik I de Gruyter
(1993)
5] E . . DlJKSTRA, GO TO statement considered harmful, CACM V, 11 No. 3
6] E.W. DlJKSTRA, Structured programming, Nato Science Comittee - Software
Engineering Techniques (1970)
7] A. DONESCU, The simplex algorithm with the aid of the Gauss-Seidel method
Econ. Comput and Econ. Cybernetics Studies and Research, 4 (1989) pp. 12
132
8] LS. D U F F AND J.K. R E I D , The multifrontal solution of unsymmetric sets of
linear equations, SIAM J. Sei. Stat. Comp. 5 (1984), pp. 633-641
9] LS. D U F F , A.M. ERISMAN AN J.K. REID Direct Methods for Sparse Matrices
Clarendon Press, Oxford (1986)
0] LS. D U F F , R.G. GRIMES, AND J.G. LEWIS, Sparse matrix test problems AC
Trans Math. Soft 15 1 (1989), pp. 114
41] LS. D U F F , Parallel implementation of multifrontal schemes Parallel Computing,
3 (1986), pp. 193-04
] S.K. ELDERSVELD AND M.A. SAUNDERS, A block-LU update for largescale
linear programming, SIAM J. Matrix Anal. Appl 2, 1 (1992), pp. 1 9 1 0 1](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-212-320.jpg)

![LITERURVERZEIC
58] J.A.J. HALL AND K.I.M. M C KINNON An asynchronous parallel revised simplex
algorithm, Department of Math, and Stat. University of Edinburgh, MS 95050
(1995)
59] J.A.J. HALL AND K.I.M. Mc KINNON, PARSMI, a parallel revised simplex
algorithm incorporating minor iterations and Devex pricing, PARA96: Workshop
on Applied Parallel Computing in Industrial Problems and Optimization Copen-
hagen (1996)
60] P.M.J. HARRIS, Pivot selection methods for the Devex LP code, Math. Prog.
(1973), pp. 128
61] M. HEATH, E. N G , AND B. PEYTON, Parallel algorithms for sparse linear sy-
stems, SIAM J. Comp. 21 1 (1991), pp. 1 1 1 9
] R.V. HELGASON AND J.L. KENNINGTON, A parallelization of the simplex me
thod, An. Op. Res 14 (1988), pp. 1740
] E. HELLERMAN AND D. RARICK, Reinversion with the preassigned pivot proce
dure Math. Prog. 1 2 (1971), pp. 195215
64] J.K. Ho AND R.P. SUNDARRAJ, A timing model for the revised simplex method
Op. Res. Letters 13 (1993), pp. 677
65] A.J. HOFFMAN, Linear programming at the National Bureau of Standards, in
„History of Mathematical Programming", J.K. Lenstra, A.H.G. Rinnooy Kan
and A. Schrijver eds, North-Holland Amsterdam, 1991
66] M.T. JONES AND P.E. PLASSMANN, Scalable iterative solution of sparse linear
systems, Par. Comp. 20 (1994), pp. 753-77
67] N.K. KARMARKAR, A new polynomialtime algorithm for linear programming
Combinatorica, 4 (1984), pp. 33-395
68] M. KATEVENIS, RISC Architectures, in „Parallel & Distributed Computing
Handbook", A.Y. Zomaya ed. McGrawHill (1996)
69] L.G. KHACHIAN, A polynomial algorithm in linear programming, Soviet
Math. Doklady 20 (1979), pp. 191194
70] V. K L E E AND P. KLEINSCHMIDT The d-step conjecture and its relatives Math, of
Op. Res 12, 4 (1987), pp. 718755
71] H.W. KUHN AND R.E. QUANDT, An experimental study of the simplex method
Proceedings of Symposia in Applied Mathematics 15 (1963), pp. 107124](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-214-320.jpg)
![LITERURVERZEIC 199
] E.V. KRISHNAMURTHY, Complexity issues in parallel and distributed computing
in „Parallel &: Distributed Computing Handbook, A.Y. Zomaya ed., McGraw
Hill (1996)
] D.W. KRUMME Fast gossiping for the hypercube SIAM J. Comput (199
pp. 365380
74] A. LÖBEL, Optimal vehicle scheduling in public transit, PhD thesis, Technical
University of Berlin, in preparation
75] J. Luo, A.N.M. HULSBOSCH AND G.L. R E I J N S , An MIMD work-station for
large LP problems, Par. Proc and Appl, Proc. Int. Conf. , L'Aquila (1987)
76] I.J. LUSTIG, R.E. MARSTEN AND D.F. SHANNO, Interior point methods for
linear programming: computational state of the art, ORSA J. Comp. 6 1 (1994)
pp. 114
77] H.M. MARKOWITZ, The elimination form of the inverse and its application to
linear programming, Management Sei. 3 (1957), pp. 255269
78] K. MARGARITIS AND D.J. EVANS, Parallel systolic LU factorization for simplex
updates, in „Lecture Notes in Computer Science G. Goos an J. artmanis eds
Springer Verlag 1988
79] I. NASSI AND B. SCHNEIDERMAN Flowchart techniques for structured program-
ming, SIGPLAN Notices (1973)
80] M. PADBERG, Linear Programming and Extensions, Algorithms an Combina-
torics, Vol 12. Springer Verlag (1995)
81] M. PADBERG AND M.P. RIJAL, Location, Scheduling Design and Integer Pro-
gramming Kluwers's International Series (1996)
] P . Q . PAN, A Simplex-like method with bisection for linear programming, Opti
mization, 22 (1991), pp. 717743
] D.A. R E E D AND M.L. PATRICK, Parallel iterative solution of sparse linear sy-
stems: Models and architectures, Par. Comp. (1985), pp. 4567
84] J.K. R E I D , A sparsity-exploiting variant of the BartelsGolub decomposition for
linear programming bases, Math. Prog. 24 (1982), pp. 5569
85] P. SADAYAPPAN AND S.K. R A O , Communication reduction for distributed sparse
matrix factorization on a processor mesh, Supercomputing '89, AC Press New
York (1989), pp. 371379](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-215-320.jpg)

![LITERURVERZEIC 01
101] R. WUNDERLING, H.C. H E G E , AND M. GRAMMEL, On the impact of commu-
nication latencies on distributed sparse LU factorization, ZIB Preprint SC 93-28
(199
1 0 ] M. YANNAKAKIS, Computing the minimum fillin is NP-complete SIAM
J. Alg. Disc Meth. 1 (1981), pp. 7779
1 0 ] S. ZHANG, On anticycling pivoting rules for the simplex method Op. Res Letters
10 (1991), pp. 189192
104] G.M. Z I E G L E , Lectures on Polytopes, Graduate Texts in Mathematics 152,
Springer Verlag (1995)
105] X. ZHU, S. ZHANG AND A.G. CONSTANTINIDES, Lagrange neural networks for
linear programming, J. Par. Distr. Compt 14 (1992), pp. 354360
106] ZIB Jahresbericht 1995
107] anonymous ftp: r e s e a c h . a t t com:/dist/lpdata](https://image.slidesharecdn.com/soplex-tr-100422010730-phpapp02/85/Soplex-tr-217-320.jpg)



