Das Dokument behandelt die grundlegenden Konzepte der Thermodynamik und Physikalischen Chemie, einschließlich der Klassifizierung von Systemen, Phasen, Zustandsgrößen, und den Hauptsätzen der Thermodynamik. Es erklärt die Eigenschaften idealer und realer Gase sowie deren Zustandsänderungen und umfasst auch die mathematischen Beziehungen zur Beschreibung dieser Prozesse. Zusätzliche Themen sind chemische Gleichgewichte, elektrochemische Prozesse und verschiedene thermodynamische Potentiale.





![Physikalische Chemie
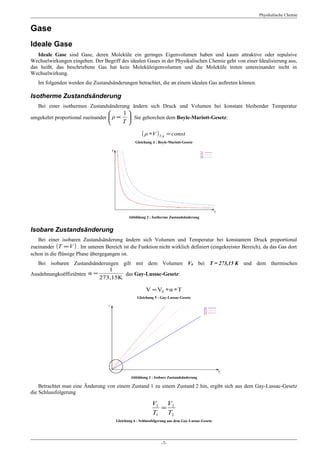
Zustandsgleichung eines idealen Gases
Ein ideales Gas kann durch die Zustandsgleichung eines idealen Gases beschrieben werden:
ρ ∗V = n ∗ R ∗T
Gleichung 11 : Zustandsgleichung idealer Gase 1
Die Größe R ist die allgemeine Gaskonstante. Sie leitet sich aus dem Produkt der Bolzmann-Konstante kB1 und der
Avogadro-Konstanten NA her:
J −2 bar ∗ l
R = k B ∗ Ν A = 8,3145 = 8,3142 ∗10 mol ∗ K
mol ∗ K
Gleichung 12 : Allgemeine Gaskonstante
Die Einheitenrechnung für Gl. 12 ergibt sich durch Umformung in SI-Einheiten und zurück:
J Nm
N
∗ m3 N
∗10 3 ∗ dm 3 10 −5 bar ∗103 l 10 −2 bar ∗ l
[ R] = = = m2
= m2
= =
mol ∗ K mol ∗ K mol ∗ K mol ∗ K mol ∗ K mol ∗ K
Gleichung 13 : Einheitenrechnung für die allgemeine Gaskonstante
Gelegentlich findet sich für die Gl. 12 auch die Schreibweise
ρ ∗ν = R ∗T
Gleichung 14 : Zustandsgleichung idealer Gase 2
V
Die Variable ν bezeichnet nichts weiter als das molare Volumen, das heißt ν =
η
.
Reale Gase
Bei realen Gasen werden intermolekulare Anziehungskräfte und das Volumen der Teilchen berücksichtigt.
Abbildung 7 : Zustandsdiagramm realer Gase
Ideales Gas: (p*V)=const., d.h. parallel zur ρ-Achse
Reales Gas: (p*V)≠const.
Korrekturen der idealen Gasgleichung führen zu der Van der Waalschen-Gleichung:
a
ρ + 2 ∗ ( ν − b) = R ∗ T
ν
Gleichung 15 : Van der Waals-Gleichung
mit a und b als Van der Waals-Konstanten und ν als molarem Volumen.
Die Isothermen des CO2 bei verschiedenen Temperaturen zeigen sich somit unstetig:
Abbildung 8 : Isotherme des CO2
1 −23 −1
k = 1,38 ∗10 J ∗K
Β
-9-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-7-320.jpg)


![Physikalische Chemie
Überführung eines idealen Gases von T1 → T2
Abbildung 9 : Überführung eines idealen Gases von T1 / T2
Chemische Reaktionen
Am Beispiel der einfachen Reaktion von Zink mit Chlorwasserstoff in einem geschlossenen System sei hergeleitet, ob
eine Reaktion unter Energieaufnahme oder Energieabgabe reagiert.
Zn ( s ) + 2HCl ( l ) → ZnCl 2 + H 2 ( g )
Formel 1 : Umsetzung von Zink mit Salzsäure
Stellen wir die Gleichung für die Reaktionsenergie auf, die ja aus der Differenz zwischen der inneren Energie am
Anfang und am Ende ist und greifen dabei direkt auf die Definition der inneren Energie durch den ersten Hauptsatz (siehe
Gl. 24) zurück, ergibt sich
ΔU R = U E − U A = ΔQ R − ρ ∗ ( VE − VA )
Gleichung 25 : Gleichung für die Reaktionsenergie
Wie oben angegeben ist die Reaktion isochor/isotherm: ((δV = 0) -ρ*(VE - VA) =0). Die Reaktionsenergie entspricht
damit der Reaktionswärme ΔQR = δQ2 - δQ1.
Führen wir die gleiche Reaktion unter isobar/isothermen Bedingungen durch, ergibt sich als Reaktionswärme aus der
Gl. 25 eine Größe, die wir als Reaktionsenthalpie ΔHR bezeichnen:
ΔH R = ΔU R + ρVR
Wir bezeichnen eine Reaktion als
● exotherm, wenn ΔHR<0 und als
● endotherm, wenn ΔHR>0.
Anschaulich gesprochen: Eine exotherme Reaktion gibt Wärme an die Umgebung ab, eine endotherme Reaktion
benötigt Wärme aus der Umgebung, das heißt, kühlt die Umgebung ab.
Um mit Reaktionsenthalpien besser rechnen zu können, normiert man sie wie folgt:
● Die molare Standardreaktionsenthalpie ΔH0m,R ist die Reaktionsenthalpie bei Standardbedingungen
(ρ = 1013 hPa, T = 298 K), bezogen auf 1 Mol Umsatz.
● Die molare Standardbildungsenthalpie ΔH0m,B ist der auf 1 Mol und Standardbedingungen bezogene
Wärmeaustausch bei der Bildung eines Stoffes aus seinen Elementen. Elemente selbst haben ΔH0m,B = 0 kJ*mol-
1
.
Die Wegunabhängigkeit der Reaktionsenthalpie
Der Satz von Hess besagt: Die Reaktionsenthalpie eines chemischen Gesamtvorgangs wird durch den Anfangs- und
den Endzustand eindeutig bestimmt. Das Ergebnis der Enthalpiebilanz ist unabhängig vom Weg und von der Anzahl der
Zwischenstufen, auf denen beziehungsweise über die der Endzustand erreicht wurde.
Wie geht man nun zur Bestimmung der Reaktionsenthalpie vor?
1.Man stellt die Reaktionsgleichung so auf, dass die interessierende Komponente den stöchiometrischen Faktor 1 erhält.
2.Man bildet die Summen der mit den Stöchiometriefaktoren multiplizierten molaren Bildungsenthalpie aller Produkte
und zieht die entsprechende Summe für die Edukte ab.
Beispiel: Ethin verbrennt gemäß der Formel
5
C 2H2 [ g] + O 2 [ g ] → 2CO 2 [ g ] + H2 O [ l]
2
Formel 2 : Verbrennung von Ethin
-12-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-10-320.jpg)

![Physikalische Chemie
Die Entropie von HCl als Funktion der Temperatur verläuft stufenweise:
Abbildung 10 : Entropie von HCl als Funktion der Temperatur
Warum gefriert eine Substanz, wenn diese Zustandsänderung mit einer Entropieabnahme verbunden ist?
Zustandsänderungen verlaufen nicht unabhängig von ihrer Umgebung:
dS Ges = dSSys + dS Umg
Gleichung 31 : Abhängigkeitender Zustandsänderung
Beim Gefrieren wird Schmelzenthalpie freigesetzt und von der Umgebung aufgenommen. Diese Energie vermehrt die
Entropie der Umgebung. Wenn die Entropiezunahme in der Umgebung größer ist als die Entropieabnahme der gefrierenden
Flüssigkeit, erfolgt das Gefrieren freiwillig.
Beispiel: Für Wasser ↔ Eis bei 101,3 kPa gelten:
dSSys[J*K-1*mol- dSUmg[J*K-1*mol- dSGes[J*K-1*mol-
T[°C] 1 1 1
] ] ]
+1 -22,13 +22,05 -0,08
0 -21,99 +21,99 0
-1 -21,85 +21,93 +0,08
Tabelle 6 : Entropieänderung des Systems Wasser ↔ Eis
Bei chemischen Reaktionen berechnet man die molare Standardreaktionsentropie ΔS0m,R aus tabellierten molaren
Standardentropien der Produkte und Edukte (Analogie zum Satz von Hess):
2H 2 ( g ) + O 2 ( g ) → 2H 2 O( g )
0 0
[
ΔS m,R = 2 ∗ S m ( H 2 O,g ) − 2 ∗ S m ( H 2 ,g ) + 1 ∗ S m ( O2 ,g )
0 0
]
J J
ΔS m,R = [ ( 2 ∗ +189 ) − ( 2 ∗ +131) + (1 ∗ +205) ]
0
= −89 K ∗ mol
K ∗ mol
Gleichung 32 : Berechnung der molaren Standardreaktionsentropie für die Bildung von Wasser aus den Elementen
Stehen negative ΔS0m,R in Widerspruch zum Zweiten Hauptsatz?
Auch hierbei muss die Umgebung mit einbezogen werden, bei obiger Reaktion beträgt die molare
Standardreaktionsenthalpie
kJ
ΔH 0 R = 2 ∗ ΔH 0 B ( H 2 O, g ) = −484
m, m,
mol
Gleichung 33 : Molare Standardenthalpie der Bildung von Wasser aus den Elementen
Sie entspricht der auf die Umgebung übertragenen Wärme dQ=-ΔH0m,R und führt zu einer Entropieänderung in der
Umgebung:
dQ 484kJ kJ
dSUmg = = = 1624
T 297 K ∗ mol mol
Gleichung 34 : Entropieänderung der Umgebung bei der Bildung von Wasser aus den Elementen
Die Entropieänderung des gesamten abgeschlossenen Systems ist in Übereinstimmung mit dem Zweiten Hauptsatz
größer Null:
J
dSGes = dSSys + dS Umg = [ − 89 + 1.624] >0
K * mol
Gleichung 35 : Entropieänderung des gesamten abgeschlossenen Systems
-14-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-12-320.jpg)


![Physikalische Chemie
Die freie Reaktionsenthalpie als Funktion von Reaktionsenthalpie, Reaktionsentropie
und Temperatur
Fall 1: ΔHR<0, ΔSR>0 Fall 2: ΔHR<0, ΔSR<0
Bei allen T exergonisch T2>T1: bei T1 exergonisch, bei T2 endergonisch
Fall 3: ΔHR>0, ΔSR>0 Fall 4: ΔHR>0, ΔSR<0
T2>T1: bei T1 endergonisch, bei T2 exergonisch Bei allen T endergonisch
Tabelle 7 : Die freie Reaktionsenthalpie als Funktion von Reaktionsenthalpie, Reaktionsentropie und Temperatur
Berechnung molarer freier Standardreaktionsenthalpien
Die Berechnung molarer freier Standardreaktionsenthalpien verläuft unter Anwendung der Gibbs-Helmholtz-Gleichung
40 aus molaren Standardreaktionsenthalpien ΔH0m,R und molaren Standardreaktionsentropien ΔS0m,R. Nach dem Satz von
Hess und in Analogie zur Berechnung einer Reaktionsenthalpie beziehungsweise Reaktionsentropie verwendet man
tabellierte Werte molarer freier Standardbildungsenthalpien ΔG0m,B.
Beispiel: Die Synthese von Salpetersäure aus Stickstoffdioxid, Wasser und Sauerstoff.
4NO 2 ( g ) + 2H 2 O( l ) + O 2 ( g ) → 4HNO 3 ( l )
ΔG 0
m,R = 4 ∗ ΔG 0
m,B ( HNO3 ( l ) ) − [4 ∗ ΔGm,B ( NO2 ( g ) ) + 2 ∗ ΔGm,B ( H 2O( l ) ) + 1∗ ΔGm,B ( O2 ( g ) ) ]
0 0 0
kJ kJ kJ kJ kJ
ΔGm,R = 4 ∗ -81
0
− 4 ∗ 51 + 2 ∗ -237 +1∗ 0 = −54
mol mol mol mol mol
Gleichung 44 : Synthese von Salpetersäure aus Stickstoffdioxid, Wasser und Sauerstoff
Temperatur- und Druckabhängigkeit der freien Enthalpie
Aus der Definition der Änderung der inneren Energie (siehe Gl. 19), der Gibbs-Helmholtz-Gleichung (siehe Gl. 40) und
der Volumenarbeit (siehe Gl. 23) können wir nun die Funktion der inneren Energie besser verstehen:
dU = TdS − ρdV
Gleichung 45 : Innere Energie 1
U ist damit eine Funktion der Entropie und des Volumens: U = U(S,V).
Die Enthalpie H = U + ρ*V lässt sich differenziell nach dU umstellen, man erhält dU = dH – ρ * dV-V. Setzt man diese
Gleichung gleich der Gl. 45 und stellt um, erhält man
dH = TdS +Vdρ
Gleichung 46 : Innere Energie 2
H ist damit eine Funktion der Entropie und des Drucks: H = H(S,ρ).
Setzen wir wieder die Gibbs-Helmholtz-Gleichung in differenzieller Schreibweise, erhalten wir
dG = −SdT +Vdρ
Gleichung 47 : Innere Energie 3
ist somit eine Funktion der Temperatur und des Drucks: =(T,ρ).
Damit ergeben sich
δG
● die Temperaturabhängigkeit: = −S und
δT p
δG
● die Druckabhängigkeit:
δρ T =V .
-18-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-15-320.jpg)





![Physikalische Chemie
Beispiel: Sauerstoff bei 25 °C und ρ = 0,2 bar
0 ,2[bar ∗ K ∗ mol ] mol
c= = 8,1 ∗10 −3
8,134 ∗ 298[ bar ∗l ∗ K ] l
mol
k H = 1,25 ∗10 −3
l ∗bar
mol ∗bar mol
cO2 ( Blut ) = 1,25 ∗10 −3 ∗ 0 ,2 = 2 ,5 ∗10 −4
l ∗bar l
Gleichung 75 : Sauerstofflöslichkeit in Blut
Kolligative Eigenschaften
Kolligative Eigenschaften hängen nur von der Anzahl der gelösten Teilchen und nicht von ihrer chemischen Natur ab:
● Dampfdruckerniedrigung
● Siedepunktserhöhung
● Gefrierpunktserniedrigung
● Osmotischer Druck
Bei binären Mischungen mit nur einer flüchtigen Komponente wird der Dampfdruck einer Komponente vernachlässigt.
Es werden ideal verdünnte Lösungen angenommen. Folgende Konvention wird verwendet:
● Index „1“ = Lösungsmittel (LM)
● Index „2“ = Gelöster Stoff (G)
Dampfdruckerniedrigung
Über einer Lösung befindet sich im Gasraum Dampf des Lösungsmittels. Nun gilt für einen reinen Stoff(*):
ρ*
μ(*l ) = μ*g ) = μ(0g ) = R ∗T ∗ ln
(
ρ0
Gleichung 76 :
Analog gilt für die Komponente Lösungsmittel der Lösung:
ρ1
μ1( l ) = μ1( g ) = μ10( g ) + R ∗ T ∗ ln
ρ0
*
ρ1 ρ
μ1( l ) = μ1( l ) + R ∗ T ∗ ln
*
+ R ∗ T ∗ ln 1
ρ0 ρ0
ρ1
μ1( l ) = μ1( l ) + R ∗ T ∗ ln
*
*
ρ1
μ1( l ) = μ1( l ) + R ∗ T ∗ ln χ1
*
Gleichung 77 :
Aus den vorangegangenen Überlegung ergibt sich nun das Raoultsche Gesetz:
ρ1 = ρ1 ∗ χ1
*
Gleichung 78 : Raoultsches Gesetz
Der Dampfdruck der Lösung einer nichtflüchtigen Substanz ist gleich dem Produkt aus dem Dampfdruck des reinen
Lösungsmittels und seinem Stoffmengenanteil.
Abbildung 15 : Diagramm einer Lösung einer nichtflüchtigen Substanz
-25-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-21-320.jpg)

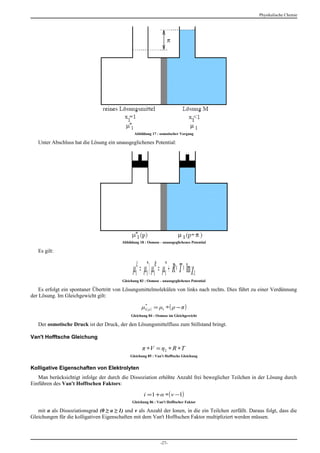


![Physikalische Chemie
2. Einfluss von Temperaturänderungen
0
δU k ΔH R
=
δT ρ R ∗T
2
k 2 ΔH R 1
0
1
ln = ∗ −
T T
k1 R 1 2
Gleichung 94 : Gleichgewicht: Einfluss von Temperaturänderungen
Bei Temperaturerhöhung wird also die endotherme Reaktion begünstigt, bei Temperaturerniedrigung die
exotherme Reaktion.
3. Einfluss von Komponentenänderungen
Der Zusatz einer Komponente begünstigt die Reaktion, die diesen Stoff verbraucht beziehungsweise begünstigt
der Entzug einer Komponente die Reaktion, die diesen Stoff bildet.
Löslichkeitsprodukt
Ein einem heterogenen Gleichgewicht
AgCl ( s ) ⇔ Ag + + Cl −
Formel 3 : Dissoziationsgleichgewicht von Silberchlorid
mit
K=
[ Ag ] ∗[Cl ]
+ −
[ AgCl ]
Gleichung 95 : Gleichgewichtskonstante von Silberchlorid
können wir [AgCl] als konstant ansehen. Die Lösung ist also vollständig gesättigt. Um wissen zu können, wie gut sich
ein Stoff löst, definieren wir das Löslichkeitsprodukt KL für Stoffe der allgemeinen Summenformel AXBY:
K L = K ∗ [ AX BY ] = [ A] ∗ [ B ]
X Y
Gleichung 96 : Löslichkeitsprodukt
Also für unser Beispiel mit Silberchlorid
[
K L = K ∗ [ AgCl ] = Ag + ∗ Cl − ] [ ]
Gleichung 97 : Löslichkeitsprodukt von AgCl
( X +Y )
mol
Das Löslichkeitsprodukt wird in der Einheit angegeben. KL-Werte sind immer temperaturabhängig. Sie
l
werden gewöhnlich als Tabellenwerte bei 298 K angegeben.
Ionenprodukt des Wassers
Wasser bildet mit Protonen und Hydroxidionen ein Gleichgewicht:
H 2 O ⇔ H + + OH −
Formel 4 : Dissoziationsgleichgewicht von Wasser
Die Gleichgewichtskonstante ist somit
K=
[ H ] ∗ [OH ]
+ −
[ H 2O ]
Gleichung 98 : Gleichgewichtskonstante von Wasser
Die Konzentration [H2O] ist in verdünnten wässrigen Lösungen sehr hoch (55,5 Mol*l-1) und bleibt nahezu konstant. Es
folgt das Ionenprodukt des Wassers:
[ ] [
K W = K ∗ [ H 2 O ] = H + ∗ OH − ]
Gleichung 99 : Ionenprodukt des Wassers
Das Ionenprodukt ist wie das Löslichkeitsprodukt temperaturabhängig:
T [K] 273 298 313 373
KW [mol2*l-2 0,12*10-14 1*10-14 2,9*10-14 5,4*10-13
-30-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-26-320.jpg)
![Physikalische Chemie
Tabelle 8 : Ionenprodukt des Wassers bei verschiedenen Temperaturen
Schreibt man das Ionenprodukt logarithmisch, erhält man
ρK H 2O = ρH + ρOH
Gleichung 100 : Ionenprodukt des Wassers, logarithmiert
Pufferlösungen
Pufferlösungen halten den pH-Wert bei begrenztem Zusatz von Säuren und Laugen konstant. Im menschlichen Blut
hält ein Bikarbonat-Puffer den pH ≈ 7,4.
Ein Essigsäure-Acetat-Puffer hält den pH ≈ 4,76. Bei Zugabe von Säure puffert die konjugierte Base
CH 3 COO − + H 3 O + ⇔ CH 3 COOH + H 2 O
Formel 5 : Essigsäure-Acetat-Puffer bei Zugabe von Säure
bei Zugabe von Lauge die Säure
CH 3 COOH + OH + ⇔ CH 3 COO − + H 2 O
Formel 6 : Essigsäure-Acetat-Puffer bei Zugabe von Lauge
Die Wirkungsweise lässt sich aus dem Massenwirkungsgesetz herleiten:
K S = K ∗ [ H 2O ] =
[ H O ] ∗ [CH COO ]
3
+
3
−
[ CH 3COOH ]
Gleichung 101 : Säurestärke von Essigsäure
KS bezeichnet die Säurestärke. Durch Umstellung und Logarithmierung erhält man die Henderson-Hasselbalch-
Gleichung:
pH = pK S + log
[CH COO ] 3
−
[ CH 3COOH ]
Gleichung 102 : pH-Wert (Henderson-Hasselbalch-Gleichung)
Beispiel: Eine Pufferlösung enthält 1 Mol*l-1 Essigsäure (pKS = 4,76) und 1 Mol*l-1 Natriumacetat. Welchen pH-Wert
hat
1. dieser Puffer?
2. die Lösung nach Zugabe von x = 0,1 Mol*l-1 HCl?
3. die Lösung nach Zugabe von y = 0,1 Mol*l-1 NaOH?
Wir stellen zunächst eine kleine Tabelle auf, die die Veränderungen erfasst:
Konzentration in mol*l-1 [CH3COOH] [CH3COO-]
1. Pufferlösung 1,0 1,0
2. Zugabe von HCl 1,0 + x 1,0 – x
3. Zugabe von NaOH 1,0 - y 1,0 + y
Tabelle 9 : Pufferveränderungen bei Zugabe von Säure oder Lauge
Damit ergeben sich laut Gl. 102:
1. pH = pKS = 4,76
2. pH = 4,76 + log 0,9/1,1 = 4,67
3. pH = 4,76 + log 1,1/0,9 = 4,85
Protolytische Gleichgewichte von Aminosäuren
Aminosäuren besitzen zwei Gruppen, die reagieren können: eine saure Carbonsäuregruppe und eine basische
Aminogruppe. Je nach pH der umgebenden Lösung kann die Aminosäure als reines Kation (Carbonsäuregruppe und
Aminogruppe protoniert), als Zwitterion (Carbonsäuregruppe deprotoniert, Aminogruppe protoniert) oder als Anion
(Carbonsäuregruppe und Aminogruppe deprotoniert) vorliegen. Für die Übergänge gibt es folglich zwei Säurestärken: Für
den Übergang vom Kation zum Zwitterion ist (für Glycin) pK1 = 2,35, für den Übergang vom Zwitterion zum Anion
pK2 = 9,6.
Der isoelektrische Punkt liegt dann vor, wenn genau so viele Kationen wie Anionen in der Lösung vorliegen:
-31-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-27-320.jpg)
![Physikalische Chemie
[ Kation ] = [ Anion ]
K1 ∗ K 2 = H + [ ] 2
log K1 + log K 2 = 2 ∗ log H + [ ]
Gleichung 103 : Isoelektrischer Punkt 1
Der isoelektrische Punkt liegt also bei
1
pH ( IP ) = ∗ ( pK1 + pK 2 )
2
Gleichung 104 : Isoelektrischer Punkt 2
Für Glycin ist dies ≈ 5,98.
Abbildung 20 : Isoelektrischer Punkt
-32-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-28-320.jpg)

![Physikalische Chemie
ΔE 0 = E 0 ( Kathode ) − E 0 ( Anode )
Gleichung 109 : Standard-EMK
E sind die Reaktanden in Standardzuständen bei T = 298 K. Die Werte für Standardpotentiale E0 ergeben sich aus
0
Tabellen (Spannungsreihe, Bezugselektrode ist die Standard-Wasserstoffelektrode). Die maximale Arbeit, die mit einer
Zelle geleistet werden kann, entspricht unter isotherm-isobaren Bedingungen der Abnahme der freien Enthalpie des
Systems:
ΔG0 = −n ∗ r ∗ ΔE
Gleichung 110 : Maximale Arbeit einer Zelle unter isotherm-isobaren Bedingungen
mit n der Anzahl der Elektronenmol. Das heißt, nur bei ΔE > 0 läuft die Reaktion freiwillig ab.
Beispiel:
E 0 ( Cu/Cu 2+ ) = 0,34[V ]
E 0 ( Zn/Zn 2+ ) = −0,76[V ]
ΔE 0 = 1,10[V ]
As ∗ V kJ
ΔG0 = −2 ∗ 96485 ∗1,1 = 212,3
mol mol
Gleichung 111 : Maximale Arbeit des Daniell-Element
Die Nernstsche Gleichung
Berechnung der EMK ΔE, wenn beteiligte Stoffe nicht in Standardzuständen vorliegen:
rA ∗ A + rB ∗ B ⇒ rP ∗ P + rQ ∗ Q
r r
c PP ∗ cQQ
r
c PP ∗ cQQ
r
ΔGR = ΔG + R ∗ T ∗ ln
0
R = − n ∗ F ∗ ΔE = − n ∗ F ∗ ΔE + R ∗ T ∗ ln
0
c A ∗ c AA
rA r
c A ∗ c AA
rA r
r
R∗T cPP ∗ cQQ
r
ΔE = ΔE − 0
∗ ln rA rA
n∗ F cA ∗ cA
Gleichung 112 : EMK, wenn Stoffe nicht in Standardzuständen vorliegen
Durch Einsetzen der Konstanten und der Temperatur T = 298 K sowie Umformung des natürlichen in den dekadischen
Logarithmus erhält man die Nernstsche Gleichung:
0,059[V ]
r
c PP ∗ cQQ
r
ΔE = ΔE + 0
∗ log rA rA
n cA ∗ cA
Gleichung 113 : Nernstsche Gleichung
Beispiel: Welche EMK hat die Zelle
mol 2+ mol
Sn/Sn 2+ 1 //Pb 0,001 /Pb
l l
bei T = 298 K?
Sn ⇒Sn 2+ + 2e − E 0 (Sn/Sn 2+ ) = −0,136V( Anode)
Pb 2+ + 2e − ⇒ Pb E 0 ( Pb/Pb 2+ ) = −0,126V( Kathode )
Sn + Pb 2+ ⇒Sn 2+ + Pb ΔE 0 = 0,01V
ΔE = ΔE 0 −
0 ,059 2+
[ ]
[V ] ∗log Sn 2+ = 0,01[V ] − 0,059 [V ] ∗log 1,0 = 0,079[V ]
2 Pb [ ] 2 0 ,001
Gleichung 114 : Umkehrung der Polung durch Konzentrationseffekte
Die Reaktion läuft nicht freiwillig ab. Das heißt, die Gegenreaktion tritt ein. Die Polung der Zelle wird gegenüber der
Zelle unter Standardbedingungen durch die Konzentrationseffekte umgekehrt.
-34-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-30-320.jpg)


![Physikalische Chemie
Transporterscheinungen
Viskosität
In Gasen und Flüssigkeiten wird die Strömung durch Adhäsions- und Kohäsionskräfte behindert. Wir unterscheiden
zwischen
● laminarer Strömung (parabolische Geschwindigkeitsverteilung)
Abbildung 28 : Laminare Strömung
und
● turbulenter Strömung (unregelmäßige Geschwindigkeitsverteilung, Wirbel)
Abbildung 29 : Turbulente Strömung
Die folgenden Ausführungen setzen laminare Strömungen voraus. Diese wird am besten durch kleine Rohrdurchmesser
und eine kleine Durchflussgeschwindigkeit erreicht.
Die dynamische Viskosität η ist die Kraft, die benötigt wird um in einem Gas bzw. in einer Flüssigkeit eine ebene
Platte der Fläche A parallel zu einer ebenen Wand im Abstand l mit konstanter Geschwindigkeit ν entlangzuziehen.
ν
F = η∗ A∗
l
Gleichung 119 : Dynamische Viskosität
-1 2 -1
mit [η] = 1P [Poise] = 10 [N*s/m ] = 10 [Pa*s].
Die kinematische Viskosität berechnet sich nun folgendermaßen:
η
ν=
ρ
Gleichung 120 : Kinematische Viskosität
Beim Fließen durch eine Röhre der Länge l und dem Radius r, an deren Enden die Drücke p1 bzw. p2 herrschen, gilt für
das pro Zeitinterwall Δt durchfließende Volumen ΔV:
π ∗ ( p1 − p 2 ) ∗ r 4
ΔV =
8∗η∗ ρ
Gleichung 121 : Hagen-Poiseuillsche-Gesetz
Die Gl. 121 wird als das Hagen-Poiseuillsche-Gesetz bezeichnet. Als erste Näherung gilt ΔV ≈ r4:
Die Viskosität ist eine stoff- und temperaturabhängige Größe. Bei Flüssigkeiten sinkt die Viskosität mit steigender
Temperatur infolge der abnehmenden Reibung, es erhöht sich dann die Flüchtigkeit. Bei Gasen verhält es sich umgekehrt.
-37-](https://image.slidesharecdn.com/physikalischechemie-130203105522-phpapp02/85/Physikalische-Chemie-33-320.jpg)









