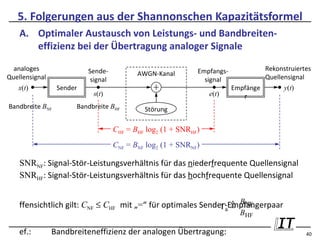
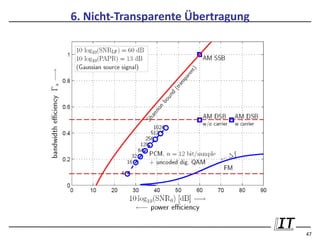
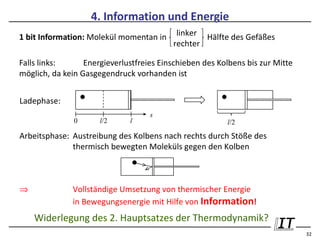
Das Dokument thematisiert die revolutionären Auswirkungen der Kapazitätsformel von Claude Shannon auf die Informationsübertragung. Es behandelt die Grundlagen der Informationstheorie, die Rolle von Energie in der Informationsübertragung sowie die wesentlichen Entwicklungen im Informationszeitalter. Insbesondere wird die Umstellung von analoger auf digitale Informationstechnik und deren Effizienz hervorgehoben.

1. Eine Formel verändert die Welt
5 Jahre
Institut für Vernetzte und Eingebettete
Systeme
an der Alpen-Adria-Universität
Klagenfurt
Johannes Huber
Lehrstuhl für Informationsübertragung
Friedrich-Alexander-Universität Erlangen-Nürnberg
21. Juni 2012

2. Eine Formel verändert die Welt
Inhaltsübersicht
2. Die Säulen des Informationszeitalters
4. Die Kapazitätsformel
5. Grundlagen der Informationstheorie
A. Gesetz der großen Zahlen
B. Kugeln im vieldimensionalen Raum
6. Information und Energie
A. Minimale Energie pro bit Information bei thermischem Rauschen
B. Information und der 2. Hauptsatz der Thermodynamik (Maxwellscher Dämon)
2

3. Eine Formel verändert die Welt
1. Folgerungen aus der Shannonschen Kapazitätsformel
A. Leistungs- und Bandbreiteneffizienz bei der digitalen Übertragung
B. Digitalisierung analoger Werte
C. Austausch von Leistungs- und Bandbreiteneffizienz bei der Übertragung
analoger Signale
2. Nicht-transparente Informationsübertragung: Quellencodierung
A. Redundanzreduktion
B. Irrelevanzreduktion
3. Formeln verändern die Welt
3

4. Eine Formel verändert die Welt
Äquivalenz von Masse und Energie: E = m · c2
4

5. 1. Die Säulen des Informationszeitalters
Radio des Jahres 1960
5

6. 1. Die Säulen des Informationszeitalters
Inneres des I-Phones 2010
Wodurch wurde diese Entwicklung innerhalb von 50 Jahren ermöglicht?
6

7. 1. Die Säulen des Informationszeitalters
• Erfindung des Transistors
Bardeen, Brattain, Shockley, AT & T Bell Labs, Murray Hill, New Jersey,
1947/48
⇒ Entwicklung der Mikroelektronik
Lösung des Problems: Wie können informationstechnische Systeme
effizient implementiert werden?
• Entwicklung der Informationstheorie durch
Claude E. Shannon (1916 – 2001)
AT & T Bell Labs, Murray Hill, New Jersey, 1948 (publiziert)
Antwort auf die Frage: Was ist ein effizientes informationstechnisches
System, aus welchen Komponenten soll es bestehen, welche Methoden
sind anzuwenden?
⇒ Einleitung des Wandels von der analogen zur digitalen
Informationstechnik durch eine
Mathematische Theorie 7

8. 1. Die Säulen des Informationszeitalters
Claude Elwood Shannon
1916 - 2001
8

9. 1. Die Säulen des Informationszeitalters
The Father of
Information Age
9

10. 1. Die Säulen des Informationszeitalters
10

11. 1. Die Säulen des Informationszeitalters
11

12. Eine Formel verändert die Welt
Inhaltsübersicht
• Die Säulen des Informationszeitalters
• Die Kapazitätsformel
• Grundlagen der Informationstheorie
A. Gesetz der großen Zahlen
B. Kugeln im vieldimensionalen Raum
6. Information und Energie
A. Minimale Energie pro bit Information bei thermischem Rauschen
B. Information und der 2. Hauptsatz der Thermodynamik (Maxwellscher Dämon)
12

13. 2. Die Kapazitätsformel
Eine Formel hat die Welt grundlegend verändert:
unabhängige Gauß´sche
Störvariable
gestörte
2
Nachrichtenübertragung W σW = N
X Y
2 2
σX = S σY = S + N
1 S bit
C = log 2 1 + 
 
2  N  Wert
C: Informationsübertragungskapazität des zeitdiskreten Kanals
bei additiver Gauß´scher Störung
S: Varianz des Nutzsignals (Nutzsignalleistung: Signal Power)
N: Varianz der Störung (Störsignalleistung: Noise Power)
13

14. 2. Die Kapazitätsformel
Durch Anwendung des Abtasttheorems:
Bei einem auf die Spektralbandbreite B bandbegrenztem Signal sind
maximal 2 · B Werte je Sekunde frei wählbar.
folgt
S  S  bit
CT = B log 2 1 +  = B log 2 1 +
  
 BN  Sekunde
 N  0
CT: Informationsübertragungskapazität des zeitkontinuierlichen,
bandbegrenzten Übertragungskanals mit Störung durch weißes,
Gauß´sches Rauschen
B: (einseitige) spektrale Signalbandbreite
N0: (einseitige) spektrale Rauschleistungsdichte
14

15. 2. Die Kapazitätsformel
Fundamentale Einsichten:
Beim Vorhandensein von Störungen kann auch durch analoge, d.h.
wertkontinuierliche Signalwerte nur eine begrenzte Anzahl unterschiedlicher
Informationen repräsentiert und übertragen werden:
⇒ Information ist in digitaler Form zu repräsentieren
und zu übertragen
Trotz Störungen kann aber Information zuverlässig, absolut fehlerfrei
übertragen werden:
⇒ eine effiziente Informationstechnik ist eine digitale
Informationstechnik
15

16. 2. Die Kapazitätsformel
Fundamentaler Unterschied zwischen analoger und digitaler
Informationstechnik:
analog: Nutzsignal und Störung sind empfangsseitig
nicht mehr trennbar
digital: Nutzsignal und Störung sind prinzipiell
wieder trennbar.
Digitale Informationstechnik erlaubt Signalregeneration: Fehlerfreie Detektion
der digitalen Symbolsequenzen und erneutes Senden des störungsfreien
Sendesignals.
Beispiele: Kopieren von CDs (im Vergleich zu analogen Audiokassetten)
Telefonieren nach Australien
16

17. Eine Formel verändert die Welt
Inhaltsübersicht
• Die Säulen des Informationszeitalters
• Die Kapazitätsformel
• Grundlagen der Informationstheorie
– Gesetz der großen Zahlen
– Kugeln im vieldimensionalen Raum
6. Information und Energie
A. Minimale Energie pro bit Information bei thermischem Rauschen
B. Information und der 2. Hauptsatz der Thermodynamik (Maxwellscher Dämon)
17

18. 3. Grundlagen der Informationstheorie
A. Gesetz der großen Zahlen
Wird ein Zufallsexperiment (statistisch unabhängig) sehr oft wiederholt,
dann nähern sich relative Häufigkeiten Wahrscheinlichkeiten an,
Mittelwerte streben gegen Erwartungswerte usw.
Wiederholung reduziert die Zufälligkeit
(vgl. Versicherungen)
18

19. 3. Grundlagen der Informationstheorie
Beispiel: Fairer Münzwurf, Zufallsereignis: Wappen (Kopf) oder Zahl
Wahrscheinlichkeit für W Wappen bei n Würfen Pr (W) = ( W) 2
n -n
n = 100000
10
100
10000
1000 nn =100
= 10
0 0 10 1 20 2 30 3 404 50
5 6
60 7 70 8 80 9 90 10 100
·105
19

20. 3. Grundlagen der Informationstheorie
B. Kugeln in vieldimensionalen Euklidischen Räumen ℝn

Ein Punkt x = ( x1 , x2 , x3 ,, xn ) im ℝn wird durch n Koordinaten spezifiziert.
n
 2 2
Def.: Kugel mit Radius R: Menge aller Punkte x mit ∑ xi = R
i =1
x2 R
. Satz von
Beispiel n = 2 x1 + x2 = R 2
2 2
x1 Pythagoras!
Volumen V einer Kugel mit Radius R im ℝn
n=2 V = π R2
π n/2
V= ⋅ Rn π 3/ 2 4
( n / 2) ! n=3 V= R3 = π R3
(3 / 2)! 3
Für eine sehr große Zahl n von Dimension (n >> 1) gilt:
Das Kugelvolumen wird im Wesentlichen durch oberflächennahe Punkte
dominiert.
20

21. 3. Grundlagen der Informationstheorie
(Mittelwertfreie) informationstragende Signalwerte xi: Zufallswerte mit
2 2
Varianz σ x = E{x } = S (mittlere Signalleistung)
xi
2
i
1 3 4 5
1 n 2 1 2 2
Gesetz der großen Zahlen: ∑ xi strebt für n → ∞ nach ⋅ nσ x = σ x = S
n i =1 n

Für jede lange Folge von Signalwerten xi besitzt der zugehörige Vektor x
den Betrag  2
x ≅ n ⋅σ x
⇒ Alle informationstragenden langen Folgen liegen im ℝn auf der
Oberfläche bzw. in einer Kugel mit dem Radius
R= n⋅S
21

22. 3. Grundlagen der Informationstheorie
x2
x1
x3
22

23. 3. Grundlagen der Informationstheorie
Einfaches Übertragungsmodell
Addition statistisch unabhängiger Störwerte
X Y
gesendeter Wert empfangener Wert
2 2
mit Varianz σ x = S Wi mit Varianz σ y = S + N
Störung mit
2
Varianz σ w = N
Übertragung langer Folgen von Werten (n >> 1) :

Alle empfangenen Folgen y = ( y1 , y 2 , y3 , , y n ) bilden im ℝn Punkte auf, bzw.
in einer Kugel mit dem Radius n ⋅ ( S + N ) und dem Volumen Vy .

Alle Störungen w = ( w1 , w2 , , wn ) bilden im ℝn Punkte auf bzw. in einer Kugel
mit dem Radius nN und dem Volumen V . w

Um jeden gesendeten Punkt x bildet die Störung eine Rauschkugel,

innerhalb derer der empfangene Punkt y für n → ∞ zu finden ist.
23

24. 3. Grundlagen der Informationstheorie
Illustration n = 2 x2 
w

x2 
w

x1
In einer großen Kugel mit dem Volumen Vy
x1
haben maximal L = Vy /Vw kleine Kugeln
mit dem Volumen Vw Platz
Damit können höchstens
π n/2
Vy (n / 2)!
( n ⋅ (S + N )) n / 2 n/2
 S
L= = = 1 + 
Vw π n/2  N
( n ⋅ N )n/2
(n / 2)!
unterschiedliche Nachrichten trotz des Vorhandenseins von Störungen
fehlerfrei unterscheidbar übertragen werden, wenn sich die zugehörigen
Rauschkugeln für n → ∞ nicht wechselseitig durchdringen.
(„Sphere Hardening“) .
24

25. 3. Grundlagen der Informationstheorie
NB: Für die Bezeichnung (Adressierung) von L Elementen einer Menge benötigt
man log2 (L) Binärsymbole (Bits: High/Low oder 0/1 oder schwarz/weiß)
Zahl der durch ein Wort der Länge n übertragbaren Bits
Z ≤ log 2 ( L )
Zahl der je einzelnem Wert übertragbaren Bits
1
( )
Z n ≤ log 2 ( L ) = log 2 L1/ n
n
1/ n
 S  
n
 S 
Z ≤ log 2   1 +    1+ 
= log 2 
 N  N
     
1  S bit
Z ≤ log 2 1 + 
2  N Kanalbenutzung
(Umkehrung des Kanalcodierungstheorems)
25

26. 3. Grundlagen der Informationstheorie
Methode zum Beweis des Kanalcodierungstheorems:
Für Gauß-verteilte Zufallsvariablen xi erhält man im ℝn, n → ∞, auf der
2
Oberfläche einer Kugel mit dem Radius n ⋅σ x
gleichmäßig verteilte Signalpunkte

Eine Auswahl von L = (1 + S/N)n/2 Punkten x ist damit so möglich, dass sich
die zugehörigen „Rauschkugeln“ nicht durchdringen und eine fehlerfreie
Unterscheidung der L Nachrichten möglich wird.
C = log 2 1 + 
1 S bit
 
2  N Kanalbenutzung
26

27. Eine Formel verändert die Welt
Inhaltsübersicht
2. Die Säulen des Informationszeitalters
4. Die Kapazitätsformel
5. Grundlagen der Informationstheorie
A. Gesetz der großen Zahlen
B. Kugeln im vieldimensionalen Raum
6. Information und Energie
A. Minimale Energie pro bit Information bei thermischem Rauschen
B. Information und der 2. Hauptsatz der Thermodynamik (Maxwellscher Dämon)
27

28. 4. Information und Energie
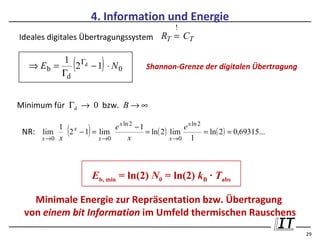
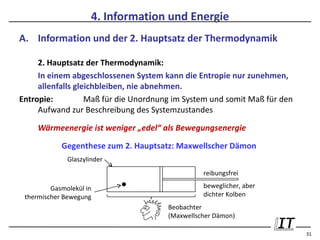
A. Minimale Energie pro bit bei thermischem Rauschen
Störung:
Störleistung N = N0 · B mit N0: (einseitige) Rauschleistungsdichte von
thermischen Rauschen, B: Signalbandbreite W
−23
klassische Physik: N0 = kB Tabs mit kB = 1,38 10 Hz K Boltzmann-Konstante
Tabs = 292 K : N0 = 4 · 10−21 W
Hz
Nutzsignal: Eb: Energie pro bit Information; Tb: Zeit pro bit:
Eb = S · Tb
 bit 
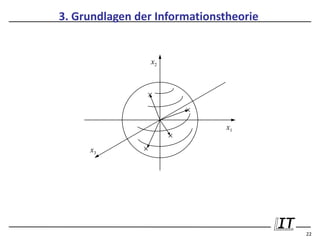
Datengeschwindigkeit (Datenrate) RT = 1 / Tb  s 
 
Spektrale Effizienz Γd =
ˆ
RT
B
[ bit/s ]
Hz
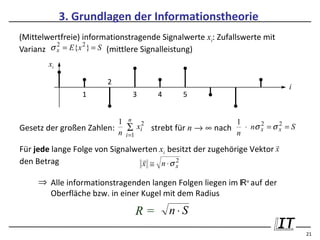
 E 
⇒ CT = B log 2 1 + Γd b 

 N0 
28

29. 4. Information und Energie
!
Ideales digitales Übertragungssystem RT = CT
⇒ Eb =
1 Γd
Γd
(
2 − 1 ⋅ N0 ) Shannon-Grenze der digitalen Übertragung
Minimum für Γd → 0 bzw. B → ∞
NR: lim
x →0
1 x
x
(
2 − 1 = lim
x →0
)e x ln 2 − 1
x
= ln ( 2 ) lim
x →0
e x ln 2
1
= ln ( 2 ) = 0,69315...
Eb, min = ln(2) N0 = ln(2) kB · Tabs
Minimale Energie zur Repräsentation bzw. Übertragung
von einem bit Information im Umfeld thermischen Rauschens
29

30. 4. Information und Energie
Materie Energie
Masse m E = mc2 Energie E
m T ab s
b,m kB
in = c -2
n (2 )
·E
b,m n
=l
i
in
E b,m
Information
Tabs = 293 K: Eb,min = 2,793 · 10−21 J
mb,min = 3,10 · 10−38 kg
aber:
Quantenphysikalische Effekte berücksichtigen!
30

31. 4. Information und Energie
A. Information und der 2. Hauptsatz der Thermodynamik
2. Hauptsatz der Thermodynamik:
In einem abgeschlossenen System kann die Entropie nur zunehmen,
allenfalls gleichbleiben, nie abnehmen.
Entropie: Maß für die Unordnung im System und somit Maß für den
Aufwand zur Beschreibung des Systemzustandes
Wärmeenergie ist weniger „edel“ als Bewegungsenergie
Gegenthese zum 2. Hauptsatz: Maxwellscher Dämon
Glaszylinder
reibungsfrei
Gasmolekül in beweglicher, aber
thermischer Bewegung dichter Kolben
Beobachter
(Maxwellscher Dämon)
31

32. 4. Information und Energie
1 bit Information: Molekül momentan in linker Hälfte des Gefäßes
rechter
Falls links: Energieverlustfreies Einschieben des Kolbens bis zur Mitte
möglich, da kein Gasgegendruck vorhanden ist
Ladephase:
s
0 l/2 l l/2
Arbeitsphase: Austreibung des Kolbens nach rechts durch Stöße des
thermisch bewegten Moleküls gegen den Kolben
⇒ Vollständige Umsetzung von thermischer Energie
in Bewegungsenergie mit Hilfe von Information!
Widerlegung des 2. Hauptsatzes der Thermodynamik?
32

33. 4. Information und Energie
Gegen den 2. Hauptsatz gewonnene Bewegungsenergie EMD
l
E MD = ∫ F ( s ) ⋅ ds
l /2
Kraft mal Weg
33

34. 4. Information und Energie
Isotherme Expansion: Boyle-Mariottsches Gesetz (1662, 1676) für das ideale
Gas und Maxwell-Boltzmann-Verteilung (1860)
p · V = z · kB Tabs hier z = 1 (Energie je Molekül)
Druck p = F(s)/A mit A: Querschnittsfläche des Zylinders
k B ⋅ Tabs
Volumen V(s) = A · s ⇒ F(s) · s = kB · Tabs ⇒ F ( s) =
s
l k B Tabs l 
= k B Tabs ln  = k B Tabs ln ( 2 )
l
E MD = ∫ ds = k B Tabs ln( s ) l /2 
l /2 s l /2
EMD = ln(2) kB · Tabs = ln(2) N0 = Eb,min
34

35. 4. Information und Energie
Es wird durch 1 bit Information genau die Energie im Widerspruch zum
2. Hauptsatz der Thermodynamik gewonnen, die zur Repräsentation bzw.
Übertragung von 1 bit Information minimal notwendig ist.
⇒ Maxwellscher Dämon ist widerlegt.
Fundamentaler Zusammenhang zwischen Energie und Information bestätigt!
Beispiel zur Ästhetik der Wissenschaften
35

36. Eine Formel verändert die Welt
1. Folgerungen aus der Shannonschen Kapazitätsformel
– Leistungs- und Bandbreiteneffizienz bei der digitalen Übertragung
– Digitalisierung analoger Werte
– Austausch von Leistungs- und Bandbreiteneffizienz bei der Übertragung
analoger Signale
2. Nicht-transparente Informationsübertragung: Quellencodierung
A. Redundanzreduktion
B. Irrelevanzreduktion
4. Formeln verändern die Welt
36

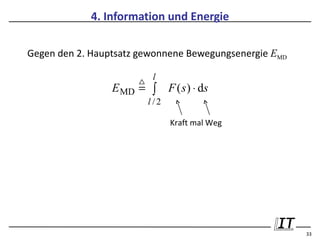
37. 5. Folgerungen aus der Shannonschen Kapazitätsformel
A. Zusammenhang zwischen Leistungs- und
Bandbreiteneffizienz bei der digitalen Übertragung
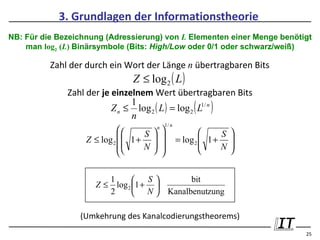
Shannon-Grenze:
Eb
N0
≥
1
Γd
( )
2 Γd − 1
10log10(Eb/N0) [dB] →
← power efficiency
37

38. 5. Folgerungen aus der Shannonschen Kapazitätsformel
A. Optimale Digitalisierung
Analogwerte Daten Diskrete Werte
X Digitalisierung Rekonstruktion Y
X∈ ℝ R bit/Wert Y∈{y1, y2, ..., yM}
Kapazität für eine digitale Übertragung
C = 1/2 log2 (1 + S/N)
{ 2}
Signalleistung S = E X = σ x
2
Störung W =Y − X Störleistung N = E{(Y – X)2}
S
Signal-Stör-Leistungsverhältnis (Signal to Noise Ratio): SNR =
N
• Offensichtlich gilt: Je Wert X kann (im Mittel) nicht mehr
Information von Ende zu Ende (X → Y) übertragen werden, als
Information in Form von Daten transportiert wird (Data Processing
Theorem).
R ≥ C = R ≥ 1/2 log2 (1 + SNR)
38

39. 5. Folgerungen aus der Shannonschen Kapazitätsformel
A. Optimale Digitalisierung
Rate-Distortion Grenze für die
SNR ≤ 22R − 1
Digitalisierung unabhängiger Zufallswerte!
Weg zur optimalen Digitalisierung: Vektorquantisierung im ℝn mit n → ∞
39

40. 5. Folgerungen aus der Shannonschen Kapazitätsformel
A. Optimaler Austausch von Leistungs- und Bandbreiten-
effizienz bei der Übertragung analoger Signale
analoges Sende- Empfangs- Rekonstruiertes
Quellensignal AWGN-Kanal Quellensignal
signal signal
x(t) Sender Empfänge y(t)
s(t) e(t) r
Bandbreite BNF Bandbreite BHF Störung
CHF = BHF log2 (1 + SNRHF)
CNF = BNF log2 (1 + SNRNF)
SNRNF: Signal-Stör-Leistungsverhältnis für das niederfrequente Quellensignal
SNRHF: Signal-Stör-Leistungsverhältnis für das hochfrequente Quellensignal
B
ffensichtlich gilt: CNF ≤ CHF mit „=“ für optimales Sender-Empfängerpaar
Γa = NF
BHF
ef.: Bandbreiteneffizienz der analogen Übertragung: 40

41. 5. Folgerungen aus der Shannonschen Kapazitätsformel
A. Optimaler Austausch von Leistungs- und Bandbreiteneffizienz bei
der Übertragung analoger Signale
Shannon-Grenze der analogen Übertragung CNF = CHF
SNRNF = (1 + SNRHF)1/Γ a − 1
Das gleiche Resultat gilt für die Kombination „Optimale Digitalisierung“ mit
„optimaler digitaler Übertragung“:
⇒ Theorem der Trennbarkeit von Quellencodierung
und digitaler Übertragung
41

42. 5. Folgerungen aus der Shannonschen Kapazitätsformel
Leistungs-Bandbreiten-Diagramm für die Übertragung analoger Signale
42

43. Eine Formel verändert die Welt
1. Folgerungen aus der Shannonschen Kapazitätsformel
A. Leistungs- und Bandbreiteneffizienz bei der digitalen Übertragung
B. Digitalisierung analoger Werte
C. Austausch von Leistungs- und Bandbreiteneffizienz bei der Übertragung
analoger Signale
2. Nicht-transparente Informationsübertragung: Quellencodierung
A. Redundanzreduktion
B. Irrelevanzreduktion
4. Formeln verändern die Welt
6. Persönliche Anmerkungen
43

44. 6. Nicht-Transparente Übertragung
Die Shannon-Grenze gilt für die transparente Übertragung analoger Signale,
also für jedes Quellensignal mit einer Bandbreite ≤ BNF
⇒Einschränkung auf typische Signale, z.B. Audiosignale
⇒ Nicht-transparente Verfahren
44

45. 6. Nicht-Transparente Übertragung
– Quellencodierung zur Redundanz-Reduktion:
Übertragung von typischen Symbolfolgen oder Signalen
Repräsentation langer Folgen durch nH anstelle n log2(M) Binärsymbole
Menge aller Mn Folgen
Teilmenge der von
der Quelle typischen
2nH Folgen
45

46. 6. Nicht-Transparente Übertragung
r Quellencodierung zur Irrelevanz-Reduktion:
Der Empfänger ist nicht in der Lage, alle möglichen Mn unterschiedlicher
Folgen zu unterscheiden, sondern nur 2 nH irr
Menge aller Mn Folgen
Teilmenge der vom
Empfänger
unterscheidbaren 2nH
irr
Folgen
Teilmenge für die
typischen vom
Empfänger
unterscheidbaren
Folgen
Redundanz + Irrelevanz-Reduktion: Es reichen im Mittel H – (log2(M) – Hirr)
Binärsymbole je Quellensymbol
46

47. 6. Nicht-Transparente Übertragung
47

48. Eine Formel verändert die Welt
1. Folgerungen aus der Shannonschen Kapazitätsformel
A. Leistungs- und Bandbreiteneffizienz bei der digitalen Übertragung
B. Digitalisierung analoger Werte
C. Austausch von Leistungs- und Bandbreiteneffizienz bei der Übertragung
analoger Signale
2. Nicht-transparente Informationsübertragung: Quellencodierung
A. Redundanzreduktion
B. Irrelevanzreduktion
• Formeln verändern die Welt
48

49. 7. Formeln verändern die Welt
Technische Revolutionen wurden und werden immer durch
fundamentale theoretische Leistung
erreicht, nicht durch Tüftler und Bastler etc.
Thermodynamik (Carnotscher Kreisprozess): effiziente
Wärmekraftmaschinen
Elektrodynamik (Maxwellsche Gleichungen): Elektrotechnik
Quantenmechanik (Festkörperphysik): Mikro-/Nano-Elektronik
Informationstheorie: Digitale Informationstechnik
„Eine gute Theorie ist das praktischste, was es gibt“
(G. R. Kirchhoff, 1824 – 1887)
Shannon: „I never in my life tried to do anything useful.“ ...
49

50. 7. Formeln verändern die Welt
Nicht „Produkte“ der Finanzwelt,
nicht Ideologien,
nicht Fußballstars und auch nicht andere Stars,……
verändern die Welt so sehr wie
Formeln und die hieraus folgende Technik
aber:
Technik ist grundsätzlich ambivalent
Naturwissenschaftler und Techniker haben keine Macht darüber, wozu
Formeln und die hieraus entstehende Technik benutzt werden.
⇒ Komplexere Technik erfordert zugleich eine
höhere kulturelle Entwicklung der Gesellschaft.
Die zentralen Aufgaben der Geisteswissenschaften:
Wertedefinition, Wertevermittlung!
Herzlichen Dank! 50