Datamics, profile picture
Hochgeladen vonDatamics
1,046 aufrufe

Principal Component Analysis mit Python

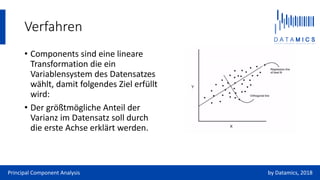
Die Hauptkomponentenanalyse (PCA) ist ein Verfahren der multivariaten Statistik, das zum Ziel hat, die Beziehung zwischen Variablen eines Datensatzes zu untersuchen, indem es umfangreiche Daten strukturiert und vereinfacht. Durch die Bestimmung orthogonaler Achsen wird eine maximale Varianz erklärt, was die Analyse und Interpretation von Daten erleichtert. Anwendungsbeispiele zeigen, wie PCA bei der Analyse von Schiffsdaten und Konsumverhalten eingesetzt werden kann, während die Interpretation der gewonnenen Komponenten eine Herausforderung darstellt.

Präsentation einbetten

Principal Component Analysis Eine Einführung
Mathematischer Hintergrund • Kapitel 10.2 im ISLR-Buch gibt einen tieferen Einblick in die Thematik Principal Component Analysis by Datamics, 2018
Übersicht • Lasst uns die grundsätzliche Idee hinter der PCA (deutsch Hauptkomponentenanalyse) besprechen. • Das mathematische Verfahren ist auch bekannt als Hauptachsentransformation oder Singulärwertzerlegung • Es ist eine „unsupervised“ multivarianten Statistik, um die Beziehung zwischen Variablen eines Datensatzes zu untersuchen. • Sie dient dazu, umfangreiche Datensätze zu strukturieren, zu vereinfachen und zu veranschaulichen • Sie ist auch manchmal als allgemeine Faktor Analyse bekannt. Principal Component Analysis by Datamics, 2018
Anwendungsbeispiel 1 Bei der Betrachtung von Schiffen wurden die Merkmale Länge, Breite, Wasserverdrängung, Tiefgang, Leistung der Maschinen, Geschwindigkeit (längerfristig mögliche Höchstgeschwindigkeit), erfasst. • Die Merkmale Länge, Breite, Wasserverdrängung und Tiefgang können so aufgefasst werden, dass sie alle einen ähnlichen Sachverhalt messen, den man als den Faktor „Größe“ beschreiben könnte. • Die Leistung der Maschinen und die Höchstgeschwindigkeit könnte zu einem Faktor „Geschwindigkeit“ zusammengefasst werden. Principal Component Analysis by Datamics, 2018
Anwendungsbeispiel 2 • Bei dem Kaufverhalten von Konsumenten, gibt es möglicherweise latente Faktoren wie sozialer Status, Alter oder Familienstand, die bestimmte Käufe motivieren. • Hier könnte man durch gezielte Werbung die “Kauflust” entsprechend kanalisieren. Principal Component Analysis by Datamics, 2018
Verfahren • Die bereits behandelte Regression bestimmt eine Linie, die den gesamten Datensatz bestmöglich repräsentiert. • Die PCA bestimmt mehrere orthogonale Linien, die das selbe tun sollen. • Orthogonal bedeutet „im rechten Winkel“. • Genau genommen sind die Linien senkrecht zueinander im n-dimensionalen Raum. • n-dimensionaler Raum ist der Raum der verschiedenen Variablen • Es gibt so viele Dimensionen wie es Variablen gibt. D.h. in einem Datensatz mit 4 Variablen gibt es auch 4 Dimensionen im Raum. Principal Component Analysis by Datamics, 2018
Verfahren • Hier sehen wir einige Daten entlang der beiden Features (bzw. Achsen) x und y dargestellt. Principal Component Analysis by Datamics, 2018
Verfahren • Wir können jetzt eine orthogonale Linie hinzufügen. • Jetzt können wir damit beginnen die “Components“ zu verstehen! Principal Component Analysis by Datamics, 2018
Verfahren • Components sind eine lineare Transformation die ein Variablensystem des Datensatzes wählt, damit folgendes Ziel erfüllt wird: • Der größtmögliche Anteil der Varianz im Datensatz soll durch die erste Achse erklärt werden. Principal Component Analysis by Datamics, 2018
Verfahren • Der zweitgrößte Anteil der Varianz im Datensatz soll durch die zweite Achse erklärt werden. • Und so weiter... • Dieser Prozess erlaub es uns die Anzahl an Variablen für spätere Analyse zu reduzieren. Principal Component Analysis by Datamics, 2018
Verfahren • Der zweitgrößte Anteil der Varianz im Datensatz soll durch die zweite Achse erklärt werden. • Und so weiter... • Dieser Prozess erlaub es uns die Anzahl an Variablen für spätere Analyse zu reduzieren. Principal Component Analysis by Datamics, 2018
Verfahren • Die Components sind dabei nicht korreliert, da sie im Raum der Samples gegeneinander orthogonal sind. Principal Component Analysis by Datamics, 2018
Verfahren • Und wir können diesen Prozess auch in höhere Dimensionen fortsetzen. Principal Component Analysis by Datamics, 2018
Verfahren • Wenn wir diese Technik jetzt auf einen Datensatz mit eine Vielzahl an Variablen anwenden, dann können wir die erklärte Varianz in einige wenige Components übertragen. • Die größte Herausforderung dabei ist es, die Components richtig zu interpretieren! Principal Component Analysis by Datamics, 2018
PCA mit Python • Für unsere Anwendung mit Python werden wir uns ein Beispiel einer PCA mit SciKit Learn anschauen. • Wir wollen dafür unsere Daten standardisieren, bevor wir sie in einer PCA verwenden, deshalb behandeln wir diesen Schritt ebenfalls. • Da dieser Algorithmus üblicherweise für Analyse von Daten und nicht für ein voll einsetzbares Modell wird es zu diesem Kapitel kein Portfolio Projekt geben. Principal Component Analysis by Datamics, 2018

Weitere ähnliche Inhalte

PPTX
Slideshare Recurrent Neural Networks (RNN)
vonDatamics
 
PPTX
Slideshare TensorFlow Grundlagen
vonDatamics
 
PPTX
Slideshare AutoEncoder
vonDatamics
 
PPTX
Die Data Science Softskills
vonDatamics
 
PDF
R für Data Science und Machine Learning
vonDatamics
 
PPTX
Slideshare reinforcement learning
vonDatamics
 
PPTX
Slideshare GAN
vonDatamics
 
PPTX
Die Data Science Toolbox
vonDatamics
 
Slideshare Recurrent Neural Networks (RNN)
vonDatamics
 
Slideshare TensorFlow Grundlagen
vonDatamics
 
Slideshare AutoEncoder
vonDatamics
 
Die Data Science Softskills
vonDatamics
 
R für Data Science und Machine Learning
vonDatamics
 
Slideshare reinforcement learning
vonDatamics
 
Slideshare GAN
vonDatamics
 
Die Data Science Toolbox
vonDatamics
 

Mehr von Datamics

PPTX
Python Bootcamp - Grundlagen
vonDatamics
 
PDF
Decision Trees und Random Forest mit Python
vonDatamics
 
PDF
Logistische Regression mit Python
vonDatamics
 
PDF
K Means mit Python
vonDatamics
 
PDF
Verzerrung Varianz Dilemma
vonDatamics
 
PDF
Support Vector Machines mit Python
vonDatamics
 
PDF
Machine Learning mit Python
vonDatamics
 
PDF
Python Installationen für Data Science
vonDatamics
 
PDF
K Nearest Neighbors mit Python
vonDatamics
 
PDF
Lineare Regression mit Python
vonDatamics
 
Python Bootcamp - Grundlagen
vonDatamics
 
Decision Trees und Random Forest mit Python
vonDatamics
 
Logistische Regression mit Python
vonDatamics
 
K Means mit Python
vonDatamics
 
Verzerrung Varianz Dilemma
vonDatamics
 
Support Vector Machines mit Python
vonDatamics
 
Machine Learning mit Python
vonDatamics
 
Python Installationen für Data Science
vonDatamics
 
K Nearest Neighbors mit Python
vonDatamics
 
Lineare Regression mit Python
vonDatamics
 

Principal Component Analysis mit Python

  • 1.
  • 2.
    Mathematischer Hintergrund • Kapitel10.2 im ISLR-Buch gibt einen tieferen Einblick in die Thematik Principal Component Analysis by Datamics, 2018
  • 3.
    Übersicht • Lasst unsdie grundsätzliche Idee hinter der PCA (deutsch Hauptkomponentenanalyse) besprechen. • Das mathematische Verfahren ist auch bekannt als Hauptachsentransformation oder Singulärwertzerlegung • Es ist eine „unsupervised“ multivarianten Statistik, um die Beziehung zwischen Variablen eines Datensatzes zu untersuchen. • Sie dient dazu, umfangreiche Datensätze zu strukturieren, zu vereinfachen und zu veranschaulichen • Sie ist auch manchmal als allgemeine Faktor Analyse bekannt. Principal Component Analysis by Datamics, 2018
  • 4.
    Anwendungsbeispiel 1 Bei derBetrachtung von Schiffen wurden die Merkmale Länge, Breite, Wasserverdrängung, Tiefgang, Leistung der Maschinen, Geschwindigkeit (längerfristig mögliche Höchstgeschwindigkeit), erfasst. • Die Merkmale Länge, Breite, Wasserverdrängung und Tiefgang können so aufgefasst werden, dass sie alle einen ähnlichen Sachverhalt messen, den man als den Faktor „Größe“ beschreiben könnte. • Die Leistung der Maschinen und die Höchstgeschwindigkeit könnte zu einem Faktor „Geschwindigkeit“ zusammengefasst werden. Principal Component Analysis by Datamics, 2018
  • 5.
    Anwendungsbeispiel 2 • Beidem Kaufverhalten von Konsumenten, gibt es möglicherweise latente Faktoren wie sozialer Status, Alter oder Familienstand, die bestimmte Käufe motivieren. • Hier könnte man durch gezielte Werbung die “Kauflust” entsprechend kanalisieren. Principal Component Analysis by Datamics, 2018
  • 6.
    Verfahren • Die bereitsbehandelte Regression bestimmt eine Linie, die den gesamten Datensatz bestmöglich repräsentiert. • Die PCA bestimmt mehrere orthogonale Linien, die das selbe tun sollen. • Orthogonal bedeutet „im rechten Winkel“. • Genau genommen sind die Linien senkrecht zueinander im n-dimensionalen Raum. • n-dimensionaler Raum ist der Raum der verschiedenen Variablen • Es gibt so viele Dimensionen wie es Variablen gibt. D.h. in einem Datensatz mit 4 Variablen gibt es auch 4 Dimensionen im Raum. Principal Component Analysis by Datamics, 2018
  • 7.
    Verfahren • Hier sehenwir einige Daten entlang der beiden Features (bzw. Achsen) x und y dargestellt. Principal Component Analysis by Datamics, 2018
  • 8.
    Verfahren • Wir könnenjetzt eine orthogonale Linie hinzufügen. • Jetzt können wir damit beginnen die “Components“ zu verstehen! Principal Component Analysis by Datamics, 2018
  • 9.
    Verfahren • Components sindeine lineare Transformation die ein Variablensystem des Datensatzes wählt, damit folgendes Ziel erfüllt wird: • Der größtmögliche Anteil der Varianz im Datensatz soll durch die erste Achse erklärt werden. Principal Component Analysis by Datamics, 2018
  • 10.
    Verfahren • Der zweitgrößteAnteil der Varianz im Datensatz soll durch die zweite Achse erklärt werden. • Und so weiter... • Dieser Prozess erlaub es uns die Anzahl an Variablen für spätere Analyse zu reduzieren. Principal Component Analysis by Datamics, 2018
  • 11.
    Verfahren • Der zweitgrößteAnteil der Varianz im Datensatz soll durch die zweite Achse erklärt werden. • Und so weiter... • Dieser Prozess erlaub es uns die Anzahl an Variablen für spätere Analyse zu reduzieren. Principal Component Analysis by Datamics, 2018
  • 12.
    Verfahren • Die Componentssind dabei nicht korreliert, da sie im Raum der Samples gegeneinander orthogonal sind. Principal Component Analysis by Datamics, 2018
  • 13.
    Verfahren • Und wirkönnen diesen Prozess auch in höhere Dimensionen fortsetzen. Principal Component Analysis by Datamics, 2018
  • 14.
    Verfahren • Wenn wirdiese Technik jetzt auf einen Datensatz mit eine Vielzahl an Variablen anwenden, dann können wir die erklärte Varianz in einige wenige Components übertragen. • Die größte Herausforderung dabei ist es, die Components richtig zu interpretieren! Principal Component Analysis by Datamics, 2018
  • 15.
    PCA mit Python •Für unsere Anwendung mit Python werden wir uns ein Beispiel einer PCA mit SciKit Learn anschauen. • Wir wollen dafür unsere Daten standardisieren, bevor wir sie in einer PCA verwenden, deshalb behandeln wir diesen Schritt ebenfalls. • Da dieser Algorithmus üblicherweise für Analyse von Daten und nicht für ein voll einsetzbares Modell wird es zu diesem Kapitel kein Portfolio Projekt geben. Principal Component Analysis by Datamics, 2018