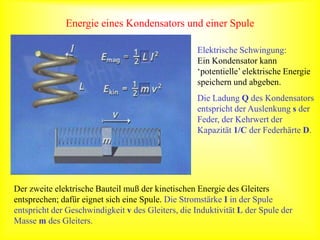
Das Dokument behandelt grundlegende Konzepte und Beispiele für periodische Vorgänge in der Physik, darunter den Tag-Nacht-Zyklus und elektromagnetische Schwingungen in Schaltkreisen. Es erklärt die Umwandlung von potenzieller in kinetische Energie anhand von Federpendeln und elektrischen Bauteilen wie Kondensatoren und Spulen. Zudem werden Formeln zur Berechnung der Frequenz und der Periodendauer vorgestellt, sowie deren Anwendung bei elektrischen Schwingkreisen.