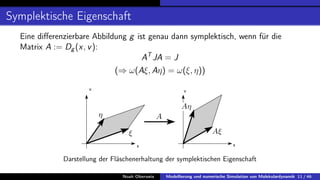
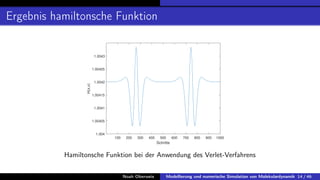
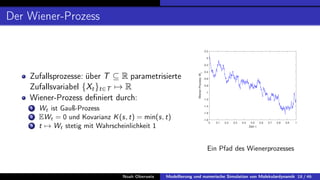
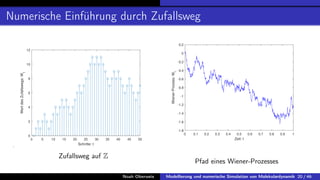
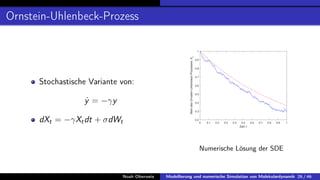
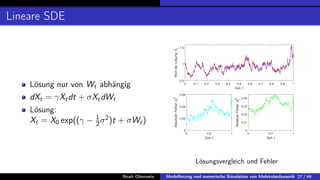
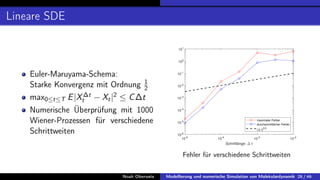
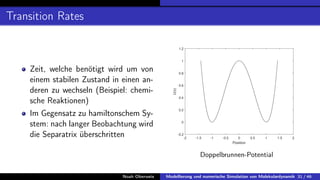
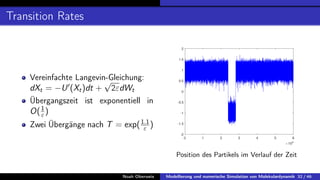
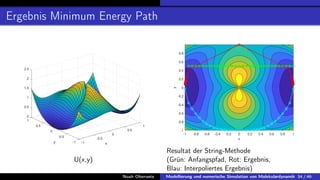
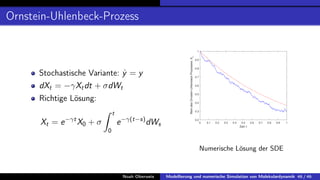
In der Bachelorarbeit von Noah Oberweis wird die Modellierung und numerische Simulation von Molekulardynamik behandelt, mit einem Schwerpunkt auf Hamiltonsche Systeme und stochastische Differentialgleichungen. Die Arbeit umfasst die Entwicklung und Implementierung numerischer Methoden wie das Euler-Maruyama-Verfahren und beschäftigt sich mit seltenen Ereignissen in der Molekulardynamik, insbesondere in Bezug auf Übergangszeiten und Minimale Energiepfade. Ein besonderes Augenmerk liegt auf der Analyse der Langevin-Gleichung und deren Anwendung auf die Simulation von biologischen Prozessen wie der Proteinfaltung.