Downloaden Sie, um offline zu lesen
![Entropie
15
− "
#$%
&
'# log '#
log + = − log '
Gleichverteilung Keine Gleichverteilung
'%, '., … , '& ist ein stochastischer Vektor, d.h.,
• '%, '., … '& ∈ [0,1] und
• ∑'# = 1
Nichts Neues: Shannon (1948)](https://image.slidesharecdn.com/representation-learning-mmohr-26-190329094651/85/Representation-Learning-von-Zeitreihen-15-320.jpg)
Hochgeladen voninovex GmbH
Representation Learning von Zeitreihen
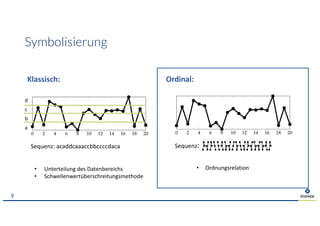
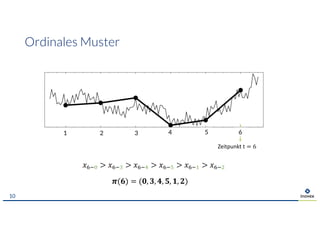
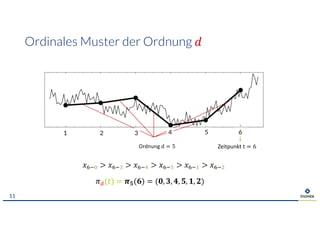
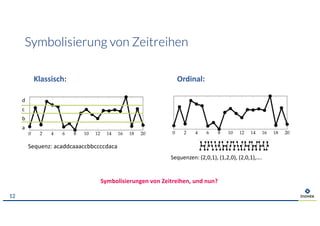
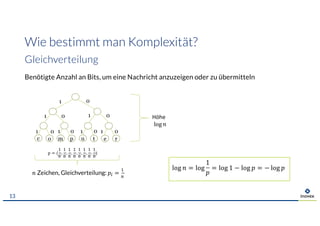
Das Dokument behandelt das Thema der Vorhersage von Zeitreihen durch Representation Learning, wobei der Fokus auf den Ergebnissen des M4-Wettbewerbs liegt, der die Wirksamkeit statistischer und maschineller Lernmethoden vergleicht. Es wird die Herausforderungen und Grenzen von Deep Learning diskutiert, insbesondere im Hinblick auf Datenbedarf und Transferfähigkeit. Zudem wird Permutationsentropie als Maß für die Analyse von Zeitreihen vorgestellt, mit Anwendungen in verschiedenen Bereichen wie Medizin und Finanzwesen.
Representation Learning von Zeitreihen
- 1. Das Unvorhersehbare vorhersagen: RepresentationLearning von Zeitreihen Marisa Mohr Köln, 26. März 2019
- 2. M.Sc. Mathematik Machine LearningEngineer @inovex • Machine Perception & Artificial Intelligence Doktorandin @Universität zu Lübeck • Institut für Informationssysteme, Prof. Dr. Ralf Möller • “Time-Series Representation Learning” Marisa Mohr 2
- 3.
- 4. Makridakis 4 (M4)-Wettbewerb 1.1.2018– 31.5.2018 › 100.000 reale Zeitreihen › „Wie lässt sich die Prognosegenauigkeit für Zeitreihen verbessern und für jeden Fall die am besten geeigneten Methoden ermitteln?“ 4
- 5. Makridakis 4 (M4)-Wettbewerb 1.1.2018– 31.5.2018 Ergebnisse: › 12/17 genauesten Methoden: Kombinationen von überwiegend statistischen Ansätzen › 1. Platz: Hybrider-Ansatz (sowohl Statistik als auch ML) › 2. Platz: Kombination aus 7 statistischen Methoden und 1 ML-Methode › Die 6 reinen ML-Methoden waren alle schlecht › Keiner von ihnen ist genauer als der statistische Benchmark und › nur einer ist genauer als Naive 5
- 6. Deep Learning Ein kritischerBlick Tiefe künstliche neuronale Netze leisten unbestritten Fantastisches! Aber • Daten-hungrig • Beschränkter Transfer: Häufiges Versagen bei Extrapolation • Tiefe Architektur, aber kein tiefes Daten-Verständnis 6 Interesse eines „besseren“ Representation/Feature Learning – vor/innerhalb der eigentlichen Modellierung
- 7. Informations- theoretischer Ansatz • Wie “komplex”ist eine Zeitreihe? • Nutze das „Auf und Ab“ • Inhomogenität, Unreinheit • Unsicherheit, Unvorhersagbarkeit 7
- 8.
- 9. Symbolisierung 9 • Unterteilung desDatenbereichs • Schwellenwertüberschreitungsmethode • Ordnungsrelation d c b a Sequenz: acaddcaaaccbbccccdaca Klassisch: Ordinal: Sequenz:
- 10. Ordinales Muster 10 !(#) =(&, (, ), *, +, ,) -./0 > -./2 > -./3 > -./4 > -./5 > -./6 Zeitpunkt t = 6 1 2 3 4 5 6
- 11. Ordinales Muster derOrdnung ! 11 Zeitpunkt t = 6Ordnung d = 5 1 2 3 4 5 6 '()* > '(), > '()- > '(). > '()/ > '()0 12(4) = 67(8) = (9, ;, <, 7, =, >)
- 12. Symbolisierung von Zeitreihen 12 Klassisch:Ordinal: Symbolisierungen von Zeitreihen, und nun? Sequenzen: (2,0,1), (1,2,0), (2,0,1),…. d c b a Sequenz: acaddcaaaccbbccccdaca
- 13. Benötigte Anzahl anBits, um eine Nachricht anzuzeigen oder zu übermitteln Wie bestimmt man Komplexität? Gleichverteilung 13 c o m p u t e r 1 1 1 1 1 1 1 0 0 0 0 0 0 0 ! Zeichen, Gleichverteilung: "# = % & p = ( 1 8 , 1 8 , 1 8 , 1 8 , 1 8 , 1 8 , 1 8 , 1 8 ) Höhe log ! log ! = log 1 " = log 1 − log " = − log "
- 14. › Nicht jedesZeichen bzw. jede Nachricht ist gleichverteilt › Sequenz: acaddcaaaccbbccccdaca Wie bestimmt man Komplexität? Keine Gleichverteilung 14 b d 1 1 1 0 0 0 p = ( 2 21 , 3 21 , 7 21 , 9 21 ) a c + Zeichen, keine Gleichverteilung: ,- ≠ ,/ Nachrich t Code Länge Erwartet e Länge b 111 3 0,286 d 110 3 0,429 a 10 2 0,667 c 0 1 0,429 Erwartete Länge 1,811
- 15. Entropie 15 − " #$% & '# log'# log + = − log ' Gleichverteilung Keine Gleichverteilung '%, '., … , '& ist ein stochastischer Vektor, d.h., • '%, '., … '& ∈ [0,1] und • ∑'# = 1 Nichts Neues: Shannon (1948)
- 16. = Shannon-Entropie ordinalerMuster wobei ! " die relative Häufigkeit des ordinalen Musters " in der Zeitreihe ist. 16 Permutationsentropie (PE) − $ %∈' ! " log ! " ,
- 17. Beispiel 17 !"# = − 4 5 log 4 5 − 1 5 log 1 5 ≈0,7219 • 4 Paare mit 23 < 235#, d.h., 6# 78 = (0,1) • 1 Paare mit 23 > 235#, d.h., 6# 78 = (1,0) 1 2 3 4 5 6
- 18. PE im DeepLearning Nur ein weiteres beschreibendes Maß? • Strukturen von Daten lernen • PE „natürliches, intrinsisches“ Maß basierend auf Informationen • Auf und Ab des erzeugenden Systems • Konzeptionelles Maß • „Funktioniert“ auch bei chaotischen Systemen 18
- 19.
- 20. Datensätze 20 Theoretische Systeme • Lorenz- und RösslerSystem • Henon-Map • Logistische Gleichung • Bernoulli-Shift • Brown’sche Bewegung • Gauß’sches Rauschen • … Signale • Sprachsignale • Chaotische Signale • … Physikalische Systeme • Opto- elektronische Oszillatoren • Viele Arten von Lasern • … Medizin • epileptische Aktivität in EEG-Daten • Lokale Feldpotenziale • EKG-Daten • … Wirtschaft und Umwelt • Rekrutierung von Fischen • Population kanadischer Luchs • Sedimentdaten • Anleihen- Indizes und Aktien • Dow-Jones- Subindizes • …
- 21. Quelle: Keller, K.,Mangold, T., Stolz, I., Werner, J.: Permutation Entropy: New Ideas and Challenges Entropy 19(3) (2017) Klassifikation von EEG Daten 21 Daten: • EEG-Datenbank • Länge von 23.6s • Sampling Rate 173.61 Hz. • 5 Gruppen, je 100 Zeitreihen Gesund? Wie gemessen? Zustand A ja Oberfläche Offene Augen B ja Oberfläche Geschlossene Augen C nein Intrakraniell, epileptogene Zone Anfallsfreie Zeit D nein Intrakraniell, gegenüberliegende Gehirnhälfte Anfallsfreie Zeit E nein intrakraniell Anfallszeit
- 22. Quelle: Keller, K.,Mangold, T., Stolz, I., Werner, J.: Permutation Entropy: New Ideas and Challenges Entropy 19(3) (2017) Klassifikation von EEG Daten 22
- 23. Quelle: Keller, K.,Mangold, T., Stolz, I., Werner, J.: Permutation Entropy: New Ideas and Challenges Entropy 19(3) (2017) Klassifikation von EEG Daten 23 Ziel: Klassifikation von EEG-Daten zur Epilepsie-Detektion unter Verwendung von PE (sowie Erweiterungen) Modell: Random Forest Accuracy: bis zu 71,8%
- 24. https://www.cmsattler.de/diktieren-spracherkennung-und-sprache-4-0/ , http://truth-and-beauty.net/projects/emoto,https://medium.com/@5agado/building-a-personal-virtual- assistant-step-1-your-cv-as-a-chatbot-a4381fce6983 Weitere sequentielle Daten 24
- 25. Vielen Dank Marisa Mohr MachineLearning Engineer inovex GmbH Friesenweg 4 / Haus 13 22763 Hamburg marisa.mohr@inovex.de 01523 3181 259