Das Dokument behandelt das Thema der Blockmodellierung in Netzwerken und erläutert die reguläre Äquivalenz von Knoten in Graphen. Es werden Methoden zur exakten Bestimmung der maximalen regulären Äquivalenz vorgestellt, darunter der Catreg-Algorithmus, sowie dessen Laufzeitkomplexität. Beispiele veranschaulichen die Iterationsschritte und die Berechnung der Nachbarschaftsmengen in Bezug auf unterschiedliche Äquivalenzklassen.






![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
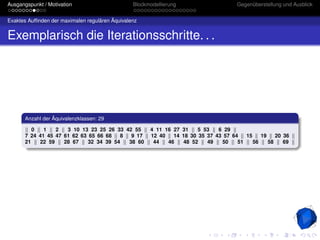
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-7-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-8-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-9-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-10-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-11-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-12-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-13-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-14-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Der CATREGE-Algorithmus [Borgatti u. Everett, 1993]
Sei P die jeweils aktuelle Partition des Graphen.
1 Starte P mit allen Knoten in ein und derselben Äquivalenzklasse.
Anmerkung: Natürlich sind alternative Vorgaben für P möglich.
2 Für jeden Knoten berechne dessen Nachbarschaftsmenge bezüglich P neu.
3 Für jedes Paar von Knoten vergleiche deren Nachbarschaftsmengen:
→ Übereinstimmung: Knoten bleiben äquivalent.
→ Abweichung: Eröffne neue Äquivalenzklasse für einen der Knoten.
4 Wiederhole ab (2) solange Veränderungen eingetreten sind.
5 Gebe Partition P als Lösung zurück.](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-15-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Eigenschaften
Terminiert mit dem sog. Regular Interior [Borgatti und Everett]
d.h. der maximalen regulären Partion P ≤ der Startpartition.
Laufzeit O(n3 )
maximal n Iterationen, da Anzahl der Äquivalenzklassen
streng monoton steigend – bis auf den letzten Schritt.
Laufzeit eines Schritts beträgt O( n(n−1) ) = O(n2 ).
2
Prädestiniert für Umgang mit Multiplen Relationen
über stets separate Bestimmung der Nachbarschaftsmengen
Implementierung
nicht mehr als 300-400 Zeilen Quellcode in C++](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-16-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Eigenschaften
Terminiert mit dem sog. Regular Interior [Borgatti und Everett]
d.h. der maximalen regulären Partion P ≤ der Startpartition.
Laufzeit O(n3 )
maximal n Iterationen, da Anzahl der Äquivalenzklassen
streng monoton steigend – bis auf den letzten Schritt.
Laufzeit eines Schritts beträgt O( n(n−1) ) = O(n2 ).
2
Prädestiniert für Umgang mit Multiplen Relationen
über stets separate Bestimmung der Nachbarschaftsmengen
Implementierung
nicht mehr als 300-400 Zeilen Quellcode in C++](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-17-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Eigenschaften
Terminiert mit dem sog. Regular Interior [Borgatti und Everett]
d.h. der maximalen regulären Partion P ≤ der Startpartition.
Laufzeit O(n3 )
maximal n Iterationen, da Anzahl der Äquivalenzklassen
streng monoton steigend – bis auf den letzten Schritt.
Laufzeit eines Schritts beträgt O( n(n−1) ) = O(n2 ).
2
Prädestiniert für Umgang mit Multiplen Relationen
über stets separate Bestimmung der Nachbarschaftsmengen
Implementierung
nicht mehr als 300-400 Zeilen Quellcode in C++](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-18-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Eigenschaften
Terminiert mit dem sog. Regular Interior [Borgatti und Everett]
d.h. der maximalen regulären Partion P ≤ der Startpartition.
Laufzeit O(n3 )
maximal n Iterationen, da Anzahl der Äquivalenzklassen
streng monoton steigend – bis auf den letzten Schritt.
Laufzeit eines Schritts beträgt O( n(n−1) ) = O(n2 ).
2
Prädestiniert für Umgang mit Multiplen Relationen
über stets separate Bestimmung der Nachbarschaftsmengen
Implementierung
nicht mehr als 300-400 Zeilen Quellcode in C++](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-19-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
Exaktes Auffinden der maximalen regulären Äquivalenz
Beispiel: Geschäftsbeziehungen von 70 Fotografen
Wer beliefert wen? [weitgehende Planardarstellung mit Social Network Visualizer SocNetV]
10
24
57 68 55
44
48 69
26
8 63
67 50
40
51
61
2
29
13
28 39 25
64 60 4 47 17
46 21 53
37 1 70
54 31
52 20 56
30 59 27 16
38 58
35
6 19
45 43
33 15 5
22 32 18 14
34
9
62
66
36 23 42
49
65
3 11
7
12 41](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-20-320.jpg)















































![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
IP-Formulierung
IP-Formulierung [Brusco, Steinley]
N N N N
min pkl yijkl sij + pkl αikl + pkl β
i=1 j=1 (k ,l)|bkl =0 i=1 (k ,l)|bkl =1 j=1 (k ,l)|bkl =1
K N
s.t. xik = 1 xik ≥ 1 (1)
k =1 i=1
xik + xjl − yijkl ≤ 1 xik + xjl − 2 yijkl ≥ 0 (2)
N N
yijkl sij + αikl ≥ xik yijkl sij + βjkl ≥ xjl (3)
j=1 i=1
xik , yijkl ∈ {0, 1} αikl , βjkl ∈ {0, 1} (4)](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-69-320.jpg)
![Ausgangspunkt / Motivation Blockmodellierung Gegenüberstellung und Ausblick
IP-Formulierung
IP-Formulierung [äquivalent und lesbar]
K K N N N N
min pkl ¬bkl yijkl sij + bkl αikl + βjkl
k =1 l=1 i=1 j=1 i=1 j=1
K N
s.t. xik = 1 xik ≥ 1 (1)
k =1 i=1
xik + xjl − yijkl ≤ 1 xik + xjl − 2 yijkl ≥ 0 (2)
N N
yijkl sij + αikl ≥ xik yijkl sij + βjkl ≥ xjl (3)
j=1 i=1
xik , yijkl ∈ {0, 1} αikl , βjkl ∈ {0, 1} (4)](https://image.slidesharecdn.com/vortrag-120625081613-phpapp02/85/Regulare-Aquivalenz-IP-Formulierung-von-Blockmodellen-70-320.jpg)









