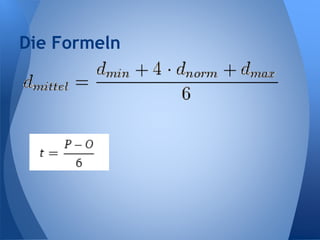
Die US-Armee hat die Entwicklung einer neuen Rakete mit einer Reichweite von mindestens 3000 km in Auftrag gegeben, die unter Wasser abgefeuert werden kann und einen atomaren Sprengkopf erhalten soll. Um die Entwicklungszeit und -kosten zu schätzen, wird die PERT-Methode verwendet, die eine signifikante Verkürzung der Projektlaufzeit um 45% verspricht. Das Dokument enthält Beispiele und Berechnungen zur Ermittlung der mittleren Dauer und Standardabweichung für verschiedene Aufgaben, um fundierte Zeitpläne zu erstellen.

1. Zeitplanung mit PERT
Program Evaluation and Review
Technique

2. Die US-Armee beauftragt Sie, eine neue
Rakete zu bauen, welche
● Eine Reichweite von mind. 3000km hat
● Unter Wasser abgefeuert werden kann
● Mit einem atomaren Sprengkopf bestückt
ist
● Welchen Sie ebenfalls noch entwickeln
müssen.
Die Entwicklung: 1956

3. Forschung, Entwicklung und Fertigung
müssen an Drittfirmen abgegeben werden.
Niemand hat so etwas bisher gebaut, oder
kann auch nur annähernd schätzen, wie
lange das dauern wird, und wie viel das
kostet.
Das Problem

4. Der Zeitbedarf für jede Aktion wird
geschätzt. Mittels statistischer Formeln
wird dann die grösste Wahrscheinlichkeit
ausgerechnet.
Es wird geschätzt, dass durch diese
Methode die Rakete 45% früher fertig
gestellt werden konnte, als ohne sie.
Die Lösung:

5. Der Aufwand für ein neues Projekt muss
geschätzt werden.
Nun werden folgende drei Szenarien
geschätzt:
● Der allerbeste Fall (p<1%)
● Der wahrscheinlichste Fall
● Der allerschlimmste Fall (p<1%)
Das Konzept

6. Die Formeln

7. Bester Fall: 1 Tag
Wahrscheinlichster Fall: 3 Tage
Schlimmster Fall: 12 Tage
Ein Beispiel

8. dmittel = (1 Tag + 4*3 Tage + 12 Tage)/6
dmittel = 4.2 Tage
Standardabweichung:
𝝈 = (12 Tage - 1 Tag) / 6
𝝈 = 1.8 Tage
In unserem Fall

9. Aufgaben lassen sich zu Sequenzen
verbinden. Dabei gilt:
µSequenz = ΣµAufgabe
𝝈 Sequenz = √Σ𝝈 Aufgabe
2 (√a2+b2+c2)
Aufgaben-Sequenzen

10. Wir haben drei Aufgaben:
Noch ein Beispiel
Aufgabe Optimistisch Standard Pessimistisch
Alpha 1 3 12
Beta 1 1.5 14
Gamma 3 6.25 11
Aufgabe Mittlere Dauer Standardabweichung
Alpha 4.2 1.8
Beta 3.5 2.2
Gamma 6.5 1.3

11. Totale Zeit: 4.2 + 3.5 + 6.5 = ~14 Tage
Abweichung: (1.82 + 2.22 + 1.32)1/2 = 3.13
-> Vermutlich 14 Tage,
+-3 Tage mit p=15%, +-6 Tage mit p=2%
Erwartete Zeit
Aufgabe Mittlere Dauer Standardabweichung
Alpha 4.2 1.8
Beta 3.5 2.2
Gamma 6.5 1.3

12. Martin, Robert C.
Clean Coder
Mehr Infos und Strategien