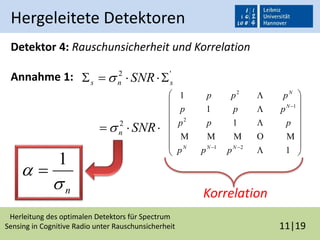
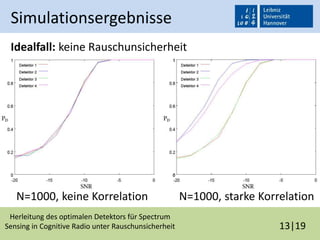
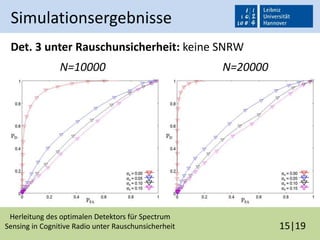
Die Bachelorarbeit von Maxim Penner behandelt die Herleitung des optimalen Detektors für Spectrum Sensing in Cognitive Radio unter Rauschunsicherheit. Es werden verschiedene Detektoren vorgestellt und deren Leistungsfähigkeit in Bezug auf Rauschunsicherheit und Korrelation untersucht, wobei Simulationen und Messergebnisse die Theorien bestätigen. Das Fazit hebt hervor, dass die Einbeziehung von Korrelation die Leistung der Detektoren verbessert, jedoch mit einem hohen Rechenaufwand verbunden ist.







![Herleitung des optimalen Detektors für Spectrum
Sensing in Cognitive Radio unter Rauschunsicherheit 5|19
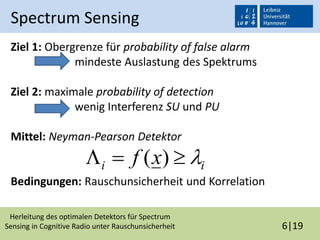
Spectrum Sensing
Hypothese H0: x[k] = w[k]
Hypothese H1: x[k] = w[k] + s[k]](https://image.slidesharecdn.com/kolloqium-140723025827-phpapp01/85/Herleitung-des-optimalen-Detektors-fur-Spectrum-Sensing-in-Cognitive-Radio-unter-Rauschunsicherheit-8-320.jpg)
![Herleitung des optimalen Detektors für Spectrum
Sensing in Cognitive Radio unter Rauschunsicherheit 5|19
Spectrum Sensing
Hypothese H0: x[k] = w[k]
Hypothese H1: x[k] = w[k] + s[k]](https://image.slidesharecdn.com/kolloqium-140723025827-phpapp01/85/Herleitung-des-optimalen-Detektors-fur-Spectrum-Sensing-in-Cognitive-Radio-unter-Rauschunsicherheit-9-320.jpg)