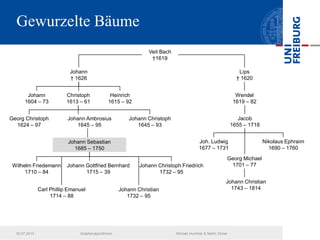
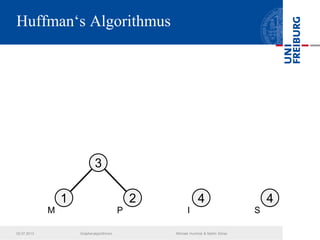
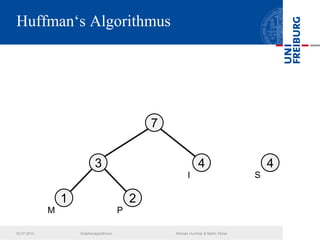
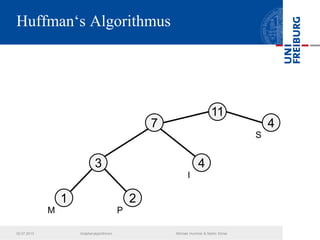
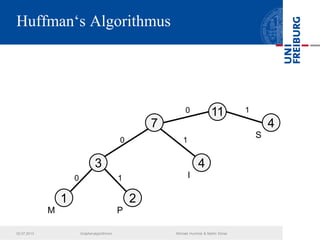
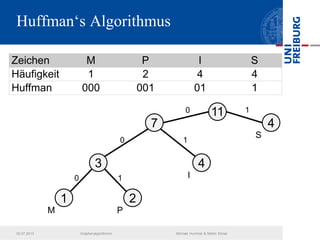
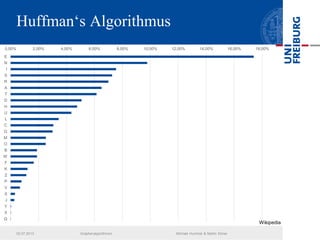
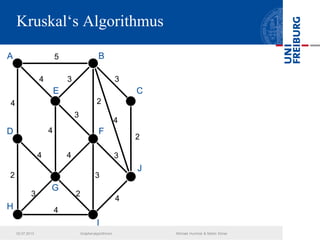
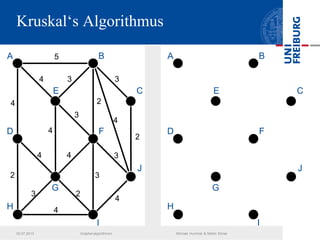
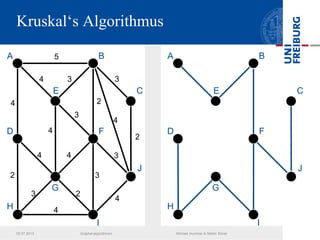
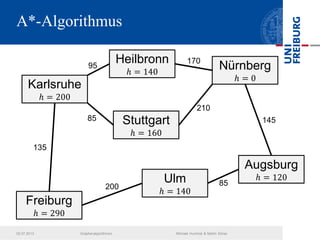
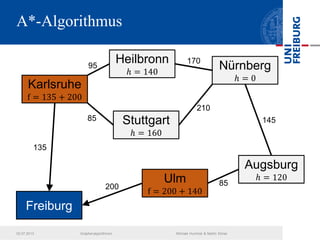
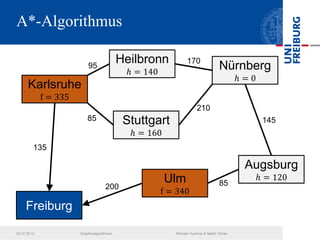
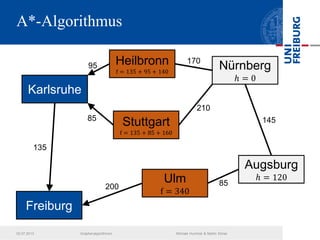
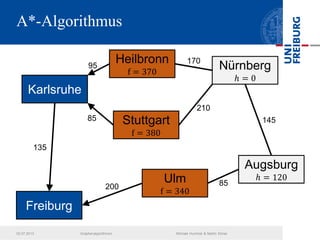
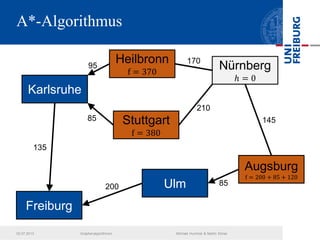
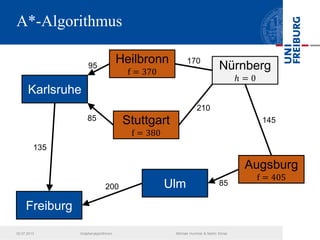
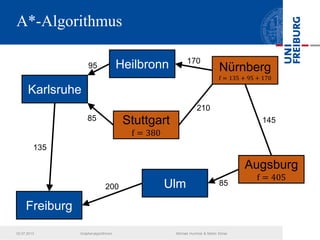
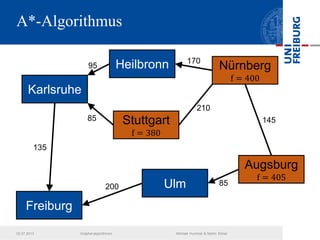
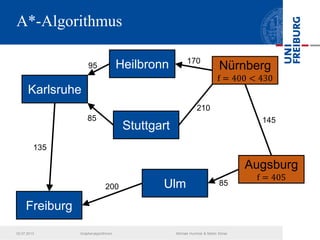
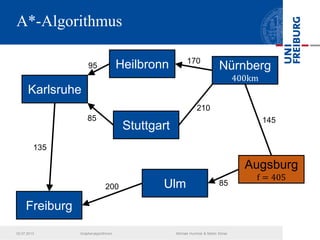
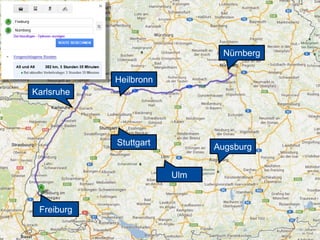
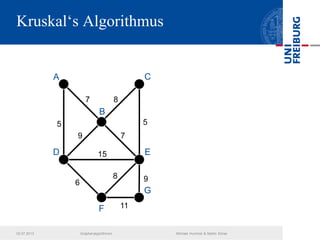
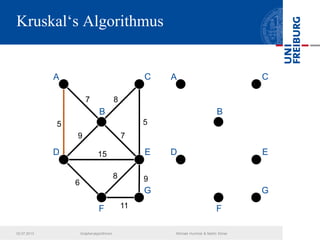
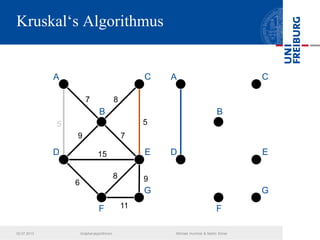
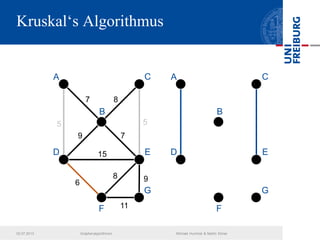
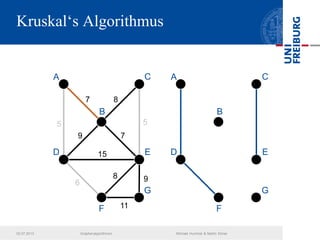
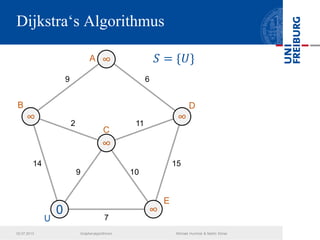
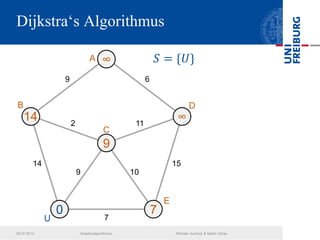
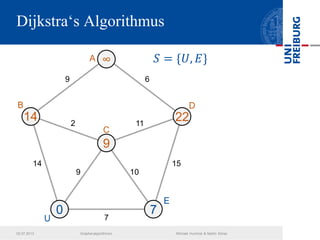
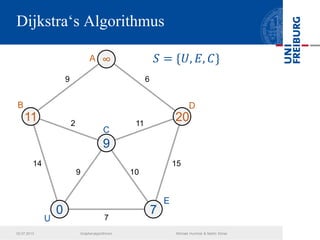
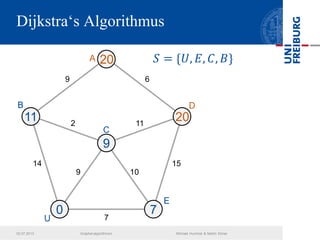
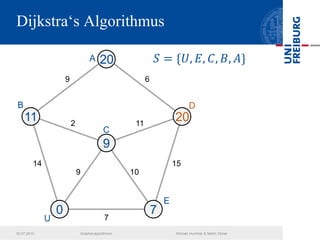
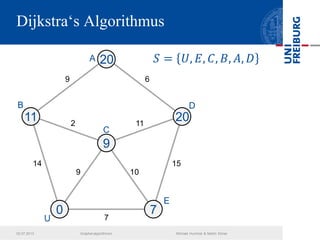
Das Dokument behandelt verschiedene Graphenalgorithmen wie Kruskal's Algorithmus, Dijkstra's Algorithmus und Huffman-Codierung. Es werden spezifische Anwendungsbeispiele und Berechnungen in Bezug auf diese Algorithmen dargestellt. Zudem werden statistische Daten zur Internet-Bandbreite in verschiedenen Regionen präsentiert.







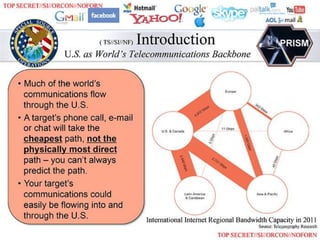
![U.S &
Kanada
Europa
Afrika
Asien &
Pazifik
& Karibik
Lateinamerika
4‘972 343
40
11
1‘345
2‘721
5
2‘946
Bandwidth 2011
[Gbps]
Internet
02.07.2013 Graphenalgorithmen Michael Hummel & Martin Ebner
Telegeography Research](https://image.slidesharecdn.com/graphenalgorithmencd-140317112353-phpapp01/85/Graphenalgorithmen-cd-23-320.jpg)