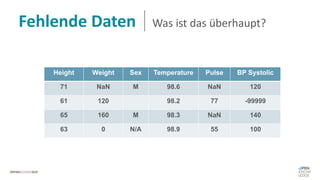
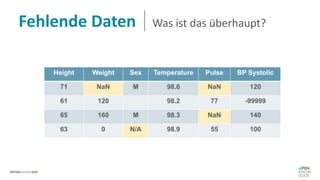
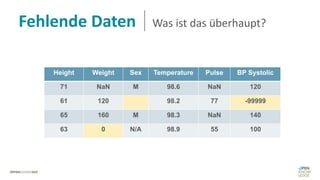
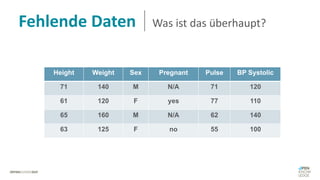
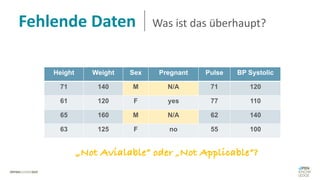
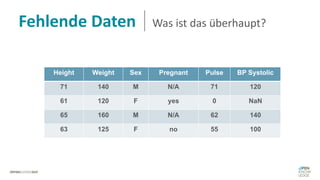
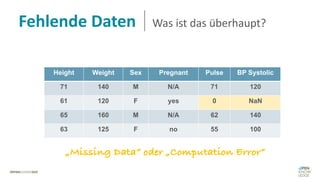
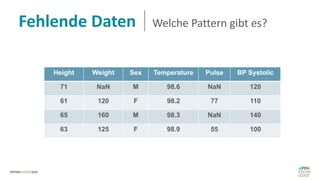
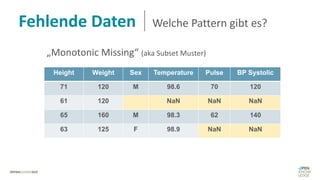
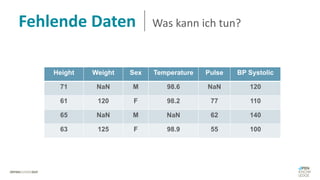
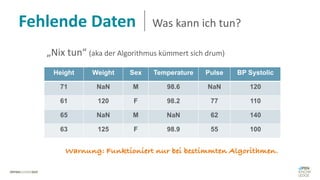
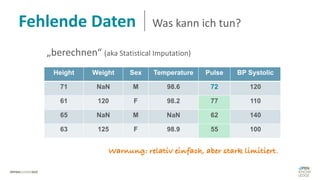
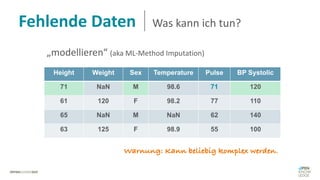
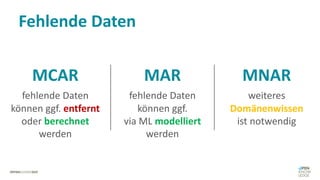
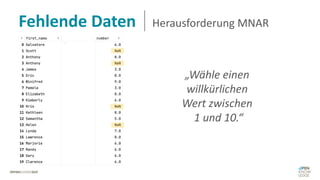
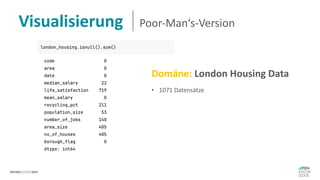
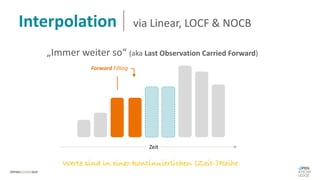
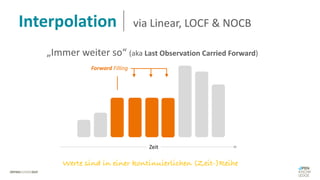
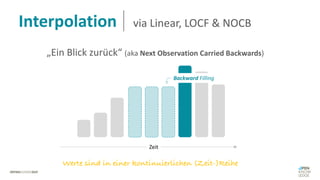
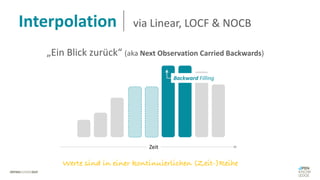
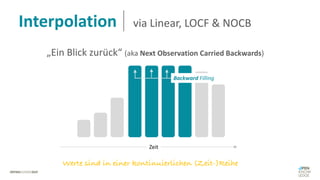
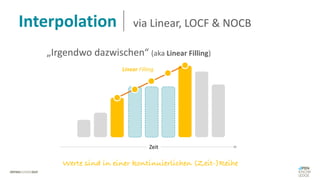
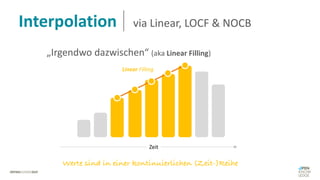
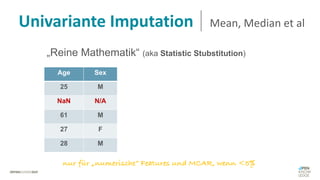
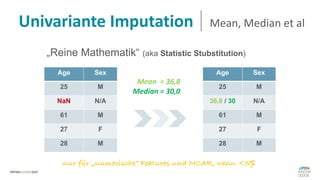
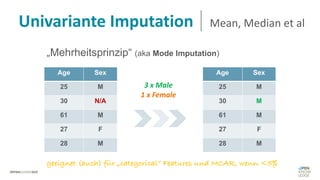
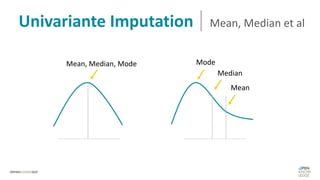
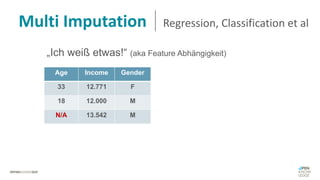
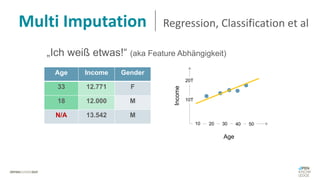
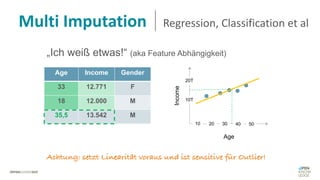
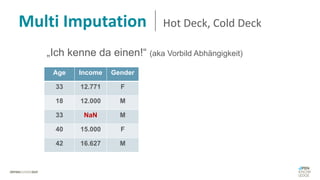
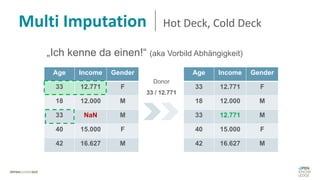
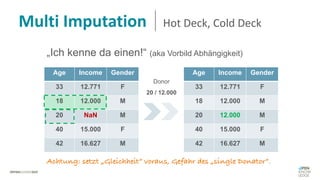
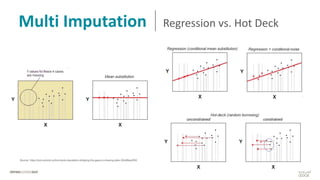
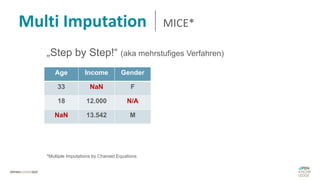
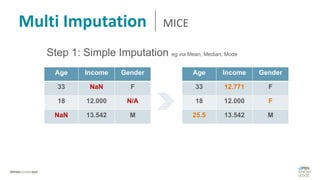
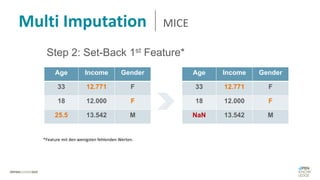
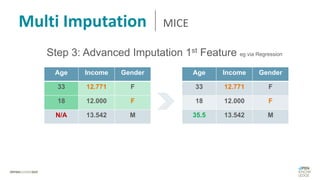
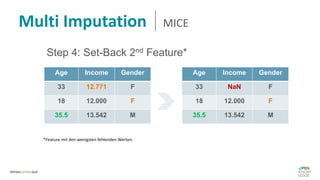
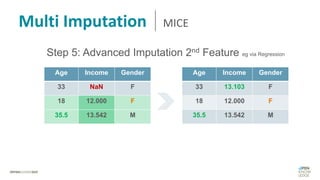
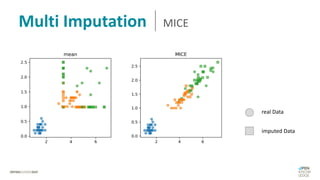
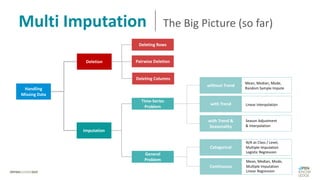
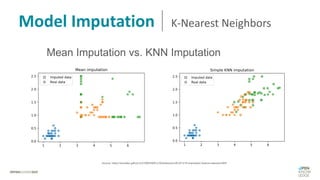
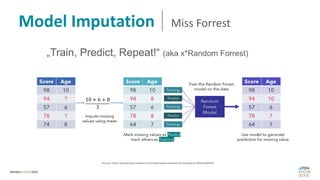
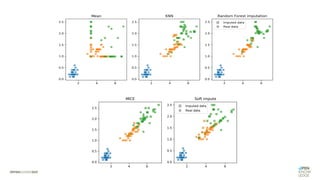
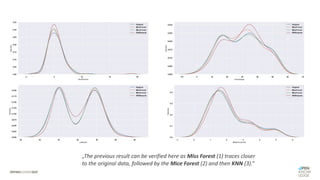
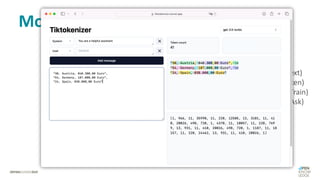
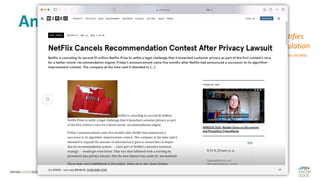
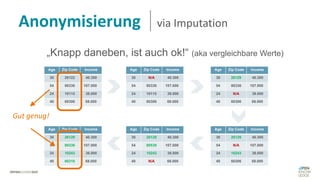
Das Dokument behandelt das Thema fehlende Daten in Datensätzen und deren Imputation. Es erläutert verschiedene Arten und Muster fehlender Daten sowie Methoden zur Imputation, einschließlich univariater und multivariater Ansätze. Relevant sind auch die Herausforderungen bei der Arbeit mit nicht zufällig fehlenden Daten (MNAR) und die Notwendigkeit von Domänenwissen für deren Handhabung.