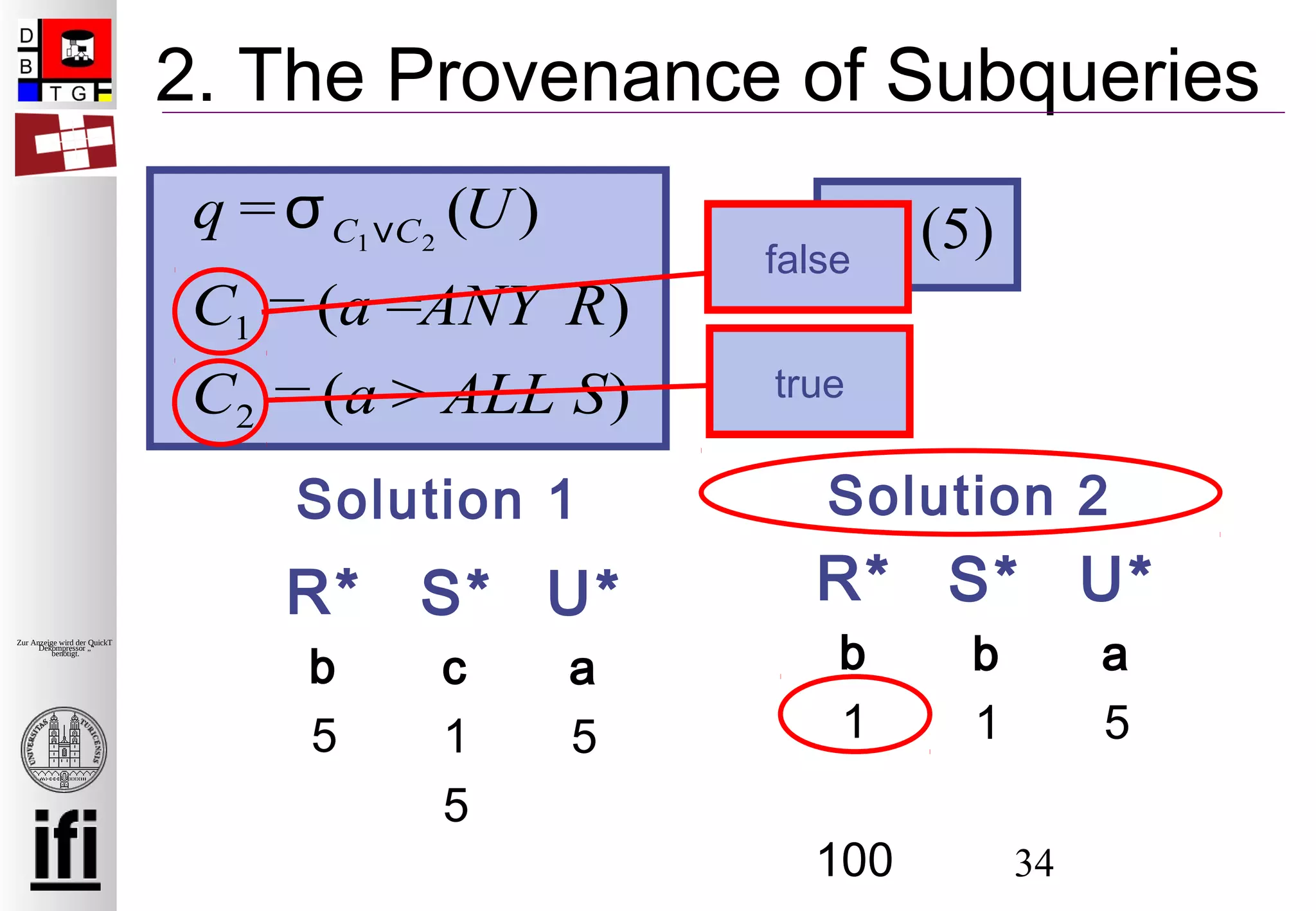
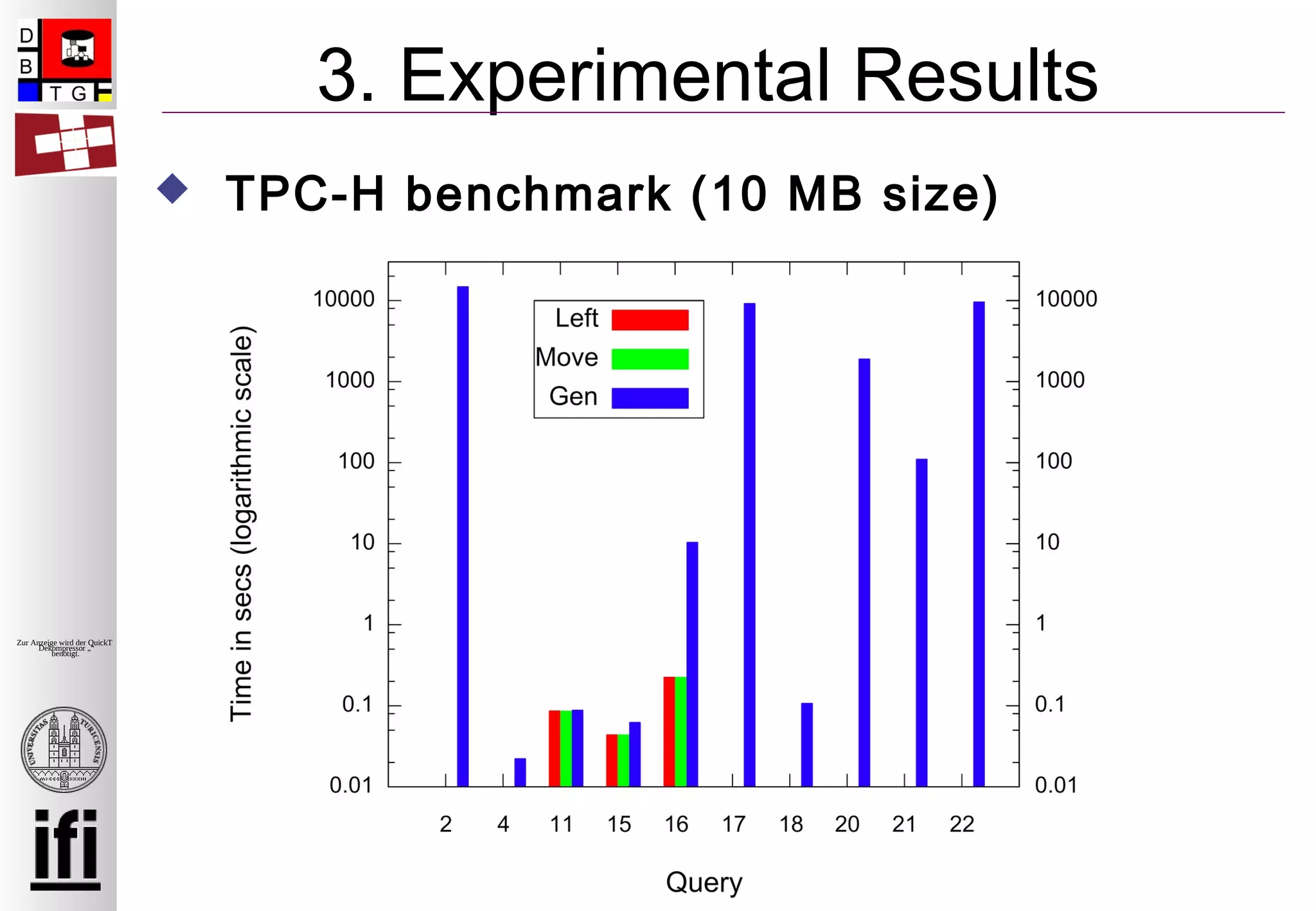
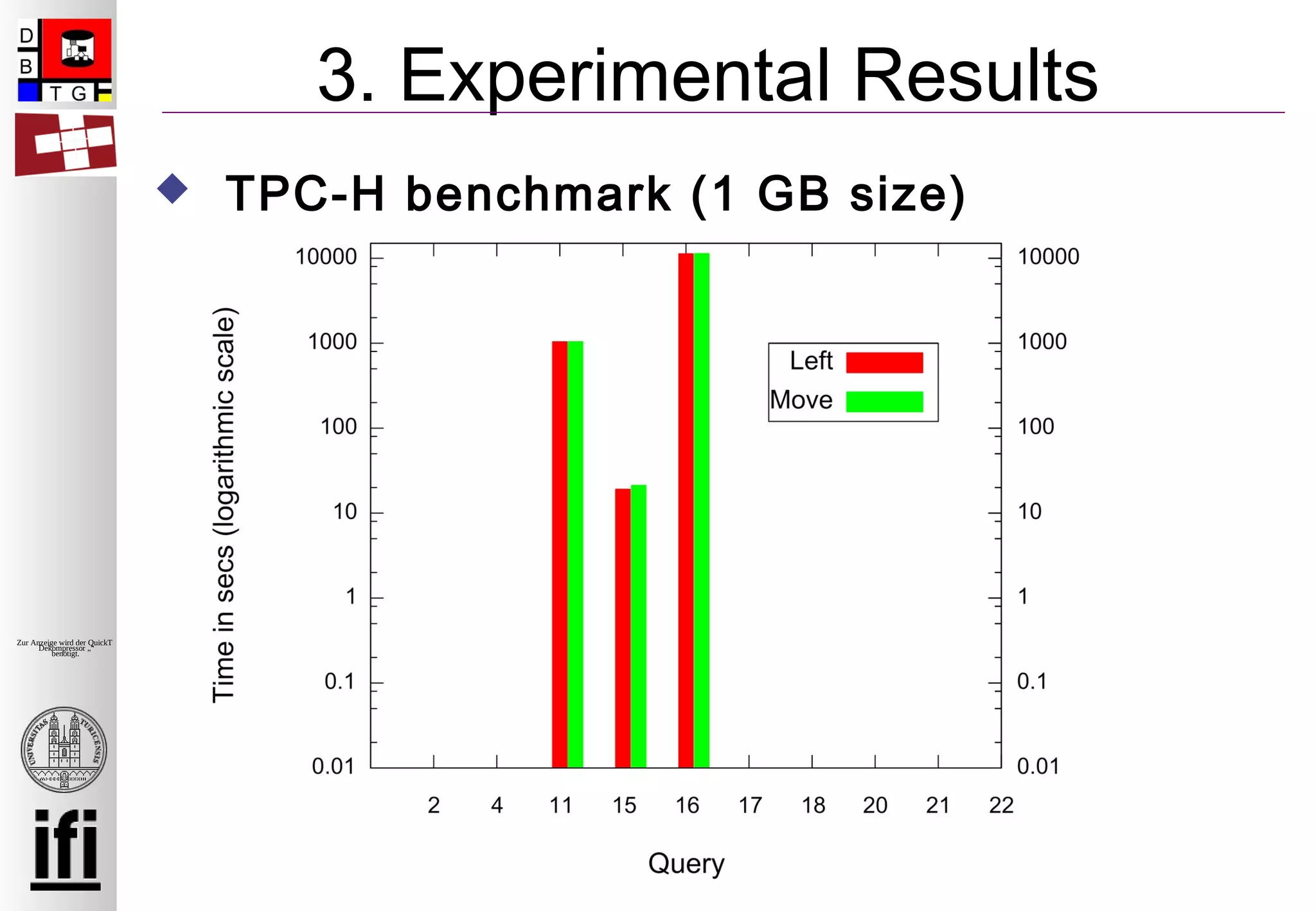
Das Dokument behandelt die Provenienz von verschachtelten Unterabfragen in Datenbanksystemen, insbesondere die Herausforderungen und Lösungsansätze zur Erfassung und Berechnung dieser Provenienz. Es wird eine erweiterte Definition der Provenienz für Unterabfragen vorgeschlagen sowie algorithmische Ansätze zur Implementierung in ein Provenienzmanagementsystem (PERM) diskutiert. Die experimentellen Ergebnisse basieren auf Benchmark-Tests und demonstrieren die Effizienz der vorgeschlagenen Methoden.





![7
Zur Anzeige wird der QuickTime™
Dekompressor „“
benötigt.
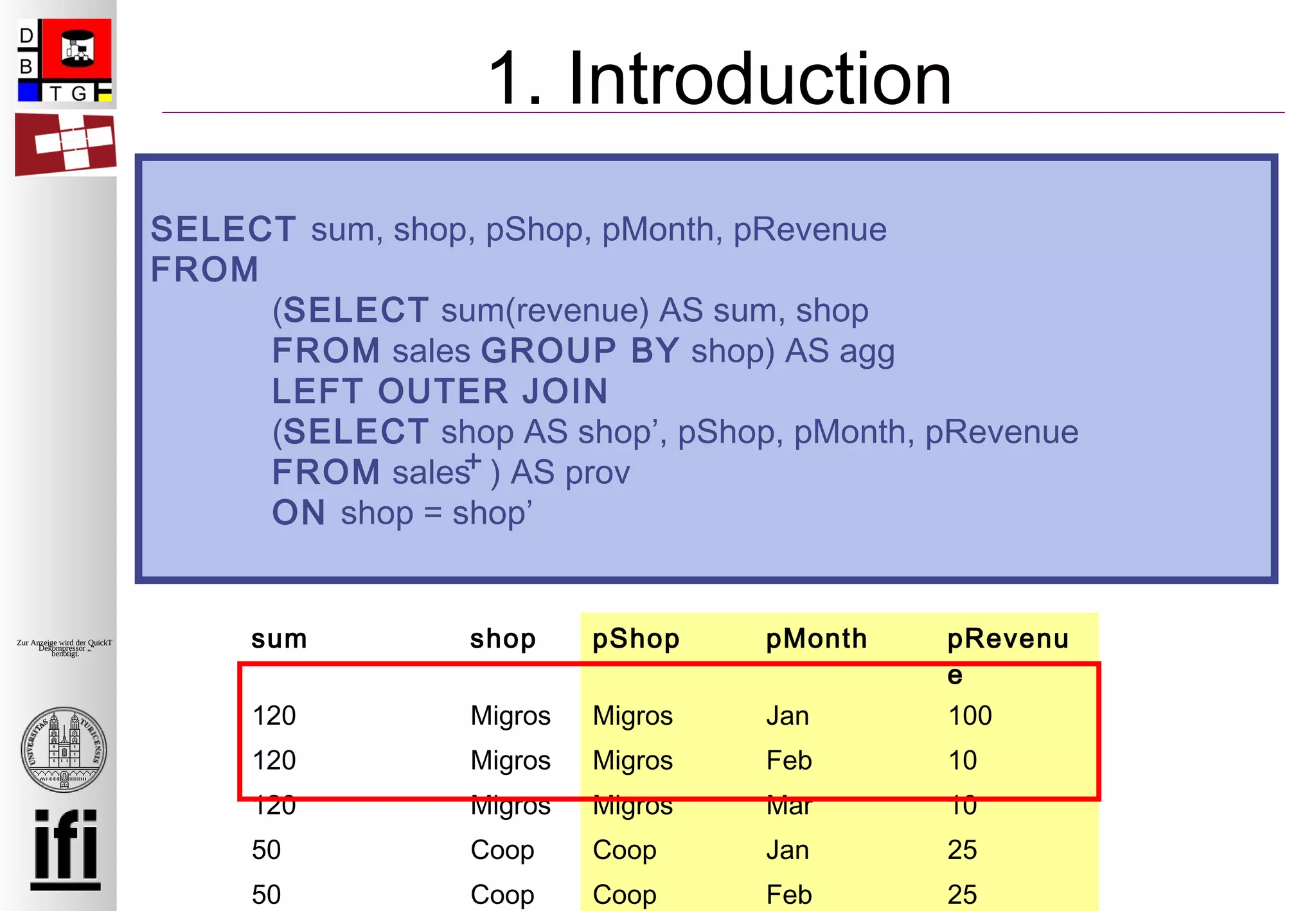
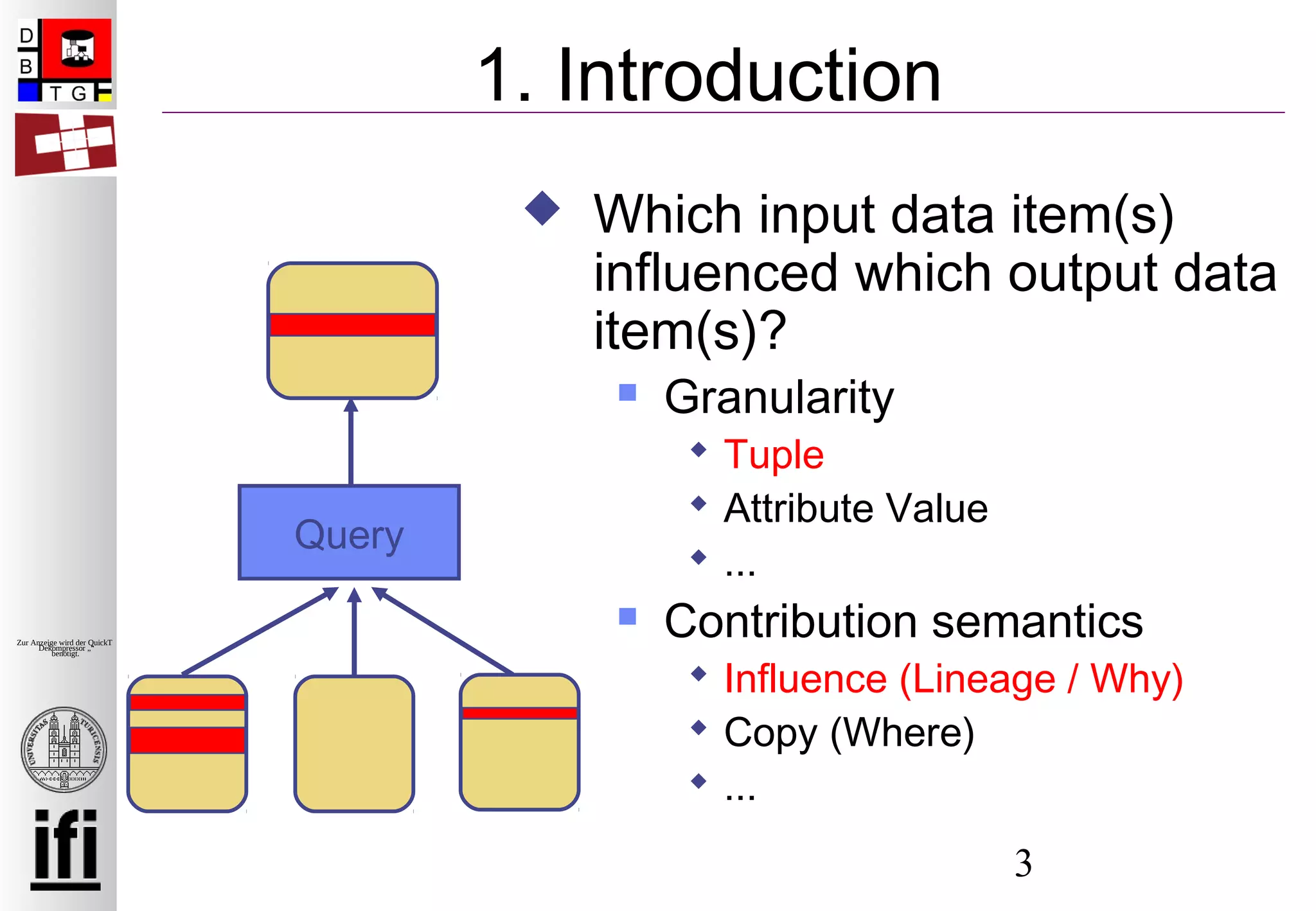
1. Introduction
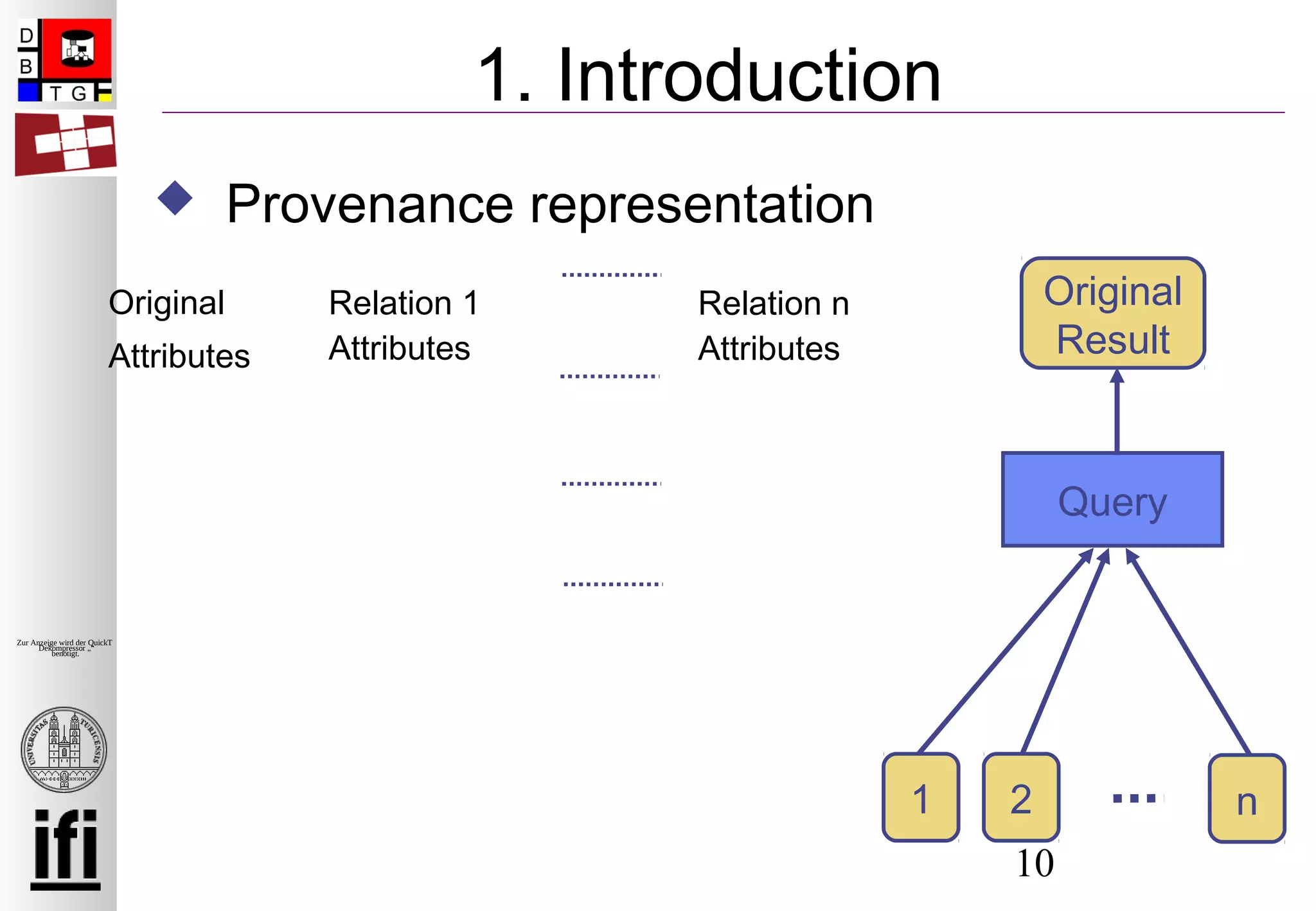
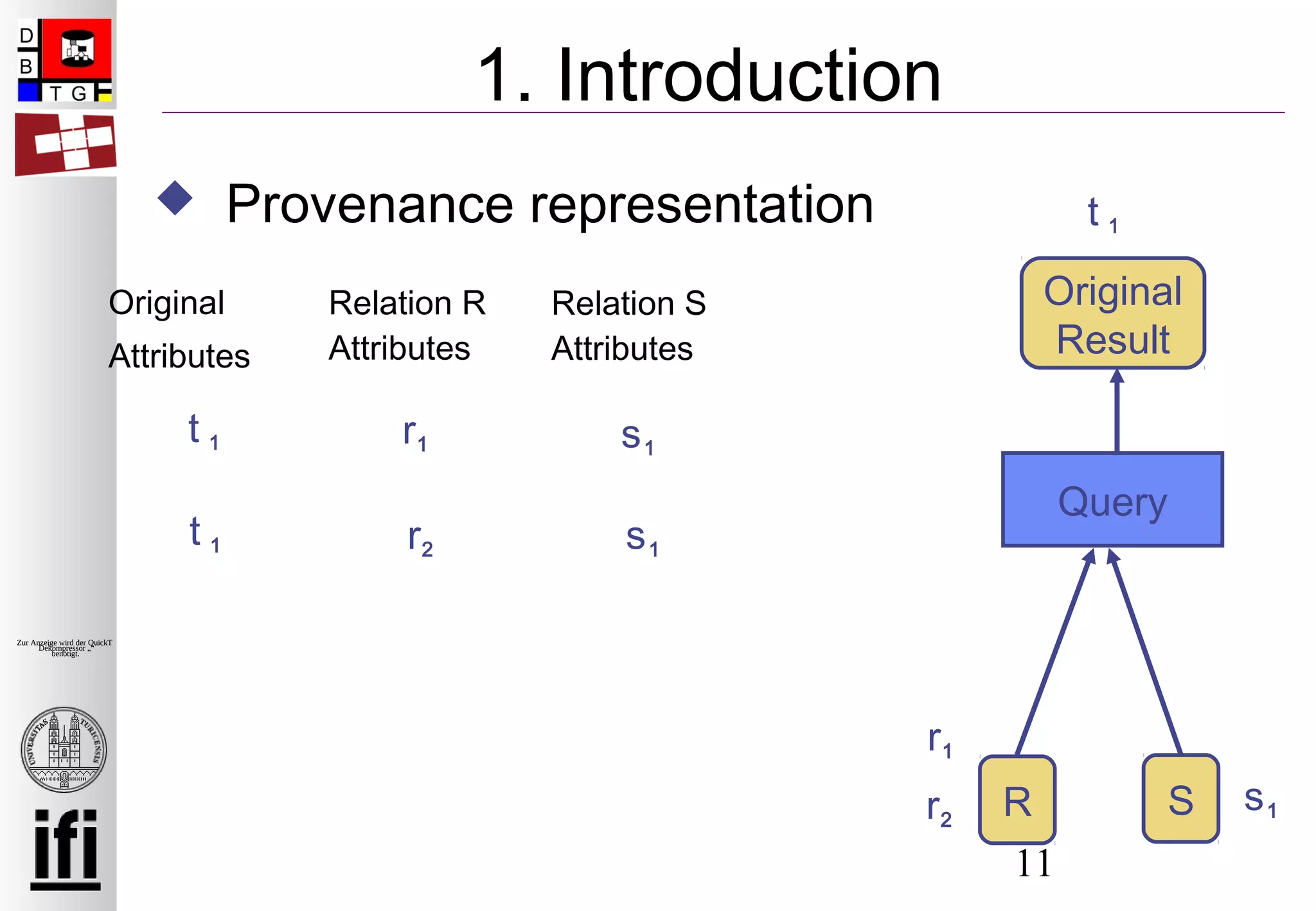
Definition of contribution semantics
Why/Influence-provenance
Introduced in [Cui, Widom ICDE ‘00]
Provenance represented as list of subsets of
the input relations
Defined for a single algebra operator and a
single result tuple](https://image.slidesharecdn.com/2009edbtsublinks-140625071819-phpapp02/75/EDBT-2009-Provenance-for-Nested-Subqueries-7-2048.jpg)