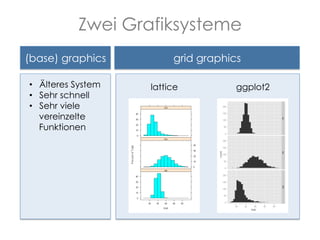
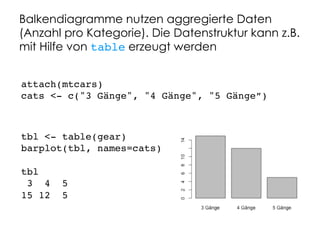
Das Dokument behandelt die verschiedenen Grafiksysteme in R, insbesondere 'base graphics' und 'grid graphics'. Es beschreibt Funktionen zur Erstellung komplexer Grafiken und die Bedeutung von grafischen Parametern, um die Darstellung zu optimieren. Zudem werden einige spezifische Anwendungen und Beispiele für Histogramme und Streudiagramme gegeben, und es wird erläutert, wie man Grafiken in Dateien speichert.




![Don‘t get fooled by default looks: Mit R base graphics
kann man wunderschöne Grafiken produzieren.
Allerdings benötigt dies meist viel Code
!
par(mai=c(0.5,1,0.5,0.5),!
omi=c(0.5,0.5,0.5,0.5),!
family="Lato Light",las=1)!
frauen <- read.csv("daten/frauen.txt",header =F,sep=",")!
for(i in 1:111) !
colnames(frauen)[i]<-paste("x",i+1949,sep="") !
maenner<-read.csv("daten/maenner.txt",header =F,sep=",")!
for(i in 1:111) !
colnames(maenner)[i]<-paste("x",i+1949,sep="")!
rechts<-frauen$x2010!
links<-maenner$x2010!
farbe_rechts<-c(!
rep(rgb(210,210,210,maxColorValue=255),15),!
rep(rgb(144,157,172,maxColorValue=255),50),!
rep(rgb(225,152,105,maxColorValue=255),!
length(rechts)-65))!
farbe_links<-farbe_rechts!
barplot(rechts,axes=F,horiz=T,axis.lty=0,!
border=NA, col=farbe_rechts,xlim=c(-750,750))!
barplot(-links,axes=F,horiz=T,axis.lty=0,border=NA, !
col=farbe_links,xlim=c(-750,750),add=T)!
abline(v=0,lwd=28,col=par("bg"))!
for (i in seq(10,90,by=10)) text(0,i+i*0.2,i,cex=1.1) !
mtext(abs(seq(-600,600,by=200)),!
at=seq(-600,600,by=200), 1,line=-1,cex=0.80)!
rect(-1000,15+15*0.2,1000,66+66*0.2,xpd=T, !
col=rgb(210,210,210,90,maxColorValue=255),!
border=NA)!
mtext("erwerbsfähiges Alter",2,line=1.5,las=3,adj=0.38) !
mtext("Männer",3,line=-5,adj=0.25,cex=1.5,col="grey") !
mtext("Frauen",3,line=-5,adj=0.75,cex=1.5,col="grey") !
mtext("Altersaufb...",3,line=-1.5,adj=0,cex=1.75,!
family="Lato Black",outer=T) !
mtext("Angaben in...",3,line=-3.25,adj=0,cex=1.25,!
font=3,outer=T) !
mtext("Quelle: ww...",1,line=0,adj=1.0,cex=0.95,!
font=3,outer=T)!
Rahlf, T. (2014) Datendesign mit R, S. 222 ff.](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-6-320.jpg)

































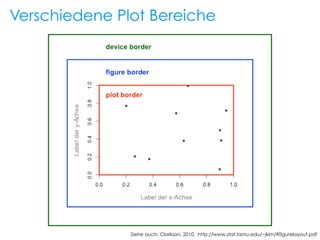
![title.col!
bg!
y.intersep!
box.lwd!
box.col!
legend(1, 10, !
LETTERS[1:3], !
fill=1:4, !
title.col="blue",!
title="Boxen", !
bg="gray90", !
box.col="red", !
box.lwd=3,!
y.intersp=2)!
cex=2!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-43-320.jpg)

















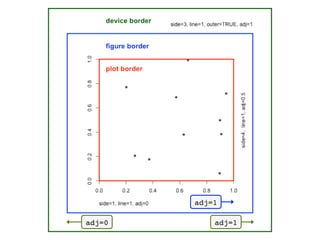
![Verschiedene Plot Bereiche
mar[1] = 5!
oma[1] = 3!
Siehe auch: Clarkson, 2010, chr](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-62-320.jpg)






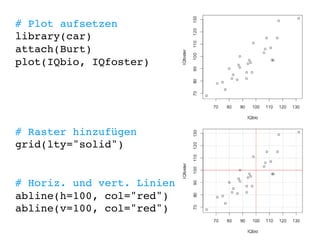
![Definition des Layouts
Die Definition des Layouts geschieht mit Hilfe einer
Matrix
m <- matrix(1:4), ncol=2, by=T)!
m!
[,1] [,2]!
[1,]
1
2!
[2,]
3
4!
Das Erstellen und Aktivieren eines Layouts erfolgt
über die Funktion layout!
layout(m)!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-70-320.jpg)


![Um einen Figure Bereich über mehrere Zeilen
oder Spalten zu erstrecken, bekommen Felder
in der Layout-Matrix dieselbe Zahl zugeteilt.
Felder mit der Zahl 0 bleiben leer und erhalten
keinen Figure Bereich.
m <- matrix(c(1,1,1,!
2,2,0,!
2,2,3), !
ncol=3, !
byrow=T)!
m!
[,1] [,2] [,3]!
[1,]
1
1
1!
[2,]
2
2
0!
[3,]
2
2
3!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-73-320.jpg)







![# Punkte oben rechts in!
# rot neu plotten!
i <- IQbio > 100 & !
IQfoster > 100!
points(IQbio[i], IQfoster[i], !
col = "red", pch = 16)!
# Halb-transparentes !
# Rechteck hinzufügen
rect(100, 100, 140, 140,!
col = "#FF000020",
border = NA)!
!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-82-320.jpg)





![# Leerer plot mit korrekten!
# Limits!
i <- which(IQbio > 130)!
x <- IQbio[i]!
y <- IQfoster[i]!
points(x, y, col = "red", !
pch = 16)!
# Pfeil und Text!
arrows(x, y - 10, !
x, y, !
length=0.2, !
lwd = 2, col = "red")!
text(x, y-12, !
"Sehr schlau", !
adj = 1, col = "red")!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-88-320.jpg)




![Als Zahl
Wenn man eine Zahl eingibt wird die
Standardpalette genutzt
!
palette()!
[1] "black"
[4] "blue"
[7] "yellow"
"red"
"cyan"
"gray" !
"green3" !
"magenta"!
Die Zahl 0 heißt keine Farbe, d.h. weiß,
wenn der Hintergrund der Grafik weiß ist.](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-93-320.jpg)


![Farben als Namen
colors()!
[1] "white"
[4] "antiquewhite1"
[7] "antiquewhite4"
[10] "aquamarine2"
"aliceblue"
"antiquewhite2"
"aquamarine"
"aquamarine3"
"antiquewhite"
"antiquewhite3"
"aquamarine1"
"aquamarine4"
!
!
!
!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-96-320.jpg)

![Grautöne
grey(0)!
[1] "#000000"!
!
grey(.5)!
[1] "#808080"!
!
grey(1)!
[1] "#FFFFFF"!
!
"grey0"!
!
!
"grey50"!
!
!
"grey100"!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-98-320.jpg)
![RGB Modell
CC: By SharkD on http://en.wikipedia.org/wiki/File:AdditiveColor.svg
rgb(1,1,1)!
Funktion rgb setzt Farben aus
Rot-Grün-Blau Anteilen
zusammen
Anteil kann jeweils von 0 bis 1
reichen
Die Funktion gibt einen String
zurück
rgb(.4, .2, .8)!
[1] "#6633CC"!
rgb(0,1,0)! rgb(0,1,1)!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-99-320.jpg)
![RGB Modell
rgb(255,255,255, max=255)!
CC: By SharkD on http://en.wikipedia.org/wiki/File:AdditiveColor.svg
Häufig werden die Anteile
auch mit Werten zwischen 0
und 255 genutzt.
rgb(102, 51, 204, max=255)!
[1] "#6633CC"!
!
rgb(0,255,0,max=255)!](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-100-320.jpg)


![RGB Modell in Hexadezimal-Notation
Hex
Dezimal
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
A
10
B
11
C
12
D
13
E
14
F
15
rgb(0,255,0, max=255)!
[1] "#00FF00"!
Dezimalsystem mit Basis 10
255 = 2 ⋅101 + 5⋅101 + 5⋅10 0
Hexa-Dezimalsystem mit Basis 16
1
255 = 15⋅16 +15⋅16
F
0
F
Merksatz: 0=00 und 255=FF, alles
andere liegt dazwischen](https://image.slidesharecdn.com/basegraphics-140116145910-phpapp02/85/R-base-graphics-103-320.jpg)