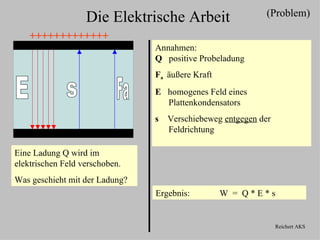
1. (Problem)
Die Elektrische Arbeit
+++++++++++++
Annahmen:
Q positive Probeladung
Fa äußere Kraft
E homogenes Feld eines
Plattenkondensators
s Verschiebeweg entgegen der
Feldrichtung
Eine Ladung Q wird im
elektrischen Feld verschoben.
Was geschieht mit der Ladung?
Ergebnis: W = Q*E*s
Reichert AKS

2. Die Elektrische Arbeit (Herleitung)
+++++++++++++
Ergebnis W=QEs
E ist entgegen s gerichtet
W > 0 für +q
es muss Arbeit gegen das Feld aufgewendet
werden. Die potenzielle Energie der Probeladung
wird erhöht
W < 0 für –q
o
α=0 es wird Arbeit bei der Bewegung der Ladung
gewonnen. Die Probeladung verliert an potenzieller
W = Fa s cos(α) Energie
mit Fa = Q E und cos(0) = 1
W=QEs
Reichert AKS

3. Die Elektrische Arbeit (Beispiel)
++++++++++++ Beispiel: q = 1 nC, E = 1 mV/m, d = 1 mm
Die positive Ladung wird von oben nach
unten bewegt
-, da E und s
gleichgerichtet
Ergebnis: W = - q E d cos(0)
= -10-9 C * 10-3 Nm / C m * 10-3 m
W = -1 * 10-15 J
Die Probeladung verliert an potenzieller Energie
(negatives Vorzeichen)
Reichert AKS

4. Die Elektrische Arbeit (Ausblick)
Ein Elektron bewegt sich auf einer
parabelförmigen Bahn,
sobald es dem Einfluss eines
elektrischen Feldes ausgesetzt ist!
+++++++++++++
Reichert AKS

5. Die Elektrische Arbeit Quellen
J. Grehn; Metzler Physik 12; Metzlersche
Verlagsbuchhandlung Stuttgart 2002; S. 190 ff.1988
Hammer; Physik 12; Oldenbourg Verlag 2002; S. 21
E. Purcell; Elektrizität und Magnetismus; Vieweg
1979; S. 6 ff.
E. Purcell; Elektrizität und Magnetismus; Vieweg
1979; S. 6 und 38 ff.
Reichert AKS