15-mal heruntergeladen
Hochgeladen vonguest58e249
3,996 aufrufe
Winterfeld Jens
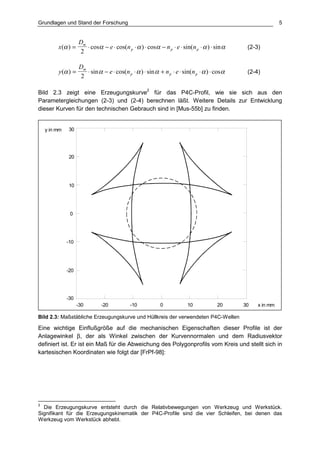
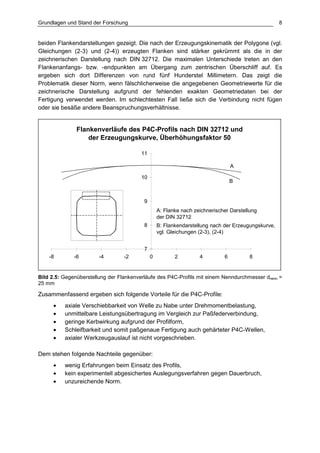
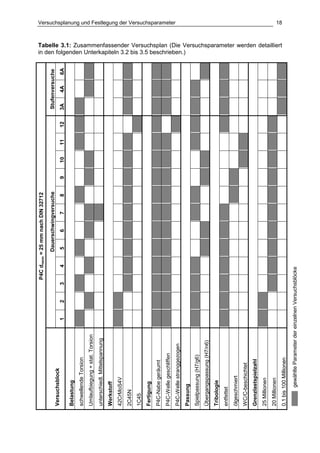
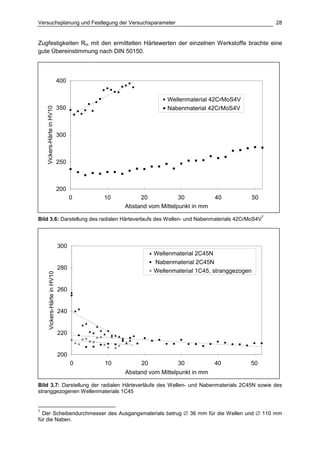
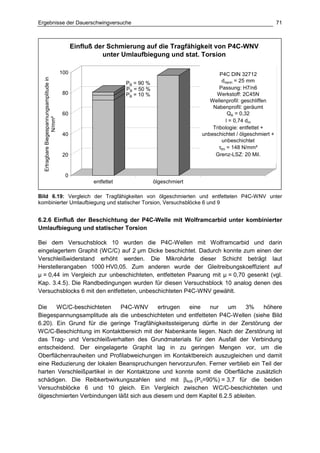
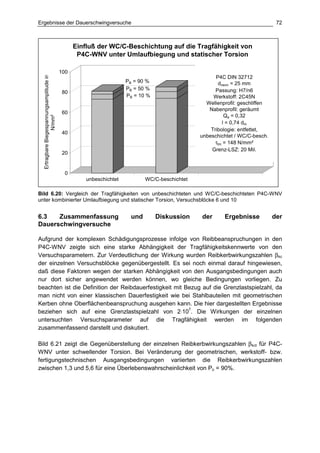
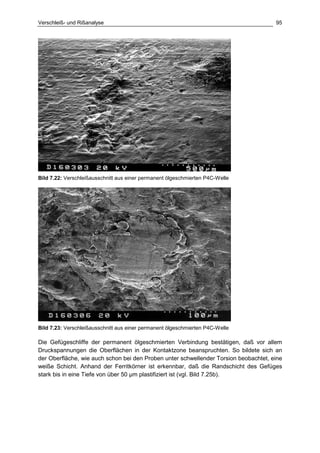
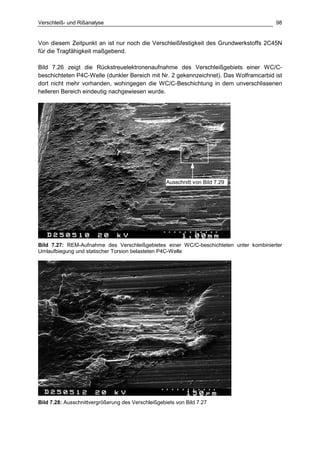
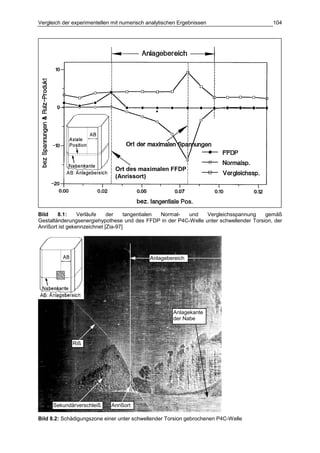
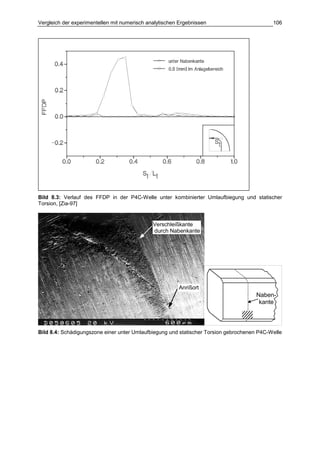
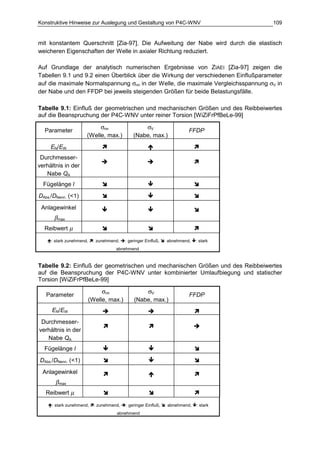
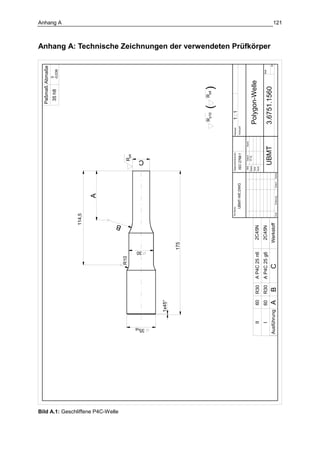
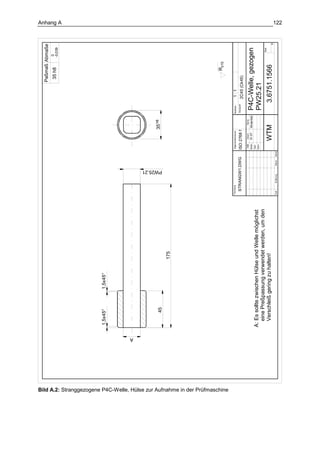
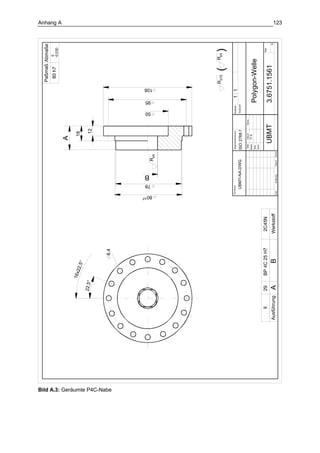
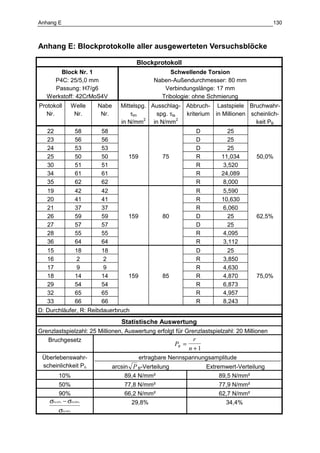
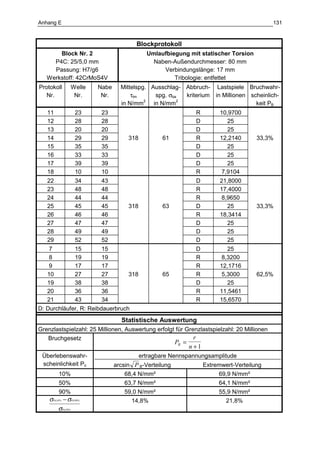
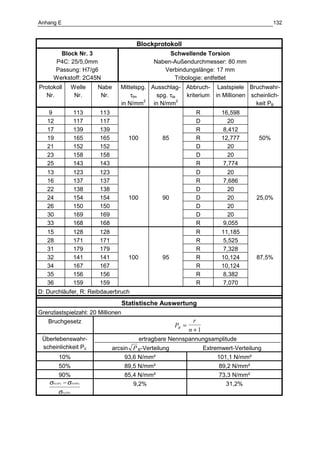
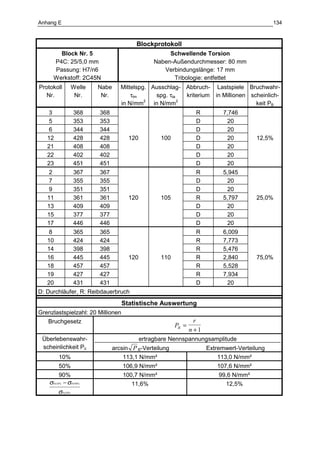
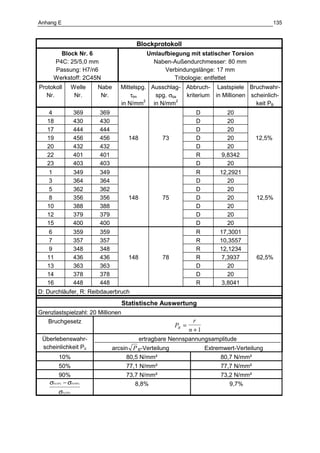
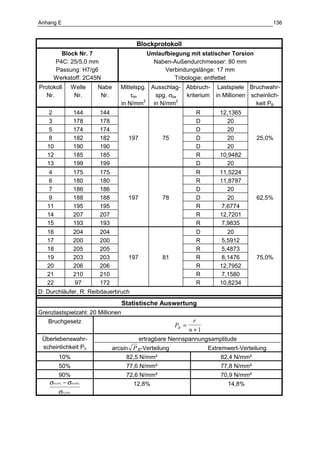
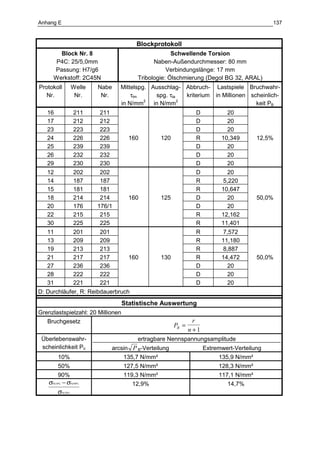
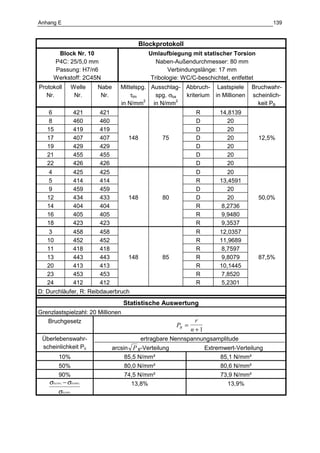
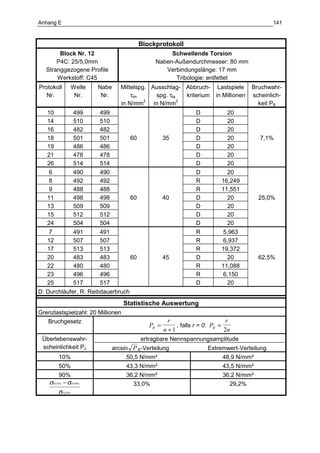
Die Dissertation von Jens Winterfeld untersucht die Einflüsse der Reibdauerbeanspruchung auf die Tragfähigkeit von P4C-Welle-Nabe-Verbindungen. Es werden sowohl analytische als auch experimentelle Methoden genutzt, um die Auswirkungen von verschiedenen Materialien und geometrischen Parametern unter unterschiedlichen Belastungsbedingungen zu analysieren. Abschließend bietet die Arbeit konstruktive Hinweise zur Auslegung und Gestaltung dieser Verbindungen sowie einen Ausblick auf zukünftige Forschung.
