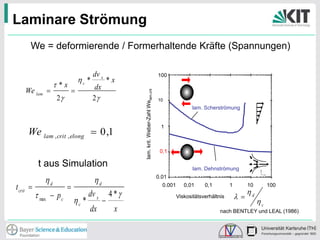
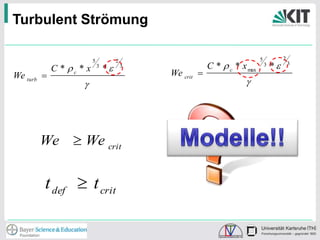
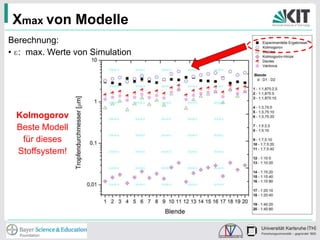
Die Studie untersucht den Tropfenaufbruch in Hochdruckdüsen durch experimentelle und simulierte Analysen. Dabei werden verschiedene Lochblenden getestet, um optimale Bedingungen für die Homogenisierung zu bestimmen, wobei die Dehnrate und Turbulenz entscheidend für die Tropfenzerkleinerung sind. Die Ergebnisse zeigen, dass ein optimales Verhältnis von Düsen und Strömungsverhältnissen die Effizienz des Prozesses verbessert.

1. Experimentelle Untersuchungen und
Simulation von Hochdruckdüsen
Marília Rauck
Betreuer:
Dipl.- Wi.- Ing. Karsten Köhler
Prof. Dr.- Ing. H.P. Schuchmann
11.09.2009

2. Brasilien

3. Gliederung
• Motivation
• Grundlagen des Tropfenaufbruchs
• Untersuchungen von Standard-Lochblenden
• Untersuchungen von SHM-Blenden

4. Kraft
Besseres Verständnis des
Tropfenaufbruch
Dehnung
Kavitation
Zeit t [ms]
Turbulenz

5. Grundlegender Ablauf der Homogenisierung
• Wann findet der Tropfenaufbruch statt?
1. Wenn angreifende Spannungen größer sind als Formerhaltende
Kräften.
We > Wecrit
1. Wenn die Spannungen lang genug anhalten.
t > tcrit
• Wie bricht der Tropfen auf?
5 | Marilia Rauck | BLT: Lebensmittelverfahrenstechnik |

6. Laminare Strömung
We = deformierende / Formerhaltende Kräfte (Spannungen)
 *x
2

dv x
100
*x
dx
2
We lam , crit , elong  0 ,1
lam. krit. Weber-Zahl Welam,crit
We lam 
c *
10
lam. Scherströmung
1
0,1
t aus Simulation
t crit 
d
 max
d

dv x 4 * 
 pc
c *

dx
x
lam. Dehnströmung
0.01
0.001
0,01
0,1
1
Viskositätsverhältnis
10

d
100
c
nach BENTLEY und LEAL (1986)

7. Relaxation
t crit 
400
3,5E+05
350
z
3,0E+05
Dehnrate e / s-1
300
2,5E+05
Einphasige Simulation
c = 1 mPa·s
z = 0 mm: Einlauf in
den Blendeneingang
d = 0,4 mm
Dp = 50 bar
d = 0,4 mm
2,0E+05
1,5E+05
1,0E+05
5,0E+04
0,0E+00
Dehnrate
-5,0E+04
250
200
150
100
50
turb. kinetische. Energie
-1,0E+05
0
-2
0
2
4
Abstand z / mm
t res
6
8
10
Spez. turbulente kinetische Energie k / m2·s2
4,0E+05
d
 max
d

 pc 4 * 
x
Relaxation findet
statt wenn
t res  t crit

8. Turbulent Strömung
We turb 
C * c * x
5
3
*e
2
3

We  We crit
t def  t crit
We crit 
C *  c * x max

5
3
*e
2
3

9. Modelle für ε
• Kolmogorov
• Isuru N. et. al.
e K  C k ou '
eI 
3
P * V or
2 ,5 * d or *  e

10. Modelle für Xmax
• Kolmogorov
Oh 
x max, ( Oh  )  e
d
 *  d * x 
1
2
x max, ( Oh  )  e
2
5
1
*
*
4
3
3
* c
5
5
3
3
4
* c
4
• Walstra
l 0  Pv
1
3
4
x max (  l 0 )  
1
* c 4 *  c
2
3
5
* Pv
1
5
* c
5
2
x Max (  l 0 )   * Pv
1
1
2
* c
2

11. Modelle für Xmax
x max  A1 (   A 2 d e
1
Viscosity range
KolmogorovHinze, 1955
Sprow,
1967
Davies, 1985
Calabrese et
al.,
1986
Vankova, N.
et. al.,
2007
1
3
3
3
3
x max )
Interfacial
tension
5
 c 5e
A1
2
5
A2
Coaxial cylinders
low
0.725
Impellers
0.51 mPa.s
41.8 mN/m
0.138
Clearance valve
Colloidal mills
Liquid whistles
Turbine impellers
3.5 to 200 mPa.s
 30 mN/m
1
( 0.354)
Impellers
5 to 500 mPa.s
1 to 45 mN/m
 0.09
4.08 – 4.42
Narrow-gap
homogenizer
3 to 500 mPa.s
5 to 30 mN/m
0.944
0.28

12. Gliederung
• Motivation
• Grundlagen des Tropfenaufbruchs
• Untersuchungen von Standard-Lochblenden
• Untersuchungen von SHM-Blenden

13. Material und Methoden
Rohemulsion
0,25% Pflanzenöl
5% SDS Emulgator
demineralisiertes Wasser
Microfluidizers
100 bar
BECKMAN COULTER
LS 13.320
Tropfengroßverteilungen der Emulsion
X90,3%

14. Material und Methoden
CFD Strömungssimulationssoftware FLUENT® 6.2
1-phasig (Wasser)
RNG k-ɛ-Modell
Simulation
Auswertung
Geschwindigkeit
Druck
Dehnraten
turbulente kinetischen Energie k
turbulente Dissipation ɛ

15. Material und Methoden
L
(mm)
D1
(mm)
d
(mm)
D2
(mm)
0,4
1,5
4
0,1
0,2
0,4
0,8
2
4
8
Verhältnis:
1 : D1/d : D2/d

16. Ermittlung der Dehnung
N
Dehnung

 (  90 % Dehngung
i
N
max
)

17. Ermittlung der Turbulent Dissipation Rate
N
e 
 (  90 % e
i
N
max
)

18. Dehnung steigt mit steigendem D1/d-Verhältnis
Mit steigendem D2/d-Verhältnis sinkt die Dehnung

19. Je größer die max. Dehnung, desto
größer die Tropfen

20. Turbulenz steigt
- mit steigendem D2/d-Verhältnis
- mit sinkendem D1/d-Verhälntis

21. Je Größer die Turbulenz desto Größer die
Tropfen

22. Experimentelle Ergebnisse
X90,3%
Verhältnis
1mm:1,875mm:10mm

23. Xmax von Modelle
Berechnung:
• ɛ: max. Werte von Simulation
Kolmogorov
Beste Modell
für dieses
Stoffsystem!

24. d : D1 : D2 = 1 : 15 : 80
Max.
DehnungAxis
Turbulenz
Bis ≈ 5,6 µm
aufgebrochen
Größeren Tropfen werden
zerkleinert
Neue
Verteilung

25. Zusammenfassung
• Experimentelle Ergebnis
• Optimal Verhältnis: 1: 1,875 : 10
• Simulation
• ↑D2/d → ↓ max. Dehnung und max. ɛ
• ↑max. Dehnung und ↑ max. ɛ → ↑x 90,3%
• max. Dehnung und max. ɛ auf die Axis sind nicht geeignet um die
Tropfenaufbruch zu modellieren
• Modelle
• max. ɛ von Simulation + X max. von Kolmogorov ≈ X 90,3%

26. Gliederung
• Grundlagen des Tropfenaufbruchs
• Untersuchungen von Standard-Lochblenden
• Untersuchungen von SHM-Blenden

27. Material und Methoden
Rohemulsion
0,5% Pflanzenöl
5% SDS Emulgator
demineralisiertes Wasser
Microfluidizers
100 bar
Hauptstrom = Nebenstrom
BECKMAN COULTER
LS 13.320
Tropfengroßverteilungen der Emulsion
X90,3%

28. Material und Methoden
0,8mm
D2
(mm)
0,4mm
D2
0,2mm
2mm
2
4
8
Volumenstromv H
erhältnis
N
E (%)
1:1
0
1
0,5
1:1
0,5
0,5
0,5
1:1
1
0
0,5

29. X90,3% x Disperser Phasenanteil im Hauptstrom
Alles durch
Hauptstrom
vorteilhaft
Auslaufdurchmesser
hat keinen klaren
Einfluss

30. Volumenverteil x Tropfendurchmesser
Disp. Phasenanteil
im Hauptstrom:
0→ Bimodal
0,5 → Monomodal
1 → Monomodal

31. Zusammenfassung
Über Hauptstrom ist vorteilhaft, weil
- Dehnung zusätzlich hilft
- Turbulenz besser genutzt wird.
31 | Marilia Rauck | BLT: Lebensmittelverfahrenstechnik |

33. 33 | Marilia Rauck | BLT: Lebensmittelverfahrenstechnik |