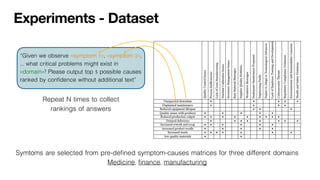
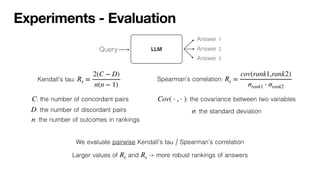
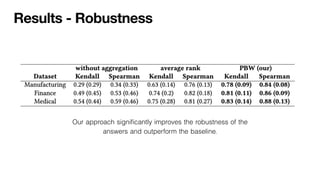
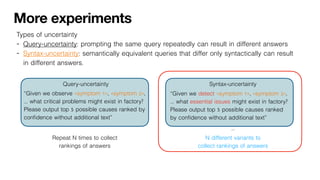
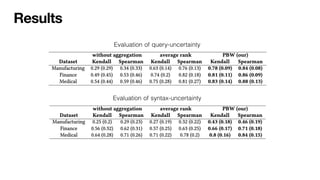
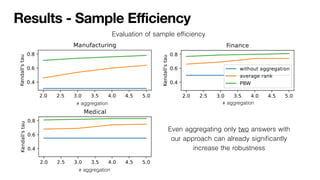
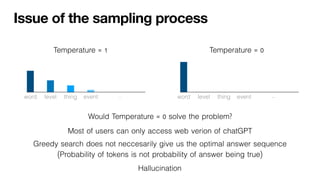
Large-language models (LLMs) can support a wide range of applications like conversational agents, creative writing or general query answering. However, they are ill-suited for query answering in high-stake domains like medicine because they are typically not robust - even the same query can result in different answers when prompted multiple times. In order to improve the robustness of LLM queries, we propose using ranking queries repeatedly and to aggregate the queries using methods from social choice theory. We study ranking queries in diagnostic settings like medical and fault diagnosis and discuss how the Partial Borda Choice function from the literature can be applied to merge multiple query results. We discuss some additional interesting properties in our setting and evaluate the robustness of our approach empirically.

1. Robust Knowledge Extraction
from Large Language Models
using Social Choice Theory
Nico Potyka1, Yuqicheng Zhu2,3, Yunjie He2,3, Evgeny Kharlamov2,4, Steffen Staab3,5
1Cardiff University, UK 2Bosch Center for Artificial Intelligence, Germany
3University of Stuttgart, Germany 4University of Oslo, Norway 5University of Southampton, UK
AAMAS’24, Auckland, New Zealand
This work was partially supported by the Horizon Europe project EnrichMyData (Grant Agreement No.101070284)

2. Overview

3. Large Language Models (LLMs)
The goal of LLMs is to predict the next ???
Transformer
Sampling Token
word level thing event …
Probability distribution of the next token
P(Tn+1 |T1, …, Tn)

4. Issue of the sampling process
Query:
“A 20 year old professional runner suffers from a stinging pain in the forefoot. The foot
is swollen and stiff. What are the top 3 plausible explanations? Please keep the answer
short and order by decreasing plausibility.”
0.15 Overuse Injury
0.08 Tendonitis
0.07 Ligament Sprain
…
P(Tnext |Query) P(Tnext |{Query, overuse_injury})
0.20 Tendonitis
0.08 Ligament Sprain
0.05 Infection
…
1. Overuse Injury
2. Tendonitis
3. Ligament Sprain
…
0.15 Overuse Injury
0.08 Tendonitis
0.07 Ligament Sprain
…
P(Tnext |Query) P(Tnext |{Query, Tendonitis})
0.17 Overuse Injury
0.10 Ligament Sprain
0.05 Footwear Issue
…
1. Tendonitis
2. Overuse Injury
3. Footwear Issue
…

5. Would Temperature = 0 solve the problem?
Issue of the sampling process
word level thing event …
Temperature = 1
word level thing event …
Temperature = 0
Most of users can only access web verion of chatGPT
Greedy search does not neccesarily give us the optimal answer sequence
(Probability of tokens is not probability of answer being true)
Hallucination

6. Our Expectation
Query:
“A 20 year old professional runner suffers from a stinging pain in the forefoot. The foot
is swollen and stiff. What are the most plausible explanations? Please keep the answer
short and order by decreasing plausibility.”
1. Overuse Injury
2. Tendonitis
3. Ligament Sprain
1. Footwear Issues
2. Overuse Injury
3. Infection or Insert Bite
1. Overuse Injury
2. Footwear Issues
3. Tendonitis
1. Overuse Injury
2. Footwear Issues
3. Tendonitis
4. Ligament Sprain
5. Infection or Insert Bite
Ranking Aggregation?
0.35
0.30
0.15
0.10
0.10
Robust ranking -> <- Uncertainty quantification

7. Scoring-based Voting
A
B
C
≻1 ≻2 ≻3 ≻
1. A
2. B
3. C
≻1
1. B
2. A
3. C
≻2
1. A
2. C
3. B
≻3
Borda Voting
w≻(o) = |{o′ ∈ O|o ≻ o′}|
McLean, Iain; Urken, Arnold B.; Hewitt, Fiona (1995). Classics of Social Choice. University of Michigan Press. ISBN 978-0-472-10450-5.

8. Scoring-based Voting
A 2
B 1
C 0
≻1 ≻2 ≻3 ≻
1. A
2. B
3. C
≻1
1. B
2. A
3. C
≻2
1. A
2. C
3. B
≻3
Borda Voting
w≻(o) = |{o′ ∈ O|o ≻ o′}|
McLean, Iain; Urken, Arnold B.; Hewitt, Fiona (1995). Classics of Social Choice. University of Michigan Press. ISBN 978-0-472-10450-5.

9. Scoring-based Voting
A 2 1 2 5
B 1 2 0 3
C 0 0 1 1
≻1 ≻2 ≻3 ≻
1. A
2. B
3. C
≻1
1. B
2. A
3. C
≻2
1. A
2. C
3. B
≻3
Borda Voting
w≻(o) = |{o′ ∈ O|o ≻ o′}|
1. A
2. B
3. C
≻
McLean, Iain; Urken, Arnold B.; Hewitt, Fiona (1995). Classics of Social Choice. University of Michigan Press. ISBN 978-0-472-10450-5.

10. Partial Borda Weighting (PBW)
[1] Cullinan, J., Hsiao, S. K., & Polett, D. (2014). A Borda count for partially ordered ballots. Social Choice and Welfare, 42(4), 913-926. http://www.jstor.org/stable/43662509
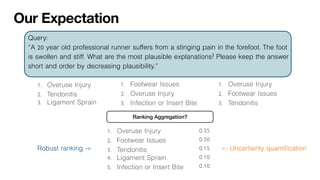
1. Overuse Injury
2. Tendonitis
3. Ligament Sprain
≻1
1. Footwear Issues
2. Overuse Injury
3. Infection or Insert Bite
≻2
1. Overuse Injury
2. Footwear Issues
3. Tendonitis
≻3
Partial Ordering Partial Borda Weighting [1]
w≻(o) = 2 ⋅ Down≻(o) + Inc≻(o)
Down≻(o) = |{o′ ∈ O|o ≻ o′}|
Inc≻(o) = |{o′ ∈ O|o and o′ are incomparable|
Overuse Injury (OI) 8
Tendonitis (TD) 6
Ligament Sprain (LS) 4
Footwear Issues (FI) 1
Infection or Insert Bite (II) 1
≻1 ≻2 ≻3 ≻
w≻1
(OI) = 2 ⋅ 4 + 0 = 8
w≻1
(TD) = 2 ⋅ 3 + 0 = 6
w≻1
(LS) = 2 ⋅ 2 + 0 = 4
w≻1
(FI) = 0 + 1 = 1
w≻1
(II) = 0 + 1 = 1

11. Partial Borda Weighting (PBW)
[1] Cullinan, J., Hsiao, S. K., & Polett, D. (2014). A Borda count for partially ordered ballots. Social Choice and Welfare, 42(4), 913-926. http://www.jstor.org/stable/43662509
Overuse Injury (OI) 8 6 8 20
Tendonitis (TD) 6 1 4 11
Ligament Sprain (LS) 4 1 1 6
Footwear Issues (FI) 1 8 6 15
Infection or Insert Bite (II) 1 4 1 6
≻1 ≻2 ≻3 ≻
1. Overuse Injury
2. Tendonitis
3. Ligament Sprain
≻1
1. Footwear Issues
2. Overuse Injury
3. Infection or Insert Bite
≻2
1. Overuse Injury
2. Footwear Issues
3. Tendonitis
≻3
Partial Ordering Partial Borda Weighting [1]
w≻(o) = 2 ⋅ Down≻(o) + Inc≻(o)
Down≻(o) = |{o′ ∈ O|o ≻ o′}|
Inc≻(o) = |{o′ ∈ O|o and o′ are incomparable|
1. OI
2. FI
3. TD
4. LS
4. II
≻
0.35
0.26
0.19
0.10
0.10

12. Partial Borda Weighting (PBW)
Theorem (Cullinan et al. 2014): The PBW social choice function is the unique function that satisfies:
- Consistency: the choice for two independent sets of rankings is consistent with the choice for their union,
- Faithfulness: an alternative that is dominated by another on cannot be chosen,
- Neutrality: the choice of alternatives is independent of their identity,
- Cancellation: if no alternative dominates another one, the function will be indifferent between the alternatives.
[1] Cullinan, J., Hsiao, S. K., & Polett, D. (2014). A Borda count for partially ordered ballots. Social Choice and Welfare, 42(4), 913-926. http://www.jstor.org/stable/43662509
Proposition: The PBW score give us the following additional guarantees:
- Partial Agreement: if alternative dominates , then
- Full Agreement: if all rankings agree, then the scores will be consistent with the ranking
- Domination: if alternative dominates all alternative, then receives the maximum score
a1 a2 score(a1) > score(a2)
a* a*

13. Experiments - Dataset
Symtoms are selected from pre-defined symptom-causes matrices for three different domains
Medicine, finance, manufacturing
“Given we observe <symptom 1>, <symptom 2>,
… what critical problems might exist in
<domain>? Please output top 5 possible causes
ranked by confidence without additional text”
Repeat N times to collect
rankings of answers

14. Experiments - Evaluation
Kendall’s tau: Rτ =
2(C − D)
n(n − 1)
: the number of concordant pairs
C
: the number of discordant pairs
D
: the number of outcomes in rankings
n
Spearman’s correlation: Rs =
cov(rank1,rank2)
σrank1 ⋅ σrank2
: the covariance between two variables
Cov( ⋅ , ⋅ )
: the standard deviation
σ
We evaluate pairwise Kendall’s tau / Spearman’s correlation
Larger values of and -> more robust rankings of answers
Rτ Rs
LLM
Query
Answer 1
Answer 2
Answer 3

15. Results - Robustness
Our approach significantly improves the robustness of the
answers and outperform the baseline.

16. More experiments
Types of uncertainty
- Query-uncertainty: prompting the same query repeatedly can result in different answers
- Syntax-uncertainty: semantically equivalent queries that differ only syntactically can result
in different answers.
“Given we observe <symptom 1>, <symptom 2>,
… what critical problems might exist in factory?
Please output top 5 possible causes ranked by
confidence without additional text”
Query-uncertainty
Repeat N times to collect
rankings of answers
Syntax-uncertainty
“Given we detect <symptom 1>, <symptom 2>,
… what essential issues might exist in factory?
Please output top 5 possible causes ranked
by confidence without additional text”
…
N different variants to
collect rankings of answers

17. Results
Evaluation of query-uncertainty
Evaluation of syntax-uncertainty

18. Results - Sample Efficiency
Evaluation of sample efficiency
# aggregation # aggregation
# aggregation
Even aggregating only two answers with
our approach can already significantly
increase the robustness

19. Summary and outlook
• To improve the robustness of the answer from LLMs, we suggest
to sample answers repeatly and to aggregate the answers using
social choice theory.
• Our approach (PBW) gives several interesting analytical
guarantees and significantly improve robustness against both
query- and syntax uncertainty.
• Can our approach improve robustness against adversarial
attacks in queries?
Poster: 76A – 78B

20. Thanks