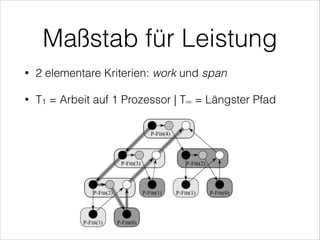
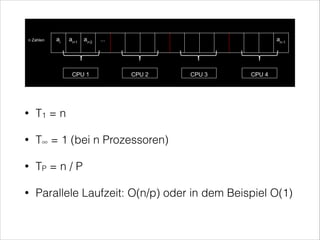
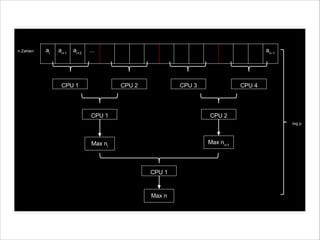
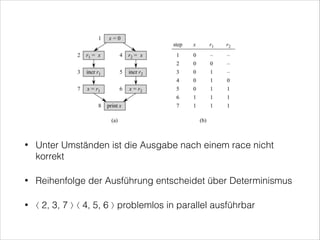
Das Dokument behandelt multithreaded Algorithmen, insbesondere den parallelen Mergesort, und erläutert technische Aspekte sowie die Leistungsanalyse von Algorithmen im Kontext mehrerer Prozessoren. Es wird beschrieben, wie parallele Berechnungen durchgeführt werden können, während Herausforderungen wie Race Conditions und die Notwendigkeit der Synchronisation angesprochen werden. Zudem wird die Effizienz des parallelen Mergesorts im Vergleich zu herkömmlichem Mergesort hervorgehoben, wobei bedeutende Leistungsgewinne erzielt werden können.

1. Multithreaded Algorithms
Cormen, Thomas H., Introduction to Algorithms
Third Edition
Universität zu Köln
Institut für Informatik
Prof. Dr. Michael Jünger
!
Referent: Kersten Broich
24. Januar 2014

2. Übersicht
•
Einleitung
•
•
Beispiele
•
Messbarkeit / Qualität
•
•
Technische Hintergründe
Schwierigkeiten
Multithreaded MergeSort()
•
Klassisches MergeSort() / Naive parallele Erweiterung
•
Idee hinter parallelem MergeSort()
•
Umsetzung und Analyse aller Teilaufrufe

3. Rückblick Informatik I
•
Ausschließlich serielle Algorithmen
•
RAM-Model (Random Access Machine)
•
Eine CPU führt Rechenoperationen aus

4. Mehrkern-Systeme
•
Mittlerweile überall vertreten
•
Idee dahinter ist bereits einige Jahrzehnte alt
•
Multitasking/Multiprocessing
•
Kernpunkt: Ausführung von Operationen parallel
auf mehreren Recheneinheiten bei gesteigerter
Geschwindigkeit

5. Dynamic Multithreaded
Programming
•
concurrency platform

6. Restriktionen
•
Nicht alle Probleme lassen sich übergangslos
parallel berechnen
•
Aufrufe müssen unabhängig voneinander ablaufen,
ohne das ihre Reihenfolge einen Einfluss auf das
Ergebnis hat
•
Divide & Conquer

7. Maßstab für Leistung
•
2 elementare Kriterien: work und span
•
T1 = Arbeit auf 1 Prozessor | T∞ = Längster Pfad

8. Beispiel 1
•
Laufe durch das Array A und quadriere A[i]
•
Serielle Laufzeit: O(n)

9. •
T1 = n
•
T∞ = 1 (bei n Prozessoren)
•
TP = n / P
•
Parallele Laufzeit: O(n/p) oder in dem Beispiel O(1)

10. Beispiel 2
•
findMax(int[] A)
•
Serielle Laufzeit: O(n)

12. Beispiel 2 Analyse
•
Laufzeit: n / P + log P
•
Parallele Ausführung muss synchronisiert werden
•
Beispiel: log P wird durch erneutes Delegieren der
findMax() Methode addiert

13. Speedup
•
Wie schnell ist die Berechnung auf P Prozessoren
im Vergleich zu Systemen mit 1 Prozessor
•
Speedup = T1 / TP
•
Perfect Linear Speedup, wenn T1 / TP = P
(wird in der Praxis nie erreicht)

14. Parallelität
•
Verhältnis T1 / T∞
•
Wie viel Arbeit kann durchschnittlich in einem
Schritt parallel verrichtet werden?
•
Je mehr Prozessoren im Verhältnis zur Parallelität,
desto schlechter ist der Speedup
P ≫ T1 / T∞
T1/TP ≪ P

15. Race Conditions
•
Deterministischer Algorithmus, wenn eindeutig
definierte, reproduzierte Zustände auftreten
•
Determinacy Race
•
entsteht, wenn 2 parallele Anweisungen den
identischen Speicherplatz eines Datums
ansprechen und mindestens eine der beiden eine
WRITE-Operation durchführt.

16. •
Lese x aus dem Speicher in das Register des
Prozessors
•
Erhöhe den Wert von x um 1
•
Schreibe den Wert aus dem Register zurück in den
Speicher

17. •
Unter Umständen ist die Ausgabe nach einem race nicht
korrekt
•
Reihenfolge der Ausführung entscheidet über Determinismus
•
⟨ 2, 3, 7 ⟩ ⟨ 4, 5, 6 ⟩ problemlos in parallel ausführbar

18. Multithreaded
Merge Sort

19. MergeSort (klassisch)

20. MergeSort’ (naiv)
•
Paralleler Ansatz: Aufspannen des ersten rekursiven Aufrufs
und parallele Bearbeitung von MergeSort’(A, p, q) und
MergeSort’(A, q+1, r)

21. Analyse MergeSort’(A, p, r)
•
Da Merge'() seriell durchgeführt wird, sind sowohl work als
auch span Θ(n)
•
work:
MS’1 = 2MS’1(n/2) + Θ(n)
= Θ(n log n)
span:
•
MS’∞ = MS’∞(n/2) + Θ(n)
= Θ(n)

22. •
Das ist identisch mit der seriellen Laufzeit in der
klassischen MergeSort() Variante O(n log n)
•
Die Parallelität des naiven Ansatz:
MS’1(n)/MS’∞(n) = Θ(log n)
•
Der Flaschenhals-Effekt entsteht beim seriellen
Merge() Verfahren
•
Auch wenn das Vereinigen der beiden Teilfolgen
vordergründig ausschliesslich serielles Vorgehen
zuzulassen scheint, kann eine parallele Methode
verwendet werden

23. Idee

24. •
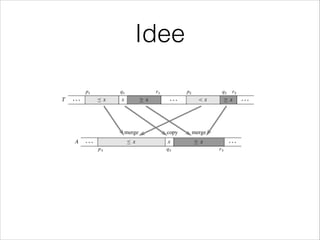
Array T[] und Array A[]
•
Zwei (sortierte) Teilfolgen
T[p1..r1] mit n1 = r1 - p1 + 1
T[p2..r2] mit n2 = r2 - p2 + 1
•
werden vereinigt in
A[p3..r3] der Länge n3 = r3 - p3 + 1 = n1 + n2

25. •
Wir nehmen an n1 ≥ n2
•
•
Identifizieren von x = T[q1] der sortierten Teilfolge
T[p1..r1] an der Stelle
q1 = (p1 + r1) / 2
x ist somit der Median von T[p1..r1]

26. •
Jedes Element in T[p1..q1 - 1] ≤ x
•
Jedes Element in T[q1 + 1..r1] ≥ x
•
Mit Hilfe von BinarySearch() wird anschliessend
das Element T[q2] ermittelt, um sicherzustellen,
dass T[p2..r2] nach dem Einfügen von x zwischen
T[q2-1] und T[q2] immer noch sortiert ist

27. Anschließend Vereinigen der Teilfolgen T[p1..r1] und T[p2..r2] nach
A[p3..r3] in folgenden Schritten:
•
1. Setze q3 = p3 + (q1 - p1) + (q2 - p2)
2. Kopiere x nach A[q3]
3. Rekursives Merge() von T[p1..q1 - 1] mit T[p2..q2 - 1] und setze
das Ergebnis in die Teilfolge A[p3..q3 - 1]
4. Rekursives Merge() von T[q1 + 1..r1] mit T[q2..r2] und setze das
Ergebnis in die Teilfolge A[q3 + 1..r3]

28. BinarySearch()

29. Binary Search
•
Die Prozedur BinarySearch(x, T, p, r) erhält einen Schlüssel x und
eine Teilfolge T[p..r] und gibt eine der folgenden Werte zurück:
•
•
Wenn x ≤ T[p] und daher ≤ alle Elemente in T[p..r]:
Rückgabewert: Index p
•
•
Wenn T[p..r] leer ist (r < p)
Rückgabewert: Index p
Wenn x > T[p] dann gebe den größten Index q in dem Bereich p
< q ≤ r + 1, so dass gilt T[q-1] < x zurück
Aufgrund der seriellen Bearbeitung wird daher Θ(log n) im
schlechtesten Fall benötigt. Work und span können also insgesamt
mit Θ(log n) abgeschätzt werden

30. ParallelMerge()

31. Analyse von
ParallelMerge()
•
Zuerst wird span betrachtet:
ParallelMerge() wird rekursiv aufgerufen und findet
parallel statt. Daher muss nur der aufwendigere der
beiden Aufrufe analysiert werden
•
Die maximale Anzahl an Elementen in einer der
beiden rekursiven Aufrufe ist max. 3n / 4

32. Im schlechtesten Fall führt ein rekursiver Aufruf n1/2
Elemente aus T[p1..r1] mit allen n2 Elementen aus T[p2..r2]
zusammen:
•
n1/2+ n2 ≤ n1/2 + n2/2 + n2/2
= (n1 + n2) / 2 + n2/2
≤ n/2 + n/4
= 3n / 4
Gemeinsam mit O(log n) aus BINARY-SEARCH ergibt sich
eine Gesamtabschätzung von:
•
PM∞(n) = PM∞(3n/4) + Θ(log n)
PM∞(n) = Θ(log2 n)

33. •
Analyse von work PM1(n) von ParallelMerge() mit n
Elementen: Θ(n), da jedes Element von Array T in
Array A kopiert werden muss.
•
im schlechtesten Fall kostet der BinarySearch()
Aufruf zusätzlich Θ(log n).
•
Die Parallelität von ParallelMerge() ist demnach
PM1(n)/PM∞(n) = Θ(n / log2 n)

34. ParallelMergeSort()

35. ParallelMergeSort()
(Analyse)
Analyse von work bei ParallelMergeSort()
•
PMS1(n) = 2 PMS1(n/2) + PM1(n)
= 2 PMS1(n/2) + Θ(n)
•
Identisch mit klassischem MergeSort() mit
PMS1(n) = Θ(n log n)

36. worst case span für PMS∞(n): Da sich
ParallelMergeSort() zweimal rekursiv aufruft, kann
eine der beiden ignoriert werden:
•
PMS∞(n) = PMS∞(n/2) + PM∞(n)
= PMS∞(n/2) + Θ(log2 n)
•
span ist PMS∞(n) = Θ(log3 n)

37. ParallelMergeSort() bringt signifikante Vorteile in der
Parallelität gegenüber dem naiven MergeSort()’, dass das
serielle Merge()-Verfahren verwendet:
•
Parallelität MergeSort()’ (naiv)
PM’1(n) / PMS∞(n) = Θ(n log n) / Θ(n)
= Θ(log n)
Parallelität ParallelMergeSort()
PMS1(n) / PMS∞(n) = Θ(n log n) / Θ(log3 n)
= Θ(n / log2 n)
•
deutlich besser in Theorie und Praxis

38. Vielen Dank für Ihre
Aufmerksamkeit!