FunçõEs, Quais As Suas FunçõEs
•Als PPT, PDF herunterladen•
0 gefällt mir•395 views
Melden
Teilen
Melden
Teilen
Weitere ähnliche Inhalte
Was ist angesagt?
Was ist angesagt? (14)
Introdução a função exercícios - Professor Walter Brotto

Introdução a função exercícios - Professor Walter Brotto
Andere mochten auch
Andere mochten auch (8)
Ähnlich wie FunçõEs, Quais As Suas FunçõEs
Ähnlich wie FunçõEs, Quais As Suas FunçõEs (20)
Produto cartesiano e função 1º ano do ensino medio

Produto cartesiano e função 1º ano do ensino medio
Produto cartesiano e função 1º ano do ensino medio

Produto cartesiano e função 1º ano do ensino medio
004 - RELAÇÃO ENTRE FUNÇÕES - FUNÇÕES INVERSA - BIJETORA - INJETORA E COMPOST...

004 - RELAÇÃO ENTRE FUNÇÕES - FUNÇÕES INVERSA - BIJETORA - INJETORA E COMPOST...
Mehr von pollysoares
Mehr von pollysoares (7)
Kürzlich hochgeladen
Aula de tema de redação desenvolvida pela professora Ana Augusta Lages, graduanda em Letras pela UFMGTema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...AnaAugustaLagesZuqui
Kürzlich hochgeladen (20)
O estudo do controle motor nada mais é do que o estudo da natureza do movimen...

O estudo do controle motor nada mais é do que o estudo da natureza do movimen...
Novena de Pentecostes com textos de São João Eudes

Novena de Pentecostes com textos de São João Eudes
atividade-de-portugues-paronimos-e-homonimos-4º-e-5º-ano-respostas.pdf

atividade-de-portugues-paronimos-e-homonimos-4º-e-5º-ano-respostas.pdf
República Velha (República da Espada e Oligárquica)-Sala de Aula.pdf

República Velha (República da Espada e Oligárquica)-Sala de Aula.pdf
Apresentação | Símbolos e Valores da União Europeia

Apresentação | Símbolos e Valores da União Europeia
Educação Financeira - Cartão de crédito665933.pptx

Educação Financeira - Cartão de crédito665933.pptx
Slides Lição 06, Central Gospel, O Anticristo, 1Tr24.pptx

Slides Lição 06, Central Gospel, O Anticristo, 1Tr24.pptx
Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...

Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...
ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024

ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024
Considerando as pesquisas de Gallahue, Ozmun e Goodway (2013) os bebês até an...

Considerando as pesquisas de Gallahue, Ozmun e Goodway (2013) os bebês até an...
Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...
E a chuva ... (Livro pedagógico para ser usado na educação infantil e trabal...

E a chuva ... (Livro pedagógico para ser usado na educação infantil e trabal...
MESTRES DA CULTURA DE ASSARÉ Prof. Francisco Leite.pdf

MESTRES DA CULTURA DE ASSARÉ Prof. Francisco Leite.pdf
O desenvolvimento é um conceito mais amplo, pode ter um contexto biológico ou...

O desenvolvimento é um conceito mais amplo, pode ter um contexto biológico ou...
FunçõEs, Quais As Suas FunçõEs
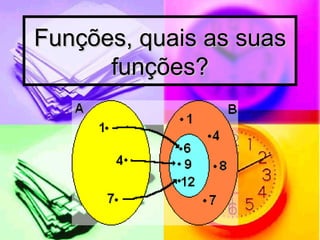
- 1. Funções, quais as suas funções?
- 3. Também variações na pressão sanguínea, onde se relaciona a pressão máxima, com a mínima.
- 5. Relação Binária A relação Binária, é qualquer subconjunto do produto cartesiano A x B A relação R1 de A = {0, 1, 2, 3} em B = {a, b, c, d} dada por R1 = {(0; a), (1; b), (2; c), (2; d)} pode ser representada dos seguintes modos:
- 6. Funções F:A B ou y=f(x), dado que x Adotando dois conjuntos, A e B, não-vazios e uma relação binária de A em B, dizemos que essa relação é função de A em B se, e somente se, a cada elemento do conjunto A corresponde um único elemento do conjunto B. Assim sendo, temos que : Domínio da função D(f)=A O domínio, é o conjunto que contem todos os elementos x, para os quais a função deve ser definida. Contradomínio da função CD(f)=B O contradomínio, é o conjunto que contem os elementos que podem ser relacionados a elementos do domínio. Imagem da função Im(f)B O conjunto imagem, é um subconjunto do contradomínio.
- 7. Função injetora Se para quaiquer elementos distintos do conjunto A(x≠ X) correspondem elementos distintos do conjunto B (y≠ y).
- 8. Função sobrejetora Se o conjunto imagem é igual ao conjunto B, Im(f)=B.
- 9. Função bijetora Se, ao mesmo tempo, é injetora e sobrejetora.
- 10. Domínio de uma função real 1º caso: Quando a variável aparece no denominador de uma fração. Condição: o denominador de uma fração deve ser diferente de zero. 2º caso: Quando a variável aparece no radicando de um radical de índice par. Condição: o radicando de um radical de índice par deve ser um número maior ou igual a zero. 3º caso: Quando a variável aparece no radicando de um radical de índice par e esse radical está no denominador de uma fração. Condição: este caso é a reunião dos dois primeiros; logo, o radicando deve ser maior que zero.
- 11. Função inversa Considerando a função f:A B bijetora, chamamos função inversa de f a função g:B A, tal que f(m)=n se e somente se g(n)=m para todo m A e para todo n B. Função composta Considerando as funções f:A B e g:B C, temos que a função composta de g com f é a função g ○ f:A C, sendo (g ○ f)(x)=g[f(x)]
- 12. Resolva as atividades abaixo: 1-)Dadas as funções f(x)=2x+m e g(x)=ax+2 qual a relação que a e m devem satisfazer para que se tenha (fog)(x)=(gof)(x)? 2-)Sejam as funções reais f e g definidas por: e Obtenha as leis que definem fog e gof. 3-)Seja a função dada por: e seja a função dada por ,com, h ≠0 . Nessas condições, g(x) é igual a : a) h b) x c) 2 x d) 2 x + h e) x + h
- 13. Referências Bibliográficas: http://ecalculo.if.usp.br/funcoes/grandezas/exemplos/exemplos.htm http://mathfire.sites.uol.com.br/Funcao.htm http://mathfire.sites.uol.com.br/RelacaoBinaria.htm http://pt.wikipedia.org/wiki/Ficheiro:Injection.svg
- 14. Tutoria: CLEONICE WEBER Aluna: Pollyana de Brito Correa Soares e-mail: [email_address] Instituição:Universidade Federal Fluminense