Eligheor

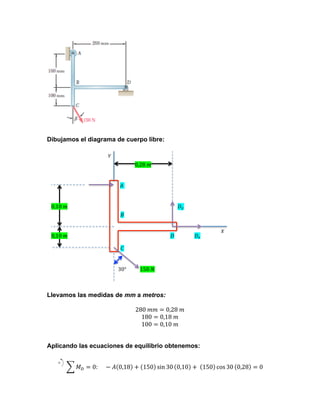
1. Dibujamos el diagrama de cuerpo libre:
!
0,28!!
!!
0,18!!
!!
!
0,10!!
!
!
!
30°
150!!
Llevamos las medidas de mm a metros:
ne Solutions Manual Organization System
280 𝑚𝑚 = 0,28 𝑚
180 = 0,18 𝑚
100 = 0,10 𝑚
on 19.
m:
!!
Aplicando las ecuaciones de equilibrio obtenemos:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0: − 𝐴 0,18 + 150 sin 30 0,10 + 150 cos 30 0,28 = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
∴ C x = −380 N
or
C x = 380 N

2. 21.
OS: Complete Online Solutions Manual Organization System
COSMOS: Complete Online Solutions Manual Organization System
pter 4, Solution 19.
Chapter 4, Solution 19.
e-Body Diagram:
𝐴 =
150 sin 30 0,10 + 150 cos 30 0,28
= 𝟐𝟒𝟑, 𝟕𝟒 𝑵
0,18
(a) From free-body diagram of lever BCD
Free-Body Diagram:
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
(a) From free-body 𝑜 𝐴lever BCD →
diagram of = 244 𝑁
∴ TAB = 300
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
⎛ 2.4 in. ⎞
−⎜
in. From
⎟ A − (0.9 (b))Fsp = 0 free-body diagram of lever BCD
Βx = 0 :
⎝ cosα ⎠
∴ T = 300
ΣFx = 0: 0: 243,74 +300 N ) = 0 30 + 𝐷 = 0 AB
𝐹! = 200 N + Cx + 0.6 ( 150 sin
!
8
(b) From free-body diagram of lever BCD
Fsp =
lb = kx = k (1.2 in.)
∴ C x = −380 N
or
C x = 380 N
cos 30°
ΣFx = 0: 200 N + C + 0.6 ( 300 N ) = 0
𝐷 F 0: C y + − 300 x) = 0
Σ! y==−243,74 0.8 ( 150N sin 30 = −𝟑𝟏𝟖, 𝟕𝟒 𝑵
∴ C x = −380=N
or
k = 7.69800 lb/in.
k 7.70 lb/in. ▹ C x = 380 N
∴ C y = −240 N
or
C y = 240 N
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
0:
or
0:
or
=
𝐹! = 0: 𝐷2 − 150 cos 30 = 0
!
2
2
2
C = C x + C y C = 380 ) N ( 240 ) = 449.44240 N
Then
⎛ 8 lb ⎞
∴ = y ( −240 +
or
Cy = N
( 3 lb ) sin 30° + Bx + ⎜
⎟=0
⎝ cos30° ⎠
C
𝐷!⎛ = ⎞ 1502 cos 240 = 𝟏𝟐𝟗, 𝟗𝟎𝟒 𝑵
− 30 ⎞2
C 1 y 2 = C y =⎛
) 32240 )2
and Then θ = tan −=⎜ C x⎟ + tan −1 ⎜ ( 380⎟ =+ ( .276° = 449.44 N
⎜C ⎟
Bx = −10.7376 lb
⎝ − 380 ⎠
⎝ x⎠
⎛ Cy ⎞
⎛ − 240 ⎞ C = 449 N
− ( 3 lb ) cos 30° + B y = 0
or = 32.276°
32.3° ▹
and
θ = tan −1 ⎜ ⎟ = tan −1 ⎜
⎟
⎜C ⎟
!
! ⎝ x ⎠
⎝ − 380 ⎠ 129,904 ! = 𝟑𝟒𝟒, 𝟐𝟎 𝑵
!+
∴ 𝐷 = 𝐷! + 𝐷! = −318,74
By = 2.5981 lb
or C = 449 N
32.3° ▹
2
2
−10.7376 ) + ( 2.5981) = 11.0475 lb, and
(
𝐷
129,904
2.5981
= tan −1
= 13.6020°
10.7376
𝑦 𝜃 = tan!!
!
𝐷!
= tan!!
𝑜 𝐷 B = 11.05 lb
= 344 𝑁
s: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
Clausen, David Mazurek, Phillip J. Cornwell
mpanies.
Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
7 The McGraw-Hill Companies.
Vector Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
© 2007 The McGraw-Hill Companies.
−318,74
13.60° ▹
𝜃 = 22,2°
= −𝟐𝟐, 𝟏𝟕𝟒°

3. Dibujamos el diagrama de cuerpo libre:
!!
!!
2!
+
!
os
!c
!!
!
!!
!
!!
!!
!!
!!
OS: Complete Online Solutions Manual Organization System
!
!
pter 4, Solution 19.
e-Body Diagram:
Aplicando las ecuaciones de equilibrio obtenemos:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0: 𝑇 2𝑎 + 𝑎 cos 𝜃 − 𝑇𝑎 + 𝑃𝑎 = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
𝑷
𝑇=
(𝑎)
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
𝟏 + 𝐜𝐨𝐬 𝜽
∴ C x = −380 N
or
C x = 380 N
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
∴ C y = −240 N
or
C y = 240 N

4. Free-Body Diagram:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 0: 𝐶 x− 0.6 ( 300 = )0= 0
𝐹! = 200 N + C + 𝑇 sin 𝜃 N
!
∴ C x = −380 N
or
C x = 380 N
COSMOS: Complete Online Solutions Manual Organization System
𝐶 = 𝑻 + 0.8 ( 300 N
ΣFy =!0: C y 𝐬𝐢𝐧 𝜽 (𝑏)) = 0
∴ C y = −240 N
C y = 240 N
or
De la
2 (b)
2
Chapter 4, Solution 19. ecuación (a) en la ecuación+ C y se tiene2que: )2 = 449.44 N
C = Cx
= ( 380 ) + ( 240
Then
Free-Body Diagram:
⎛ C𝑷 ⎞ 𝐬𝐢𝐧 𝜽 −1 ⎛ − 240 ⎞
y
(𝑐) = 32.276°
⎟ = tan ⎜
⎟
𝟏 ⎟
C x+ 𝐜𝐨𝐬 𝜽⎝ − 380 ⎠
⎠
⎝
(a) From free-body diagram of lever BCD
or C = 449 N
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
tan −1 ⎜
θ = 𝐶! = ⎜
and
𝐹! = 0: 𝐶! + 𝑇 + 𝑇 cos 𝜃 − 𝑃 = 0
32.3° ▹
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
𝐶! = 𝑷 − 𝑻 𝟏 + 𝐜𝐨𝐬 𝜽 (𝑑)
∴ C x = −380 N
C x = 380 N
or
Σ ecuación (d) ( 300 N ) = 0
De la ecuación (a) en laFy = 0: C y + 0.8se tiene que:
∴ C y = −240 N
C y = 240 N
or
Then
2
2
2
C = 𝐶C x= 𝑃y− 𝑃 ( 380 )cos (𝜃 = 0= 449.44 N
+ C 2 = 1 + + 240 )
!
and
⎛ Cy ⎞
⎛ − 240 ⎞
θ = tan ⎜ ⎟ = tan −1 ⎜
⎟
⎜ 𝐶! = 0 , 𝐶 = ⎟ =!32.276°
⎝ − 380 ⎠ 𝐶
⎝ Cx ⎠
1 + cos 𝜃
−1
or C = 449 N
32.3° ▹
𝑷 𝐬𝐢𝐧 𝜽
𝐶 =
(𝑒)
𝟏 + 𝐜𝐨𝐬 𝜽
𝑃𝑎𝑟𝑎 𝜃 = 60° 𝑎 𝑡𝑟𝑎𝑣𝑒𝑠 𝑑𝑒𝑙 𝑒𝑛𝑢𝑛𝑐𝑖𝑎𝑑𝑜
De la ecuación (a) se tiene que:
𝑇=
𝑃
𝑃
𝑃
𝟐
=
=
=
1
1 + cos 𝜃
1 + cos 60
𝟑
1 + 2
Vector Mechanics for Engineers:ecuación (e) se tiene que: E. Russell Johnston, Jr.,
De la Statics and Dynamics, 8/e, Ferdinand P. Beer,
Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
© 2007 The McGraw-Hill Companies.
𝐶 =
𝑷
𝑃 sin 𝜃
𝑃 sin 60
𝑃 0,87
=
=
= 𝟎, 𝟓𝟖 𝑷
1
1 + cos 𝜃
1 + cos 60
1 + 2