improper integrals

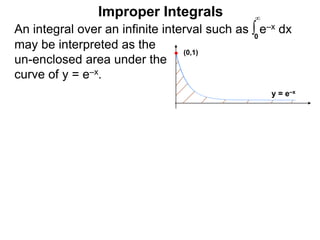
1. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
(0,1)
y = e–x

2. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
Likewise ∫ 1/x dx may be
viewed as the un-enclosed
area under the curve of y = 1/x.
0
1
(0,1)
y = e–x
y = 1/x(1,1)

3. Improper Integrals
An integral over an infinite interval such as ∫ e–x dx
may be interpreted as the
un-enclosed area under the
curve of y = e–x.
0
∞
Likewise ∫ 1/x dx may be
viewed as the un-enclosed
area under the curve of y = 1/x.
0
1
(0,1)
y = e–x
Definite integrals of continuous
functions over infinite intervals (a, ∞)
(–∞, a), or (–∞, ∞), such as ∫ e–x dx,
y = 1/x(1,1)
0
∞
or integrals of unbounded continuous functions
such as ∫ 1/x dx are called improper integrals.0
1

4. Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).

5. ∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

6. Example A. Find ∫0
∞
e–x dx
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

7. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x|
0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

8. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡

9. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a

10. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
–∞
0

11. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
∫
0
cos(x)dx = sin(x) |
–∞
0
–∞ –∞
0

12. Example A. Find ∫0
∞
e–x dx
∫0
∞
e–x dx = –e–x| = lim (–e–x) – (–e0) = 1
x ∞0
∞
∫a
∞
lim f(x) dx = F(x)| ≡ lim F(u) – F(a)∫a
u
u ∞ u ∞a
∞
Improper Integrals
Let f(x) be a continuous function defined for a ≤ x
and F(x) is an antiderivative of f(x).
We define the improper (definite) integral
f(x) dx ≡
Similarly for a continuous function f(x) where x ≤ a,
we define the improper (definite) integral
∫–∞
lim f(x) dx = F(x)| ≡ lim F(a) – F(u)∫u
a
u –∞ u –∞
a
–∞
f(x) dx ≡
a
Example B. Find ∫ cos(x)dx
∫
0
cos(x)dx = sin(x) | = lim sin(0) – sin(x) which is UDF.
x –∞
–∞
0
–∞ –∞
0

13. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
a
b
Improper Integrals
x a

14. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
a
b
Improper Integrals
x a

15. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The green area
under y = x–1 is ∞.
The blue area
under y = x–1/2 is 2.

16. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.

17. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

18. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

19. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) |
1
0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

20. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

21. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
If the improper integral exists, we say it converges.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

22. Let F(x) be an antiderivative of f(x) and lim f(x)  ∞.
We define
x a
∫a
b
f(x) dx = F(x)| ≡ F(b) – lim F(x)
Example C. a. Find ∫0
1
x–1/2 dx.
∫0
1
x–1/2 dx = 2x1/2 |
1
0
x 0
b. Find ∫0
1
x–1 dx.
∫0
1
x–1 dx = In(x) | = 0 – lim In(x) = 0 – (–∞) = ∞
1
0 x 0
If the improper integral exists, we say it converges.
If the improper integral fails to exist or it´s infinite,
we say it diverges.
a
b
Improper Integrals
x a
y = x–1/2
y = x–1
(1,1)
The blue area
under y = x–1/2 is 2.
The green area
under y = x–1 is ∞.
= 2 – lim (2x1/2) = 2

23. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
In the situations that we can’t find the anti-derivative
F(x) or the numerical answers, the next question is
to determine if the integrals converge or diverge
by comparing them to other known integrals.
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

24. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
u∞
= lim F(u) – F(–u).u∞

25. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
1/(1 + x2)dx
u∞
= lim F(u) – F(–u).u∞

26. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x

27. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u

28. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

29. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

30. Let f(x) be a continuous function defined for all x’s,
and F´(x) = f(x), we define the improper integral
∫ f(x)dx ≡ lim
Improper Integrals
–∞
∞
∫f(x) dx
–u
u
In the situations that we can’t find the anti-derivative
F(x) or the numerical answers, the next question is
to determine if the integrals converge or diverge
by comparing them to other known integrals.
Find ∫Example D.
–∞
∞
∫ 1/(1 + x2) dx
–∞
∞
= lim tan–1(u) – tan–1(–u)
= π/2 + π/2 = π.
u ∞
y = 1/(1 + x2)1/(1 + x2)dx
x
u∞
= lim F(u) – F(–u).u∞
–x
= lim tan–1(x) l–u
u
u ∞

31. The Floor Principle
Improper Integrals
The Ceiling Principle
Here are two basic comparison-principles.

32. The Floor Principle
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
Here are two basic comparison-principles.

33. The Floor Principle
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

34. The Floor Principle
If f(x) ≥ g(x) ≥ 0 and g(x) dx = ∞, then f(x) dx = ∞.∫a
b
∫a
b
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

35. The Floor Principle
If f(x) ≥ g(x) ≥ 0 and g(x) dx = ∞, then f(x) dx = ∞.∫a
b
∫a
b
y = f(x)
y = g(x)∞
Improper Integrals
The Ceiling Principle
If f(x) ≥ g(x) ≥ 0 and f(x) dx = N converges
then g(x) dx converges also (a and b could be ±∞.)
∫a
b
∫a
b
y = f(x)
y = g(x)
N
Here are two basic comparison-principles.

36. Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals

37. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals

38. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
y = 1/x

39. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
∫
1
0
x
1
dx = Ln(x)| = ∞
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
1
0
y = 1/x

40. The important function which serves as a "boundary"
between divergent and convergent integrals is y = 1/x.
Note that no conclusion may be drawn if f ≥ g ≥ 0 with
g dx < ∞ finite, or with f dx = ∞.∫a
b
∫a
b
Improper Integrals
∫
1
0
x
1
dx = Ln(x)| = ∞
(1, 1)
Both of the following integrals diverge
∫1
∞
x
1
dx = Ln(x)| = ∞
1
∞
1
0
y = 1/x
The functions y = 1/xp
are called p-functions
and y = 1/x serves as the
“boundary” between the
convergent and divergent p-functions.

41. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
diverges for p ≤ 1.
We can verify the following theorems easily.

42. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.

43. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)

44. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
diverges for p ≤ 1.
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.

45. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
0 1
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
Area < ∞
y = 1/x1/2
y = 1/x
y = 1/x1/3
diverges for p ≤ 1.
(1, 1)
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.

46. Theorem (p–function) ∫1
xp
1
∞
dx converges for p > 1,A.
Improper Integrals
0 1
(1, 1)
y = 1/x
y = 1/x2
y = 1/x3
1
Area < ∞
Area < ∞
y = 1/x1/2
y = 1/x
y = 1/x1/3
diverges for p ≤ 1.
(1, 1)
We can verify the following theorems easily.
(So ∫1 x1.01
1∞
dx converges.)
∫ xp
1
dx converges for p < 1,B.
0
1
diverges for p ≥ 1.
(So ∫ x0.99
1
dx converges.)
0
1

47. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.

48. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,

49. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx∫
∞
1
∫
∞
1

50. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1

51. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
For 0 < x < 1,

52. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1

53. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1
so 2/(x3 + x2)dx >∫0
1
∫0
1
1/x2 dx

54. Improper Integrals
∫
Example E. Determine if the integral converges or
diverges using the comparison principle.
∞
1
1/(1 + x + x3/2) dxa.
∫0
1
2/(x3 + x2 )dxb.
Since 1/(1 + x + x3/2) < 1/x3/2 for 1 < x,
so 1/(1 + x + x3/2) dx < 1/x3/2 dx < ∞ converges.∫
∞
1
∫
∞
1
2
x3 + x2 = 2
x2(x + 1)
>
1
x2For 0 < x < 1,
1
so 2/(x3 + x2)dx >∫0
1
∫0
1
1/x2 dx = ∞ and it diverges.

55. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
Improper Integrals

56. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
That is ∫1
∞
f(x) dx
= 1/2 + 1/4 + 1/8 + 1/16.. = 1
∫1
2
f(x) dx + ∫2
3
f(x) dx + ∫3
4
f(x) dx +. .=
Improper Integrals

57. An infinite series such as 1/2 + 1/4 + 1/8 + 1/16.. (= 1)
may be viewed as the area under the following
“multi–rule” function f(x) where
f(x) = 2–n for n ≤ x < n + 1
where n = 1, 2, 3,..
1
y = f(x)
2 3 4
y
5
That is ∫1
∞
f(x) dx
= 1/2 + 1/4 + 1/8 + 1/16.. = 1
∫1
2
f(x) dx + ∫2
3
f(x) dx + ∫3
4
f(x) dx +. .=
In the next section, we establish the
relation between summing series
versus integrating functions,
i.e. the discrete vs. the continuous.
Improper Integrals