QUINTIC
•
1 gefällt mir•1,523 views
This document discusses solving quintic (degree 5) polynomial equations. It presents the general form of a quintic polynomial and methods for finding its roots, including using the factorization of polynomials and representations of the roots in terms of radicals. It also discusses representing functions as tensors and decomposing them into products of simpler tensors.
Melden
Teilen
Melden
Teilen
Downloaden Sie, um offline zu lesen
Empfohlen
Empfohlen
Arithmetic Progressions and the Construction of Doubly Even Magic Squares

Arithmetic Progressions and the Construction of Doubly Even Magic SquaresLossian Barbosa Bacelar Miranda
Weitere ähnliche Inhalte
Was ist angesagt?
Arithmetic Progressions and the Construction of Doubly Even Magic Squares

Arithmetic Progressions and the Construction of Doubly Even Magic SquaresLossian Barbosa Bacelar Miranda
Was ist angesagt? (17)
Arithmetic Progressions and the Construction of Doubly Even Magic Squares

Arithmetic Progressions and the Construction of Doubly Even Magic Squares
Ähnlich wie QUINTIC
Ähnlich wie QUINTIC (20)
IIT-JEE Mains 2017 Online Mathematics Previous Paper Day 2

IIT-JEE Mains 2017 Online Mathematics Previous Paper Day 2
Boundary value problem and its application in i function of multivariable

Boundary value problem and its application in i function of multivariable
jhkl,l.มือครูคณิตศาสตร์พื้นฐาน ม.4 สสวท เล่ม 2fuyhfg

jhkl,l.มือครูคณิตศาสตร์พื้นฐาน ม.4 สสวท เล่ม 2fuyhfg
IIT-JEE Mains 2017 Online Mathematics Previous Paper Day 1

IIT-JEE Mains 2017 Online Mathematics Previous Paper Day 1
Mehr von Junpei Tsuji
Mehr von Junpei Tsuji (20)
Kürzlich hochgeladen
Mattingly "AI & Prompt Design: Structured Data, Assistants, & RAG"

Mattingly "AI & Prompt Design: Structured Data, Assistants, & RAG"National Information Standards Organization (NISO)
Mattingly "AI & Prompt Design: The Basics of Prompt Design"

Mattingly "AI & Prompt Design: The Basics of Prompt Design"National Information Standards Organization (NISO)
Kürzlich hochgeladen (20)
Presentation by Andreas Schleicher Tackling the School Absenteeism Crisis 30 ...

Presentation by Andreas Schleicher Tackling the School Absenteeism Crisis 30 ...
18-04-UA_REPORT_MEDIALITERAСY_INDEX-DM_23-1-final-eng.pdf

18-04-UA_REPORT_MEDIALITERAСY_INDEX-DM_23-1-final-eng.pdf
Mattingly "AI & Prompt Design: Structured Data, Assistants, & RAG"

Mattingly "AI & Prompt Design: Structured Data, Assistants, & RAG"
Privatization and Disinvestment - Meaning, Objectives, Advantages and Disadva...

Privatization and Disinvestment - Meaning, Objectives, Advantages and Disadva...
Measures of Central Tendency: Mean, Median and Mode

Measures of Central Tendency: Mean, Median and Mode
TataKelola dan KamSiber Kecerdasan Buatan v022.pdf

TataKelola dan KamSiber Kecerdasan Buatan v022.pdf
Call Girls in Dwarka Mor Delhi Contact Us 9654467111

Call Girls in Dwarka Mor Delhi Contact Us 9654467111
Mattingly "AI & Prompt Design: The Basics of Prompt Design"

Mattingly "AI & Prompt Design: The Basics of Prompt Design"
Z Score,T Score, Percential Rank and Box Plot Graph

Z Score,T Score, Percential Rank and Box Plot Graph
Separation of Lanthanides/ Lanthanides and Actinides

Separation of Lanthanides/ Lanthanides and Actinides
Introduction to ArtificiaI Intelligence in Higher Education

Introduction to ArtificiaI Intelligence in Higher Education
QUINTIC
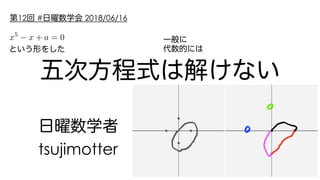
- 1. tsujimotter 12 # 2018/06/16 x5 x + a = 0
- 2. x5 x + a = 0
- 3. x2 + ax + b = 0 x = a ± p a2 4b 2
- 4. x = a ± p a2 4b 2 x2 1 = a2 4b x2 = a 2 + x1 2
- 5. xk2 2 = f2(a, x1) xk1 1 = f1(a) xkN N = fN (a, x1, . . . , xN 1) ... x5 N xN + a = 0 x5 x + a = 0
- 6. a = 0 x5 x = (x 1)(x + 1)x(x i)(x + i) = 0 i i 1 10 x5 x + a = 0
- 7. x5 x + a = 0a
- 8. x5 x + a = 0a
- 9. x5 x + a = 0a
- 10. x5 x + a = 0a
- 11. x5 x + a = 0a
- 12. 1 (i) 1 2 2
- 13. 2 3 1 (ii) 1, 2, 3
- 15. • n 5 • N • N xN • xN •
- 16. 1 2 3 4 5 1 2 3 4 5 (2 3 1 4 5)
- 17. 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 = (2 3 1 4 5) = (1 4 3 2 5) = (4 3 1 2 5)
- 18. [↵, ] := ↵ ↵ 1 1
- 19. n 5 ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s]
- 20. ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s]
- 21. ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s] ↵1 = [↵1,1, ↵1,2][↵1,3, ↵1,4] · · · [↵1,2t 1, ↵1,2t]
- 22. ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s] ↵1 = [↵1,1, ↵1,2][↵1,3, ↵1,4] · · · [↵1,2t 1, ↵1,2t] ↵1,1 = [↵1,1,1, ↵1,1,2] · · · [↵1,1,2r 1, ↵1,1,2r]
- 23. ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s] ↵1 = [↵1,1, ↵1,2][↵1,3, ↵1,4] · · · [↵1,2t 1, ↵1,2t] ... ↵1,...,1 = [↵1,1,...,1, ↵1,1,...,2] · · · [↵1,1,...,2z 1, ↵1,1,...,2z] ↵1,1 = [↵1,1,1, ↵1,1,2] · · · [↵1,1,2r 1, ↵1,1,2r]
- 24. ↵0 = [↵1, ↵2][↵3, ↵4] · · · [↵2s 1, ↵2s] ↵1 = [↵1,1, ↵1,2][↵1,3, ↵1,4] · · · [↵1,2t 1, ↵1,2t] ... ↵1,...,1 = [↵1,1,...,1, ↵1,1,...,2] · · · [↵1,1,...,2z 1, ↵1,1,...,2z] ↵1,1 = [↵1,1,1, ↵1,1,2] · · · [↵1,1,2r 1, ↵1,1,2r]
- 25. 0 `0 = [`1, `2][`3, `4] · · · [`2s 1, `2s] `1 = [`1,1, `1,2][`1,3, `1,4] · · · [`1,2t 1, `1,2t] `1,1 = [`1,1,1, `1,1,2] · · · [`1,1,2r 1, `1,1,2r] `1,...,1 = [`1,1,...,1, `1,1,...,2] · · · [`1,1,...,2z 1, `1,1,...,2z] ...
- 26. xk2 2 = f2(a, x1) xk1 1 = f1(a) xkN N = fN (a, x1, . . . , xN 1) ... x5 N xN + a = 0
- 27. xk2 2 = f2(a, x1) xk1 1 = f1(a) xkN N = fN (a, x1, . . . , xN 1) ... x5 N xN + a = 0 a
- 28. xk1 1 = f1(a) x1, x1⇣, x1⇣2 , · · · , x1⇣k1 1
- 29. xk1 1 = f1(a) x1, x1⇣, x1⇣2 , · · · , x1⇣k1 1 `1 x1 7! x1⇣m1 x1 7! x1⇣m2 `2 [`1, `2] = `1`2` 1 1 ` 1 2
- 30. xk1 1 = f1(a) x1, x1⇣, x1⇣2 , · · · , x1⇣k1 1 x1 `1 x1 7! x1⇣m1 x1 7! x1⇣m2 `2 [`1, `2] = `1`2` 1 1 ` 1 2 x1 `1 7 ! x1⇣m1 `2 7 ! x1⇣m1+m2 ` 1 1 7 ! x1⇣m2 ` 1 2 7 ! x1
- 31. x1
- 32. x1 x2
- 33. x1 N-1 xN-1 N xN
- 34. N xN xN
- 35. N xN xN
- 36. • n 5 • N • N xN • xN •
- 37. D. S. (2012)
