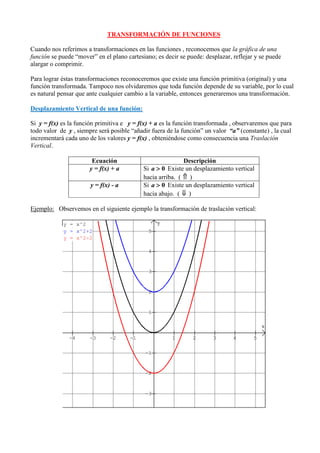
1. TRANSFORMACIÓN DE FUNCIONES
Cuando nos referimos a transformaciones en las funciones , reconocemos que la gráfica de una
función se puede “mover” en el plano cartesiano; es decir se puede: desplazar, reflejar y se puede
alargar o comprimir.
Para lograr éstas transformaciones reconoceremos que existe una función primitiva (original) y una
función transformada. Tampoco nos olvidaremos que toda función depende de su variable, por lo cual
es natural pensar que ante cualquier cambio a la variable, entonces generaremos una transformación.
Desplazamiento Vertical de una función:
Si y = f(x) es la función primitiva e y = f(x) + a es la función transformada , observaremos que para
todo valor de y , siempre será posible “añadir fuera de la función” un valor “a” (constante) , la cual
incrementará cada uno de los valores y = f(x) , obteniéndose como consecuencia una Traslación
Vertical.
Ecuación Descripción
y = f(x) + a Si a  0 Existe un desplazamiento vertical
hacia arriba. (  )
y = f(x) - a Si a  0 Existe un desplazamiento vertical
hacia abajo. (  )
Ejemplo: Observemos en el siguiente ejemplo la transformación de traslación vertical:
y = x^2 y
y = x^2+2 5
y = x^2-2
4
3
2
1
x
-4 -3 -2 -1 1 2 3 4 5
-1
-2
-3

2. Desplazamiento Horizontal de una función:
Si y = f(x) es la función primitiva e y = f(x- a) es la función transformada , observaremos que para
todo valor de y , siempre será posible “añadir o retirar dentro de la función” un valor “a” (constante)
obteniéndose como consecuencia una Traslación Horizontal.
Ecuación Descripción
y = f(x - a) Si a  0 Existe un desplazamiento
horizontal a la derecha. (  )
y = f(x + a) Si a  0 Existe un desplazamiento
horizontal a la izquierda. (  )
Ejemplo: Observemos en el siguiente ejemplo la transformación de traslación horizontal:
y = x^2 y
y = (x-2)^2
y = (x+2)^2 6
5
4
3
2
1
x
-4 -3 -2 -1 1 2 3 4 5
-1
-2
Estiramiento o encogimiento Vertical de una función:
Si y = f(x) es la función primitiva e y =a f(x) es la función transformada , observaremos que para
todo valor de y , siempre será posible “multiplicar fuera de la función” un valor “a” (constante)
obteniéndose como consecuencia un Estiramiento o encogimiento Vertical.
Ecuación Descripción
y =a f(x) Si a  1 Existe un Encogimiento Vertical
de la función.
y =a f(x) Si 0  a  1 Existe un Estiramiento
(ensanchamiento) Vertical de la función.

3. Ejemplo: Observemos en el siguiente ejemplo la transformación: Encogimiento o Estiramiento
Vertical.
y = x^2 y
y = 3x^2
y = 0.5x^2 6
5
4
3
2
1
x
-4 -3 -2 -1 1 2 3 4 5
-1
-2
Encogimiento o Alargamiento Horizontal de una función:
Si y = f(x) es la función primitiva e y = f(ax) es la función transformada , observaremos que para
todo valor de y , siempre será posible “multiplicar dentro de la función” un valor “a” (constante)
obteniéndose como consecuencia un Encogimiento o Alargamiento Horizontal.
Ecuación Descripción
y = f(ax) Si a  1 Existe un Encogimiento
Horizontal de la función.
y = f(ax) Si 0  a  1 Existe un Alargamiento
Horizontal de la función.
Ejemplo: Observemos en el siguiente ejemplo la transformación: Encogimiento o Estiramiento
y = sin(x) y
Vertical. y = sin(2x)
y = sin(0.8x)
3
2
1
x
-3 -2 -1 1 2 3 4
-1
-2
-3

4. Simetría respecto a los Ejes de una función:
Si y = f(x) es la función primitiva e y =- f(x) o y = f(-x) es la función transformada , observaremos
que para todo valor de y , siempre será posible “multiplicar fuera o dentro de la función” un valor
“-1” (constante) obteniéndose como consecuencia Simetría respecto a los Ejes X e Y.
Ecuación Descripción
y =- f(x) Existe una Simetría respecto al eje X.
y = f(-x) Existe una Simetría respecto al eje Y.
Ejemplo: Observemos en el siguiente ejemplo la transformación: Simetría o Reflexión.
y = 2^x y
y = -2^x 4
y = 2^-x
3
2
1
x
-4 -3 -2 -1 1 2 3 4 5
-1
-2
-3
-4