Problemes resolts de derivades PAU

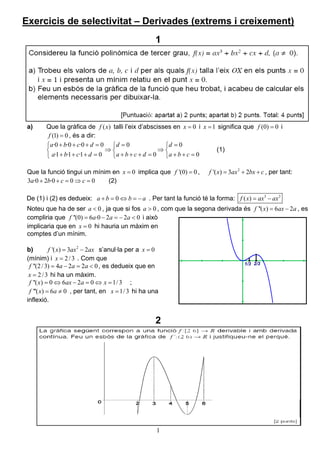
1. 1
Exercicis de selectivitat – Derivades (extrems i creixement)
1
a) Que la gràfica de ( )f x talli l’eix d’abscisses en 0x = i 1x = significa que (0) 0f = i
(1) 0f = , és a dir:
·0 ·0 ·0 0 0 0
·1 ·1 ·1 0 0 0
a b c d d d
a b c d a b c d a b c
+ + + = = =  
⇒ ⇒  
+ + + = + + + = + + =  
(1)
Que la funció tingui un mínim en 0x = implica que '(0) 0f = , 2
'( ) 3 2f x ax bx c= + + , per tant:
3 ·0 2 ·0 0 0a b c c+ + = ⇒ = (2)
De (1) i (2) es dedueix: 0a b b a+ = ⇔ = − . Per tant la funció té la forma: 3 2
( )f x ax ax= −
Noteu que ha de ser 0a < , ja que si fos 0a > , com que la segona derivada és ''( ) 6 2f x ax a= − , es
compliria que ''(0) 6 ·0 2 2 0f a a a= − = − < i això
implicaria que en 0x = hi hauria un màxim en
comptes d’un mínim.
b) 2
'( ) 3 2f x ax ax= − s’anul·la per a 0x =
(mínim) i 2/3x = . Com que
''(2/3) 4 2 2 0f a a a= − = < , es dedueix que en
2/3x = hi ha un màxim.
''( ) 0 6 2 0 1/3f x ax a x= ⇔ − = ⇔ = ;
'''( ) 6 0f x a= ≠ , per tant, en 1/3x = hi ha una
inflexió.
2
1/3 2/3

2. 2
Observant el dibuix es veu que en l’interval (2, 3)
les tangents a la gràfica tenen pendent positiu, per
tant, 'f és positiva. Això també passa en l’interval
(5, 6) . En canvi, en l’interval (3, 5) la derivada ha
de ser negativa.
En els punts 3x = i 5x = la funció hi té extrems,
per tant, la derivada s’hi anul·la: '(3) '(5) 0f f= =
En el punt 4x = la funció hi té una inflexió i passa
de convexa a còncava; per tant la derivada passa
de decréixer a créixer i hi té, per tant, un mínim.
La gràfica de '( )f x pot ser com la de la figura
3
a) 1 2
2 3
12
( ) 1 6 '( )
a
f x a x x f x
x x
− −
= + + ⇒ = − − Si en 3x = hi ha un extrem s’ha de complir:
'(3) 0f = , és a dir: 2 3
12
0 3 12 0
3 3
a
a− − = ⇒ − − = ⇒ 4a = −
b) 2 3
2 3 3 4 3 4
4 12 8 36 8 36 12
'( ) 4 12 ''( ) ''(3) 0
3 3 81
f x x x f x f
x x x x
− −
= − = − ⇒ = − + ⇒ = − + = > , per tant es
tracta d’un mínim relatiu.
4
a) Perquè hi hagi un extrem relatiu en 3x = s’ha de complir: '(3) 0f =
3 2
6 4
3 ( ) 2 3
'( )
x x x a x a
f x
x x
− + − −
= =
6 3
'(3) 0 0
81
a
f
− −
= ⇒ = ⇒ 2a = −
b) 4
2 6
'( )
x
f x
x
− +
= Si 3x < es compleix: '( ) 0f x > , per tant ( )f x és creixent en ( , 3)−∞
Si 3x > es compleix: '( ) 0f x < , per tant ( )f x és decreixent en (3, )+∞
3 4 5

3. 3
3
2
( )
x
f x
x
−
= Com que
0
( )
x
lím f x
→
= ∞ , la funció té una asímptota vertical d’equació: 0x =
Com que ( ) 0
x
lím f x
→ ± ∞
= (grau del numerador més petit que el del denominador), la funció té una
asímptota horitzontal d’equació: 0y = (Les asímptotes són els eixos de coordenades)
5
( )
( ) ( )
22 2
2 2
(2 1)( 1) 66 2 7
'( ) ''( )
1 1 1
x x x xx x x x
f x f x
x x x
+ + − + −+ − + +
= ⇒ = =
+ + +
En els extrems de la funció la derivada s’anul·la. Busquem els punts singulars de ( )f x :
2
2 36
'( ) 0 0 6 0
21
x x
f x x x x
x
−+ −
= ⇔ = ⇒ + − = ⇔ = 
+ 
Calculem la segona derivada en aquests punts:
( )
2
9 6 7 10
''( 3) 0
93
f
− +
− = = >
−
Per tant, la funció té un mínim relatiu en 3x = −
2
4 4 7 15
''(2) 0
2 4
f
+ +
= = > Per tant, la funció té un altre mínim relatiu en 2x =
6
Calculem la derivada de la funció: ( )2 2
' 4 2 ( ) 3 2 4y x x x a x a x= − + + = + −
Si la funció té un màxim relatiu en 1/3x = − , en aquest punt la derivada ha de valer 0 :
2
1 1 1 2
3 2 4 0 4 0
3 3 3 3
a
a
   
− + − − = ⇒ − − = ⇒   
   
11
2
a = −
L’altre extrem (el mínim) s’ha de donar en l’altre punt en què la derivada s’anul·la:
2
' 3 11 4y x x= − − ; 2 411 121 48
' 0 3 11 4 0
1/36
y x x x
± +
= ⇔ − − = ⇔ = = 
−
Per tant, l’abscissa del
mínim és 4x =
7

4. 4
a) 2 3
3 2(3 )
'( ) 1 ; ''( )
a a
f x f x
x x
− −
= − = En els punts en què la funció té extrems la derivada ha
de valer 0
2
2
3
'( ) 0 1 0 3 3
a
f x a x x a
x
−
= ⇔ − = ⇒ − = ⇒ = ± − (1)
Si 3a = la funció és: ( )f x x= (excepte per a 0x = ) i, per tant, no té extrems.
Si 3a > l’equació (1) no té solucions (radicand negatiu), per tant, la funció no té extrems.
Si 3a < l’equació (1) té dues solucions, una de positiva: 1 3x a= + − i una de negativa:
2 3x a= − − Es comprova que 1''( ) 0f x > i 2''( ) 0f x < , per tant la funció té un màxim en 2x i
un mínim en 1x
b) Si 3a = la funció coincideix amb la recta y x= (excepte en 0x = ) i, per tant és creixent en
tot el seu domini.
Si 3a > la derivada és: 2 2
3 3
'( ) 1 1 0
a a
f x
x x
− −
= − = + > per a qualsevol 0x ≠ ; per tant, en
aquest cas la funció també és creixent en tot el seu domini.
Si 3a < ja hem vist que la funció té màxim i mínim, per tant en algun interval és decreixent.
8
a)
2
2 2
2 1 2/ 1
( )
2 1 2 1/ 2x x x
x x x
lím f x lím lím
x x→±∞ →±∞ →±∞
− −
= = =
+ +
Per tant, la funció té una asímptota horitzontal
(per la dreta i per l’esquerra) d’equació: 1/ 2y =
Si té asímptota horitzontal ja no en pot tenir d’obliqües.
Com que el denominador de ( )f x no s’anul·la per a cap valor de x , tampoc no hi ha
asímptotes verticals.
b)
( ) ( )
( ) ( )
2 2 2
2 22 2
(2 2) 2 1 4 2 4 2 2
'( )
2 1 2 1
x x x x x x x
f x
x x
− + − − + −
= =
+ +
( )
2
2
22
1/ 24 2 2 1 9
'( ) 0 0 2 1 0
142 1
x x
f x x x x
x
+ − − ±
= ⇔ = ⇔ + − = ⇔ = = 
−+
Noteu que el signe de la derivada només depèn del numerador ja que el denominador és
positiu per a qualsevol valor de x . És fàcil comprovar que:
Si 1x < − llavors '( ) 0f x > , per tant ( )f x és creixent estrictament en ( , 1)−∞ −
Si 1 1/ 2x− < < llavors '( ) 0f x < , per tant ( )f x és decreixent estrictament en ( 1, 1/ 2)−
Si 1/ 2x > llavors '( ) 0f x > , per tant ( )f x és creixent estrictament en (1/ 2, )+∞
Es dedueix que la funció té un màxim relatiu en 1x = − i un mínim relatiu en 1/ 2x =

5. 5
c) i d)
La funció ( )g x té màxim allà on ( )f x té mínim i viceversa. (Per a obtenir la gràfica de ( )g x cal
“girar” la de ( )f x respecte de l’eix d’abscisses i traslladar-la tres unitats cap a dalt.)
9
a) 2
'( ) 3 3 6f x x x= − − ; Els extems relatius es donen en punts en què la derivada val 0 :
2 2 2
'( ) 0 3 3 6 0 2 0
1
f x x x x x x

= ⇔ − − = ⇔ − − = ⇔ = 
−
(punts singulars)
''( ) 6 3f x x= − ; ''(2) 9 0f = > per tant hi ha un mínim relatiu en 2x =
''( 1) 9 0f − = − < per tant hi ha un màxim relatiu en 1x = −
3 23
(2) 2 ·2 6·2 3 13
2
f = − − − = − 3 23 1
( 1) ( 1) ·( 1) 6·( 1) 3
2 2
f − = − − − − − − =
b) Si la funció ( )f x tingués, per exemple,
quatre arrels (quatre punts en què
tallaria l’eix d’abscisses), com que és
contínua i derivable, entre cada dues
arrels hi hauria un extrem i n’hi hauria
tres com a mínim, en comptes dels
dos que hem trobat.
Que la funció té tres arrels es dedueix
del teorema de Bolzano:
( )f x és contínua en [ ]2, 1− − i
( 2) 0f − < i ( 1) 0f − > , per tant existeix un punt c entre 2− i 1− tal que ( ) 0f c = .
Anàlogament es pot raonar en els intervals (per exemple) [ ]1, 0− i [ ]2, 4
-1
1/2
( )f x
-1
1/2
( )g x
2-1

6. 6
10
a) Calculem-ne l’asímptota obliqua: y m x n= +
2
2
( )
1
x x
f x x
lím lím m
x x a x→±∞ →±∞
= = =
+
(pendent de l’asímptota)
( )
2
( )
x x x
x a x
lím f x mx lím x lím a n
x a x a→±∞ →±∞ →±∞
   −
− = − = = − =   
+ +  
(ordenada a l’origen)
Per tant, l’asímptota (per la dreta i per l’esquerra) és: y x a= − . De l’enunciat es dedueix
que 2a = −
b)
2
( )
2
x
f x
x
=
−
Domini: }{ 2 0Dom f x x= ∈ − ≠ = { }2−
Interseccions amb eixos: (0) 0f = → (0, 0)
( ) 0 0 (0, 0)f x x= ⇒ = →
Creixement i extrems:
2 2
2 2
2 ( 2) 4
'( )
( 2) ( 2)
x x x x x
f x
x x
− − −
= =
− −
2
2
04
'( ) 0 0
4( 2)
x x
f x x
x
−
= ⇔ = ⇔ = 
− 
(punts singulars)
És fàcil comprovar que:
Si 0x < la derivada és positiva, per tant, la funció és creixent en ( , 0)−∞
Si 0 4x< < ( 0x ≠ ) la derivada és negativa, per tant, la funció és decreixent en (0, 2) i
(2, 4)
Si 4x > la derivada és positiva, per tant, la funció és creixent en (4, )+∞
Es dedueix que té un màxim relatiu en 0x = , i un mínim relatiu en 4x =
40

7. 7
11
a) Domini de ( )f x : { } { }2
8 0 0, 8Dom f x x x= ∈ − ≠ = −
Asímptotes verticals:
0
( )
x
lím f x
→
= ∞ i
8
( )
x
lím f x
→
= ∞ , per tant hi ha dues asímptotes
verticals d’equacions: 0x = i 8x =
Asímptotes horitzontals: ( ) 0
x
lím f x
→±∞
= (numerador de grau més petit que el denominador),
per tant hi ha una asímptota horitzontal (per la dreta i per l’esquerra) d’equació: 0y =
Com que n’hi ha d’horitzontals no n’hi pot haver d’obliqües.
b) Com que el numerador és positiu, el signe de la funció només depèn del denominador
2
8 (8 )x x x x− = −
És fàcil veure que:
Si 0x < el denominador és negatiu, per tant ( ) 0f x < en ( , 0)−∞
Si 0 8x< < el denominador és positiu, per tant ( ) 0f x > en (0, 8)
Si 8x > el denominador és negatiu, per tant ( ) 0f x < en (8, )+∞
c)
( )
22
2 8
'( )
8
x
f x
x x
−
=
−
Aquesta derivada s’anul·la en 4x = (punt singular). El seu signe
depèn del numerador (observeu que el denominador sempre és positiu)
Si 4x > la derivada és positiva, per tant ( )f x és creixent en (4, 8) i (8, )+∞
Si 4x < la derivada és negativa, per tant ( )f x és decreixent en ( , 0)−∞ i (0, 4)
Es dedueix que hi ha un mínim relatiu
en 4x =
4 80
0 4 8

8. 8
12
a) Asímptotes verticals (només poden estar en els punts en què s’anul·la el denominador):
1
( ' )
( )
( )x
per l esquerra
lím f x
per la dreta→−
−∞
= 
+∞
, per tant hi ha una asímptota vertical d’equació: 1x = −
Asímptotes horitzontals:
2
( 1) 1
( )
1 (1 1/ ) 1 1/x x x x
x x x x x
lím f x lím lím lím
x x x x→+∞ →+∞ →+∞ →+∞
− − −
= = = = +∞
+ + +
Anàlogament: ( )
x
lím f x
→−∞
= −∞ per tant, no hi ha asímptotes horitzontals.
Asímptotes obliqües: y m x n= +
( ) 1 (1 1/ ) 1 1/
1
1 (1 1/ ) 1 1/x x x x
f x x x x x
lím lím lím lím m
x x x x x→± ∞ →+∞ →+∞ →+∞
− − −
= = = = =
+ + +
(pendent de l’asímptota)
( )
2
2 2
( ) 2
1 1 1 1/x x x x
x x x
lím f x m x lím x lím lím n
x x x→± ∞ →+∞ →+∞ →+∞
 − − −
− = − = = = − = 
+ + + 
(ordenada a l’origen)
Per tant, hi ha una asímptota obliqua (per la dreta i per l’esquerra) d’equació: 2y x= −
b) i c)
( )2 2
2 2
(2 1)( 1) 2 1
'( )
( 1) ( 1)
x x x x x x
f x
x x
− + − − + −
= =
+ +
Els extrems relatius es donen en punts en què
la derivada val 0 :
2
2
2
1 22 1 2 8
'( ) 0 0 2 1 0
( 1) 2 1 2
x x
f x x x x
x
− ++ − − ± 
= ⇔ = ⇒ + − = ⇔ = = 
+ − −
(punts singulars)
El signe de la derivada depèn del numerador (ja que el denominador és sempre positiu)
És fàcil veure que:
Si 1 2x < − − la derivada és positiva, per tant la funció és creixent en ( ), 1 2−∞ − −
Si 1 2 1 2x− − < < − + (excepte 1x = − ) la derivada és negativa, per tant la funció és
decreixent en ( )1 2 , 1− − − i
( )1, 1 2− − +
Si 1 2x > − + la derivada és positiva, per
tant la funció és creixent en
( )1 2 ,− + +∞
Es dedueix que ( )f x té un màxim en
1 2x = − − i un mínim en 1 2x = − +

9. 9
13
a) 2
'( ) 3 2 ''( ) 6 2f x x x f x x= + = + Els màxims i mínims es troben en punts en què la
derivada s’anul·la: 2 0
'( ) 0 3 2 0
2/3
f x x x x

= ⇔ + = ⇔ = 
−
(punts singulars)
''(0) 2 0f = > , per tant hi ha un mínim relatiu en 0x =
''( 2/3) 2 0f − = − < , per tant hi ha un màxim relatiu en 2/3x = −
(0)f b= 3 2
( 2/3) ( 2/3) ( 2/3)f b− = − + − + =
4
27
b+
b) Si 0b > la gràfica tallarà l’eix d’ordenades en el punt (0, )b , per sobre de l’origen
Si 0b = la gràfica passarà per l’origen de coordenades.
c) Perquè la gràfica en el màxim relatiu sigui
tangent a l’eix d’abscises s’ha de complir:
4
( 2/3) 0 0
27
f b− = ⇔ + = ⇔ 4/ 27b = −
d) A la vista de les gràfiques es dedueix que
si 0b = o 4/ 27b = − l’equació ( ) 0f x =
tindrà dues solucions (una de les quals
serà el màxim o el mínim). Si 0b > o
4/ 27b < − en tindrà només una i si
0
-2/3
0
-2/3
0-2/3

10. 10
4/ 27 0b− < < l’equació tindrà tres solucions.
14
a)
( )
( ) ( ) ( )
2 2 2
2 2 22 2 2
9 2 ( 5) 10 9 10 9
'( )
9 9 9
x x x x x x x
f x
x x x
− − + − − − + +
= = = −
− − −
( )
2
22
2 10·2 9 33
'(2)
252 9
f
+ +
= − = −
−
(pendent de la tangent) ;
2 5 7
(2)
4 9 5
f
+
= = −
−
Equació de la tangent: (2) '(2)( 2)y f f x− = − ⇔
7 33
( 2)
5 25
y x+ = − −
b) Domini: { } { }2
9 0 3, 3Dom f x x= ∈ − ≠ = − −
Asímptotes verticals: si n’hi ha han d’estar en els punts en què el denominador val 0 :
3
( ' )
( )
(x
per l esquerra
lím f x
per la dreta→−
+∞
= 
−∞ 3
( )
( )
( ' )x
per la dreta
lím f x
per l esquerra→+
+∞
= 
−∞
Per tant hi ha dues asímptotes verticals d’equacions: 3x = − i 3x =
Asímptota horitzontal: 2
5 (1 5/ ) 1 5/
( ) 0
9 ( 9/ ) 9/x x x x
x x x x
lím f x lím lím lím
x x x x x x→± ∞ →± ∞ →± ∞ →± ∞
+ + +
= = = =
− − −
Per tant hi
ha una asímptota horitzontal (per la dreta i per l’esquerra) d’equació: 0y =
Com que n’hi ha d’horitzontal no pot haver-n’hi d’obliqües.
c) Busquem els possibles màxims i mínims:
( )
2
2
22
910 9
'( ) 0 0 10 9 0
19
x x
f x x x x
x
−+ +
= ⇔ − = ⇒ + + = ⇔ = 
−−
(punts singulars)
Es pot comprovar que:
Si 9x < − la derivada és negativa, per tant ( )f x és decreixent en ( , 9)−∞ −
Si 9 1x− < < − (excepte 3x = − ) la derivada és positiva, per tant ( )f x és creixent en
( 9, 3)− − i ( 3, 1)− −
Si 1x > − (excepte 3x = ) la derivada és negativa, per tant ( )f x és decreixent en ( 1, 3)− i
(3, )+ ∞
Es dedueix que ( )f x té un mínim relatiu en 9x = − i un màxim relatiu en 1x = −
–1 3– 9 – 3

11. 11
Observeu que el mínim és molt a
prop de l’eix d’abscisses, ja que
( 9) 0,06f − =
15
a) Si la tangent en 0x = és horitzontal, la derivada en aquest punt serà 0 .
3 2
'( ) 4 3 2 '(0)f x x a x b x c f c= + + + ⇒ = , per tant ha de ser 0c =
b) Si hi ha un extrem relatiu en 2x = − vol dir que '( 2) 0f − = , és a dir:
3 2
4( 2) 3 ( 2) 2 ( 2) 0 12 4 32a b a b− + − + − = ⇒ − = (1)
Si la gràfica talla l’eix d’abscisses en 1x = vol dir que (1) 0f = , és a dir: 8a b+ = − (2)
Resolem el sistema format per les equacions (1) i (2):
12 4 32
8
a b
a b
− =
⇔
+ = −
0
8
a
b
=

= −
c) Com a conseqüència dels resultats anteriors es dedueix que 4 2
( ) 8 7f x x x= − +
3
'( ) 4 16f x x x= − Busquem els possibles màxims i mínims:
3 2
0
'( ) 0 4 16 0 4 ( 4) 0 2
2
f x x x x x x


= ⇔ − = ⇔ − = ⇔ = −


(punts singulars)
2
''( ) 12 16f x x= − ; ''(0) 16 0f = − < , per tant hi ha un màxim relatiu en 0x =
2
''( 2) 12( 2) 16 32 0f − = − − = > , per tant hi ha un mínim relatiu en 2x = −
2
''(2) 12(2) 16 32 0f = − = > , per tant hi ha un mínim relatiu en 2x =
-3 3
-1-9

12. 12
Es dedueix que ( )f x és
decreixent en ( , 2)−∞ − i
en (0, 2) i és creixent en
( 2, 0)− i en (2, )+∞
(També es pot deduir
directament a partir del
signe de la derivada)
16
a) Domini: Com que la funció és la composició d’una exponencial i una polinòmica, i totes
dues tenen per domini , es dedueix que Dom f =
Interseccions amb els eixos: 0
(0) 1f e= = → (0, 1) (amb l’eix d’ordenades)
Com que una funció exponencial sempre és positiva, no hi ha intersecció amb l’eix
d’abscisses.
b) ( )
2
2
'( ) 2 2x x
f x e x− +
= − + Busquem els punts en què la derivada s’anul·la:
'( ) 0 2 2 0 1f x x x= ⇔ − + = ⇔ = (punt singular)
És clar que si 1x < la derivada és positiva i si 1x > la derivada és negativa, per tant la
funció és creixent en ( , 1)−∞ i decreixent en (1, )+∞ Es dedueix que té un màxim relatiu
en 1x =
D’asímptotes verticals no en té ja que la funció és contínua en tot el seu domini.
2
2
0x x
x
lím e e− + −∞
→+∞
 = =  , per tant té una asímptota horitzontal per la dreta d’equació:
0y =
2
2
0x x
x
lím e e− + −∞
→− ∞
 = =  , per tant l’asímptota anterior també ho és per l’esquerra.
Com que hi ha asímptotes horitzontals no n’hi pot haver d’obliqües.
(-2 , -9) (2 , 9)
(0 , 7)

13. 13
d) Noteu que, en
tractar-se d’una
exponencial, la funció és
positiva en tot el domini.
17
a) '( ) ( ) ( )x x x
f x e ax b ae e ax b a= + + = + + . Si la funció té un extrem en ( )3
3, e vol dir dues
coses:
3 3 3
3
3 1(3) (3 )
4 0'(3) 0 (4 ) 0
a bf e e a b e
a bf e a b
+ = = + = 
⇔ ⇔ ⇔  
+ == + =  
1
4
a
b
= −

=
b) ( ) ( 4)x
f x e x= − +
'( ) ( 3)x
f x e x= − +
''( ) ( 3) ( 2)x x x
f x e x e e x= − + − = − + 3
''(3) 0f e= − < , per tant es tracta d’un màxim
18
4 3 2 2 2 3 2 3 2
'( ) 30 60 30 30 ( 1) ; ''( ) 120 180 60 ; '''( ) 360 360 60f x x x x x x f x x x x f x x x= − + = − = − + = − +
Els pòssibles màxims i mínims han de trobar-se entre els punts que anul·len la derivada:
2 2 0
'( ) 0 30 ( 1) 0
1
f x x x x

= ⇔ − = ⇔ = 

Noteu que '( ) 0f x > per a qualsevol valor de x , per tant, la funció és creixent en tot el seu
domini i no té extrems. En els punts 0x = i 1x = la segona derivada també s’anul·la però la
tercera no, per tant són punts d’inflexió.
(1, 2.72)

14. 14
19
La funció étà definida i és contínua en { }3−
2 2 3 2 3 3 2 2
4 3 3 3
3 ( 3) 2( 3) 3 ( 3) 2 9 ( 9)
'( )
( 3) ( 3) ( 3) ( 3)
x x x x x x x x x x x
f x
x x x x
− − − − − − −
= = = =
− − − −
Evidentment la derivada s’anul·la per a 0x = i 9x = (punts singulars, possibles màxims o
mínims).
Observeu que el numerador serà negatiu si 9x < i positiu si 9x > , i el denominador serà
negatiu si 3x < i positiu si 3x > (perquè és una potència imparella). Es dedueix:
Si 3x < serà '( ) 0f x > , per tant la funció serà creixent en ( , 3)−∞
Si 3 9x< < serà '( ) 0f x < , per tant la funció serà decreixent en (3, 9)
Si 9x > serà '( ) 0f x > , per tant la funció serà creixent en (9, )+∞
Es dedueix que hi ha un mínim relatiu en 9x = (En 3x = hi ha canvi de creixement, però no hi
ha extrem ja que la funció no hi està definida.)
20
a) En el punt 1x = la funció és discontínua. Si el numerador no s’anul·la en 1x = , la
discontinuïtat serà infinita. Si el numerador s’anul·la en 1x = la discontinuïtat pot ser evitable.
Perquè el numerador s’anul·li en 1x = ha de ser 2 0 2m m− = ⇔ =
Si 2m = :
1 1 1
2 2 2 2( 1)
2
1 1 1x x x
mx x x
lím lím lím
x x x→ → →
− − −
= = =
− − −
(disc. evitable)
Si 2m ≠ :
1
1 2 1 22 2
1 0 1 2 1 2x
si x i m o bé si x i mmx m
lím
x si x i m o bé si x i m
+ −
+ +→
+∞ → > → <− − 
= =  − −∞ → < → >  
b) 2 2
( 1) ( 2) 2
'( )
( 1) ( 1)
m x mx m
f x
x x
− − − −
= =
− −
Perquè la derivada sigui positiva per a tot valor de x , el
numerador de la derivada ha de ser positiu: 2 0m− > ⇔ 2m <

15. 15
21
{ } { }1 0 1Dom f x x= ∈ − ≠ = −
Asímptotes verticals:
2
1 1
14 1 2
( )
1 0 1x x
si xx x
lím f x lím
x si x
−
+→ →
 +∞ →− + − 
= = =  − − ∞ →  
, per tant hi ha una
asímptota vertical d’equació: 1x =
Asímptotes horitzontals:
2
4 1 4 1/
( )
1 1 1/x x x
x x x x
lím f x lím lím
x x→±∞ →±∞ →±∞
− + − +
= = = ±∞
− −
Per tant no hi ha
asímptota horitzontal per cap costat.
Asímptotes obliqües: y mx n= +
2 2
2
( ) 4 1 1 4/ 1/
1
1 1/x x x
f x x x x x
lím lím lím m
x x x x→±∞ →±∞ →±∞
− + − +
= = = =
− −
(pendent de l’asímptota obliqua)
[ ]
2
4 1 3 1
( ) 3
1 1x x x
x x x
lím f x mx lím x lím n
x x→±∞ →±∞ →±∞
− + − +
− = − = = − =
− −
(ordenada a l’origen de l’asímptota)
Per tant hi ha asímptota obliqua (per l’esquerra i per la dreta) d’equació: 3y x= −