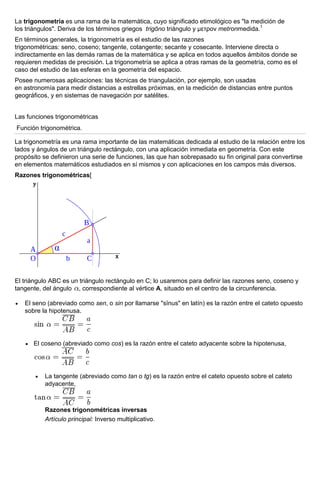
1. La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de
los triángulos". Deriva de los términos griegos trigōno triángulo y μετρον metronmedida.1
En términos generales, la trigonometría es el estudio de las razones
trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o
indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se
requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el
caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas
en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos
geográficos, y en sistemas de navegación por satélites.
Las funciones trigonométricas
Función trigonométrica.
La trigonometría es una rama importante de las matemáticas dedicada al estudio de la relación entre los
lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría. Con este
propósito se definieron una serie de funciones, las que han sobrepasado su fin original para convertirse
en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.
Razones trigonométricas[
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y
tangente, del ángulo , correspondiente al vértice A, situado en el centro de la circunferencia.
El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto
sobre la hipotenusa.
El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto
adyacente,
Razones trigonométricas inversas
Artículo principal: Inverso multiplicativo.

2. Triángulo ABC proporcional con un ángulo inscrito en una circunferencia de centro A y
radio 1
La Cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su
inverso multiplicativo:
En el esquema su representación geométrica es:
La Secante: (abreviado como sec) es la razón inversa de coseno, o también su
inverso multiplicativo:
En el esquema su representación geométrica es:
La Cotangente: (abreviado como cot o cta) es la razón inversa de la
tangente, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
Normalmente se emplean las relaciones trigonométricas seno, coseno
y tangente, y salvo que haya un interés específico en hablar de ellos o
las expresiones matemáticas se simplifiquen mucho, los términos
cosecante, secante y cotangente no suelen utilizarse.
(M-6) El Teorema de Pitágoras
Pitágoras de Samos fue un filósofo griego que vivió alrededor del año 530
a.C., residiendo la mayor parte de su vida en la colonia griega de Crotona,
en el sur de Italia. De acuerdo con la tradición fue el primero en probar la
afirmación (teorema) que hoy lleva su nombre:
Si un triángulo tiene lados de longitud (a,b,c), con los lados (a,b)
formando un ángulo de 90 grados ("ángulo recto"), tenemos que
a2
+ b2
= c2
Un ángulo recto se puede definir como el ángulo formado cuando dos
líneas rectas se cruzan de tal forma que los cuatro ángulos que forman

3. son iguales. El teorema también se puede definir de otra forma: si las
longitudes de los tres lados (a,b,c) de un triángulo satisfacen la relación
anterior, el ángulo entre los lados a y b debe ser de 90 grados.
Por ejemplo, un triángulo con los lados a = 3, b = 4, c = 5 (pulgadas, pies,
metros,... lo que sea) es rectángulo porque
a2
+ b2
= 32
+ 42
= 9 + 16 = 25 = c2
Los maestros de obras del antiguo Egipto pudieron conocer el triángulo
(3,4,5) y usarlo (mediante cañas o cuerdas calibradas) para construir
ángulos rectos; aún hoy en día los albañiles usan tableros con clavos con
esas longitudes que les ayudan a alinear una esquina.
Existen muchas pruebas, y las más fáciles son probablemente las que
están basadas en el álgebra, usando las igualdades elementales presentadas
en la sección precedente, a saber
(a + b)2
= a2
+ 2ab + b2
(recuerde que 2ab significa 2 veces a veces b). Por
ejemplo
152
= (10 + 5)2
= 102
+ (2)(10)(5) + 52
= 100 + 100 + 25 = 225
y
(a - b) 2
= a2
- 2ab + b2
Por ejemplo:
52
= (10 - 5)2
= 102
- (2)(10)(5) + 52
= 100 - 100 + 25 = 25
También es necesario conocer algunas áreas simples: el área de un
rectángulo es (longitud) por (altura), de tal forma que el área del
presentado arriba es ab. Una diagonal lo divide en dos triángulos
rectángulos siendo los lados cortos a y b, y el área de ese triángulo es,
por consiguiente, (1/2) ab.
Vea el cuadrado de la izquierda construido
por cuatro triángulos (a,b,c). la longitud de
cada lado es (a+b) y, por lo tanto, el
cuadrado tiene un área de (a+b)2
.
No obstante, el cuadrado se puede a su vez
dividir en cuatro triángulos (a,b,c) más un
cuadrado de lado c en el centro (en rigor,
también debemos de probar que es un
cuadrado, pero nos saltaremos esto). El área de cada triángulo, como se
mostró anteriormente, es (1/2)ab, y el área del cuadrado es c2
. Como el
cuadrado grande es igual a la suma de todas sus partes
(a + b) 2
= (4)(1/2)(a)(b) + c2

4. Usando la igualdad para (a + b)2
y multiplicando (4)(1/2) = 2
a2
+ 2ab + b2
= 2ab + c2
Reste 2ab de ambos lados y obtendrá
a2
+ b2
= c2
Se puede mostrar el mismo resultado usando
un cuadrado diferente, de área c2
. Como
muestra el dibujo de la derecha, esa área puede
dividirse en cuatro triángulos como los
anteriores, más un pequeño cuadrado de lado
(a-b). Obtenemos
c2
= (4)(1/2)(a)(b) + (a-b) 2
= 2ab + (a2
- 2ab + b2
)
= a2
+ b2
Q.E.D.
Q.E.D. simboliza "quod erat demonstrandum," en latín "lo que queda
demostrado," que en los libros de geometría, tradicionalmente, marcaban
el final de una demostración. La importancia del trabajo de Pitágoras y de
los siguientes maestros de geometría griegos, especialmente Euclides, no
fue solo lo que probaron, sino elmétodo que desarrollaron: comenzar
desde algunas afirmaciones básicas ("axiomas") y deducir mediante la
lógica sus consecuencias más complicadas ("teoremas"). Los matemáticos
aún siguen ese modelo.
Teorema del Seno
En el triángulo ABC, este es inscrito en una circunferencia* de centro O. El diámetro* trazado por
A, corta a la circunferencia en el punto C'. El ángulo ABC' esta recto en el punto B, por que se
trata de un ángulo inscrito*, que abarca un arco 180°.
En él se cumple que:
Sen C' = AB = c = c .
AC' diametro 2Radio

5. El ángulo C y el ángulo C' son iguales por ser ángulos inscritos, o sea el arco AB es:
Sen C = c/2R o sea,
2R = c .
Sen C
Lo mismo ocurre con los otros lados, o sea podemos deducir que:
2R= b . Y 2R= a .
Sen B Sen A
A partir de esta comprobación, podemos deducir como todos los enunciados empiezan en “2R”,
que:
2R= b . = a . = c .
Sen B Sen A Sen C
Glosario
Circunferencia: es el conjunto de puntos cuya distancia a otro punto llamado centro es siempre
la misma. Los puntos de la circunferencia y los que se encuentran dentro de ella forman una
superficie llamada círculo.
Diámetro: Un diámetro de un círculo es una recta cualquiera que pasa por el centro y que acaba
en ambas direcciones en la circunferencia del círculo; esta línea recta también divide el círculo
en dos partes iguales.
Radio: Un segmento lineal que une el centro del círculo con cualquier punto de la circunferencia
Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones
trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y
las operaciones aritméticas involucradas).
Notación: se define sin2
α como (sin α)2
. Lo mismo se aplica a las demás funciones trigonométricas.
FISICA
ENERGÍA (E)
La energía es una aplicación del trabajo y la potencia, ya que entre estas magnitudes un cuerpo puede
ser movido o ubicado con distintos valores, lo que hace que haya 3 tipos de energía:
Energía Cinética (Ec) Es el trabajo efectuado sobre un cuerpo de masa m; para acelerar un cuerpo
desde una velocidad inicial hasta una velocidad final, dependiendo de la masa del cuerpo a movilizar
La fórmula de la energía cinética es
Ec – energía cinética

6. Ec = m . V 2
m – masa del cuerpo
2 V – velocidad del cuerpo
Energía Potencial (Ep) Todo cuerpo de masa m que se encuentre a una altura h con respecto a un nivel
dado posee energía potencial gravitacional.
La fórmula de la energía cinética es
Ep – energía potencial
Ep = m . g .h m – masa del cuerpo
h – altura
Energía Potencial elástica (Epe) Todo cuerpo de masa m que se encuentre sometido a la fuerza elástica
de un resorte, el sistema masa-resorte posee energía potencial elástica
La fórmula de la energía cinética es
Epe – energía potencial elástica
Epe = K . X2
k – constante elástica
2 X – estiramiento o contracción del
resorte
Ejemplos
Calcular la energía cinética y potencial de un cuerpo de 14kg cuando se mueve con una velocidad de
15 m/sg y cuando se encuentra a una altura de 11 m de altura.
Datos
m = 10kg
v = 15 m/sg
h = 11m
Ec - ? Ec = m . V 2
/ 2 entonces Ec = 10kg . (15 m/sg)2
/ 2 es decir Ec = 10kg . 225 m2
/sg2
/ 2 o sea
Ec =2250kg m2
/sg2
Ec = 1125Jul 2
Ep - ? Ep = m . g .h entonces Ep = 10kg . 10m/sg2
. 11m es decir Ep = 1100kg m2
/sg2
o sea
Ep = 1100Jul
Calcular la energía potencial elástica de un cuerpo suspendido de un resorte cuya constante elástica es
de 24Nw/m y lo estira 0,5m
Datos
K = 24Nw/m
X = 0,5m

7. Epe - ? Epe = K . X2
/ 2 entonces Epe = 24Nw/m . (0,5m)2
es decir Epe = 24Nw/m . 0,25m2
o sea
Epe = 6Jjul
FUERZAS MECÁNICAS
Identificación de variables: fr – fuerza de rozamiento, Fe –fuerza elástica, Fc – fuerza centrípeta
Ej. Calcular el rozamiento de un cuerpo si los coeficientes cinético y estático son 0,5 y 0,8
respectivamente y la normal es de 450Nw
Datos
fr -? uc = 0,5 ue = 0,8 N =
450Nw
fr = uc . N fr = ue . N
Reemplazo datos: fr = uc . N entonces fr = 0,5 . 450Nw o sea fr = 225Nw
Reemplazo datos: fr = ue . N entonces fr = 0,8 . 450Nw o sea fr = 360Nw
Ej. Calcular la fuerza elástica de un resorte de constante 0,87Nw/cm si sostiene suspendida una masa
que lo estira 2m
Datos
Fe -? x = 2m = 200cm k = 0,87Nw/cm
Fe = -k . x
Reemplazo datos: Fe = -k . x entonces Fe = -0,87Nw/cm . 200cm o sea Fe = -174Nw
Ej. Calcular la fuerza centrípeta de un cuerpo de masa 20kg si su velocidad tangencial es de 12m/sg y
un radio de 3m
Datos
Fc -? vt = 12m/sg r = 3m
Fc = m . (vt)2
/ r
Reemplazo datos: Fc = (vt)2
/ r entonces Fc = 20kg . (12m/sg)2
/ 3m o sea Fc = 20kg .144m2
/sg2
/ 3m
es decir
Fc = 2880 kg . m/sg2
/ 3 por tanto Fc = 960Nw
Desarrollar los siguientes ejercicios

8. Posición Sitio se encuentra un cuerpo. Se acostumbra reconocer este lugar mediante una letra
mayúscula.
Ej. Escribe la posición de cada cuerpo.
-3 -2 -1 0 1 2 3 4 5 6____ X
F A B D C E
A está en -1
B está en 0
C está en 4
D está en 2
E está en 5
F está en -3
EJERCICIOS DE POSICIÓN
Escribe la posición de cada
cuerpo.
a)
-3 -2 -1 0 1 2
3__4 5 6 7 8_ X
F A B D C
G E H
b)
-3 -2 -1 0 1 2
3__________ X
A B C D
c)
-3 -2 -1 0 1 2
3__________ X
A B C D

9. EJERCICIOS DE ANALISIS GRAFICO
Calculemos posiciones y desplazamientos según los siguientes dibujos.
X (m) X (m)
C B
3 3
B D C
2 2 A
A E E
1 1
1 2 3 4 5 6 7 t (sg) 1 2 3 4 5 6 7
t (sg)
X (m)
3
A E
2 B D F
1 C
1 2 3 4 5 6 7 8 t (sg)

10. .
Velocidad. Es el distancia sobre el tiempo
Movimiento Rectilíneo Uniforme (M.R.U.). Se presenta cuando un cuerpo recorre
distancias iguales en tiempos iguales
Fórmula fundamental. V = x / t
Identificación de variables relacionadas: v – velocidad, x – distancia, t - tiempo
Unidades de velocidad: m / sg; km / h
EJEMPLOS DE VELOCIDAD
Calcular la velocidad de un auto que recorre 480km en 8 horas.
Como v = x / t entonces v = 480km / 8 h v = 60km/h
EJERCICIOS DE VELOCIDAD
MOVIMIENTO UNIFORME ACELERADO
Conceptos.
Aceleración (a). Es la velocidad entre el tiempo.
Movimiento Uniformemente Acelerado (MUA). Se presenta cuando un cuerpo
cambia velocidades iguales en tiempos iguales
Fórmulas.
a = v / t 1 vf = vi + a . t 2 x = vi . t + a . t2
/ 2 3
2 . a . x = vf
2 –
vi
2
4
Identificación de variables relacionadas: a–aceleración; v–velocidad; t–tiempo;
vi, vf -velocidades inicial y final; x -posición

11. EJEMPLOS DE LAS FORMULAS 1 Y 2
Calcular la aceleración de un auto si aumenta su velocidad a razón de 10m/sg
durante 20 segundos.
Solución. Como a = v / t 1 entonces a = 10m/sg / 20sg por tanto a =
0,5m/sg2
Calcular la velocidad final del auto anterior si su velocidad inicial fue de 3m/sg.
Solución. Como vf = vi + a . t 2 entonces vf = 3m/sg + (0,5m/sg2
. 20sg) por
tanto vf = 3m/sg + 10m/sg o sea vf = 13m/sg
EJEMPLOS DE LAS FORMULAS 3 Y 4
Calcular la distancia que recorrió el auto anterior.
Solución. Como x = vi . t + a . t2
/ 2 3 entonces x = (3m/sg . 20 sg) + 0,5m/sg2
.
(20sg)2
/2
por tanto x = 60m + 0,5m/sg2
. 400sg2
/2
entonces x = 60m + 100m o sea x =
160m
Calcular la distancia recorrida por un auto que acelera 1m/sg2
al cambiar su
velocidad de 2m/sg a 6 m/sg.
Solución. Como 2 . a . x = vf
2 –
vi
2
4 entonces 2 . 1m/sg2
. x = (6 m/sg)2
–
(2m/sg)2
o sea 2m/sg2
. x = 36m2
/sg2
- 4 m2
/sg2
Por tanto 2m/sg2
. x = 32 m2
/sg2
entonces x = 16m

12. MOVIMIENTO SEMIPARABÓLICO Y PARABÓLICO
Instrucciones: Desarrollar ordenadamente los ejercicios de acuerdo a los ejemplos
resueltos y conceptos. No olvides pegar esta guía en tu cuaderno
Movimiento semiparabólico. Si un objeto esférico es lanzado desde el filo de una
superficie alta entonces el cuerpo se somete a dos movimientos simultáneos ( X,
Y), cada uno se realiza independientemente.
Movimiento parabólico. Cuando un cuerpo se lanza con un ángulo de inclinación
cerca de la tierra.
-=
y
x
Movimiento semiparabólico
Fórmulas del movimiento semiparabólico.
alcance horizontal altura
x = vi . t y = g . t2
/ 2
EJEMPLOS RESUELTOS

13. Del movimiento semiparabólico:
Calcular posición y altura de un paracaidista que se lanzó desde un avión hace
20sg con una velocidad inicial de 167m/sg
Datos
t = 20sg
vi = 167 m/sg
Posición x = vi . t Reemplazo datos x = 167m/sg . 20sg entonces x =
334m
Altura y = g . t2
/ 2 Reemplazo datos y = 10m/sg2
. (20sg)2
/ 2 entonces
y = 10m/sg2
. 400sg2
/ 2 por tanto y = 400m / 2 o sea y = 200m
MOVIMIENTO PARABÓLICO
Ymax tv
Xmax
Movimiento parabólico
Fórmulas del movimiento parabólico.

14. Alcance máximo Altura máxima
Tiempo de vuelo
Xmax = vi
2
. sen2 ymáx = Vi
2
. sen2
tv = 2Vi . sen
g g g
Identificación de variables relacionadas: x - posición t-tiempo vi-velocidad inicial
g-gravedad (10m/sg2
) ángulo de tiro
EJEMPLO RESUELTO
Calcular alcance máximo, la altura máxima y el tiempo de vuelo de un balón que
fue lanzado con una velocidad de 8 m/sg y un ángulo de tiro de 30º
Datos
Xmax - ? Xmax = vi
2
. sen2 ymáx = Vi
2
. cos2
tv = 2Vi . sen
Ymax – ? g g
g
tv - ?
Vi = 8 m/sg
30º
Reemplazo datos
Xmax = (8 m/sg)2
. sen 2 . 30º Xmax = 64 m2
/sg2
. sen 60º : Xmax = 6,4 m . 0,8 :
Xmax = 5,12m
10m/sg2
10m/sg2
Ymax = (8 m/sg)2
. cos2
. 30º Ymax = 64 m2
/sg2
. (0,5)2
: Ymax = 6,4 m . 0,25
: Ymax = 1,6m

15. 10m/sg2
10m/sg2
tv = 2 . 8 m/sg . sen 30º : tv = 16 m/sg . 0,5 : tv = 1,6 sg . 0,5
: tv = 0,8sg
10 m/sg2
10 m/sg2
EJERCICIOS MOVIMIENTO PARABÓLICO
MOVIMIENTO CIRCULAR UNIFORME (M.C.U.)
Conceptos
Frecuencia es el tiempo que tarda un cuerpo en realizar una oscilación. Se mide
en Hertz y su abreviatura Hz
Periodo es el número de oscilaciones que realiza un cuerpo en la unidad del
tiempo
Velocidad tangencial Es la rapidez tangente a la trayectoria con la que se mueve
un cuerpo circularmente.
Velocidad angular Es la rapidez con la que barre un ángulo un cuerpo que se
mueve circularmente
Fórmulas del movimiento circular uniforme.
Periodo (T) Frecuencia (f) velocidad tangencial
(vt) velocidad angular aceleración centrípeta (ac)
T = t / # vueltas 1 f = # vueltas / t 2 vt = 2 r / T 3 w = 2 / T
4 ac = ( vt )2
/ r 5
Identificación de variables relacionadas:

16. T-periodo; f- frecuencia; t-tiempo; w-velocidad angular; vt-velocidad tangencial;
=3,14; aceleración centrípeta (ac); r-radio
Ejemplo resuelto
Calcular la frecuencia, periodo, velocidad angular, velocidad tangencial y
aceleración centrípeta de un motor que en 10segundos realiza 50 vueltas, si el
radio del M.C.U. es de 30 cm
Datos
t = 10 sg
# vueltas = 50
r = 30 cm
T - ? T = t / # vueltas entonces T = 10 sg / 50 o sea T = 0,2 sg
f - ? f = # vueltas / t entonces f = 50 / 10 sg o sea f = 5 Hertz ó
f = 5 Hz
vt- ? vt = 2 r / T entonces vt = 2 3,14 . 30 cm / 0,2 sg es decir vt = 6,
28 . 30 cm / 0,2 sg entonces
vt = 188,84 cm / 0,2 sg o sea vt = 942 cm / sg
w - ? w = 2 / T entonces w = 2 . 3,14 / 0,2 sg o sea w = 6,28 / 0,2
sg w = 31,4 / sg
ac - ? ac = ( vt )2
entonces ac = (942 cm / sg )2
es decir ac = 887364
cm2
/sg2
o sea ac = 29578,8 cm/sg2
30 cm 30 cm 30 cm