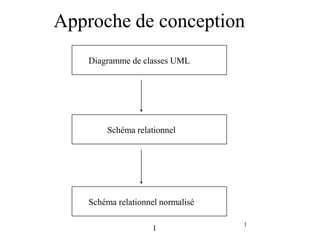
1.
1
1
Approche de conception
Diagramme de classes UML
Schéma relationnel
Schéma relationnel normalisé

2.
2
Le modèle relationnel
• Définitions :
– Relation, schéma relationnel, clé, contrainte d’intégrité
• Processus de normalisation
– Dépendance fonctionnelle simple, multivaluées
– 1NF, 2NF, 3NF, BCNF, 4NF

3.
3
• 1970 par Codd (IBM San José)
• 1ère réalisations (System-R, Ingres), vers 1976
• Les premiers systèmes commerciaux, au début des années 80
• Le modèle relationnel est simple, facile à appréhender,
même pour un non spécialiste.
• Solides bases théoriques: définir de façon formelle les
langages de manipulation associés
• Les relations qui peuvent être manipulées par des opérateurs
(algèbre relationnelle)
• Langage standardisé : SQL

4.
4
Modèle relationnel
• les données sont organisées sous forme de tables à
deux dimensions, encore appelées relations, dont
les lignes sont appelées « tuple » ou « n-uplet »
– Une ligne représente un objet
– Une colonne un attribut
• les données sont manipulées par des opérateurs de
l’algèbre relationnelle
• l’état cohérent de la base est défini par un
ensemble de contraintes d’intégrité

5.
5
Définitions (1)
• Un attribut est un nom décrivant une information stockée dans une
base. Exemples d’attribut : l’âge d’une personne, son nom, le numéro
de sécurité sociale
• Le domaine d’un attribut est l’ensemble, fini ou infini, de ses valeurs
possibles. Exemple : l’attribut numéro de sécurité sociale a pour
domaine l’ensemble des combinaisons de quinze chiffres; l’attribut
nom a pour domaine l’ensemble des chaînes de caractères. Un attribut
a une valeur atomique
• Une relation est un sous-ensemble du produit cartésien de n domaines
d’attributs (n>0). Une relation est représentée sous la forme d’une table
à deux dimensions dans laquelle les n attributs correspondent aux titres
des n colonnes.

6.
6
Définitions (2)
• Un schéma de relation précise le nom de la relation ainsi
que la liste ordonnée des attributs avec leurs domaines
• Relation Etudiant: Etudiant(no,nom,prenom,age)
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr
attribut
n-uplet
ou
tuple
no
12
1
4
8
nom
Ernest
Barnabé
Gertrude
Gaetan
prenom
Michèle
Pascal
François
Alain
age
20
23
22
22
Domaine de l’attribut
age: entier
15 Dupond Loïc 19

7.
7
Définitions (3)
• Le degré d’une relation est son nombre d’attributs.
• Une occurrence, ou n-uplet ou tuple, est un élément de
l’ensemble figuré par la relation. Autrement dit, une
occurrence est une ligne de la table qui représente la
relation.
• La cardinalité d’une relation est son nombre
d’occurrences.
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

8.
8
Définitions (4)
• Une clé candidate d’une relation est un ensemble minimal d’attributs
de la relation dont les valeurs identifient à coup sûr une occurrence. La
valeur d’une clé candidate est donc distincte pour tous les tuples de la
relation.
– Règle : toute relation a au moins une clé candidate et peut en avoir plusieurs. Ainsi,
il ne peut jamais y avoir deux tuples identiques au sein d’une relation.
• Les clés candidates d’une relation n’ont pas forcément le même
nombre d’attributs. Une clé candidate peut être formée d’un attribut
arbitraire qui n’a d’autre objectif que de servir de clé.
• La clé primaire d’une relation est une de ses clés candidates. Pour
signaler la clé primaire, ses attributs sont généralement soulignés.
• Une clé étrangère dans une relation est formée d’un ou plusieurs
attributs qui constituent une clé candidate dans une autre relation.

9.
9
Définitions (5)
• Un schéma relationnel est constitué par l’ensemble des
schémas de relations
• On parle aussi d’intension de la base de données
• Une base de données relationnelle est constituée par
l’ensemble des n-uplets des différentes relations du schéma
relationnel.
• On parle aussi d’extension de la base de données

10.
10
Définitions (6)
• Contrainte d’intégrité : propriété qui doit être vérifiée par
les données d’une table
– Contrainte statique : tout au long de la vie de la base
– Contrainte dynamique : lors du changement d’état (modification des
données), entre plusieurs (deux) états valides de la base.
• Exemples :
– La valeur d’un attribut ne peut pas être nulle
– heure>8h00 et heure<20h00
– un salaire ne peut pas baisser

11.
11
Bases de Données, 3ème année
• Contrainte de référence : lorsqu’une relation contient des
clés étrangères, les n-uplets correspondant à ces clés
doivent exister dans la relation référencée
• Soient Employe(no_emp, nom_emp, adresse_emp, role,
no_dept) et Departement(no_dept, nom_dep)
- Les employés ne peuvent être affectés qu’à des
départements qui existent
- On ne peut supprimer un département dans le quel il y a
un employé
Définitions (7)

12.
12
Bases de Données, 3ème année
Projection Relation  Table
• schéma  structure des enregistrements,
• n-uplet  enregistrement (ligne)
• attribut  champ (colonne)
• clé primaire  index

13.
13
Normalisation

14.
14
Normalisation : objectif
• l’objectif de la normalisation est d’assurer
qu’un schéma relationnel a les bonnes
propriétés
– Minimiser les redondances pour supprimer
• Les anomalies de modification
• Les anomalies d’insertion
• Les anomalies de suppression

15.
15
Limite des systèmes à une table
• Exemple: tables des propriétaires de voitures
PROPRIO Noinsee Nom NoImmat Type Puissance
188… MARTIN AB123CD Clio 192 6
267… SIMON BD345EF Clio 192 6
188… MARTIN CD354AB Peu. 208 23 6
278… DURAND AB456OP Espace 777 10
190… SCHMITT EA678AA C3 821 5

16.
16
Limite des systèmes à une table
Anomalie de mise à jour
Noinsee Nom NoImmat. Type Puissance
188… MARTIN AB123CD Clio 192 6
267… SIMON BD345EF Clio 192 6
188… MARTIN CD354AB Peu208 23 6
278… DURAND AB456OP Espace 777 10
190… SCHMITT EA678AA C3 821 5
• S’il y a modification de la puissance d’un type de
voiture, il y a autant d’opérations que de voitures
de ce type

17.
17
Limite des systèmes à une table
Anomalie d’insertion
• Exemple: on ne peut pas stocker les informations
sur un type de voiture qui n’est pas la propriété
d’une personne (ou alors table pleine de trous …)
Noinsee Nom NoImmat. Type Puissance
188… MARTIN AB123CD Clio 192 6
267… SIMON BD345EF Clio 192 6
188… MARTIN CD354AB Peu208 23 6
278… DURAND AB456OP Espace 777 10
190… SCHMITT EA678AA C3 821 5

18.
18
Limite des systèmes à une table
Anomalie de suppression
• Exemple: si on supprime la personne 158..., on
supprime complètement le type de voiture PEU208 23
Noinsee Nom NoImmat. Type Puissance
188… MARTIN AB123CD Clio 192 6
267… SIMON BD345EF Clio 192 6
188… MARTIN CD354AB Peu208 23 6
278… DURAND AB456OP Espace 777 10
190… SCHMITT EA678AA C3 821 5

19.
19
Meilleure solution
PROPRIO Noinsee Nom
188… MARTIN
267… SIMON
158… MARTIN
278… DURAND
190… SCHMITT
POSSEDE Noinsee Noimmat
188… AB123CD
267… BD345EF
158… CD354AB
278… AB456OP
190… EA678AA
VOITURE Noimmat Type
AB123CD Clio 192
BD345EF Clio 192
CD354AB Peu208 23
AB456OP Espace 777
EA678AA C3 821
TYPE Type Puissance
Clio 192 6
Peu208 23 6
Espace 777 10
C3 821 5

20.
20
Dépendance fonctionnelle (DF)
• Soit R(U) une relation avec U l'ensemble de ses attributs.
• Soit X, Y  U, i.e X et Y sont deux attributs ou ensemble
d'attributs de R. On dit qu'il existe une DF entre X et Y (ou que
X détermine Y ou encore que Y est déterminé par X), notée
X Y si et seulement si :
 tl et t2, deux tuples de R, si tl[X] = t2[X] alors tl[Y] = t2[Y]
Pour une DF X  Y, X est la source et Y la cible.
• A une valeur de X ne correspond qu’une valeur de Y
Exemple : noinsee  nom
• Dans une relation, tout attribut est en DF avec la clef primaire

21.
21
Propriété des DFs
Réflexivité Si Y  X alors X  Y (et donc X  X)
Augmentation Si X  Y et W  Z alors X, Z  Y, W
Transitivité Si X Y et Y  Z alors X  Z
Pseudo-transitivité Si X Y et Y, Z  W alors X, Z W
Union Si X  Y et X  Z alors X  Y, Z
Décomposition Si X  Y, Z alors X  Y et X  Z

22.
22
DF et clé candidate
• Soit R(U) une relation et X  U.
• X est une clef possible ou candidate si et
seulement si on a X  Y où Y = U - X (i.e.
le complémentaire de X dans U).
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

23.
23
DF élémentaire et clé minimale
• Soit R(U) une relation et X  U
On a une DF élémentaire entre X et Y, X Y de façon
élémentaire si et seulement si :  X'  X, X'  Y n'est pas
vérifiée.
• Soit X est une clef de R,
on dit que X est une clef minimale de R si et seulement si 
X'  X, X' n'est pas une clef de R
• Si  Y  (U-X), la DF X  Y est élémentaire
Ex : Noinsee  nom (élémentaire)
Noinsee, NoImmat  nom (non élémentaire)

24.
24
DF et normalisation
• Théorème de décomposition
Soit R(X,Y,Z) une relation où X, Y, Z sont
des ensembles d’attributs, et X Y,
alors la décomposition de R (X,Y) en
R1(X,Y) et R2 (X,Z) est sans perte
d’information
(pas de perte de données ni de DFs).

25.
25
Relation en 1NF
• Une relation est en première forme normale si tous
ses attributs sont atomiques
• Passage en 1NF :
– Supprimer les attributs composés en les remplaçant par
autant d’attributs que nécessaire
– (choisir une clé primaire)
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

26.
26
Relation en 2NF
• Une relation est en 2NF si :
– Elle est en 1NF
– Tout attribut n’appartenant pas à la clé primaire
est en DF élémentaire avec cette clé
• Passage en 2NF :
– Isoler la DF non élémentaire en créant une nouvelle
relation
– Eliminer l’attribut cible de la DF de la relation initiale
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

27.
27
Relation en 3NF
• Une relation est en 3NF si:
– Elle est en 2NF
– Elle ne contient pas de DF transitive entre
attributs non clé
• Passage en 3NF :
– Isoler la DF non directe en créant une nouvelle relation
– Eliminer l’attribut cible de DF de la relation initiale

28.
28
Exemple 1NF
Noinsee, NoImmat  Nom, Type, Puissance
Noinsee  Nom
NoImmat  Type, Puissance
Type  Puissance
PROPRIO Noinsee Nom NoImmat Type Puissance
188… MARTIN AB123CD Clio 192 6
267… SIMON BD345EF Clio 192 6
188… MARTIN CD354AB Peu. 208 23 6
278… DURAND AB456OP Espace 777 10
190… SCHMITT EA678AA C3 821 5

29.
29
Exemple 2NF
PROPRIO Noinsee Nom
188… MARTIN
267… SIMON
158… MARTIN
278… DURAND
190… SCHMITT
VOITURE Noimmat Type Puissance
AB123CD Clio 192 6
BD345EF Clio 192 6
CD354AB Peu208 23 6
AB456OP Espace 777 10
EA678AA C3 821 5
POSSEDE Noinsee Noimmat
188… AB123CD
267… BD345EF
158… CD354AB
278… AB456OP
190… EA678AA
Noinsee, NoImmat  Nom, Type, Puissance
Noinsee  Nom
NoImmat  Type, Puissance
Type  Puissance

30.
30
Exemple 3NF
PROPRIO Noinsee Nom
188… MARTIN
267… SIMON
158… MARTIN
278… DURAND
190… SCHMITT
POSSEDE Noinsee Noimmat
188… AB123CD
267… BD345EF
158… CD354AB
278… AB456OP
190… EA678AA
VOITURE Noimmat Type
AB123CD Clio 192
BD345EF Clio 192
CD354AB Peu208 23
AB456OP Espace 777
EA678AA C3 821
TYPE Type Puissance
Clio 192 6
Peu208 23 6
Espace 777 10
C3 821 5
Noinsee, NoImmat  Nom, Type, Puissance,
Noinsee  Nom, NoImmat  Type, Puissance, Type  Puissance

31.
31
Une relation en 3NF peut
comporter des redondances
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr
• Exemple :
R(VILLE, DEPARTEMENT, CODE POSTAL)
avec les DF :
VILLE, DEPARTEMENT  CODE POSTAL
CODE POSTAL  DEPARTEMENT
• Redondance: on répète le département pour toutes
les villes ayant le même code postal

32.
32
Relation en Boyce–Codd NF
• Une relation est en BCNF si les seules
dépendances sont celles dans lesquelles une clé
détermine un attribut (=> 3NF)
• Passage en BCNF :
– Décomposer la relation en s’appuyant sur la DF
problématique :
• Créer une nouvelle relation pour cette DF.
• Eliminer la cible de la DF problématique dans la
relation initiale; modifier la clé en fonction.

33.
33
Relation en Boyce–Codd NF
• R (VILLE, DEPARTEMENT, CODE POSTAL) n'est pas
en BCNF
• Elle peut être décomposée :
R1 (VILLE, CODE POSTAL)
R2 (DEPARTEMENT, CODE POSTAL)
en utilisant en CODE POSTAL  DEPARTEMENT
• Mais on a perdu la dépendance
VILLE, DEPARTEMENT  CODE POSTAL

34.
34
Une relation en BCNF peut
comporter des redondances
• La relation ETUDIANT est en BCNF mais
contient des redondances
ETUDIANT NoEtudiant Sport Langue
188… Ski Anglais
188… Tennis Polonais
188… Ski Polonais
188… Tennis Anglais
190… Natation Anglais
191 Natation Italien

35.
35
Une relation en BCNF peut
comporter des redondances
• La relation ETUDIANT est en BCNF mais
contient des redondances car le fait qu’un
étudiant fasse un sport est indépendant des
langues qu’il parle
• Pour caractériser cette configuration, on
utilise les dépendances multivaluées

36.
36
Dépendance multivaluée (DM)
• Soient:
– R(A1, A2, …, An)
– X sous-ensemble de {A1, A2, …, An}
– Y sous-ensemble de {A1, A2, …, An}
– Z = {A1, A2, …, An} - X - Y
• X ->> Y (X multi-détermine Y) si :
<x,y,z> et <x,y’,z’> dans R =>
<x,y’,z> et <x,y,z’> dans R
A chaque valeur de X est associée un ensemble de valeurs de
Y indépendamment de Z
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

37.
37
Décomposition en 4ème forme normale
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr
• Soit R(X,Y,Z) et X ->> Y et X ->> Z, alors R se
décompose en :
– R1 (X,Y) et R2 (X, Z)
– R1 et R2 sont en 4NF
• Dans ETUDIANT(NoEtudiant, Sport, Langue), on a
NoEtudiant ->> Sport et NoEtudiant ->> Langue, donc
ETUDIANT se décompose en :
– ETUDIANT1(NoEtudiant, Sport) et
ETUDIANT2(NoEtudiant, Langue)

38.
38
Et ce n’est pas fini …
• Dépendances jointives
– 5NF
– Une relation peut se décomposer en plus de 2
relations
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr

39.
39
FIN
Bases de Données, 3ème année Claude.Godart@esstin.uhp-nancy.fr