For math engineering 1

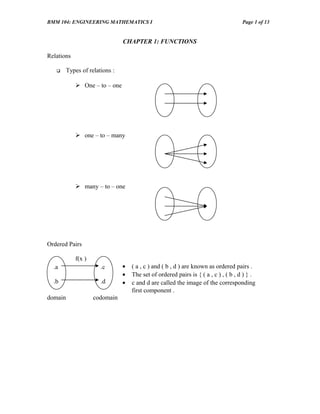
1. BMM 104: ENGINEERING MATHEMATICS I Page 1 of 13
CHAPTER 1: FUNCTIONS
Relations
 Types of relations :
 One – to – one
 one – to – many
 many – to – one
Ordered Pairs
f(x )
.a .c • ( a , c ) and ( b , d ) are known as ordered pairs .
• The set of ordered pairs is { ( a , c ) , ( b , d ) } .
.b .d • c and d are called the image of the corresponding
first component .
domain codomain

2. BMM 104: ENGINEERING MATHEMATICS I Page 2 of 13
Functions
 Definition Function
A relation in which every element in the domain has a unique
image in the codomain.
 Notation of functions :
A function f from x to y : f : x  y or y = f ( x )
f(x )
.a .c
.b .d
domain codomain
 Domain – set of input values for a function
Range – the corresponding output values
– is a subset of codomain
 Elements of domain { a , b }
Elements of codomain { c , d }
NOTE: Vertical line test can be used to determine whether a relation is a function or
not. A function f ( x ) can have only one value f ( x ) for each x in its domain, so no
vertical line can intersect the graph of a function more than once.
Example: Determine which of the following equations defines a function y in terms of x.
Sketch its graph.
(i) y + 2 x = 1 (ii) y = 3 x 2 (iii) x 2 + y 2 = 1
Domain and Range
The set D of all possible input values is called the domain of the function.
The set of all values of f ( x ) as x varies throughout D is called the range of the
function.
Example:

3. BMM 104: ENGINEERING MATHEMATICS I Page 3 of 13
Combining Functions
Sum, Differences, Products, and Quotients
Example: Attend lecture.
Composite Functions
If f and g are functions, the composite function f  g (“f composed with g”) is defined by
( f  g )( x ) = f ( g ( x )).
The domain of f  g consists of the numbers x in the domain of g for which g(x) lies in
the domain of f.
Example: Attend lecture.

4. BMM 104: ENGINEERING MATHEMATICS I Page 4 of 13
Inverse Functions
One-to-One Functions
A function f(x) is one-to-one if every two distinct values for x in the domain, x1 ≠ x 2 ,
correspond to two distinct values of the function, f ( x1 ) ≠ f ( x 2 ) .
Properties of a one-to-one function
(f −1
 f )( x ) = x and ( f  f )( y ) = y
−1
NOTE: A function y = f ( x ) is one-to-one if and only if its graph intersects each
horizontal line at most once.
Inverse Functions
Finding the Inverse of a Function
Step 1: Verify that f(x) is a one-to-one function.
Step 2: Let y = f(x).
Step 3: Interchange x and y.
Step 4: Solve for y.
Step 5: Let y = f −1 ( x ) .
Step 6: Note any domain restrictions on f −1 ( x ) .
NOTE:
−1
 Domain of f = Range of f
−1
 Range of f = Domain of f
Example:
1. Find the inverse of the function f ( x ) = 2 x − 3 .
2. Find the inverse of the function f ( x ) = x 3 + 2 .
3. Find the inverse of the function f ( x ) = x + 2 .
2
4. Find the inverse of the function f ( x ) = , x ≠ −3 .
x +3
Even Function, Odd Function

5. BMM 104: ENGINEERING MATHEMATICS I Page 5 of 13
A function y = f ( x ) is an
even function of x if f ( −x ) = f ( x ) ,
odd function of x if f ( −x ) = − f ( x ) ,
for every x in the function’s domain.
Even Function
(Symmetric about the y-axis)
Odd Function
(Symmetric about the origin)
Example: Attend lecture.
Exponential functions

6. BMM 104: ENGINEERING MATHEMATICS I Page 6 of 13
Function of the form
f ( x) = a x , a ≠ 1
where a is positive constant is the general exponential function with base a and x as
exponent.
The most commonly used exponential function, commonly called natural exponential
function is
y =ex or y = exp( x )
where the base e is the exponential constant whose value is e ≈ 2.718281828...
Rules for exponential functions
i. e x .e y = e x + y ~ Product Rule
ex
ii. y
= e x−y ~ Quotient Rule
e
iii. (e )
x y
( )
= e xy = e y
x
~ Power Rule
1 1
iv. x
= e − x or −x
= ex ~ Reciprocal Rule
e e
v. e0 = 1
Example:
Solve the following exponent equations.
(a) 2x
2
+3
= 16 (b) 2 x 3 x +1 = 108 (c) ( 2) x2
=
8x
4
Logarithmic Functions

7. BMM 104: ENGINEERING MATHEMATICS I Page 7 of 13
The logarithm function with base a, y = log a x , is the inverse of the base a exponential
function y = a x ( a > 0 , a ≠ 1) .
The function y = ln x is called the natural logarithm function, and y = log x is often
called the common logarithm function. For natural logarithm,
y = ln x ⇔ ey = x
Algebraic properties of the natural logarithm
For any numbers b > 0 and x > 0 , the natural logarithm satisfies the following rules:
1. Product Rule: ln bx = ln b + ln x
b
2. Quotient Rule: ln = ln b − ln x
x
3. Power Rule: ln x r = r ln x
1
4. Reciprocal Rule: ln = −ln x
x
Inverse Properties for a x and log a x
1. Base a: a log a x = x , log a a x = x , a > 0 , a ≠ 1, x > 0
2. Base e: e ln x = x , ln e = x ,
x
x >0
Change Base Formula
Every logarithmic function is a constant multiple of the natural logarithm.
ln x
log a x = ( a > 0 , a ≠ 1)
ln a
NOTE: log a 1 = 0 .
Example 1: Rewrite the following expression in terms of logarithm.
i. 32 = 2 5 ii. 1000 = 10 3
1
iii. 0.001 = 10 −3 iv. 3 = 92
Example 2:
i. Evaluate log 2 3 .

8. BMM 104: ENGINEERING MATHEMATICS I Page 8 of 13
1 2
ii. Simplify log 2 8 − log 2 .
3 7
 1
iii. Simplify log 2   + log 2 128
8

10 x 
iv. Expand ln 2 
 y 
 
Example 3: Solve the following equations:
1. 39 = e x 2. 10 x = 0.32
3. ln 2 x = 1.36 4. log ( 3 x − 6 ) = 0.76
5. log 3 ( 2 x + 1) − 2 log 3 ( x − 3 ) = 2
6. 6 3 x +2 = 200
Trigonometric Functions
Example: Attend lecture.
Hyperbolic Functions
Hyperbolic functions are formed by taking combinations of the two exponential functions
e x and e −x .
The six basic hyperbolic functions
e x − e −x
1. Hyperbolic sine of x: sinh x =
2
e x + e −x
2. Hyperbolic cosine of x: cosh x =
2
ex − e −x
3. Hyperbolic tangent of x: tanh x =
ex + e −x
ex + e −x
4. Hyperbolic cotangent of x: coth x = x
e − e −x
2
5. Hyperbolic secant of x: sec hx = x
e + e −x
2
6. Hyperbolic cosecant of x: cos echx = x
e − e −x
Shifting a Graph of a Function

9. BMM 104: ENGINEERING MATHEMATICS I Page 9 of 13

10. BMM 104: ENGINEERING MATHEMATICS I Page 10 of 13

11. BMM 104: ENGINEERING MATHEMATICS I Page 11 of 13
Example: Attend lecture.
PROBLET SET: CHAPTER 1
1. Let f ( x ) = x 2 − 3 x and find each of the following:
1  1
(a) f ( −3 ) (b) f ( 5 ) (c) f ( 0 ) (d) f   (e) f  − 
2  2
(f) f ( a ) (g) f ( 2 x ) (h) 2 f ( x ) (i) f ( x + 3) (j) f ( x ) + f ( 3 )
1 1
(k) f   (l)
x f(x)
1
2. Let g ( x ) = . Evaluate and simplify the difference quotient:
x
g( 4 + h ) − g( 4 )
,h ≠ 0
h
3. Find the domain and range of the function defined by each equation.
y = ( x − 1) + 2
3
(a) (e) y = 5x 2
3
(b) y = 7 −x (f) y=
x +1
x
(c) y = −x 2 + 4 x − 1 (g) y=
x +3
x −2
(d) y = 3x + 5 (h) y=
x +3
4. Find f  g and g  f .
(a) f ( x ) = x 2 ; g( x ) = x − 1 (e) f ( x ) = x + 1 ; g( x ) = x 4 − 1
x +1
(b) f ( x ) = x −3 ; g ( x ) = 2 x +3 (f) f ( x ) = 2 x 3 − 1; g ( x ) = 3
2
x x +3
(c) f(x)= ; g( x ) = (g) f(x)= x ; g( x ) = 4
x −2 x
1
(d) f ( x ) = x 3 ; g( x ) = (h) f ( x ) = 3 1 − x ; g ( x ) = 1 − x 3
x +1
3

12. BMM 104: ENGINEERING MATHEMATICS I Page 12 of 13
5. Find the inverse g of the given function f, and state the domain and range of g.
y = ( x + 1) ; x ≥ −1
2
(a). (e). y = x 2 − 4; x ≥ 0
(b). y = x 2 − 4 x + 4; x ≥ 2 (f). y = 4 − x 2 ;0 ≤ x ≤ 2
1
(c). y= (i). y = x 2 − 4 x; x ≥ 2
x
(d). y =− x (j). y = 4x − x2 ; x ≥ 2
6. Determine whether the following functions are odd, even or neither even nor odd.
3
(a). f ( x) = − 2x (f). f ( x ) =−−8t + −7t
x2
(b).
(1 − x ) 3 (g).
f ( x) = 3
f ( x) = 3 x 3 − 3 x
x
cos x − x sin x − ( cos x )
2
(c). f ( x) = 2 (h). f ( x) =
3−x cot x sec x
x2
(d). f ( x ) = 3 x 4 sin x (i). f ( x) = cos x + +5
1− x4
x + x2
3
−
1
 2
2
(e). f ( x ) =x 3  −x 3
1 
 (j). f ( x) = tan x +
  sin x
ANSWERS FOR PROBLEM SET: CHAPTER 1
5 7
1. (a) 18 (b) 10 (c) 0 (d) − (e)
4 4
(f) a 2 − 3a (g) 4 x 2 − 6 x (h) 2 x 2 − 6 x (i) x 2 + 3 x (j) x 2 − 3 x
1 3 1
(k) 2 − (l) 2
x x x − 3x
1
2. −
4( 4 + h )
3. (a) D = ℜ; R = ℜ (e) D = ℜ R = [0 , ∞)
;
(b) D = ( − ∞7 ]; R = [0 , ∞
, ) (f)
D = ( − ∞,−1) ∪ ( 1, ∞) ; R = ( − ∞,0 ) ∪ ( 0 , ∞)
(c) D = ℜ R = ( −∞,3]
; (g)
D = ( − ∞,−3 ) ∪ ( − 3 , ∞) ; R = ( − ∞,1) ∪ ( 1, ∞) (d) D = ℜ; R = ℜ (h)
D = ( − ∞,−3 ) ∪ ( − 3 , ∞) ; R = ( − ∞,1) ∪ ( 1, ∞)
f  g = ( x − 1) ; g  f = x 2 − 1
2
4. (a)
(b) f  g = 2 x ; g  f = 2 x −3 +3

13. BMM 104: ENGINEERING MATHEMATICS I Page 13 of 13
x +3 6
(c) f g = ;g  f = 4 −
3−x x
1 1
(d) f g = − 1; g  f =
(
x +1
3 3
) 3
x −1 +1
3
( )
(e) f  g = x ; g  f = x + 2x
2 2
(f) f  g = x; g  f = x
(g) f  g = 2; g  f = 4
(h) f  g = x; g  f = x
5. (a). g( x ) = x −1 D : x ≥ 0 ; R = y ≥ −1
(b). g( x ) = x + 2 D : x ≥ 0; R = y ≥ 2
1
(c). g( x ) = D : x > 0; R = y > 0
x2
(d). g( x ) = x 2 D : x ≤ 0; R = y ≥ 0
(e). g( x ) = x + 4 D : x ≥ −4 ; R = y ≥ 0
(f). g( x ) = 4 − x D : 0 ≤ x ≤ 4; R = 0 ≤ y ≤ 2
6. (a). Neither even nor odd (f) Even
(b) Neither even nor odd (g) Odd
(c) Neither even nor odd (h) Neither even nor odd
(d) Odd (i) Even
(e) Odd (j) Odd