1) O documento descreve diferentes tipos de funções elementares, incluindo funções constantes, identidade, lineares, do primeiro grau, módulo, quadráticas e racionais. 2) As funções constantes, identidade e lineares têm domínio R, enquanto funções do primeiro grau e quadráticas mapeiam R para R. 3) A função módulo mapeia R para [0, +∞) e funções racionais têm domínio excluindo valores que tornam o denominador zero.

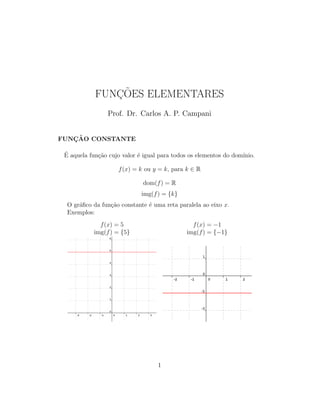
1. FUNC¸ ˜OES ELEMENTARES
Prof. Dr. Carlos A. P. Campani
FUNC¸ ˜AO CONSTANTE
´E aquela fun¸c˜ao cujo valor ´e igual para todos os elementos do dom´ınio.
f(x) = k ou y = k, para k ∈ R
dom(f) = R
img(f) = {k}
O gr´afico da fun¸c˜ao constante ´e uma reta paralela ao eixo x.
Exemplos:
f(x) = 5 f(x) = −1
img(f) = {5} img(f) = {−1}
1

2. FUNC¸ ˜AO IDENTIDADE
´E aquela fun¸c˜ao cujo valor para x ´e o pr´oprio x.
f(x) = x ou y = x
dom(f) = R
img(f) = R
FUNC¸ ˜AO LINEAR
f(x) = ax, a ∈ R e a = 0
dom(f) = R
img(f) = R
2

3. Exemplo: f(x) = 2x
FUNC¸ ˜AO DO 1o
GRAU OU AFIM
f(x) = ax + b com a, b ∈ R e a = 0
dom(f) = R e img(f) = R
Nesta fun¸c˜ao, a ´e o coeficiente angular e b ´e o coeficiente linear. O coeficiente
angular ´e o respons´avel pela inclina¸c˜ao da reta do gr´afico da fun¸c˜ao do 1o
grau. O coeficiente linear indica o ponto onde a reta intercepta o eixo y.
• a > 0: a fun¸c˜ao ´e crescente
• a < 0: a fun¸c˜ao ´e decrescente
3

4. Exemplos:
y = 2x + 3 y = −3x + 1
a > 0 (crescente) a < 0 (decrescente)
• Intercepta¸c˜ao do eixo x: obter as ra´ızes da equa¸c˜ao f(x) = 0 e os
pontos s˜ao todos os pontos (xi, 0) em que xi ´e raiz da equa¸c˜ao
• Intercepta¸c˜ao do eixo y: obter f(0) e o ponto de intercepta¸c˜ao ´e (0, f(0))
Observa¸c˜ao: este m´etodo pode ser aplicado em qualquer tipo de fun¸c˜ao para
obter as intercepta¸c˜oes.
Para os exemplos,
2x + 3 = 0 ⇒ x = −
3
2
(−3/2, 0)
f(0) = 2.0 + 3 = 3 (0, 3)
−3x + 1 = 0 ⇒ x =
1
3
(1/3, 0)
f(0) = −3.0 + 1 = 1 (0, 1)
4

5. FUNC¸ ˜OES CRESCENTES E DECRESCENTES
Uma fun¸c˜ao f : A → B, definida como y = f(x), ´e crescente se, para todo
x1, x2 ∈ dom(f), x1 < x2 → f(x1) < f(x2).
Ou seja, a inclina¸c˜ao m ´e positiva:
m =
f(x2) − f(x1)
x2 − x1
> 0
Uma fun¸c˜ao f : A → B, definida como y = f(x), ´e decrescente se, para
todo x1, x2 ∈ dom(f), x1 < x2 → f(x1) > f(x2).
Ou seja, a inclina¸c˜ao m ´e negativa:
m =
f(x2) − f(x1)
x2 − x1
< 0
INCLINAC¸ ˜AO E SINAL DA FUNC¸ ˜AO DO 1o
GRAU OU AFIM
Na fun¸c˜ao do 1o
grau, f(x) = ax + b, a inclina¸c˜ao da reta ´e o coeficiente
angular a:
m =
f(x2) − f(x1)
x2 − x1
=
ax2 + b − (ax1 + b)
x2 − x1
=
ax2 + b − ax1 − b
x2 − x1
=
=
ax2 − ax1
x2 − x1
=
a(x2 − x1)
x2 − x1
= a
Consideremos a fun¸c˜ao f(x) = ax + b, cuja raiz ´e ax + b = 0, x = −b/a.
Este ´e o valor em que a fun¸c˜ao troca de sinal. Se a > 0, a fun¸c˜ao ´e crescente
e os valores da fun¸c˜ao para x < −b/a s˜ao negativos e os para x > −b/a
s˜ao positivos. Se a < 0, a fun¸c˜ao ´e decrescente e os valores da fun¸c˜ao para
x < −b/a s˜ao positivos e os para x > −b/a s˜ao negativos.
FUNC¸ ˜AO M´ODULO OU VALOR ABSOLUTO
A fun¸c˜ao m´odulo ou valor absoluto,
f(x) = |x|
5

6. ´e uma fun¸c˜ao modular (por ter resultados alternativos) definida por:
|x| =
x se x ≥ 0
−x se x < 0
Com dom(f) = R e img(f) = [0, +∞).
FUNC¸ ˜AO QUADR´ATICA OU FUNC¸ ˜AO DO 2o
GRAU
f(x) = ax2
+ bx + c com a = 0
dom(f) = R
Os n´umeros a, b, c ∈ R s˜ao chamados de coeficientes da fun¸c˜ao. O coeficiente
a ´e chamado de coeficiente principal, e tem papel definitivo na determina¸c˜ao
da concavidade da fun¸c˜ao quadr´atica.
Exemplo: f(x) = x2
+ 2x − 3, onde a = 1, b = 2 e c = −3
6

7. GR´AFICO DA FUNC¸ ˜AO QUADR´ATICA
Os elementos que devem ser considerados para a determina¸c˜ao do gr´afico
da fun¸c˜ao f(x) = ax2
+ bc + c s˜ao os seguintes:
• A curva da fun¸c˜ao ´e uma par´abola com eixo de simetria paralelo ao
eixo y
• A interse¸c˜ao do eixo de simetria com a curva da par´abola ´e um ponto
chamado de v´ertice
• A intercepta¸c˜ao da curva do gr´afico ao eixo y ocorre em (0, f(0)), ou
seja, em (0, c)
• Se a > 0 a par´abola tem concavidade voltada para cima
• Se a < 0 a par´abola tem concavidade voltada para baixo
7

8. Exemplos:
y = x2
+ 2x − 3 y = −2x2
+ 5x + 1
a = 1 > 0 a = −2 < 0
• A intercepta¸c˜ao da curva do gr´afico ao eixo x ocorre nos zeros da
fun¸c˜ao, que s˜ao as ra´ızes da equa¸c˜ao a2
+ bx + c = 0, e os valores
s˜ao dados pela f´ormula de Baskara:
x =
−b ±
√
∆
2a
∆ = b2
− 4ac
Neste caso ocorrem trˆes possibilidades:
1. ∆ > 0: duas ra´ızes reais distintas (intercepta o eixo x em dois
pontos distintos)
2. ∆ = 0: ra´ızes idˆenticas (intercepta o eixo x em um ´unico ponto)
3. ∆ < 0: n˜ao h´a ra´ızes reais pois
√
∆ ∈ R se ∆ < 0 (n˜ao intercepta
o eixo x)
8

9. Toda fun¸c˜ao quadr´atica expressa na forma canˆonica y = ax2
+ bx + c,
a = 0, pode ser reescrita na seguinte forma canˆonica:
y = a(x − xv)2
+ yv
sendo
(xv, yv) = −
b
2a
, −
∆
4a
as coordenadas do v´ertice da par´abola, e o eixo de simetria ´e dado por x = xv.
Exemplo: Seja a fun¸c˜ao y = x2
− 6x + 5.
• y = (x2
− 6x) + 5 [prop. associativa]
• y = (x2
− 6x + 9) − 9 + 5 [completa¸c˜ao de quadrados]
• y = (x − 3)2
− 4 [produto not´avel e simplifica¸c˜ao]
Neste caso, xv = 3, yv = −4, e o eixo de simetria ´e x = 3.
CONSTRUINDO O GR´AFICO DA FUNC¸ ˜AO QUADR´ATICA
Para determinar o gr´afico da fun¸c˜ao quadr´atica devemos considerar:
• concavidade
• v´ertice
• eixo de simetria
• ra´ızes
Exemplo: Seja y = 2x2
+ 4x − 1.
Como a = 2 > 0, a concavidade ´e voltada para cima.
As coordenadas do v´ertice s˜ao:
(xv, yv) = −
4
2.2
, −
24
4.2
= (−1, −3)
Eixo de simetria ´e x = xv = −1.
As ra´ızes s˜ao x =
−4+
√
42−4.2.(−1)
2.2
≈ 0, 2247 e x =
−4−
√
42−4.2.(−1)
2.2
≈
−2, 2247.
9

10. IMAGEM DA FUNC¸ ˜AO QUADR´ATICA
Temos dois casos:
1. a < 0: como a concavidade ´e voltada para baixo, o v´ertice ´e o maior
valor da fun¸c˜ao, o que determina que img(f) = (−∞, − ∆
4a
]
2. a > 0: como a concavidade ´e voltada para cima, o v´ertice ´e o menor
valor da fun¸c˜ao, o que implica que img(f) = [− ∆
4a
, +∞)
FUNC¸ ˜AO POLINOMIAL
A fun¸c˜ao polinomial ´e definida como:
f(x) = a0xn
+ a1xn−1
+ a2xn−2
+ · · · + an−1x + an
onde n ´e chamado de grau da fun¸c˜ao, a0, a1, . . . , an ∈ R s˜ao chamados de
coeficientes e a0 = 0. O dom´ınio da fun¸c˜ao polinomial ´e R, dom(f) = R.
10

11. Exemplos:
1. f(x) = k, com k ∈ R (fun¸c˜ao constante) - fun¸c˜ao polinomial de grau
zero (n = 0)
2. f(x) = ax + b, com a, b ∈ R (fun¸c˜ao afim) - fun¸c˜ao polinomial do 1o
grau (n = 1)
3. f(x) = ax2
+ bx + c, com a, b, c ∈ R (fun¸c˜ao quadr´atica) - fun¸c˜ao
polinomial do 2o
grau (n = 2)
4. f(x) = 2x5
− 3x2
+ 5 - fun¸c˜ao polinomial do 5o
grau (n = 5)
FUNC¸ ˜AO RACIONAL
A fun¸c˜ao racional ´e definida como a raz˜ao
f(x) =
p(x)
q(x)
onde p(x) e q(x) s˜ao polinˆomios em x e q(x) = 0.
dom(f) = {x ∈ R|q(x) = 0}
Exemplos:
a) f(x) = x−1
x+1
, com dom(f) = R − {−1}
b) f(x) = 2x
x2−9
, com dom(f) = R − {−3, 3} pois −3 e 3 s˜ao ra´ızes do
polinˆomio do denominador
CONSTRUC¸ ˜AO E AN´ALISE DO GR´AFICO DA FUNC¸ ˜AO DO
EXEMPLO
Seja f(x) = x−1
x+1
. J´a sabemos que dom(f) = R − {−1}, pois x + 1 = 0 tem
como raiz x = −1.
A fun¸c˜ao f intercepta o eixo y em (0, −1) pois f(0) = 0−1
0+1
= −1, e
intercepta o eixo x nas ra´ızes da equa¸c˜ao f(x) = 0, cuja solu¸c˜ao ´e a raiz do
numerador, x − 1 = 0, que ´e x = 1. Conclui-se que a fun¸c˜ao intercepta o
eixo x em apenas um ponto, o ponto (1, 0).
11

12. ASS´INTOTAS
Como a fun¸c˜ao n˜ao est´a definida em x = −1, devemos estudar o compor-
tamento da fun¸c˜ao nas vizinhan¸cas de x = −1.
“Vizinhan¸ca” aqui denota os n´umeros que est˜ao muito pr´oximos do n´u-
mero −1, tanto `a esquerda, ou seja, para os n´umeros menores que −1, quanto
`a direita, ou seja, para os n´umeros maiores que −1. Devemos observar que
os n´umeros da vizinhan¸ca, por mais pr´oximos que estejam de −1, jamais po-
dem assumir este valor. Podemos entender a vizinhan¸ca como um caminhar
ilimitado, sobre a reta R, em dire¸c˜ao ao n´umero −1, pela esquerda ou pela
direita, sem jamais l´a chegar.
• Caminhando pela esquerda em dire¸c˜ao ao n´umero −1 (por valores me-
nores que −1): −2, −1, 5, −1, 1, −1, 01, −1, 001, . . . Chamamos isso de
aproxima¸c˜ao pela esquerda.
• Caminhando pela direita em dire¸c˜ao ao n´umero −1 (por valores maio-
res que −1): −0, 5, −0, 9, −0, 99, −0, 999, . . . Chamamos isso de apro-
xima¸c˜ao pela direita.
A seguinte tabela mostra os valores da fun¸c˜ao para a aproxima¸c˜ao pela
esquerda, para a fun¸c˜ao dada:
x f(x)
−1, 1 −1,1−1
−1,1+1
= 21
−1, 01 −1,01−1
−1,01+1
= 201
−1, 001 −1,001−1
−1,001+1
= 2001
−1, 0001 −1,0001−1
−1,0001+1
= 20001
...
...
Ou seja, quanto mais pr´oximo de −1 pela esquerda, maior o valor da
fun¸c˜ao em valor absoluto, com sinal positivo.
12

13. Isso pode ser expresso usando a nota¸c˜ao de limites:
x → −1−
⇒ f(x) → +∞
Isso pode ser lido como:“quando x se aproxima de −1 pela esquerda, isso
implica que f(x) tende para +∞”.
Ou ent˜ao, podemos usar a seguinte nota¸c˜ao:
lim
x→−1−
f(x) = +∞
Isso pode ser lido como: “o limite de f(x) quando x se aproxima de (ou
tende para) −1 pela esquerda ´e +∞”.
A seguinte tabela mostra os valores da fun¸c˜ao para a aproxima¸c˜ao pela
direita, para a fun¸c˜ao dada:
x f(x)
−0, 9 −0,9−1
−0,9+1
= −19
−0, 99 −0,99−1
−0,99+1
= −199
−0, 999 −0,999−1
−0,999+1
= −1999
−0, 9999 −0,9999−1
−0,9999+1
= −19999
...
...
Ou seja, quanto mais pr´oximo de −1 pela direita, maior o valor da fun¸c˜ao
em valor absoluto, com sinal negativo.
Isso pode ser expresso usando a nota¸c˜ao de limites:
x → −1+
⇒ f(x) → −∞
Isso pode ser lido como:“quando x se aproxima de −1 pela direita, isso
implica que f(x) tende para −∞”.
Ou ent˜ao, podemos usar a seguinte nota¸c˜ao:
lim
x→−1+
f(x) = −∞
Isso pode ser lido como: “o limite de f(x) quando x se aproxima de (ou
tende para) −1 pela direita ´e −∞”.
13

14. No gr´afico da fun¸c˜ao, estes dois limites ser˜ao percebidos como a curva da
fun¸c˜ao tangenciando a reta vertical x = −1, indo para +∞ no lado esquerdo
e para −∞ do lado direito da reta, como mostra a figura:
O n´umero −1 ´e uma descontinuidade infinita, pelo valor da fun¸c˜ao no
ponto estar indefinido e nas proximidades do ponto a fun¸c˜ao assumir valor
infinito. A reta vertical x = −1 ´e chamada de ass´ıntota vertical da fun¸c˜ao.
Isso conclui o que chamamos de an´alise de ass´ıntotas verticais.
Agora, precisamos analisar o que ocorre com a fun¸c˜ao para valores muito
grandes, tanto positivos quanto negativos. Ou seja, precisamos fazer a an´alise
do comportamento da fun¸c˜ao nos extremos do eixo x.
14

15. Vamos come¸car analisando os valores da fun¸c˜ao quando x cresce ilimita-
damente para valores positivos. A seguinte tabela mostra os valores que a
fun¸c˜ao dada assume quando x cresce para +∞:
x f(x)
10 10−1
10+1
≈ 0, 8181
100 100−1
100+1
≈ 0, 9801
1000 1000−1
1000+1
≈ 0, 998
10000 10000−1
10000+1
≈ 0, 9998
...
...
Isso sugere que o valor da fun¸c˜ao se aproxima de 1, por valores menores
que 1. Podemos usar a seguinte nota¸c˜ao para expressar isso:
x → +∞ ⇒ f(x) → 1−
Isso pode ser lido como: “quando x tende para +∞, o valor de f(x) se
aproxima de 1 por baixo”.
Ou ent˜ao, podemos usar a seguinte nota¸c˜ao:
lim
x→+∞
f(x) = 1−
Isso pode ser lido como: “o limite de f(x) quando x tende para +∞ ´e
igual a 1, com f(x) aproximando-se de 1 por baixo”.
Agora fazemos a mesma coisa para x tendendo para −∞:
x f(x)
−10 −10−1
−10+1
≈ 1, 2222
−100 −100−1
−100+1
≈ 1, 0202
−1000 −1000−1
−1000+1
≈ 1, 0020
−10000 −10000−1
−10000+1
≈ 1, 0002
...
...
15

16. Isso significa que o valor da fun¸c˜ao se aproxima de 1, por valores maiores
que 1. Podemos usar a seguinte nota¸c˜ao para expressar isso:
x → −∞ ⇒ f(x) → 1+
Isso pode ser lido como: “quando x tende para −∞, o valor de f(x) se
aproxima de 1 por cima”.
Ou ent˜ao, podemos usar a seguinte nota¸c˜ao:
lim
x→−∞
f(x) = 1+
Isso pode ser lido como: “o limite de f(x) quando x tende para −∞ ´e
igual a 1, com f(x) aproximando-se de 1 por cima”.
No gr´afico da fun¸c˜ao, estes dois limites, x → +∞ e x → −∞, ser˜ao
percebidos como a curva da fun¸c˜ao tangenciando a reta horizontal y = 1,
aproximando-se o valor da fun¸c˜ao de 1, por cima e por baixo, como mostra
a figura:
A reta horizontal y = 1 ´e chamada de ass´ıntota horizontal da fun¸c˜ao.
E isso completa a an´alise do comportamento da fun¸c˜ao nos extremos do
eixo x.
16

17. ARTICULANDO TODOS OS RESULTADOS NO GR´AFICO
Sobre a fun¸c˜ao f(x) = x−1
x+1
sabemos que ela possui uma indetermina¸c˜ao
infinita em x = −1, onde ocorre uma ass´ıntota vertical, que cruza o eixo x
em x = 1 e o eixo y em y = −1. Al´em disto, sabemos que ela possui uma
ass´ıntota horizontal em y = 1. Combinando todas as informa¸c˜oes podemos
obter facilmente o gr´afico completo da fun¸c˜ao, apresentado na imagem acima.
17