![El problema solicita 𝑇𝑇 para un cierto 𝑅𝑅. Interesa, por tanto, hallar la dependencia inversa
𝑇𝑇(𝑅𝑅). Para ello, de forma análoga a la resolución del sistema de ecuaciones, evaluamos el
logaritmo natural de los dos miembros y despejamos 𝑇𝑇:
𝑇𝑇(𝑅𝑅) =
𝐵𝐵
ln(𝑅𝑅 𝑅𝑅0⁄ )
Finalmente, calculamos 𝑇𝑇 para 𝑅𝑅 = 1004.5 Ω:
𝑇𝑇(1004.5) =
−119.3 K
ln(1004.5 Ω 1452.6 Ω⁄ )
= 323.4 K
2.- Expresar en grados Kelvin una temperatura de −18 °F.
La escala Fahrenheit asigna las temperaturas 32 °F y 212 °F a los puntos de fusión y ebullición
del agua, respectivamente. Así, la relación entre una misma temperatura expresada en las
escalas Fahrenheit y Kelvin es la siguiente:
𝑋𝑋(K) − 273.15
373.15 − 273.15
=
𝑋𝑋(°F) − 32
212 − 32
⟹ 𝑋𝑋(K) =
5
9
[𝑋𝑋(°F) − 32] + 273.15
Sin más que sustituir:
5
9
[−18 − 32] + 273.15 = 245.4 K
3.- Supongamos que en lugar de definir la temperatura 𝜃𝜃 como una función lineal de una variable
termométrica 𝑋𝑋 se define la temperatura 𝜃𝜃∗
como una función logarítmica 𝜃𝜃∗
= 𝑎𝑎 ln 𝑋𝑋 + 𝑏𝑏, siendo 𝑎𝑎 y 𝑏𝑏 dos
constantes a determinar mediante la elección de dos puntos fijos. Supongamos que se escoge como variable
termométrica la longitud 𝐿𝐿 de una columna de líquido en un termómetro de vidrio, siendo 𝐿𝐿 = 5 cm cuando
𝜃𝜃∗
= 0 °C y 𝐿𝐿 = 25 cm para 𝜃𝜃∗
= 100 °C. Calcular la distancia existente entre las divisiones
correspondientes a 0 °C y 10 °C. Calcular la distancia existente entre las divisiones correspondientes a
90 °C y 100 °C.
En primer lugar, calculamos el valor de los parámetros 𝑎𝑎 y 𝑏𝑏 a partir de la información que
suministra el enunciado. Planteamos el sistema de ecuaciones lineales:
�
𝜃𝜃1
∗
= 𝑎𝑎 ln 𝐿𝐿1 + 𝑏𝑏
𝜃𝜃2
∗
= 𝑎𝑎 ln 𝐿𝐿2 + 𝑏𝑏
Siendo 𝜃𝜃1
∗
= 0 °C, 𝜃𝜃2
∗
= 100 °C, 𝐿𝐿1 = 5 cm y 𝐿𝐿2 = 25 cm. La solución de este sistema viene dada
por las expresiones:
𝑎𝑎 =
𝜃𝜃1
∗
− 𝜃𝜃2
∗
ln(𝐿𝐿1 𝐿𝐿2⁄ )
𝑏𝑏 = 𝜃𝜃1
∗
− 𝑎𝑎 ln 𝐿𝐿1
Introducimos los datos:
𝑎𝑎 =
0 °C − 100 °C
ln(5 cm 25 cm⁄ )
= 62.1 °C
𝑏𝑏 = 0 °C − (62.1 °C) ⋅ ln(5 cm) = −100 °C
Ya conocemos la función temperatura:
𝜃𝜃∗
(°C) = 62.1 ln 𝐿𝐿(cm) − 100
MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Empfohlen
Empfohlen
Weitere ähnliche Inhalte
Was ist angesagt?
Was ist angesagt? (20)
Andere mochten auch
Andere mochten auch (14)
Ähnlich wie Termodinámica - Problemas resueltos
Ähnlich wie Termodinámica - Problemas resueltos (20)
Mehr von Martín de la Rosa Díaz
Mehr von Martín de la Rosa Díaz (8)
Kürzlich hochgeladen
Kürzlich hochgeladen (20)
Termodinámica - Problemas resueltos
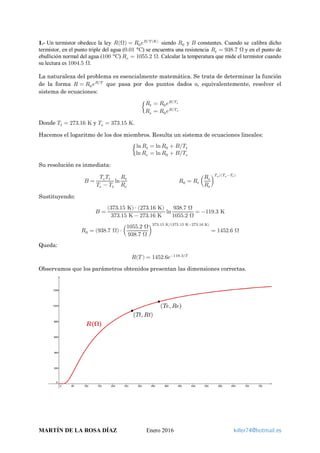
- 1. 1.- Un termistor obedece la ley 𝑅𝑅(Ω) = 𝑅𝑅0 𝑒𝑒 𝐵𝐵 𝑇𝑇(𝐾𝐾)⁄ siendo 𝑅𝑅0 y 𝐵𝐵 constantes. Cuando se calibra dicho termistor, en el punto triple del agua (0.01 °C) se encuentra una resistencia 𝑅𝑅𝑡𝑡 = 938.7 Ω y en el punto de ebullición normal del agua (100 °C) 𝑅𝑅𝑒𝑒 = 1055.2 Ω. Calcular la temperatura que mide el termistor cuando su lectura es 1004.5 Ω. La naturaleza del problema es esencialmente matemática. Se trata de determinar la función de la forma 𝑅𝑅 = 𝑅𝑅0 𝑒𝑒 𝐵𝐵 𝑇𝑇⁄ que pasa por dos puntos dados o, equivalentemente, resolver el sistema de ecuaciones: � 𝑅𝑅𝑡𝑡 = 𝑅𝑅0 𝑒𝑒 𝐵𝐵 𝑇𝑇𝑡𝑡⁄ 𝑅𝑅𝑒𝑒 = 𝑅𝑅0 𝑒𝑒 𝐵𝐵 𝑇𝑇𝑒𝑒⁄ Donde 𝑇𝑇𝑡𝑡 = 273.16 K y 𝑇𝑇𝑒𝑒 = 373.15 K. Hacemos el logaritmo de los dos miembros. Resulta un sistema de ecuaciones lineales: � ln 𝑅𝑅𝑡𝑡 = ln 𝑅𝑅0 + 𝐵𝐵 𝑇𝑇𝑡𝑡⁄ ln 𝑅𝑅𝑒𝑒 = ln 𝑅𝑅0 + 𝐵𝐵 𝑇𝑇𝑒𝑒⁄ Su resolución es inmediata: 𝐵𝐵 = 𝑇𝑇𝑒𝑒 𝑇𝑇𝑡𝑡 𝑇𝑇𝑒𝑒 − 𝑇𝑇𝑡𝑡 ln 𝑅𝑅𝑡𝑡 𝑅𝑅𝑒𝑒 𝑅𝑅0 = 𝑅𝑅𝑡𝑡 � 𝑅𝑅𝑒𝑒 𝑅𝑅𝑡𝑡 � 𝑇𝑇𝑒𝑒 (𝑇𝑇𝑒𝑒−𝑇𝑇𝑡𝑡)⁄ Sustituyendo: 𝐵𝐵 = (373.15 K) ⋅ (273.16 K) 373.15 K − 273.16 K ln 938.7 Ω 1055.2 Ω = −119.3 K 𝑅𝑅0 = (938.7 Ω) ⋅ � 1055.2 Ω 938.7 Ω � 373.15 K (373.15 K−273.16 K)⁄ = 1452.6 Ω Queda: 𝑅𝑅(𝑇𝑇 ) = 1452.6𝑒𝑒−119.3 𝑇𝑇⁄ Observamos que los parámetros obtenidos presentan las dimensiones correctas. MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 2. El problema solicita 𝑇𝑇 para un cierto 𝑅𝑅. Interesa, por tanto, hallar la dependencia inversa 𝑇𝑇(𝑅𝑅). Para ello, de forma análoga a la resolución del sistema de ecuaciones, evaluamos el logaritmo natural de los dos miembros y despejamos 𝑇𝑇: 𝑇𝑇(𝑅𝑅) = 𝐵𝐵 ln(𝑅𝑅 𝑅𝑅0⁄ ) Finalmente, calculamos 𝑇𝑇 para 𝑅𝑅 = 1004.5 Ω: 𝑇𝑇(1004.5) = −119.3 K ln(1004.5 Ω 1452.6 Ω⁄ ) = 323.4 K 2.- Expresar en grados Kelvin una temperatura de −18 °F. La escala Fahrenheit asigna las temperaturas 32 °F y 212 °F a los puntos de fusión y ebullición del agua, respectivamente. Así, la relación entre una misma temperatura expresada en las escalas Fahrenheit y Kelvin es la siguiente: 𝑋𝑋(K) − 273.15 373.15 − 273.15 = 𝑋𝑋(°F) − 32 212 − 32 ⟹ 𝑋𝑋(K) = 5 9 [𝑋𝑋(°F) − 32] + 273.15 Sin más que sustituir: 5 9 [−18 − 32] + 273.15 = 245.4 K 3.- Supongamos que en lugar de definir la temperatura 𝜃𝜃 como una función lineal de una variable termométrica 𝑋𝑋 se define la temperatura 𝜃𝜃∗ como una función logarítmica 𝜃𝜃∗ = 𝑎𝑎 ln 𝑋𝑋 + 𝑏𝑏, siendo 𝑎𝑎 y 𝑏𝑏 dos constantes a determinar mediante la elección de dos puntos fijos. Supongamos que se escoge como variable termométrica la longitud 𝐿𝐿 de una columna de líquido en un termómetro de vidrio, siendo 𝐿𝐿 = 5 cm cuando 𝜃𝜃∗ = 0 °C y 𝐿𝐿 = 25 cm para 𝜃𝜃∗ = 100 °C. Calcular la distancia existente entre las divisiones correspondientes a 0 °C y 10 °C. Calcular la distancia existente entre las divisiones correspondientes a 90 °C y 100 °C. En primer lugar, calculamos el valor de los parámetros 𝑎𝑎 y 𝑏𝑏 a partir de la información que suministra el enunciado. Planteamos el sistema de ecuaciones lineales: � 𝜃𝜃1 ∗ = 𝑎𝑎 ln 𝐿𝐿1 + 𝑏𝑏 𝜃𝜃2 ∗ = 𝑎𝑎 ln 𝐿𝐿2 + 𝑏𝑏 Siendo 𝜃𝜃1 ∗ = 0 °C, 𝜃𝜃2 ∗ = 100 °C, 𝐿𝐿1 = 5 cm y 𝐿𝐿2 = 25 cm. La solución de este sistema viene dada por las expresiones: 𝑎𝑎 = 𝜃𝜃1 ∗ − 𝜃𝜃2 ∗ ln(𝐿𝐿1 𝐿𝐿2⁄ ) 𝑏𝑏 = 𝜃𝜃1 ∗ − 𝑎𝑎 ln 𝐿𝐿1 Introducimos los datos: 𝑎𝑎 = 0 °C − 100 °C ln(5 cm 25 cm⁄ ) = 62.1 °C 𝑏𝑏 = 0 °C − (62.1 °C) ⋅ ln(5 cm) = −100 °C Ya conocemos la función temperatura: 𝜃𝜃∗ (°C) = 62.1 ln 𝐿𝐿(cm) − 100 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 3. Nuestra pretensión consiste en hallar las diferencias de longitudes correspondientes a dos intervalos de temperatura, por lo que conviene encontrar explícitamente la relación 𝐿𝐿(𝜃𝜃∗ ), que es la inversa de 𝜃𝜃∗ (𝐿𝐿): 𝑒𝑒𝜃𝜃∗ = 𝑒𝑒𝑎𝑎ln 𝐿𝐿+𝑏𝑏 = 𝑒𝑒𝑎𝑎ln 𝐿𝐿 𝑒𝑒𝑏𝑏 = 𝑒𝑒𝑏𝑏 𝐿𝐿𝑎𝑎 ⟹ 𝐿𝐿(𝜃𝜃∗ ) = (𝑒𝑒𝜃𝜃∗ 𝑒𝑒𝑏𝑏 ⁄ )1 𝑎𝑎⁄ = 5𝑒𝑒𝜃𝜃∗ 62.1⁄ El incremento ∆𝐿𝐿 ligado a una variación en la temperatura ∆𝜃𝜃∗ = 𝜃𝜃2 ∗ − 𝜃𝜃1 ∗ tiene por expresión: ∆𝐿𝐿 = 5�𝑒𝑒𝜃𝜃2 ∗ 62.1⁄ − 𝑒𝑒𝜃𝜃1 ∗ 62.1⁄ � Obtenemos los incrementos que solicita el problema: ∆𝐿𝐿1 = 5�𝑒𝑒10 62.1⁄ − 𝑒𝑒0 62.1⁄ � = 0.87 cm ∆𝐿𝐿2 = 5�𝑒𝑒100 62.1⁄ − 𝑒𝑒90 62.1⁄ � = 3.72 cm Observamos que ∆𝐿𝐿2 > ∆𝐿𝐿1. Así, el termómetro calibrado con esta escala logarítmica será más sensible en el intervalo 90 °C − 100 °C, donde ∆𝐿𝐿2 ∆𝜃𝜃2 ∗ ⁄ ≅ 0.37 cm °C⁄ , que en la franja 0 °C − 10 °C, en la que ∆𝐿𝐿1 ∆𝜃𝜃1 ∗ ⁄ ≅ 0.09 cm °C⁄ . En efecto, como la derivada de 𝐿𝐿(𝜃𝜃∗ ), 𝑑𝑑𝑑𝑑 𝑑𝑑⁄ 𝜃𝜃∗ = 0.08𝑒𝑒𝜃𝜃∗ 62.1⁄ , es una función monótona creciente, las variaciones ∆𝐿𝐿 correspondientes a intervalos de temperatura ∆𝜃𝜃∗ = 𝜃𝜃2 ∗ − 𝜃𝜃1 ∗ tales que 𝜃𝜃2 ∗ − 𝜃𝜃1 ∗ es constante se incrementarán a medida que avancemos en el sentido de crecimiento de 𝜃𝜃∗ . MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 4. 4.- Un termómetro de mercurio cuyo capilar se halla totalmente lleno a 50 ºC, se calienta hasta 52 ºC. El coeficiente de dilatación del mercurio es 1.8·10-4 K-1 y su coeficiente de compresibilidad, 3.9·10-6 atm-1 , siendo 8.5·10-6 ºC-1 el coeficiente de dilatación del vidrio. Calcular la presión que desarrolla el mercurio en el capilar. Una variación elemental en la presión del mercurio se puede poner en función de las otras dos coordenadas termodinámicas, 𝑉𝑉 y 𝑇𝑇: 𝑑𝑑𝑑𝑑 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 𝑑𝑑𝑑𝑑 + � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 𝑑𝑑𝑑𝑑 O bien, en términos de los coeficientes termodinámicos del mercurio: 𝑑𝑑𝑑𝑑 = 1 𝛽𝛽 𝑚𝑚,Hg 𝑝𝑝 𝑑𝑑𝑑𝑑 − 1 𝜅𝜅𝑇𝑇 ,Hg 𝑉𝑉 𝑑𝑑𝑑𝑑 = 𝛼𝛼Hg 𝜅𝜅𝑇𝑇 ,Hg 𝑑𝑑𝑑𝑑 − 1 𝜅𝜅𝑇𝑇 ,Hg 𝑉𝑉 𝑑𝑑𝑑𝑑 Al hallarse el mercurio contenido en la cavidad del termómetro, la variación de volumen que experimenta está en todo momento limitada por el tamaño de la citada cavidad, que también se expande a causa del incremento de temperatura. Al tratarse de un fluido, el mercurio se dilata más que el vidrio, de forma que su volumen será el mismo que el de la cavidad del termómetro. Por tanto: 𝑑𝑑𝑑𝑑 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 𝑑𝑑𝑑𝑑 = 𝛼𝛼vidrio 𝑉𝑉𝑉𝑉𝑉𝑉 De esta forma: 𝑑𝑑𝑑𝑑 = 𝛼𝛼Hg 𝜅𝜅𝑇𝑇 ,Hg 𝑑𝑑𝑑𝑑 − 𝛼𝛼vidrio 𝜅𝜅𝑇𝑇 ,Hg 𝑑𝑑𝑑𝑑 ⟹ ∆𝑝𝑝 = 𝛼𝛼Hg − 𝛼𝛼vidrio 𝜅𝜅𝑇𝑇 ,Hg ∆𝑇𝑇 Sustituyendo valores numéricos: ∆𝑝𝑝 = 1.8 ⋅ 10−4 K−1 − 8.5 ⋅ 10−6 K−1 3.9 ⋅ 10−6 atm−1 ⋅ (2 K) = 87.9 atm 5.- Escribir las seis derivadas parciales de la entalpía que pueden expresarse en función de p,V,T. Determinar su valor para un mol de gas ideal en función de cv y las variables de estado. Aplicando la definición de entalpía, la regla de la cadena y otras propiedades de las derivadas parciales, se tiene: � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = 𝐶𝐶𝑝𝑝 ¿ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 ? 𝐻𝐻 = 𝐻𝐻(𝑇𝑇, 𝑝𝑝) ⟹ 𝑑𝑑𝑑𝑑 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 𝑑𝑑𝑑𝑑 + � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑 = 𝛿𝛿𝛿𝛿 + 𝑉𝑉𝑉𝑉𝑉𝑉 ⟹ 𝛿𝛿𝛿𝛿 = 𝑑𝑑𝑑𝑑 − 𝑉𝑉𝑉𝑉𝑉𝑉 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 𝑑𝑑𝑑𝑑 + �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � 𝑑𝑑𝑑𝑑 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 5. 𝑑𝑑𝑑𝑑 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 𝑑𝑑𝑑𝑑 + � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 𝑑𝑑𝑑𝑑 ⟹ 𝛿𝛿𝛿𝛿 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 𝑑𝑑𝑑𝑑 + �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 𝑑𝑑𝑑𝑑 + � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 𝑑𝑑𝑑𝑑� = �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝑑𝑑𝑑𝑑 + ��� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝑑𝑑𝑑𝑑 𝑉𝑉 = cte ⟹ 𝛿𝛿𝑄𝑄𝑣𝑣 𝑑𝑑𝑑𝑑 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 ⎩ �� ⎨ �� ⎧ 𝛿𝛿𝑄𝑄𝑣𝑣 𝑑𝑑𝑑𝑑 = 𝐶𝐶𝑣𝑣 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = 𝐶𝐶𝑝𝑝 ⟹ 𝐶𝐶𝑣𝑣 − 𝐶𝐶𝑝𝑝 = �� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝐶𝐶𝑣𝑣 − 𝐶𝐶𝑝𝑝� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 + 𝑉𝑉 ¿ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 ? I) � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝐶𝐶𝑝𝑝 − 𝐶𝐶𝑣𝑣� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 − 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = � 𝜕𝜕(𝐻𝐻 − 𝑝𝑝𝑝𝑝 ) 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − � 𝜕𝜕(𝑝𝑝𝑝𝑝 ) 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 − 𝑝𝑝 = �𝐶𝐶𝑝𝑝 − 𝐶𝐶𝑣𝑣� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 − 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝐶𝐶𝑝𝑝 − 𝐶𝐶𝑣𝑣� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 II) � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = ��𝐶𝐶𝑣𝑣 − 𝐶𝐶𝑝𝑝�� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 + 𝑉𝑉 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝐶𝐶𝑣𝑣 − 𝐶𝐶𝑝𝑝�� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = −1 ⟹ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = − � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝐶𝐶𝑝𝑝 − 𝐶𝐶𝑣𝑣� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 6. ¿ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 ? � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = � 𝜕𝜕(𝑈𝑈 + 𝑝𝑝𝑝𝑝 ) 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 + � 𝜕𝜕(𝑝𝑝𝑝𝑝 ) 𝜕𝜕𝜕𝜕 � 𝑉𝑉 ⎩ �� ⎨ �� ⎧ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = 𝐶𝐶𝑣𝑣 � 𝜕𝜕(𝑝𝑝𝑝𝑝 ) 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = 𝐶𝐶𝑣𝑣 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 ¿ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 ? � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = 𝐶𝐶𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 ¿ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 ? � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = ��𝐶𝐶𝑝𝑝 − 𝐶𝐶𝑣𝑣� � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 � � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 Determinemos el valor de las derivadas parciales calculadas para un mol de gas ideal: � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = 𝑐𝑐𝑝𝑝 =⏞ 𝑐𝑐𝑝𝑝−𝑐𝑐𝑣𝑣=𝑅𝑅 𝑐𝑐𝑣𝑣 + 𝑅𝑅 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝑐𝑐𝑣𝑣 − 𝑐𝑐𝑝𝑝�� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 + 𝑉𝑉 =⏞ 𝑇𝑇 = 𝑝𝑝𝑝𝑝 𝑅𝑅 �𝑐𝑐𝑣𝑣 − 𝑐𝑐𝑝𝑝� 𝑉𝑉 𝑅𝑅 + 𝑉𝑉 =⏞ 𝑐𝑐𝑣𝑣−𝑐𝑐𝑝𝑝=−𝑅𝑅 0 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = �𝑐𝑐𝑝𝑝 − 𝑐𝑐𝑣𝑣�� 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 =⏞ 𝑇𝑇 = 𝑝𝑝𝑝𝑝 𝑅𝑅 ∧ 𝑝𝑝= 𝑅𝑅𝑅𝑅 𝑉𝑉 �𝑐𝑐𝑝𝑝 − 𝑐𝑐𝑣𝑣� 𝑝𝑝 𝑅𝑅 + 𝑉𝑉 �− 𝑅𝑅𝑅𝑅 𝑉𝑉 2 � =⏞ 𝑐𝑐𝑝𝑝−𝑐𝑐𝑣𝑣=𝑅𝑅 𝑝𝑝 − 𝑅𝑅𝑅𝑅 𝑉𝑉 = 0 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = 𝑐𝑐𝑣𝑣 + 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 =⏞ 𝑝𝑝= 𝑅𝑅𝑅𝑅 𝑉𝑉 𝑐𝑐𝑣𝑣 + 𝑉𝑉 𝑅𝑅 𝑉𝑉 = 𝑐𝑐𝑣𝑣 + 𝑅𝑅 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 = 𝑐𝑐𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑝𝑝 =⏞ 𝑇𝑇 = 𝑝𝑝𝑝𝑝 𝑅𝑅 𝑐𝑐𝑝𝑝 𝑝𝑝 𝑅𝑅 =⏞ 𝑐𝑐𝑝𝑝−𝑐𝑐𝑣𝑣=𝑅𝑅 (𝑐𝑐𝑣𝑣 + 𝑅𝑅) 𝑝𝑝 𝑅𝑅 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 7. � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 = � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑉𝑉 =⏞ 𝑇𝑇 = 𝑝𝑝𝑝𝑝 𝑅𝑅 (𝑐𝑐𝑣𝑣 + 𝑅𝑅) 𝑉𝑉 𝑅𝑅 6.- Un sistema constituido por dos moles de un gas de Clausius, cuya ecuación térmica es 𝑝𝑝(𝑣𝑣 − 𝑏𝑏) = 𝑅𝑅𝑅𝑅, siendo 𝑏𝑏 = 0.0221 litros mol⁄ , se encuentra inicialmente a la presión de 24 atm y se expande adiabáticamente contra una presión exterior constante 𝑝𝑝0 = 1 atm. En un segundo proceso entre los mismos estados inicial y final, la presión se reduce de forma cuasiestática cumpliendo la ecuación 𝑝𝑝 = 𝑝𝑝0 𝑏𝑏 𝑣𝑣⁄ . Si la temperatura del estado inicial es 300 K y la del estado final es 290 K, calcular la cantidad de calor intercambiada por el sistema en este segundo proceso. La variación de energía interna es la misma para los dos procesos, pues tanto sus estados iniciales como sus estados finales coinciden. Además, el calor intercambiado durante el primer proceso es cero al ser este adiabático. De esta forma, el calor pedido vale: � ∆𝑈𝑈 = −𝑊𝑊1 ∆𝑈𝑈 = 𝑄𝑄 − 𝑊𝑊2 ⟹ 𝑄𝑄 = 𝑊𝑊2 − 𝑊𝑊1 Calculemos el trabajo efectuado en los dos procesos, teniendo en cuenta que 𝑉𝑉 = 𝑛𝑛𝑛𝑛. El primero es una expansión contra una presión exterior constante: 𝑊𝑊1 = 𝑛𝑛 � 𝑝𝑝ext 𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛𝑝𝑝0 � 𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛𝑝𝑝0�𝑣𝑣𝑓𝑓 − 𝑣𝑣𝑖𝑖� En lo que respecta al segundo proceso, sabemos cómo varía la presión del sistema (que coincide en todo momento con la exterior, por ser la transformación cuasiestática) con el volumen: 𝑊𝑊2 = 𝑛𝑛� 𝑝𝑝𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛 � 𝑝𝑝0 𝑏𝑏 𝑣𝑣 𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛𝑝𝑝0 𝑏𝑏 � 𝑑𝑑𝑑𝑑 𝑣𝑣 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛𝑝𝑝0 𝑏𝑏�ln 𝑣𝑣𝑓𝑓 − ln 𝑣𝑣𝑖𝑖� Para calcular estos trabajos, necesitamos los volúmenes inicial y final, que obtenemos de la ecuación térmica: 𝑝𝑝(𝑣𝑣 − 𝑏𝑏) = 𝑅𝑅𝑅𝑅 ⟹ 𝑣𝑣 = 𝑅𝑅𝑅𝑅 𝑝𝑝 + 𝑏𝑏 ⎩ �� ⎨ �� ⎧ 𝑣𝑣𝑖𝑖 = 0.082 atmL Kmol ⋅ 300 K 24 atm + 0.0221 L mol = 1.05 L mol 𝑣𝑣𝑓𝑓 = 0.082 atmL Kmol ⋅ 290 K 1 atm + 0.0221 L mol = 23.8 L mol Finalmente, el calor es: 𝑄𝑄 = 2 mol ⋅ 1 atm ⋅ �0.0221 L mol ⋅ (ln 23.8 − ln 1.05) − 23.8 L mol + 1.05 L mol � = −45.4 atmL MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 8. 7.- Los coeficientes de compresibilidad isoterma, 𝜅𝜅𝑇𝑇 , y piezotérmico, 𝛽𝛽, de cierto gas vienen dados por las expresiones 𝜅𝜅𝑇𝑇 = 𝑣𝑣2 [𝑅𝑅𝑅𝑅(𝑣𝑣 + 2𝑏𝑏)]⁄ y 𝛽𝛽 = 1 𝑇𝑇⁄ , con 𝑏𝑏 = 0.04 litros mol⁄ . Si para valores elevados del volumen molar, v, el gas se comporta como un gas ideal, calcular (a) la ecuación térmica de estado de dicho gas y (b) el coeficiente de dilatación cúbica, 𝛼𝛼, cuando el volumen molar a 300 K es de 1 litro. a) Obtendremos la ecuación térmica mediante la integración de los coeficientes termodinámicos que proporciona el enunciado. Por una parte, el coeficiente piezotérmico 𝛽𝛽 se define como: 𝛽𝛽 = 1 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑣𝑣 Para el gas del enunciado: 1 𝑝𝑝 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑣𝑣 = 1 𝑇𝑇 ⟹ 𝑑𝑑𝑑𝑑 𝑇𝑇 = 𝑑𝑑𝑑𝑑 𝑝𝑝 ⟹ ln 𝑇𝑇 = ln 𝑝𝑝 + 𝑔𝑔1(𝑣𝑣) ⟹ 𝑝𝑝 = 𝑇𝑇 𝑒𝑒𝑔𝑔1(𝑣𝑣) = 𝑇𝑇𝑇𝑇(𝑣𝑣) Desconocemos la forma de 𝑔𝑔(𝑣𝑣), por lo que recurrimos al otro coeficiente termodinámico del que disponemos, 𝜅𝜅𝑇𝑇 . Derivando 𝑝𝑝 = 𝑇𝑇𝑇𝑇(𝑣𝑣) respecto del volumen: � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = 𝑇𝑇𝑇𝑇′(𝑣𝑣) De la definición de 𝜅𝜅𝑇𝑇 se desprende que: 𝜅𝜅𝑇𝑇 = − 1 𝑣𝑣 � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 ⟹ � 𝜕𝜕𝜕𝜕 𝜕𝜕𝜕𝜕 � 𝑇𝑇 = − 1 𝜅𝜅𝑇𝑇 𝑣𝑣 Por tanto: − 1 𝜅𝜅𝑇𝑇 𝑣𝑣 = − 𝑅𝑅𝑅𝑅(𝑣𝑣 + 2𝑏𝑏) 𝑣𝑣3 = 𝑇𝑇𝑇𝑇′(𝑣𝑣) ⟹ 𝑔𝑔′(𝑣𝑣) = − 𝑅𝑅(𝑣𝑣 + 2𝑏𝑏) 𝑣𝑣3 Determinamos 𝑔𝑔(𝑣𝑣): 𝑔𝑔(𝑣𝑣) = −𝑅𝑅 � 𝑣𝑣 + 2𝑏𝑏 𝑣𝑣3 𝑑𝑑𝑑𝑑 = 𝑅𝑅 � 1 𝑣𝑣 + 𝑏𝑏 𝑣𝑣2 � + 𝐶𝐶 Así, la ecuación térmica de estado queda: 𝑝𝑝 = 𝑅𝑅𝑅𝑅 � 1 𝑣𝑣 + 𝑏𝑏 𝑣𝑣2 � + 𝐶𝐶 Para valores grandes del volumen molar, el comportamiento del gas tiende al ideal. Esta información nos permite hallar 𝐶𝐶. En efecto: 𝑣𝑣 grande ⟹ 1 𝑣𝑣2 ≪ 1 𝑣𝑣 ⟹ 𝑝𝑝 ≅ 𝑅𝑅𝑅𝑅 𝑣𝑣 + 𝐶𝐶 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 9. Que resulta ser la ecuación térmica del gas ideal si 𝐶𝐶 = 0. Finalmente: 𝑝𝑝 = 𝑅𝑅𝑅𝑅 � 1 𝑣𝑣 + 𝑏𝑏 𝑣𝑣2 � b) La expresión del coeficiente de dilatación cúbica la determinamos a través de la relación: 𝛼𝛼 = 𝑝𝑝𝜅𝜅𝑇𝑇 𝛽𝛽 = 𝑝𝑝𝑝𝑝2 𝑅𝑅𝑇𝑇 2(𝑣𝑣 + 2𝑏𝑏) Conocemos temperatura y volumen molar, pero no la presión. La calculamos a partir de la ecuación térmica: 𝑝𝑝 = 0.082 atmL Kmol ⋅ 300 K ⋅ � 1 1 L mol⁄ + 0.04 L mol⁄ 1 L2 mol2⁄ � = 25.6 atm Sustituyendo: 𝛼𝛼 = (25.6 atm)(1 L mol⁄ )2 �0.082 atmL Kmol� ⋅ (300 K)2 ⋅ (1 L mol⁄ + 2 ⋅ 0.04 L mol⁄ ) = 3.21 ⋅ 10−3 K−1 8.- Obtener la ecuación para una transformación adiabática reversible de un sistema para el cual la energía interna molar es de la forma 𝑢𝑢 = 𝑎𝑎𝑎𝑎𝑎𝑎 + 𝑏𝑏, con 𝑎𝑎,𝑏𝑏 constantes. El primer principio de la Termodinámica postula que: d𝑈𝑈 = 𝛿𝛿𝛿𝛿 − 𝛿𝛿𝛿𝛿 = 𝛿𝛿𝛿𝛿 − 𝑝𝑝d𝑉𝑉 En una transformación adiabática, 𝛿𝛿𝛿𝛿 = 0: d𝑈𝑈 = −𝑝𝑝d𝑉𝑉 O bien, en función de magnitudes molares: 𝑛𝑛d𝑢𝑢 = −𝑛𝑛𝑛𝑛d𝑣𝑣 ⟹ d𝑢𝑢 = −𝑝𝑝d𝑣𝑣 En este caso: 𝑢𝑢 = 𝑎𝑎𝑎𝑎𝑎𝑎 + 𝑏𝑏 ⟹ d𝑢𝑢 = 𝑎𝑎d(𝑝𝑝𝑝𝑝) = 𝑎𝑎𝑎𝑎d𝑣𝑣 + 𝑎𝑎𝑎𝑎d𝑝𝑝 Se trata, por consiguiente, de resolver la ecuación diferencial: 𝑎𝑎𝑎𝑎d𝑣𝑣 + 𝑎𝑎𝑎𝑎d𝑝𝑝 = −𝑝𝑝d𝑣𝑣 ⟹ 𝑝𝑝(𝑎𝑎 + 1)d𝑣𝑣 + 𝑎𝑎𝑎𝑎d𝑝𝑝 = 0 ⟹ (𝑎𝑎 + 1) d𝑣𝑣 𝑣𝑣 + 𝑎𝑎 d𝑝𝑝 𝑝𝑝 = 0 Integrando: (𝑎𝑎 + 1) ln 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑎𝑎 ln 𝑝𝑝𝑖𝑖 𝑝𝑝𝑓𝑓 ⟹ � 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 � 𝑎𝑎+1 𝑎𝑎 = 𝑝𝑝𝑖𝑖 𝑝𝑝𝑓𝑓 ⟹ 𝑝𝑝𝑖𝑖 𝑣𝑣𝑖𝑖 𝑎𝑎+1 𝑎𝑎 = 𝑝𝑝𝑖𝑖 𝑣𝑣𝑓𝑓 𝑎𝑎+1 𝑎𝑎 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 10. 9.- El calor específico a presión constante de un gas ideal es 𝑐𝑐𝑝𝑝(J mol ⋅ K⁄ ) = 5𝑅𝑅 2 + 𝐴𝐴𝐴𝐴⁄ siendo 𝐴𝐴 una constante. Determinar la ecuación de las adiabáticas de este sistema. El planteamiento es análogo al del ejercicio anterior. Partimos de: d𝑢𝑢 = −𝑝𝑝d𝑣𝑣 Como el sistema considerado es un gas ideal, su energía interna es de la forma: d𝑢𝑢 = 𝑐𝑐𝑣𝑣d𝑇𝑇 = �𝑐𝑐𝑝𝑝 − 𝑅𝑅�d𝑇𝑇 = � 3 2 𝑅𝑅 + 𝐴𝐴𝐴𝐴� d𝑇𝑇 Aplicando el primer principio: � 3 2 𝑅𝑅 + 𝐴𝐴𝐴𝐴 � d𝑇𝑇 = −𝑝𝑝d𝑣𝑣 = − 𝑅𝑅𝑅𝑅 𝑣𝑣 d𝑣𝑣 ⟹ � 3𝑅𝑅 2 1 𝑇𝑇 + 𝐴𝐴� d𝑇𝑇 = −𝑅𝑅 d𝑣𝑣 𝑣𝑣 Queda: 3𝑅𝑅 2 ln 𝑇𝑇 + 𝐴𝐴𝐴𝐴 = −𝑅𝑅 ln 𝑣𝑣 + 𝐶𝐶 ⟹ ln �𝑇𝑇 3 2 𝑣𝑣� + 𝐴𝐴 𝑅𝑅 𝑇𝑇 = cte 10.- Determinar el rendimiento de un ciclo de Carnot recorrido por un gas de van der Waals, conocidas sus ecuaciones térmica y energética. Comenzamos determinando los calores transferidos entre el gas de van der Waals y los focos en los dos procesos isotermos. Para ello, recurrimos al primer principio de la Termodinámica y despejamos el calor: ∆𝑈𝑈 = 𝑄𝑄 − 𝑊𝑊 ⟹ 𝑄𝑄 = ∆𝑈𝑈 + 𝑊𝑊 Hallamos el trabajo efectuado en el proceso isotermo (reversible): 𝑊𝑊 = 𝑛𝑛� 𝑝𝑝𝑒𝑒𝑒𝑒𝑒𝑒 𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 =⏞ 𝑝𝑝𝑒𝑒𝑒𝑒𝑒𝑒=𝑝𝑝= 𝑅𝑅𝑅𝑅 𝑣𝑣−𝑏𝑏− 𝑎𝑎 𝑣𝑣2 𝑛𝑛 � � 𝑅𝑅𝑅𝑅 𝑣𝑣 − 𝑏𝑏 − 𝑎𝑎 𝑣𝑣2 � 𝑑𝑑𝑑𝑑 𝑣𝑣𝑓𝑓 𝑣𝑣𝑖𝑖 = 𝑛𝑛�𝑅𝑅𝑅𝑅 ln(𝑣𝑣 − 𝑏𝑏) + 𝑎𝑎 𝑣𝑣 � 𝑣𝑣𝑖𝑖 𝑣𝑣𝑓𝑓 Así: 𝑊𝑊 = 𝑛𝑛�𝑅𝑅𝑅𝑅 ln 𝑣𝑣𝑓𝑓 − 𝑏𝑏 𝑣𝑣𝑖𝑖 − 𝑏𝑏 + 𝑎𝑎 � 1 𝑣𝑣𝑓𝑓 − 1 𝑣𝑣𝑖𝑖 �� Por otra parte, la variación de energía interna es: ∆𝑈𝑈 = 𝑛𝑛�𝑐𝑐(𝑇𝑇2 − 𝑇𝑇1) − 𝑎𝑎 � 1 𝑣𝑣𝑓𝑓 − 1 𝑣𝑣𝑖𝑖 �� =⏞ 𝑇𝑇1=𝑇𝑇2 − 𝑛𝑛𝑛𝑛 � 1 𝑣𝑣𝑓𝑓 − 1 𝑣𝑣𝑖𝑖 � El calor queda: 𝑄𝑄 = 𝑛𝑛𝑛𝑛𝑛𝑛 ln 𝑣𝑣𝑓𝑓 − 𝑏𝑏 𝑣𝑣𝑖𝑖 − 𝑏𝑏 A continuación, buscaremos una relación entre los volúmenes finales e iniciales en las transformaciones adiabáticas, en las que se verifica 𝑄𝑄 = 0: d𝑈𝑈 = −𝛿𝛿𝛿𝛿 ⟹ 𝑐𝑐d𝑇𝑇 + 𝑎𝑎 𝑣𝑣2 d𝑣𝑣 = −𝑝𝑝d𝑣𝑣 = − � 𝑅𝑅𝑅𝑅 𝑣𝑣 − 𝑏𝑏 − 𝑎𝑎 𝑣𝑣2 � d𝑣𝑣 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 11. Resolvemos la ecuación diferencial resultante: 𝑐𝑐d𝑇𝑇 = − 𝑅𝑅𝑅𝑅 𝑣𝑣 − 𝑏𝑏 d𝑣𝑣 ⟹ d𝑇𝑇 𝑇𝑇 = − 𝑅𝑅𝑅𝑅 𝑐𝑐(𝑣𝑣 − 𝑏𝑏) d𝑣𝑣 ⟹ ln 𝑇𝑇 = − 𝑅𝑅𝑅𝑅 𝑐𝑐 ln(𝑣𝑣 − 𝑏𝑏) + 𝐶𝐶 La relación entre los volúmenes final e inicial es, de esta forma: 𝑇𝑇 (𝑣𝑣 − 𝑏𝑏) 𝑅𝑅𝑅𝑅 𝑐𝑐 = 𝑐𝑐𝑐𝑐𝑐𝑐.⟹ 𝑣𝑣2 − 𝑏𝑏 𝑣𝑣1 − 𝑏𝑏 = 𝑣𝑣3 − 𝑏𝑏 𝑣𝑣4 − 𝑏𝑏 Conocido todo lo anterior, podemos proceder a obtener el rendimiento de la máquina térmica: 𝜂𝜂 = 1 + 𝑄𝑄2 𝑄𝑄1 = 1 + 𝑛𝑛𝑛𝑛𝑇𝑇2 ln 𝑣𝑣4 − 𝑏𝑏 𝑣𝑣3 − 𝑏𝑏 𝑛𝑛𝑛𝑛𝑇𝑇1 ln 𝑣𝑣2 − 𝑏𝑏 𝑣𝑣1 − 𝑏𝑏 = 1 − 𝑛𝑛𝑛𝑛𝑇𝑇2 ln 𝑣𝑣3 − 𝑏𝑏 𝑣𝑣4 − 𝑏𝑏 𝑛𝑛𝑛𝑛𝑇𝑇1 ln 𝑣𝑣2 − 𝑏𝑏 𝑣𝑣1 − 𝑏𝑏 =⏞ 𝑣𝑣2−𝑏𝑏 𝑣𝑣1−𝑏𝑏= 𝑣𝑣3−𝑏𝑏 𝑣𝑣4−𝑏𝑏 1 − 𝑇𝑇2 𝑇𝑇1 11.- Un calorímetro de aluminio de 200 g contiene 500 g de agua a 20 ºC. Dentro del recipiente se introduce un trozo de hielo de 100 g enfriado a -20 ºC. (a) Calcular la temperatura final del sistema, suponiendo que no hay pérdidas de calor. (b) Se añade un segundo trozo de hielo de 200 g a -20 ºC. ¿Cuál será la temperatura y composición final del sistema una vez que se ha alcanzado el equilibrio? a) Inicialmente, el calorímetro contiene cinco veces más agua que hielo. Considerando además que la diferencia entre las temperaturas iniciales de ambas sustancias y la temperatura de fusión del hielo es la misma y que el calor latente de fusión del agua es relativamente pequeño, parece sensato suponer que, en el equilibrio, todo el hielo se habrá fundido. Los calores transferidos en base a esta hipótesis son: 𝑄𝑄AGUA = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎�𝑇𝑇𝑓𝑓 − 𝑇𝑇𝑎𝑎� 𝑄𝑄HIELO = 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎�𝑇𝑇𝑓𝑓 − 𝑇𝑇fusión� 𝑄𝑄CALORÍMETRO = 𝑚𝑚 𝐴𝐴𝑙𝑙 𝑐𝑐𝐴𝐴𝐴𝐴(𝑇𝑇f − 𝑇𝑇𝑎𝑎) El interior del calorímetro se halla térmicamente aislado respecto del exterior, lo que implica que ∑ 𝑄𝑄𝑖𝑖 = 𝑄𝑄AGUA + 𝑄𝑄HIELO + 𝑄𝑄CALORÍMETRO = 0. Despejamos la temperatura final en esta última igualdad: 𝑇𝑇𝑓𝑓 = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎 𝑇𝑇𝑎𝑎 − 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) − 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎 𝑇𝑇fusión + 𝑚𝑚𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴 𝑇𝑇𝑎𝑎 𝑐𝑐𝑎𝑎(𝑚𝑚𝑎𝑎 + 𝑚𝑚ℎ) + 𝑚𝑚𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴 Sustituyendo 𝑚𝑚𝑎𝑎 = 500 g, 𝑚𝑚ℎ = 100 g, 𝑚𝑚 𝐴𝐴𝐴𝐴 = 200 g, 𝑐𝑐𝑎𝑎 = 1 cal g ⋅ C∘ ⁄ , 𝑐𝑐ℎ = 0.6 cal g ⋅ C∘ ⁄ , 𝑐𝑐𝐴𝐴𝐴𝐴 = 0.216 cal g ⋅ C∘ ⁄ (1 J = 0.24 cal), 𝑇𝑇𝑎𝑎 = 20 C∘ , 𝑇𝑇ℎ = −20 C∘ , 𝑇𝑇fusión = 0 C∘ , 𝐿𝐿𝑓𝑓 = 80 cal g⁄ resulta 𝑇𝑇𝑓𝑓 = 2.6 C∘ , que verifica 𝑇𝑇fusión < 𝑇𝑇𝑓𝑓 < 𝑇𝑇𝑎𝑎 y, por tanto, concuerda con la hipótesis de partida. b) Nuevamente, la mezcla inicial está constituida fundamentalmente por agua, pero esta y el calorímetro se encuentran ahora a una temperatura mucho más próxima al punto de fusión que el hielo. Como primera hipótesis, supondremos que la temperatura final del sistema será 0 C∘ , pero que no todo el hielo se habrá fundido. Nuestra incógnita será, por tanto, la masa de hielo que se ha transformado en agua. Planteamos los calores: 𝑄𝑄AGUA = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) 𝑄𝑄HIELO = 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚′ℎ 𝐿𝐿𝑓𝑓 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 12. 𝑄𝑄CALORÍMETRO = 𝑚𝑚 𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) Combinando estas expresiones con ∑ 𝑄𝑄𝑖𝑖 = 0 deducimos que: 𝑚𝑚′ℎ = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎(𝑇𝑇𝑎𝑎 − 𝑇𝑇fusión) + 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇ℎ − 𝑇𝑇fusión) + 𝑚𝑚𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴(𝑇𝑇𝑎𝑎 − 𝑇𝑇fusión) 𝐿𝐿𝑓𝑓 Tomando 𝑚𝑚𝑎𝑎 = 600 g, 𝑚𝑚ℎ = 200 g, 𝑚𝑚 𝐴𝐴𝐴𝐴 = 200 g, 𝑇𝑇𝑎𝑎 = 2.6 C∘ , 𝑇𝑇ℎ = −20 C∘ , 𝑇𝑇fusión = 0 C∘ se obtiene 𝑚𝑚′ℎ = −9.1 g, lo cual carece de sentido, así que descartamos la hipótesis inicial. En su lugar, postulamos que cierta cantidad agua pasa a estado sólido antes de llegar al equilibrio. Los calores quedan: 𝑄𝑄AGUA = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) − 𝑚𝑚′𝑎𝑎 𝐿𝐿𝑓𝑓 𝑄𝑄HIELO = 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) 𝑄𝑄CALORÍMETRO = 𝑚𝑚 𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) Determinamos 𝑚𝑚′𝑎𝑎: 𝑚𝑚′𝑎𝑎 = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) + 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚𝐴𝐴𝐴𝐴 𝑐𝑐𝐴𝐴𝐴𝐴(𝑇𝑇fusión − 𝑇𝑇𝑎𝑎) 𝐿𝐿𝑓𝑓 = 9.1 g Vemos que 0 < 𝑚𝑚′𝑎𝑎 < 𝑚𝑚𝑎𝑎, como se esperaba. Así, en el equilibrio, la mezcla, compuesta por 590.9 g de agua y 209.1 g de hielo, está a una temperatura de 0 C∘ . 12.- Calcular la temperatura de equilibrio cuando en un recipiente aislado se introducen las siguientes sustancias: - 48 g de hielo a -40 ºC. - 91 g de agua líquida a 22 ºC. - 25 g de vapor de agua a 200 ºC. El calor latente de vaporización del agua es muy elevado en comparación con el resto de parámetros involucrados. Podemos, pues, conjeturar que, en el equilibrio, la mezcla contendrá solo agua y vapor, donde parte del vapor de agua que había en un principio se ha condensado. Escribimos los calores (en este ejercicio se desprecia la participación del calorímetro): 𝑄𝑄AGUA = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎�𝑇𝑇vap − 𝑇𝑇𝑎𝑎� 𝑄𝑄HIELO = 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎�𝑇𝑇vap − 𝑇𝑇fusión� 𝑄𝑄VAPOR = 𝑚𝑚𝑣𝑣 𝑐𝑐𝑣𝑣�𝑇𝑇vap − 𝑇𝑇𝑣𝑣� − 𝑚𝑚′𝑣𝑣 𝐿𝐿𝑣𝑣 Aplicando ∑ 𝑄𝑄𝑖𝑖 = 0 se llega a: 𝑚𝑚′𝑣𝑣 == 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎�𝑇𝑇vap − 𝑇𝑇𝑎𝑎� + 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎�𝑇𝑇vap − 𝑇𝑇fusión� + 𝑚𝑚𝑣𝑣 𝑐𝑐𝑣𝑣�𝑇𝑇vap − 𝑇𝑇𝑣𝑣� 𝐿𝐿𝑣𝑣 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 13. Tomando 𝑚𝑚𝑎𝑎 = 91 g, 𝑚𝑚ℎ = 48 g, 𝑚𝑚𝑣𝑣 = 25 g, 𝑐𝑐𝑣𝑣 = 0.5 cal g ⋅ C∘ ⁄ ,𝑇𝑇𝑎𝑎 = 22 C∘ , 𝑇𝑇ℎ = −40 C∘ , 𝑇𝑇𝑣𝑣 = 200 C∘ 𝑇𝑇fusión = 0 C∘ , 𝑇𝑇vap = 100 C∘ , 𝐿𝐿𝑣𝑣 = 540 cal g⁄ se obtiene 𝑚𝑚′𝑣𝑣 = 29.0 g, que es mayor que la masa inicial de vapor. Nos damos cuenta de que el calor puesto en juego no solo supone la condensación de todo el vapor sino que, además, comporta que la temperatura final del sistema sea menor que 𝑇𝑇vap. En virtud de esta segunda suposición, los calores valen: 𝑄𝑄AGUA = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎�𝑇𝑇𝑓𝑓 − 𝑇𝑇𝑎𝑎� 𝑄𝑄HIELO = 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) + 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎�𝑇𝑇𝑓𝑓 − 𝑇𝑇fusión� 𝑄𝑄VAPOR = 𝑚𝑚𝑣𝑣 𝑐𝑐𝑣𝑣�𝑇𝑇vap − 𝑇𝑇𝑣𝑣� − 𝑚𝑚𝑣𝑣 𝐿𝐿𝑣𝑣 + 𝑚𝑚𝑣𝑣 𝑐𝑐𝑎𝑎�𝑇𝑇𝑓𝑓 − 𝑇𝑇vap� De esta forma, 𝑇𝑇𝑓𝑓 es: 𝑇𝑇𝑓𝑓 = 𝑚𝑚𝑎𝑎 𝑐𝑐𝑎𝑎 𝑇𝑇𝑎𝑎 − 𝑚𝑚ℎ 𝑐𝑐ℎ(𝑇𝑇fusión − 𝑇𝑇ℎ) − 𝑚𝑚ℎ 𝐿𝐿𝑓𝑓 + 𝑚𝑚ℎ 𝑐𝑐𝑎𝑎 𝑇𝑇fusión − 𝑚𝑚𝑣𝑣 𝑐𝑐𝑣𝑣�𝑇𝑇vap − 𝑇𝑇𝑣𝑣� + 𝑚𝑚𝑣𝑣 𝐿𝐿𝑣𝑣 + 𝑚𝑚𝑣𝑣 𝑐𝑐𝑎𝑎 𝑇𝑇vap 𝑐𝑐𝑎𝑎(𝑚𝑚𝑎𝑎 + 𝑚𝑚ℎ + 𝑚𝑚𝑣𝑣) Sustituyendo, 𝑇𝑇𝑓𝑓 = 87.0 C∘ . Este resultado es válido, ya que 𝑇𝑇𝑎𝑎 < 𝑇𝑇𝑓𝑓 < 𝑇𝑇vap. En el equilibrio, la mezcla, formada por 164 g de agua, está a 87.0 C∘ . 13.- Un sistema tiene una capacidad calorífica dada por 𝐶𝐶 = 𝐴𝐴𝑇𝑇 2 donde 𝐴𝐴 es una constante cuyo valor es 𝐴𝐴 = 0.01 cal K3 ⁄ . El sistema se encuentra inicialmente a la temperatura de 200 K y se dispone de un foco térmico a 100 K. Calcular: (a) La cantidad máxima de trabajo que se puede obtener cuando se enfría el sistema hasta la temperatura del foco. (b) El rendimiento de esta operación. a) Situamos una máquina térmica entre los dos sistemas para así obtener trabajo a partir del intercambio de calor entre los mismos. La máquina ha de operar reversiblemente para que produzca la mayor cantidad de trabajo posible (ya que son las máquinas térmicas reversibles las que gozan de un mayor rendimiento). Se sabe que el funcionamiento de la máquina cesará cuando el sistema a 𝑇𝑇𝑖𝑖 = 200 K alcance la temperatura de equilibrio 𝑇𝑇𝑓𝑓 = 100 K. Necesitamos disponer del calor absorbido por el foco frío, que determinamos a partir de la variación de entropía del universo, nula por tratarse de una máquina reversible: ∆𝑆𝑆UNIVERSO = ∆𝑆𝑆SISTEMA + ∆𝑆𝑆FOCO = 0 La transferencia de calor del sistema a la máquina es un proceso irreversible. Un proceso reversible con los mismos estados inicial y final requeriría de infinitos focos, es decir: ∆𝑆𝑆SISTEMA = � 𝛿𝛿𝛿𝛿 𝑇𝑇𝑅𝑅 = � 𝛿𝛿𝛿𝛿 𝑇𝑇 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 = � 𝐶𝐶d𝑇𝑇 𝑇𝑇 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 = � 𝐴𝐴𝐴𝐴d𝑇𝑇 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 = 𝐴𝐴 2 �𝑇𝑇𝑓𝑓 2 − 𝑇𝑇𝑖𝑖 2 � La variación de entropía del foco es inmediata: ∆𝑆𝑆FOCO = 𝑄𝑄2 𝑇𝑇𝑓𝑓 De esta forma: 𝐴𝐴 2 �𝑇𝑇𝑓𝑓 2 − 𝑇𝑇𝑖𝑖 2 � + 𝑄𝑄 𝑇𝑇𝑓𝑓 = 0 ⟹ 𝑄𝑄 = 𝐴𝐴 2 𝑇𝑇𝑓𝑓�𝑇𝑇𝑖𝑖 2 − 𝑇𝑇𝑓𝑓 2 � MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 14. Sustituyendo: 𝑄𝑄2 = 1 2 ⋅ 0.01 cal K3 ⁄ ⋅ 100 K ⋅ [(200 K)2 − (100 K)2 ] = 15 kcal El calor cedido por el sistema viene dado por: 𝛿𝛿𝑄𝑄1 = 𝐶𝐶d𝑇𝑇 = 𝐴𝐴𝑇𝑇 2 d𝑇𝑇 ⟹ 𝑄𝑄1 = � 𝐴𝐴𝑇𝑇 2 d𝑇𝑇 = 𝐴𝐴 3 �𝑇𝑇𝑓𝑓 3 − 𝑇𝑇𝑖𝑖 2 � 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 Numéricamente: 𝑄𝑄1 = 1 3 ⋅ 0.01 cal K3 ⁄ ⋅ [(100 K)3 − (200 K)3 ] = −23.3 kcal El trabajo devuelto por la máquina térmica se calcula como la suma de estos calores, asignándole los signos que se corresponden con el punto de vista de la máquina: 𝑊𝑊 = |𝑄𝑄1| − |𝑄𝑄2| = 23.3 kcal − 15 kcal = 8.3 kcal b) Aplicamos la definición de rendimiento: 𝜂𝜂 = 𝑊𝑊 𝑄𝑄ABSORBIDO = 8.3 23.3 = 0.36 14.- Un gas ideal monoatómico (𝑐𝑐𝑣𝑣 = 3 2 𝑅𝑅) ocupa inicialmente (A) un volumen de 5 litros y está a la temperatura de 200 K. Se calienta de forma reversible e isócora (B) hasta alcanzar una presión de 8 atm. A continuación se expande reversible e isotérmicamente (C) hasta duplicar su volumen. Mediante una expansión adiabática brusca (D) contra una presión exterior constante de 2 atm se lleva el gas hasta un estado tal que cuando se comprime de forma isóbara y reversible se vuelve al estado inicial (A), recorriendo así un ciclo. Calcular: (a) las variables termodinámicas de cada uno de los estados intermedios del ciclo. (b) La variación de entropía del gas y del universo durante el ciclo. (c) El rendimiento del ciclo. a) Determinamos las variables termodinámicas en las distintas etapas: (A) Me es imposible, en principio, hallar la presión del gas, pues desconocemos el número de moles. Avanzando en el enunciado del problema, descubro que cuando el gas se expande contra una presión constante de 2 atm y más tarde se efectúa una transformación isóbara, este vuelve al estado inicial. En consecuencia, la presión inicial del gas es 𝑝𝑝𝐴𝐴 = 2 atm. Obtengo el número de moles: 𝑛𝑛 = 𝑝𝑝𝐴𝐴 𝑉𝑉𝐴𝐴 𝑅𝑅𝑇𝑇𝐴𝐴 = (2 atm) ⋅ (5 L) �0.082 atm ⋅ L K ⋅ mol� ⋅ (200 K) = 0.61 mol (B) El gas se somete a un proceso isócoro, así que el volumen permanece constante: 𝑉𝑉 𝐵𝐵 = 5 L. Conocida la presión, despejamos la temperatura de la ecuación de estado: 𝑇𝑇𝐵𝐵 = 𝑝𝑝𝐴𝐴 𝑉𝑉𝐴𝐴 𝑛𝑛𝑛𝑛 = (8 atm) ⋅ (5 L) �0.082 atm ⋅ L K ⋅ mol� ⋅ (0.61 mol) = 800 K (C) En este caso, el proceso es isotermo: 𝑇𝑇𝐶𝐶 = 800 K. Conozco asimismo el volumen final: 𝑉𝑉𝐶𝐶 = 2𝑉𝑉 𝐵𝐵 = 10 L. Finalmente, la presión es: 𝑝𝑝𝐶𝐶 = 𝑛𝑛𝑛𝑛𝑇𝑇𝐶𝐶 𝑉𝑉𝐶𝐶 = �0.082 atm ⋅ L K ⋅ mol � ⋅ (0.61 mol) ⋅ (800 K) (10 L) = 4 atm MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 15. (D) Solo dispongo de la presión final, 𝑝𝑝 𝐷𝐷 = 2 atm. Como el proceso es adiabático: ∆𝑈𝑈 = −𝑊𝑊 O bien: 𝑛𝑛𝑐𝑐𝑣𝑣(𝑇𝑇 𝐷𝐷 − 𝑇𝑇𝐶𝐶) = −𝑝𝑝 𝐷𝐷(𝑉𝑉 𝐷𝐷 − 𝑉𝑉𝐶𝐶) La ecuación de estado hace posible expresar 𝑉𝑉 𝐷𝐷 en función del resto de variables termodinámicas: 𝑉𝑉 𝐷𝐷 = 𝑛𝑛𝑛𝑛𝑇𝑇 𝐷𝐷 𝑝𝑝 𝐷𝐷 ⟹ 𝑛𝑛𝑐𝑐𝑣𝑣(𝑇𝑇 𝐷𝐷 − 𝑇𝑇𝐶𝐶) = −𝑝𝑝 𝐷𝐷 � 𝑛𝑛𝑛𝑛𝑇𝑇 𝐷𝐷 𝑝𝑝 𝐷𝐷 − 𝑉𝑉𝐶𝐶� Despejamos 𝑇𝑇 𝐷𝐷: 𝑛𝑛𝑐𝑐𝑣𝑣 𝑇𝑇 𝐷𝐷 − 𝑛𝑛𝑐𝑐𝑣𝑣 𝑇𝑇𝐶𝐶 = 𝑝𝑝 𝐷𝐷 𝑉𝑉𝐶𝐶 − 𝑛𝑛𝑛𝑛𝑇𝑇 𝐷𝐷 ⟹ 𝑇𝑇 𝐷𝐷 = 𝑝𝑝 𝐷𝐷 𝑉𝑉𝐶𝐶 + 𝑛𝑛𝑐𝑐𝑣𝑣 𝑇𝑇𝐶𝐶 𝑛𝑛(𝑐𝑐𝑣𝑣 + 𝑅𝑅) Cuyo valor es: 𝑇𝑇 𝐷𝐷 = (2 atm) ⋅ (10 L) + (0.61 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol� ⋅ (800 K) (0.61 mol) ⋅ 5 2 ⋅ �0.082 atm ⋅ L K ⋅ mol� = 640 K Y el volumen: 𝑉𝑉 𝐷𝐷 = (0.61 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (640 K) (2 atm) = 16 L 𝐀𝐀 𝐁𝐁 𝐂𝐂 𝐃𝐃 𝑽𝑽 (L) 𝟓𝟓 𝟓𝟓 𝟏𝟏𝟏𝟏 𝟏𝟏𝟏𝟏 𝒑𝒑 (atm) 𝟐𝟐 𝟖𝟖 𝟒𝟒 𝟐𝟐 𝑻𝑻 (K) 𝟐𝟐𝟐𝟐𝟐𝟐 𝟖𝟖𝟖𝟖𝟖𝟖 𝟖𝟖𝟖𝟖𝟖𝟖 𝟔𝟔𝟔𝟔𝟔𝟔 b) La entropía es función de estado: ∆𝑆𝑆GAS = 0 Por otra parte, solo aquellos procesos que sean irreversibles contribuyen a incrementar la entropía del universo. En nuestro ciclo, el único proceso irreversible es el CD. Como el proceso es adiabático, el gas se halla térmicamente aislado y no intercambia calor con los focos, así que la entropía de los segundos permanece constante: ∆𝑆𝑆UNIVERSO = ∆𝑆𝑆GAS,CD = 𝑛𝑛𝑐𝑐𝑣𝑣 ln 𝑇𝑇 𝐷𝐷 𝑇𝑇𝐶𝐶 + 𝑛𝑛𝑛𝑛 ln 𝑉𝑉 𝐷𝐷 𝑉𝑉𝐶𝐶 De esta forma: ∆𝑆𝑆UNIVERSO = (0.61 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ ln 640 800 + (0.61 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ ln 16 10 = 6.77 ⋅ 10−3 cal K c) Empecemos calculando el trabajo total efectuado en un ciclo: El proceso AB es isócoro (d𝑉𝑉 = 0). Por tanto, 𝑊𝑊 𝐴𝐴𝐴𝐴 = 0. MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 16. El proceso BC es una expansión isoterma reversible: 𝑊𝑊 𝐵𝐵𝐵𝐵 = 𝑛𝑛𝑛𝑛𝑇𝑇𝐵𝐵 ln 2𝑉𝑉 𝐵𝐵 𝑉𝑉 𝐵𝐵 = (0.61 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (800 K) ⋅ ln 2 = 27.7 atm ⋅ L El proceso CD es una expansión frente a una presión exterior constante: 𝑊𝑊𝐶𝐶𝐶𝐶 = 𝑝𝑝 𝐷𝐷(𝑉𝑉 𝐷𝐷 − 𝑉𝑉𝐶𝐶) = (2 atm) ⋅ (6 L) = 12 atm ⋅ L El proceso DA es una compresión isóbara reversible: 𝑊𝑊 𝐷𝐷𝐷𝐷 = 𝑝𝑝 𝐷𝐷(𝑉𝑉𝐴𝐴 − 𝑉𝑉 𝐷𝐷) = −(2 atm) ⋅ (9 L) = −18 atm ⋅ L En suma: 𝑊𝑊𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 = 21.7 atm ⋅ L A continuación, obtenemos el calor intercambiado por el sistema en cada proceso a partir del primer principio, ∆𝑈𝑈 = 𝑄𝑄 − 𝑊𝑊 ⟹ 𝑄𝑄 = ∆𝑈𝑈 + 𝑊𝑊 = 𝑛𝑛𝑐𝑐𝑣𝑣∆𝑇𝑇 + 𝑊𝑊: 𝑄𝑄𝐴𝐴𝐴𝐴 = (0.61 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (600 K) = 45 atm ⋅ L 𝑄𝑄𝐵𝐵𝐵𝐵 = 𝑊𝑊 𝐵𝐵𝐵𝐵 = 27.7 atm ⋅ L 𝑄𝑄𝐶𝐶𝐶𝐶 = 0 (proceso adiabático) 𝑄𝑄 𝐷𝐷𝐷𝐷 = −(0.61 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (440 K) − 18 atm ⋅ L = −51 atm ⋅ L El calor absorbido a lo largo de un ciclo es: 𝑄𝑄ABSORBIDO = 𝑄𝑄𝐴𝐴𝐴𝐴 + 𝑄𝑄𝐵𝐵𝐵𝐵 = 72.7 atm ⋅ L Y el rendimiento: 𝜂𝜂 = 𝑊𝑊 𝑄𝑄ABSORBIDO = 21.7 72.7 = 0.30 15.- Un cilindro de paredes aislantes está provisto de un émbolo aislante sin rozamiento que lo separa en dos zonas A y B. En cada zona hay 8 moles de un gas ideal para el que 𝛾𝛾 = 1.4, que se encuentran ambos a 20 ºC y 1 atm de presión. Mediante una resistencia eléctrica se proporciona una cantidad de trabajo eléctrico 𝑊𝑊𝑒𝑒 al gas de A, que se expansiona y comprime al que hay en B, hasta que la presión es de 3 atm. Calcular: (a) el trabajo efectuado por el émbolo. (b) Las temperaturas finales en A y B. (c) El trabajo eléctrico 𝑊𝑊𝑒𝑒 suministrado. (d) la variación de entropía de ambos gases. a) Es claro que el proceso que experimenta el gas en B es adiabático. Asumiremos asimismo que es cuasiestático, aunque no se indique de forma explícita en el enunciado. Podemos, en tal caso, aplicar la ecuación de las adiabáticas para calcular el volumen final del gas. Antes, necesitamos conocer el volumen inicial, para lo cual recurrimos a la ecuación de estado: 𝑉𝑉 𝐵𝐵𝐵𝐵 = 𝑛𝑛𝑛𝑛𝑇𝑇𝐵𝐵𝐵𝐵 𝑝𝑝𝐵𝐵𝐵𝐵 = (8 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (293 K) (1 atm) = 192.2 L Estamos en condiciones de hacer uso de la ecuación de las adiabáticas para un gas ideal: 𝑝𝑝𝐵𝐵𝐵𝐵 𝑉𝑉 𝐵𝐵𝐵𝐵 𝛾𝛾 = 𝑝𝑝𝐵𝐵𝐵𝐵 𝑉𝑉 𝐵𝐵𝐵𝐵 𝛾𝛾 ⟹ 𝑉𝑉𝐵𝐵𝐵𝐵 = � 𝑝𝑝𝐵𝐵𝐵𝐵 𝑝𝑝𝐵𝐵𝐵𝐵 � 1 𝛾𝛾 𝑉𝑉 𝐵𝐵𝐵𝐵 = � 1 3 � 1 1.4 ⋅ 192.2 L = 87.7 L MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 17. El trabajo sobre el gas viene dado por: 𝑊𝑊 𝐵𝐵 = 𝑝𝑝𝐵𝐵𝐵𝐵 𝑉𝑉 𝐵𝐵𝐵𝐵 − 𝑝𝑝𝐵𝐵𝐵𝐵 𝑉𝑉 𝐵𝐵𝐵𝐵 𝛾𝛾 − 1 = (1 atm) ⋅ (192.2 L) − (3 atm) ⋅ (87.7 L) 1.4 − 1 = −177.3 atm ⋅ L Sin embargo, el émbolo está realizando trabajo sobre otro sistema: 𝑊𝑊ÉMBOLO = 177.3 atm ⋅ L. b) Encontramos la temperatura final en B a través de la ecuación de estado: 𝑇𝑇𝐵𝐵𝐵𝐵 = 𝑝𝑝𝐵𝐵𝐵𝐵 𝑉𝑉 𝐵𝐵𝐵𝐵 𝑛𝑛𝑛𝑛 = (3 atm) ⋅ (87.7 L) (8 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol� = 401.1 K El volumen final en A no es sino la diferencia entre el volumen final en B y el volumen total, que es constante: 𝑉𝑉𝐴𝐴𝐴𝐴 = 2 ⋅ 192.2 atm ⋅ L − 87.7 atm ⋅ L = 296.7 atm ⋅ L. De nuevo, usamos la ecuación de los gases ideales para obtener la temperatura restante: 𝑇𝑇𝐴𝐴𝐴𝐴 = 𝑝𝑝𝐴𝐴𝐴𝐴 𝑉𝑉𝐴𝐴𝐴𝐴 𝑛𝑛𝑛𝑛 = (3 atm) ⋅ (296.7 L) (8 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol� = 1356.9 K c) En virtud del primer principio, escribimos: ∆𝑈𝑈𝐴𝐴 + ∆𝑈𝑈𝐵𝐵 = −𝑊𝑊𝑒𝑒 Ya que la única transferencia de energía entre el sistema compuesto por los dos gases y el medio externo es la que se corresponde con el trabajo eléctrico de la resistencia. Nos hará falta 𝑐𝑐𝑣𝑣 para calcular estas variaciones de energía interna. Lo haremos de la siguiente manera: 𝛾𝛾 = 𝑐𝑐𝑝𝑝 𝑐𝑐𝑣𝑣 = 𝑐𝑐𝑣𝑣 + 𝑅𝑅 𝑐𝑐𝑣𝑣 ⟹ 𝑐𝑐𝑣𝑣 = 𝑅𝑅 𝛾𝛾 + 1 Lo que da 𝑐𝑐𝑣𝑣 = 0.205 atm ⋅ L mol ⋅ K⁄ . Por tanto: 𝑊𝑊𝑒𝑒 = 𝑛𝑛𝑐𝑐𝑣𝑣��𝑇𝑇𝐴𝐴𝐴𝐴 − 𝑇𝑇𝐴𝐴𝐴𝐴� + �𝑇𝑇𝐵𝐵𝐵𝐵 − 𝑇𝑇𝐵𝐵𝐵𝐵 �� = (8 mol) ⋅ �0.205 atm ⋅ L K ⋅ mol � ⋅ (−1172 K) = −1922 atm ⋅ L Desde el punto de vista del gas, este trabajo es negativo porque un agente externo lo está efectuando sobre el mismo. El trabajo intercambiado por la resistencia tendría signo positivo. d) El gas en B experimenta un proceso adiabático reversible, así que su entropía permanece invariante: ∆𝑆𝑆𝐵𝐵 = 0 Por otra parte, la variación de entropía del gas en A la podemos determinar a partir de la expresión: ∆𝑆𝑆𝐴𝐴 = 𝑛𝑛𝑐𝑐𝑣𝑣 ln 𝑇𝑇𝐴𝐴𝐴𝐴 𝑇𝑇𝐴𝐴𝐴𝐴 + 𝑛𝑛𝑛𝑛 ln 𝑉𝑉 𝐴𝐴𝐴𝐴 𝑉𝑉𝐴𝐴𝐴𝐴 Sustituyendo: ∆𝑆𝑆𝐴𝐴 = (8 mol) ⋅ �0.205 atm ⋅ L K ⋅ mol � ⋅ ln 1356.9 293.15 + (8 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ ln 296.7 192.2 = 2.80 atm ⋅ L K MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 18. 16.- Un gas ideal monoatómico ocupa un recipiente cilíndrico cerrado mediante un émbolo de peso despreciable y que puede moverse sin fricción. Su sección es S = 1000 cm2 y la presión externa es en todo momento de 1 atm. Las paredes laterales del cilindro y del émbolo son adiabáticas, pero la base es diaterma, de manera que existe contacto con un foco térmico. El gas describe un ciclo formado por los cuatro procesos irreversibles siguientes, partiendo de un estado inicial dado por 1 atm, 300 K y 60 litros: 1-2: se mantiene en todo momento el gas en contacto con un foco de 300 K, se coloca una masa M = 100 kg sobre el émbolo y el gas se comprime hasta un nuevo estado de equilibrio de volumen V2. 2-3: se comprime hasta un nuevo estado de equilibrio, con un volumen V3, manteniendo la masa M pero cambiando el foco de 300 K por otro de 200 K. 3-4: se expande hasta un nuevo volumen V4 manteniendo el foco de 200 K y retirando la masa M. 4-1: vuelve al estado inicial de equilibrio al cambiar el foco de 200 K por uno de 300 K. Calcular: (a) Las coordenadas termodinámicas de los estados 2,3 y 4. (b) La variación de energía interna del gas en los dos primeros procesos. (c) El trabajo neto del ciclo y el calor intercambiado con los dos focos térmicos. (d) La variación de entropía del universo en un ciclo. a) Antes de nada, calculamos el número de moles de gas: 𝑛𝑛 = 𝑝𝑝1 𝑉𝑉1 𝑅𝑅𝑇𝑇1 = (1 atm) ⋅ (60 L) �0.082 atm ⋅ L K ⋅ mol� ⋅ (300 K) = 2.44 mol (2) Como el gas está en todo momento en contacto con el foco caliente, su temperatura no se modifica: 𝑇𝑇2 = 300 K. En el estado de equilibrio, la presión del gas se ha igualado a la externa. Así: 𝑝𝑝2 = 𝑝𝑝𝑎𝑎𝑎𝑎𝑎𝑎 + 𝑀𝑀𝑀𝑀 𝑆𝑆 = 1 atm + (100 kg) ⋅ (9.81 m s2 ⁄ ) 1000 ⋅ 10−4 m2 ⋅ 1 atm 101300 Pa = 1.10 atm Con estas variables, hallamos el volumen: 𝑉𝑉2 = 𝑛𝑛𝑛𝑛𝑇𝑇2 𝑝𝑝2 = (2.44 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (300 K) (1.10 atm) = 54.6 L (3) La masa sobre el émbolo no cambia, así que tampoco lo hará la presión. 𝑝𝑝3 = 1.10 atm. La temperatura final ha de coincidir con la del nuevo foco, 𝑇𝑇3 = 200 K. Como en el caso anterior, obtenemos el volumen de la ecuación de estado: 𝑉𝑉3 = 𝑛𝑛𝑛𝑛𝑇𝑇3 𝑝𝑝3 = (2.44 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (200 K) (1.10 atm) = 36.4 L (4) Se mantiene el foco frío, de modo que 𝑇𝑇4 = 200 K. Asimismo, hemos retirado la masa que inicialmente depositamos sobre el émbolo: 𝑝𝑝4 = 𝑝𝑝𝑎𝑎𝑎𝑎𝑎𝑎 = 1 atm. Como ya es costumbre, el volumen es: 𝑉𝑉4 = 𝑛𝑛𝑛𝑛𝑇𝑇4 𝑝𝑝3 = (2.44 mol) ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (200 K) (1 atm) = 40 L 𝟏𝟏 𝟐𝟐 𝟑𝟑 𝟒𝟒 𝑽𝑽 (L) 𝟔𝟔𝟔𝟔 𝟓𝟓𝟓𝟓. 𝟔𝟔 𝟑𝟑𝟑𝟑. 𝟒𝟒 𝟒𝟒𝟒𝟒 𝒑𝒑 (atm) 𝟏𝟏 𝟏𝟏. 𝟏𝟏𝟏𝟏 𝟏𝟏. 𝟏𝟏𝟏𝟏 𝟏𝟏 𝑻𝑻 (K) 𝟑𝟑𝟑𝟑𝟑𝟑 𝟑𝟑𝟑𝟑𝟑𝟑 𝟐𝟐𝟐𝟐𝟐𝟐 𝟐𝟐𝟐𝟐𝟐𝟐 MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 19. b) Las variaciones de energía interna dependerán exclusivamente de las temperaturas iniciales y finales, pues el sistema considerado es un gas ideal. Por consiguiente, como el primer proceso es isotermo, ∆𝑈𝑈12 = 0. Para el segundo: ∆𝑈𝑈23 = 𝑛𝑛𝑐𝑐𝑣𝑣(𝑇𝑇3 − 𝑇𝑇2) = (2.44 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (−100 K) = −30 atm ⋅ L c) Los cuatro procesos son expansiones o compresiones frente a una presión exterior constante: 𝑊𝑊12 = 𝑝𝑝2(𝑉𝑉2 − 𝑉𝑉1) = (1.10 atm) ⋅ (−5.4 L) = −5.9 atm ⋅ L 𝑊𝑊23 = 𝑝𝑝3(𝑉𝑉3 − 𝑉𝑉2) = (1.10 atm) ⋅ (−18.2 L) = −20 atm ⋅ L 𝑊𝑊34 = 𝑝𝑝4(𝑉𝑉4 − 𝑉𝑉3) = (1 atm) ⋅ (3.6 L) = 3.6 atm ⋅ L 𝑊𝑊41 = 𝑝𝑝1(𝑉𝑉1 − 𝑉𝑉4) = (1 atm) ⋅ (20 L) = 20 atm ⋅ L El trabajo neto en un ciclo vale: 𝑊𝑊 = −5.9 − 20 + 3.6 + 20 atm ⋅ L = −2.3 atm ⋅ L Los calores los podemos despejar directamente de la expresión del primer principio: 𝑄𝑄12 = 𝑊𝑊12 = −5.9 atm ⋅ L 𝑄𝑄23 = −30 − 20 atm ⋅ L = −50 atm ⋅ L 𝑄𝑄34 = −3.6 atm ⋅ L 𝑄𝑄41 = 20 atm ⋅ L + (2.44 mol) ⋅ 3 2 ⋅ �0.082 atm ⋅ L K ⋅ mol � ⋅ (100 K) = 50 atm ⋅ L En concreto, los calores 𝑄𝑄12 y 𝑄𝑄41 se intercambian con el foco caliente y los calores 𝑄𝑄23 y 𝑄𝑄34, con el foco frío. El calor neto intercambiado con cada foco (desde el punto de vista del foco) es: 𝑄𝑄FOCO CALIENTE = −(−5.9 + 50 atm ⋅ L) = −44.1 atm ⋅ L 𝑄𝑄FOCO FRÍO = −(−50 − 3.6 atm ⋅ L) = 53.6 atm ⋅ L d) En un ciclo: ∆𝑆𝑆UNIVERSO = ∆𝑆𝑆GAS + ∆𝑆𝑆FOCOS Como la entropía es una función de estado, ∆𝑆𝑆GAS = 0 y queda: ∆𝑆𝑆UNIVERSO = ∆𝑆𝑆FOCOS = ∆𝑆𝑆FOCO CALIENTE + ∆𝑆𝑆FOCO FRÍO Por otra parte: ∆𝑆𝑆FOCO CALIENTE = 𝑄𝑄FOCO CALIENTE 𝑇𝑇1 = −44.1 atm ⋅ L 300 K = −0.15 atm ⋅ L K ∆𝑆𝑆FOCO FRÍO = 𝑄𝑄FOCO FRÍO 𝑇𝑇3 = 53.6 atm ⋅ L 200 K = 0.27 atm ⋅ L K En conclusión: ∆𝑆𝑆UNIVERSO = −0.15 + 0.27 atm ⋅ L K = 0.12 atm ⋅ L K MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 20. 17.- Un trozo de metal de 200 g de masa y calor específico 0.60 cal/gº⋅C se encuentra a la temperatura de 227 ºC. Para enfriarlo, se introduce en primer lugar en un gran recipiente que contiene agua en su punto de ebullición y, a continuación, se sumerge en el mar, que está a una temperatura de 17 ºC. Detallando y razonando los cálculos realizados, obtener la variación de entropía del universo durante este proceso. El cálculo de la variación de entropía es análogo para los dos procesos, pues en ambos interactúa un sistema de temperatura variable con un foco térmico. Para determinar la variación de entropía del universo en este tipo de procesos, habremos de calcular por separado la que experimentan las sustancias involucradas. El intercambio de calor por parte de un sistema que interactúa con un único es un proceso irreversible. Para poder aplicar la expresión ∆𝑆𝑆 = ∫ 𝛿𝛿𝛿𝛿 𝑇𝑇𝑅𝑅 , buscamos un proceso termodinámico cuyos estados inicial y final coincidan con los del proceso en cuestión. Dado que la entropía es una función de estado, sus variaciones no dependen del proceso sino únicamente de los estados extremos. Para que un sistema modifique su temperatura de forma reversible, debe hacerlo de forma que su temperatura varíe infinitesimalmente, para lo cual se requieren infinitos focos. En este contexto, cada cambio diferencial en la entropía del sistema se podría expresar como: d𝑆𝑆 = 𝑚𝑚𝑐𝑐d𝑇𝑇 𝑇𝑇 La variación de entropía asociada a un cambio finito en la temperatura del sistema se obtendría integrando: ∆𝑆𝑆SISTEMA = � 𝑚𝑚𝑚𝑚d𝑇𝑇 𝑇𝑇 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 = 𝑚𝑚𝑚𝑚 ln 𝑇𝑇𝑓𝑓 𝑇𝑇𝑖𝑖 En lo que al foco respecta, se considera que intercambia calor reversiblemente, de forma que no es necesario encontrar un segundo proceso con los mismos estados de partida y de llegada. Directamente: ∆𝑆𝑆FOCO = � 𝛿𝛿𝛿𝛿 𝑇𝑇𝑅𝑅 = |𝑄𝑄| 𝑇𝑇 = 𝑚𝑚𝑚𝑚|∆𝑇𝑇SISTEMA| 𝑇𝑇 Ya que la temperatura de un foco térmico es constante. La variación de entropía del universo se obtendrá como la suma de las dos variaciones de entropía mencionadas. Todas las temperaturas se introducirán en kelvin. A continuación, aplicamos las ecuaciones deducidas arriba a los dos procesos de transferencia de calor indicados en el enunciado. Notamos que el comportamiento del agua en ebullición y del mar se halla muy próximo al de un foco térmico, ya que sus capacidades caloríficas son muy elevadas en relación al valor de los calores puestos en juego. Para el proceso de enfriamiento en el recipiente con agua en ebullición: ∆𝑆𝑆SISTEMA,I = (200 g) ⋅ �0.60 cal g ⋅ °C �⋅ ln 373.15 500.15 = −35.2 cal K ∆𝑆𝑆FOCO,I = (200 g) ⋅ �0.60 cal g ⋅ °C � ⋅ (127 K) 373.15 K = 40.8 cal K MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es
- 21. Para el proceso de enfriamiento en el mar: ∆𝑆𝑆SISTEMA,I = (200 g) ⋅ �0.60 cal g ⋅ °C �⋅ ln 290.15 373.15 = −30.3 cal K ∆𝑆𝑆FOCO,I = (200 g) ⋅ �0.60 cal g ⋅ °C � ⋅ (83 K) 290.15 K = 34.3 cal K Finalmente: ∆𝑆𝑆UNIVERSO = −35.2 + 40.8 − 30.3 + 34.3 cal K = 9.6 cal K Resulta ∆𝑆𝑆UNIVERSO > 0, lo que implica que, en conjunto, el proceso tratado es irreversible. MARTÍN DE LA ROSA DÍAZ Enero 2016 killer74@hotmail.es