Assignment Chapter - Q & A Compilation by Niraj Thapa

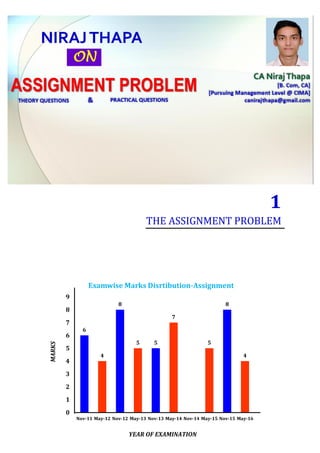
1
THE ASSIGNMENT PROBLEM
6
4
8
5 5
7
5
8
4
0
1
2
3
4
5
6
7
8
9
Nov-11 May-12 Nov-12 May-13 Nov-13 May-14 Nov-14 May-15 Nov-15 May-16
Examwise Marks Disrtibution-Assignment
MARKS
YEAR OF EXAMINATION

Let us start the topic with some questions relating to the topic.
Issue 1: If in a printing press there is one machine and one operator is there to operate. How would the
manager employ the worker? Obviously, the only operator shall operate the machine.
Issue 2: If there are two machines in the press and two operators are engaged at different rates to operate
them. Which operator should operate which machine for minimising the total cost?
Issue 3: If there are n machines available and n persons are engaged at different rates to operate them.
Which operator should be assigned to which machine to ensure maximum efficiency?
The answer to Issue No.2 & 3 is based on the Principle of Assignment Technique (Hungarian Method).
Assignment is optimal if it is in the interest of the press (i.e. the press should be able to maximise its total profit
or minimise the total operating cost)
The problem of assignment arises because available resources such as men, machines, etc. have varying
degrees of efficiency for performing different activities
An assignment is an act to allot the given number of jobs to operators. Assignment problem is one of the
special cases of transportation problems. The objective of the assignment problem is to minimize the cost
(i.e., maximising revenue/profits) or time of completing a number of jobs by a number of persons.
An important characteristic of the assignment problem is the number of sources is equal to the number of
destinations .It is explained in the following way.
 Only one job is assigned to person
 Each person is assigned with exactly one job
The assignment problem involves following steps to get optimal solution.
I. Initial Solution
II. Optimality Test
III. Assigning Jobs
EXPLAINED
I. Initial Solution
The problem will specify jobs, operators and their associated costs. The no. of jobs should be equal
to the no. of operators. It should be in matrix form.
Start with a balanced minimisation* matrix.
a) Row Reduction (The minimum cost of each row should be deducted from all cell cost of that row)
b) Column Reduction (Deduct minimum cost of each column from all cost cell of that column)
(Perform column operation in matrix obtained after Row Reduction)
II. Optimality Test
The matrix obtained after initial solution is to be tested for optimality.
In this step the objective is to cover maximum zeros by drawing minimum no. of straight lines
(straight lines means not diagonal lines)
Then check whether the no. of straight lines drawn equals no. of row (column).
If the answer is affirmative# then the solution is optimal.
INTRODUCTION
STEPS INVOLVED

1
III. Assigning Jobs
Start from the first row and see if there is single zero$ row, if yes then allot job over that zero by
marking square sign  over this zero and cross (X) all zeros against the column where  is allotted.
Repeat the same process for remaining rows and proceed in a similar way for all columns.
Finally write the combination of operators/workers and job along with cost and take the total cost.
The total cost will be minimum.
1) *Treatment of Unbalanced Maximisation Matrix
A matrix is said to be balanced if No. of rows = No. of columns, otherwise it will be an unbalanced matrix.
An unbalanced matrix is to be balanced by introducing a dummy row or column (whichever is necessary)
so as to proceed further.
A minimisation matrix has the objective of minimising cost or time. A matrix with the objective of
maximising profit/revenue is a maximisation matrix. A maximisation matrix is to be converted in to the
minimisation matrix by the following steps:
a) Select the largest cell cost from the entire matrix
b) Deduct all cell costs from the cell element selected in (a) above and proceed further.
In case of unbalanced matrix with maximisation objective, we do have the options either to
a) Minimise the matrix and then balance the matrix OR
b) Balance the matrix and minimise the matrix
(There will be no change in optimal solution)
2) # What if no. of straight lines drawn ≠ no. of rows (columns)
In such cases the solution is to be improved before assigning jobs and should be tested for optimality.
How to improve the matrix?
 Pick the minimum uncovered cell cost. (Uncovered element means such element not touched by st.
line)
 Deduct the minimum cell cost from uncovered cells
 Add the said minimum cell cost to intersecting cells (Intersecting cell means two lines have met each
other in that cell)
 In cells where there is single line (i.e. no intersection) no treatment is required. Copy the elements as it
is in the upcoming matrix.
3) $ What if there are more than one zeros in a row/column?
In such cases we shall move forward to next row and subsequent rows thereon and make allotment
where there is one zero. If all rows are finished without any single zero and again we move forward
column wise and proceed further.
4) What if few zeros are left uncovered either by square sign  or cross sign (X)
This case arises when tie appears. Select any one zero arbitrarily and assign it and mark two cross sign
(X) against this zero in Row & Column. Now assign one remaining zero.
5) If a constant is added/multiplied/divided/ subtracted to every element of the matrix in an assignment
problem then an assignment which minimises the total cost for the new matrix will also minimize the
total cost matrix. (i.e. there will be no impact in final solution)
ISSUES IN ABOVE STEPS

2
STEPS IN ASSGNMENT PROBLEM AT A GLANCE
Start
Write the problem
in matrix form
Is it a
balanced
problem?
Add Dummy
Row/Column
Is it a
maximisation
Problem?
Convert it into a
minimisation problem
Obtain reduced cost matrix by
Row & Column Operation
Make assignments on one-to-one
match basis considering zeros in
Rows/columns
Stop
NO
YES
NO
YES

3
Question -1
Prescribe the steps to be followed to solve an assignment problem.
Answer:
The steps involved in assignment problem can be solved by following steps:
Step-1:
Take a balanced minimization matrix and perform Row Reduction Operation by subtracting the minimum
cost of each row from all cell cost of that row and conduct Column Reduction Operation by deducting
minimum cost of each column from all cost cell of that column.
Step-2:
The matrix obtained after initial solution is to be tested for optimality.
In this step the objective is to cover maximum zeros by drawing minimum no. of straight lines (straight
lines mean not diagonal lines)
Then check whether the no. of straight lines drawn equals no. of row (column).
If the answer is affirmative then the solution is optimal
Step-3:
Assigning Jobs
Start from the first row and see if there is single zero row, if yes then allot job over that zero by marking
square sign  over this zero and cross (X) all zeros against the column where  is allotted.
Repeat the same process for remaining rows and proceed in a similar way for all columns.
Finally write the combination of operators/workers and job along with cost and take the total cost.
The total cost will be minimum.
(Read Introduction portion for detailed study)
Question -2
Explain following statement
“Assignment is special case of transportation problem; it can also be solved by transportation methods”
Answer:
The assignment problem is special case of transportation problem; it can also be solved by transportation
method. But the solution obtained by applying this method would be severely degenerate. This is because
the optimality test in the transportation method requires that there must be m+n-1
allocations/assignments. But due to the special structure of assignment problem of order n × n, any
solution cannot have more than n assignments. Thus, the assignment problem is naturally degenerate. In
order to remove degeneracy, (n-1)* number of dummy allocations will be required in order to proceed
with the transportation method. Thus, the problem of degeneracy at each solution makes the
transportation method computationally inefficient for solving an assignment problem.
(*) m+n-1-n n+n-1 – n 2n-1 - n n-1
Question -3
In an assignment problem to assign jobs to men to minimize the time taken, suppose that one man does
not know how to do a particular job, how will you eliminate this allocation from the solution?
Answer:
The objective of assignment problem is to minimize time the total time take to perform a particular task or
to minimize the overall cost so, in an assignment minimization problem, if one task cannot be assigned to
one person, introduce a prohibitively large cost for that allocation, say M, where M has a high the value.
Then, while doing the row minimum and column minimum operations, automatically this allocation will
get eliminated.
THEORY QUESTIONS [EXAM-SM-PM-RTP-OTHERS]

4
Question -4
Just after row and column minimum operations, we find that a particular row has 2 zeros. Does this imply
that the 2 corresponding numbers in the original matrix before any operation were equal? Why?
Answer:
Under the Hungarian Assignment Method, the prerequisite to assign any job is that each row and column
must have a zero value in its corresponding cells.
If any row or column does not have any zero value then to obtain zero value, each cell values in the row or
column is subtracted by the corresponding minimum cell value of respective rows or columns by
performing row or column operation.
This means if any row or column have two or more cells having same minimum value then these row or
column will have more than one zero.
However, having two zeros does not necessarily imply two equal values in the original assignment matrix just
before row and column operations. Two zeroes in a same row can also be possible by two different operations
i.e. one zero from row operation and one zero from column operation.
Question -5
Under the usual notation, where a32 means the element at the intersection of the 3rd row and 2nd column,
we have, in a 4 × 4 assignment. What can you conclude about the remaining assignments? Why?
Answer:
The order of matrix in the assignment problem is 4 × 4. The total assignment (allocations) will be four.
In the assignment problem when any allocation is made in any cell then the corresponding row and column
become unavailable for further allocation. Hence, these corresponding row and column are crossed mark
to show unavailability.
In the given assignment matrix two allocations have been made in a24 (2nd row and 4th column) and a32
(3rd row and 2nd column).
This implies that 2nd and 3rd row and 4th and 2nd column are unavailable for further allocation.
Therefore, the other allocations are at either at a11 and a43 or at a13 and a41.
Question -6
Explain the following terms:
a) Balanced Problem b) Unbalanced Prob. c) Dummy d) Infeasible Assignment e) Maximisation Prob.
Answer:
Balanced
Problem
An assignment problem is said to be balanced if the no. of rows = no. of columns (i.e. No. of jobs =
no. of workers)
Unbalanced
Problem
If in an assignment problem the no. of rows is not equal to no. of columns the problem is said to
be unbalanced problem. Here, no. of facilities is not equal to the no. of jobs.
Such matrix is to be balanced by inserting requisite no. of dummy row(s)/column(s).
Dummy A dummy is an imaginary job/facility with all cell element being Zero which is introduced to
make an unbalanced problem balanced. In case final allotment is in dummy row/column, then it
and indication that the particular operator has not been assigned any task.
Infeasible
Assignment
Sometimes, it happens that a particular person is unable to perform a specific job/task or a
specific job cannot be performed in a particular machine.
In such cells a very high cost is assigned so as to avoid the infeasibility and continue the solution.
Maximisation
Problem
In a maximisation problem the objective is to maximise the sales/revenue/profit. This is to be
converted into minimisation problem.
A maximisation matrix is to be converted in to the minimisation matrix by the following steps:
b) Deduct all cell costs from the cell element selected in (a) above.

5
liahf;auofahofhuaofuafaw
Question -1
An Accounts Officer has 4 subordinates and 4 tasks. The subordinates differ in efficiency. The tasks also
differ in their intrinsic difficulty. His estimates of the time each would take to perform each task is given in
the matrix below. How should the tasks be allocated one to one man, so that the total man hours are
minimized?
Solution:
The given problem is a balanced minimisation problem.
Step I: Initial Solution
a) Row Reduction
0 18 9 3
9 2 0 22
23 4 3 0
9 16 14 0
b) Column Reduction
0 14 9 3
9 20 0 22
23 0 3 0
9 12 14 0
Step II: Optimality Test
We draw minimum no. of straight lines to cover maximum zeros.
0 14 9 3
9 20 0 22
23 0 3 0
9 12 14 0
Since the no. of lines = No. of row/column=4, optimal solution is possible.
Step III: Assignment Final Solution
0 14 9 3
9 20 0 22
23 0 3 0
9 12 14 0
Subordinates
Tasks
I II III IV
1 8 26 17 11
2 13 28 4 26
3 38 19 18 15
4 19 26 24 10
Subordinates Tasks Time
1 I 8
2 III 4
3 II 19
4 IV 10
Total Time 41
PRACTICAL QUESTIONS [EXAM-SM-PM-RTP-OTHERS]

6
Question -2
A manager has 5 jobs to be done. The following matrix shows the time taken by the j-th job (j = 1,2...5) on
the i-th machine (i = I,II,III…V). Assign 5 jobs to the 5 machines so that the total time taken is minimized.
Jobs
Machines 1 2 3 4 5
I 9 3 4 2 10
II 12 10 8 11 9
III 11 2 9 0 8
IV 8 0 10 2 1
V 7 5 6 2 9
Solution:
The given problem is a balanced minimisation problem.
a) Row Reduction
7 1 2 0 8
4 2 0 3 1
11 2 9 0 8
8 0 10 2 1
5 3 4 0 7
b) Column Reduction
3 1 2 0 7
0 2 0 3 0
7 2 9 0 7
4 0 10 2 0
1 3 4 0 6
3 1 2 0 7
0 2 0 3 0
7 2 9 0 7
4 0 10 2 0
1 3 4 0 6
Since, the no. of lines ≠ No. of row/column, optimal solution is not possible. We further improve the
matrix.
.
 Pick the minimum uncovered cell cost.
 Deduct the minimum cell cost from
uncovered cells
 Add the said minimum cell cost to
intersecting cells
 Copy the remaining elements in the
coming matrix as it is.

7
Here, the minimum uncovered cell element is 1, we shall proceed further with the steps stated above.
Finally we get the following matrix.
2 0 1 0 6
0 2 0 4 0
6 1 8 0 6
4 0 10 3 0
0 2 3 0 5
We again draw minimum no. of straight lines to cover maximum zeros.
2 0 1 0 6
0 2 0 4 0
6 1 8 0 6
4 0 10 3 0
0 2 3 0 5
Since, the no. of lines = No. of row/column = 5, optimal solution is possible.
Step III: Assignment
2 0 1 0 6
0 2 0 4 0
6 1 8 0 6
4 0 10 3 0
0 2 3 0 5
Final Answer
Machines Jobs Time
I 2 3
II 3 8
III 4 0
IV 5 1
V 1 7
Total Time 19

8
Question -3
5 salesmen are to be assigned to 5 districts. Estimates of sales revenue in thousands of rupees for each
salesman are given below. Find the assignment pattern that maximizes the sales revenue.
A B C D E
1 32 38 40 28 40
2 40 24 28 21 36
3 41 27 33 30 37
4 22 38 41 36 36
5 29 33 40 35 39
Solution:
The given problem is a balanced maximisation problem, so at first we need to convert the matrix into
cost/loss matrix.
The cost matrix will be as:
9 3 1 13 1
1 17 13 20 5
0 14 8 11 4
19 3 0 5 5
12 8 1 6 2
a) Row Reduction
8 2 0 12 0
0 16 12 19 4
0 14 8 11 4
19 3 0 5 5
11 7 0 5 1
b) Column Reduction
8 0 0 7 0
0 14 12 14 4
0 12 8 6 4
19 1 0 0 5
11 5 0 0 1
8 0 0 7 0
0 14 12 14 4
0 12 8 6 4
19 1 0 0 5
11 5 0 0 1
A maximization matrix is to be converted in to the
minimization matrix:
b) Deduct all cell costs from the cell element
selected in (a) above and proceed further.

9
Since, the no. of lines drawn ≠ No. of row/column, optimal solution is not possible. We further improve
the matrix. The minimum uncovered element is 4 that is subtracted from all elements and added to all
elements at intersections. This yields the following matrix in which 5 lines are needed to cover all zeros.
We again draw minimum no. of straight lines to cover maximum zeros.
Here by following the steps we first allot at cell12 [12 means 1st Row 2nd Column] now tie appears as there
are more than one zeros in remaining rows/columns.
So, we arbitrarily allot assignment in Cell21
[Note: You may allot in any cells containing Zero other than elements at Column 2 & Row 1]
Again tie appears in Cell43, Cell44, and Cell53 & Cell54
We make arbitrary allotment in Cell54 and proceed further.
Final Answer
Salesman District Sales (Rs. In ‘000)
1 B 38
2 A 40
3 E 37
4 C 41
5 D 35
Total Sales 191
12 0 0 7 0
0 10 8 10 0
0 8 4 2 0
23 1 0 0 5
15 5 0 0 1
12 0 0 7 0
0 10 8 10 0
0 8 4 2 0
23 1 0 0 5
15 5 0 0 1
12 0 0 7 0
0 10 8 10 0
0 8 4 2 0
23 1 0 0 5
15 5 0 0 1
uncovered cells
intersecting cells

10
Question -4
To stimulate interest and provide an atmosphere for intellectual discussion, a finance faculty in a
management school decides to hold special seminars on four contemporary topics– leasing, portfolio
management, private mutual funds, swaps and options. Such seminars should be held once a week in the
afternoons. However, scheduling these seminars (one for each topic, and not more than one seminar per
afternoon) has to be done carefully so that the number of students unable to attend is kept to a minimum.
A careful study indicates that the number of students who cannot attend a particular seminar on a specific
day is as follows:
Leasing
Portfolio
Management
Private
Mutual Funds
Swaps &
Options
Monday 50 40 60 20
Tuesday 40 30 40 30
Wednesday 60 20 30 20
Thursday 30 30 20 30
Friday 10 20 10 30
Solution:
The given problem is an unbalanced minimisation problem.
The matrix is unbalanced since No. of rows (5) ≠ No. of columns (4). We add a dummy column with all its
elements 0 to balance the matrix. The above matrix will be as follows:
Leasing
Portfolio
Management
Private
Mutual Funds
Swaps &
Options Dummy
Monday 50 40 60 20 0
Tuesday 40 30 40 30 0
Wednesday 60 20 30 20 0
Thursday 30 30 20 30 0
Friday 10 20 10 30 0
a) Row Reduction is not required since all rows have at least one zero element.
[Even if we proceed for row operation there will be no change in the matrix]
b) Column Reduction
40 20 50 0 0
30 10 30 10 0
50 0 20 0 0
20 10 10 10 0
0 0 0 10 0

11
40 20 50 0 0
30 10 30 10 0
50 0 20 0 0
20 10 10 10 0
0 0 0 10 0
Since the no. of lines ≠ No. of row/column, optimal solution is not possible, we further improve the
matrix. The matrix after improvement will be as follows:
40 20 50 0 10
20 0 20 0 0
50 0 20 0 10
10 0 0 0 0
0 0 0 10 10
40 20 50 0 10
20 0 20 0 0
50 0 20 0 10
10 0 0 0 0
0 0 0 10 10
Final Answer
Days Seminars No. of Students
Monday Swaps & Options 20
Tuesday Dummy 0
Wednesday Portfolio Management 20
Thursday Private Mutual Funds 20
Friday Leasing 10
Total 70
The total number of students who will be missing at least one seminar = 70
uncovered cells
intersecting cells

12
Question -5
A solicitor's firm employs typists on hourly piece-rate basis for their daily work. There are five typists for
service and their charges and speeds are different. According to an earlier understanding only one job is
given to one typist and the typist is paid for full hours even if he works for a fraction of an hour. Find the
least cost allocation for the following data:
Solution:
First of all we shall find the no. of hours required by each typist to complete the particular jobs.
The matrix will be as follows:
Now we shall change the above matrix into cost matrix by multiplying the cell elements by hourly rate.
P Q R S T
A 85 75 65 125 75
B 90 78 66 132 78
C 75 66 57 114 69
D 80 72 60 120 72
E 76 64 56 112 68
The matrix is a balanced minimisation matrix we shall proceed further.
a) Row Reduction
20 10 0 60 10
24 12 0 66 12
18 9 0 57 12
20 12 0 60 12
20 8 0 56 12
Job
No. of
Pages
P 199
Q 175
R 145
S 298
T 178
Typist
Rate/hour
(Rs)
No. of pages
typed/hour
A 5 12
B 6 14
C 3 8
D 4 10
E 4 11
P Q R S T
A 17 15 13 25 15
B 15 13 11 22 13
C 25 22 19 38 23
D 20 18 15 30 18
E 19 16 14 28 17
P Q R S T
A 199/12 175/12 145/12 298/12 178/12
B 199/14 175/14 145/14 298/14 178/14
C 199/8 175/8 145/8 298/8 178/8
D 199/10 175/10 145/10 298/10 178/10
E 199/11 175/11 145/11 298/11 178/11

13
b) Column Reduction
2 2 0 4 0
6 4 0 10 2
0 1 0 1 2
2 4 0 4 2
2 0 0 0 2
2 2 0 4 0
6 4 0 10 2
0 1 0 1 2
2 4 0 4 2
2 0 0 0 2
Since the no. of lines ≠ No. of row/column, optimal solution is not possible. We further improve the
matrix for obtaining optimal solution.
2 1 0 3 0
6 3 0 9 2
0 0 0 0 2
2 3 0 3 2
3 0 1 0 3
Again, the minimum number of lines required to cover all the zeros is only 4 (< 5), optimal assignment
cannot be made at this stage also. We again improve the matrix.
1 0 0 2 0
5 2 0 8 2
0 0 1 0 3
1 2 0 2 2
3 0 2 0 4
Again, the minimum number of lines required to cover all the zeros is only 4 (< 5), optimal assignment
cannot be made at this stage also. We again improve the matrix.
1 0 1 2 0
4 1 0 7 1
0 0 2 0 3
0 1 0 1 1
3 0 3 0 4

14
1 0 1 2 0
4 1 0 7 1
0 0 2 0 3
0 1 0 1 1
3 0 3 0 4
Final Answer
Typist Job Amount
A T 75
B R 66
C S 114
D P 80
E Q 64
Total 399
[Alternative solution also exists since there appears tie.]

15
Question -6
WELLDONE Company has taken the third floor of a multi-storied building for rent with a view to locate one
of their zonal offices. There are five main rooms in this floor to be assigned to five managers. Each room
has its own advantages and disadvantages. Some have windows, some are closer to the washrooms or to
the canteen or secretarial pool. The rooms are of all different sizes and shapes. Each of the five managers
was asked to rank their room preferences amongst the rooms 301, 302, 303,304 and 305. Their
preferences were recorded in a table as indicated below:
MANAGER
M1 M2 M3 M4 M5
302 302 303 302 301
303 304 301 305 302
304 305 304 304 304
301 305 303
302
Most of the managers did not list all the five rooms since they were not satisfied with some of these rooms
and they have left off these from the list. Assuming that their preferences can be quantified by numbers,
find out as to which manager should be assigned to which room so that their total preference ranking is a
minimum.
Solution:
Let us frame the matrix showing the ranks of the rooms.
Room No.
MANAGER
M1 M2 M3 M4 M5
301 - 4 2 - 1
302 1 1 5 1 2
303 2 - 1 4 -
304 3 2 3 3 3
305 - 3 4 2 -
In a cell (-) indicates that no assignment is to be made in that particular cell. We shall ignore (-) cells for
the purpose of solving the problem. The given problem is a balanced minimisation problem, we proceed
further.
a) Row Reduction
- 3 1 - 0
0 0 4 0 1
1 - 0 3 -
1 0 1 1 1
- 1 2 0 -
b) Column Reduction: Not required

16
- 3 1 - 0
0 0 4 0 1
1 - 0 3 -
1 0 1 1 1
- 1 2 0 -
Final Answer
- 3 1 - 0
0 0 4 0 1
1 - 0 3 -
1 0 1 1 1
- 1 2 0 -
Room No. Manager Rank
301 M5 1
302 M1 1
303 M3 1
304 M2 2
305 M4 2
Total Min. Ranking 7

17
Question -7
An organisation producing 4 different products viz. A, B, C and D having 4 operators viz. P,Q,R and S, who
are capable of producing any of the four products, work effectively 7 hours a day. The time (in minutes)
required for each operator for producing each of the product are given in the cells of the following matrix
along with profit (Rs. per unit).
Product
Operator A B C D
P 6 10 14 12
Q 7 5 3 4
R 6 7 10 10
S 20 10 15 15
Profit/Unit 3 2 4 1
Find out the assignment of operators to products which will maximize the profit.
Solution:
Total time available to each operator = 7 hours = (7x60) minutes = 420 minutes.
At first we calculate the no. of units produced by each operator and then make a profit matrix and finally
convert the matrix into loss/cost matrix.
The above formulate matrix is a balanced maximisation matrix, we will convert the matrix into loss
matrix which will be as:
350 476 440 525
380 392 0 455
350 440 392 518
497 476 448 532
a) Row Reduction
0 126 90 175
380 392 0 455
0 90 42 168
49 28 0 84
Operator
Product (Units)
A B C D
P 70 42 30 35
Q 60 84 140 105
R 70 60 42 42
S 21 42 28 28
Operator
Profit Matrix (In Rs.)
A B C D
P 210 84 120 35
Q 180 168 560 105
R 210 120 168 42
S 63 84 112 28

18
b) Column Reduction
0 98 90 91
380 364 0 371
0 62 42 84
49 0 0 0
0 98 90 91
380 364 0 371
0 62 42 84
49 0 0 0
Since the no. of lines ≠ No. of row/column, optimal solution is not possible. We further improve the
matrix. The improved matrix will be:
0 36 90 29
380 302 0 309
0 0 42 22
111 0 62 0
Step III: Assignment Final Answer
Operator Products Profit
P A 210
Q C 560
R B 120
S D 28
Total 918
0 36 90 29
380 302 0 309
0 0 42 22
111 0 62 0

19
Question -8
A firm produces four products. There are four operators who are capable of producing any of these four
products. The processing time varies from operator to operator. The firm records 8 hours a day and allow
30 minutes for lunch. The processing time in minutes and the profit for each of the products are given
below:
Products
Operators A B C D
1 15 9 10 6
2 10 6 9 6
3 25 15 15 9
4 15 9 10 10
Profit/Unit 8 6 5 4
Find the optimal assignment of products to operators.
Solution:
Productive time per worker = [8hrs. x 60]-30 = 450 mins.
Calculating the no. of units of produced by each operators.
A B C D
1 30 50 45 75
2 45 75 50 75
3 18 30 30 50
4 30 50 45 45
Since we are given the profit per unit of each product, the profit matrix is computed as given below:
Profit Matrix
A B C D
1 240 300 225 300
2 360 450 250 300
3 144 180 150 200
4 240 300 225 180
Converting the contribution matrix into cost matrix.
210 150 225 150
90 0 200 150
306 270 300 250
210 150 225 270

20
a) Row Reduction
60 0 75 0
90 0 200 150
56 20 50 0
60 0 75 120
b) Column Reduction
4 0 25 0
34 0 150 150
0 20 0 0
4 0 25 120
4 0 25 0
34
0
150 150
0 20 0
0
4 0 25 120
The minimum number of lines required to cover all the zeros is only 3(< 4), optimal assignment cannot
be made at this stage also. We improve the matrix.
0 0 21 0
30 0 146 150
0 24 0 4
0 0 21 120
Operators Products Profit
1 D 300
2 B 450
3 C 150
4 A 240
Total 1140
0 0 21 0
30 0 146 150
0 24 0 4
0 0 21 120

21
Question -9
Five lathes are to be allotted to five operators (one for each). The following table gives weekly output
figures (in pieces)-
Operator
Weekly Output in Lathe
L1 L2 L3 L4 L5
P 20 22 27 32 36
Q 19 23 29 34 40
R 23 28 35 39 34
S 21 24 31 37 42
T 24 28 31 36 41
Profit per piece is Rs. 25.
Required: Find the maximum profit per week.
Solution:
The given assignment problem is a maximization problem. We convert it into an opportunity loss matrix
by subtracting all the elements of the given table from the highest element of the table that is 42.
The cost matrix will be as follows:
a) Row Reduction
16 14 9 4 0
21 17 11 6 0
16 11 4 0 5
21 18 11 5 0
17 13 10 5 0
b) Column Reduction
0 3 5 4 0
5 6 7 6 0
0 0 0 0 5
5 7 7 5 0
1 2 6 5 0
Operator L1 L2 L3 L4 L5
P 22 20 15 10 6
Q 23 19 13 8 2
R 19 14 7 3 8
S 21 18 11 5 0
T 18 14 11 6 1

22
0 3 5 4
0
5 6 7 6 0
0 0 0 0 5
5 7 7 5 0
1
2 6 5 0
Since the no. of lines (3) ≠ No. of row/column (5), optimal solution is not possible at this stage. We
further improve the matrix.
0 1 3 2
0
5 4 5 4 0
2 0 0 0 7
5
5
5 3 0
1
0 4 3 0
Again, the minimum number of lines drawn to cover all zeros is 4. Repeating the above steps once again,
we get the following table-
0 1 1 0
0
5 4 3 2 0
4 2 0 0 9
5
5
3 1 0
1 0 2 1 0
The minimum number of lines to cover all zeros is 4 which is less than 5. We further improve the
matrix.
0 2 1 0
1
4 4
2
1 0
4
3 0
0
10
4
5
2 0 0
0 0 1 0 0

23
0 2 1 0 1
4 4 2 1 0
4 3 0 0 10
4 5 2 0 0
0 0 1 0 0
The maximum profit per week is Rs.4,000 (25 × 160).
Operator
Lathe
Machine
Weekly
Output
P L1 20
Q L5 40
R L3 35
S L4 37
T L2 28
Total 160

24
Question -10
A manufacturing company has four zones A, B, C, D and four sales engineers P, Q, R, S respectively for
assignment. Since the zones are not equally rich in sales potential, therefore it is estimated that a
particular engineer operating in a particular zone will bring the following sales:
Zone A: 4,20,000
Zone B: 3,36,000
Zone C: 2,94,000
Zone D: 4,62,000
The engineers are having different sales ability. Working under the same conditions, their yearly sales are
proportional to 14, 9, 11 and 8 respectively. The criteria of maximum expected total sales is to be met by
assigning the best engineer to the richest zone, the next best to the second richest zone and so on.
Find the optimum assignment and the maximum sales.
Solution:
Calculating Sales Matrix
Sales
Man Ratio A B C D
P 14 140000 112000 98000 154000
Q 9 90000 72000 63000 99000
R 11 110000 88000 77000 121000
S 8 80000 64000 56000 88000
Total 42 420000 336000 294000 462000
Dividing all the elements of the matrix by 1000 we get the following matrix.
Converting the revenue matrix into loss matrix we get the following matrix.
Sales
Man A B C D
P 140 112 98 154
Q 90 72 63 99
R 110 88 77 121
S 80 64 56 88
Sales
Man Ratio A B C D
P 14 140 112 98 154
Q 9 90 72 63 99
R 11 110 88 77 121
S 8 80 64 56 88
Total 42 420 336 294 462
If a constant is added/multiplied/divided/
subtracted to every element of the matrix in an
assignment problem then an assignment which
minimises the total cost for the new matrix will
also minimize the total cost matrix. (i.e. there
will be no impact in final solution)

25
a) Row Reduction
14 42 56 0
9 27 36 0
11 33 44 0
8 24 32 0
b) Column Reduction
6 18 24 0
1 3 4 0
3 9 12 0
0 0 0 0
6 18 24 0
1 3 4 0
3 9 12 0
0 0 0 0
The minimum number of lines required to cover all the zeros is only 2 (< 4), optimal assignment cannot
be made at this stage. We improve the matrix and draw minimum no. of straight lines to cover max. zeros
Again, the min. number of lines required to cover all the zeros is only 3 (< 4), optimal assignment cannot
be made at this stage also. We improve the matrix and draw min. no. of straight lines to cover max. Zeros.
5 15 21 0
0 0 1 0
2 6 9 0
2 0 0 3
Again, the min. number of lines required to cover all the zeros is only 3 (< 4), optimal assignment cannot
be made at this stage also. We improve the matrix and draw min. no. of straight lines to cover max. zeros.
5 17 23 0
0 2 3 0
2 8 11 0
0 0 0 1
3 13 19 0
0 0 1 2
0 4 7 0
2 0 0 5

26
Final Answer
Question -11
A company has four zones open and four marketing managers available for assignment. The zones are
not equal in sales potentials. It is estimated that a typical marketing manager operating in each zone
would bring in the following Annual sales:
Zones Rs.
East………………………………………………. 2,40,000
West……………………………………………… 1,92,000
North……………………………………………... 1,44,000
South…………………………………………….. 1,20,000
The four marketing manages are also different in ability. It is estimated that working under the same
conditions, their yearly sales would be proportionately as under:
Manager M………………………………………. 8
Manager N………………………………………. 7
Manager O………………………………………. 5
Manager P………………………………………. 4
Required
If the criterion is maximum expected total sales, find the optimum assignment and the maximum sales.
Solution:
Calculating Sales Matrix
Sales
Man
Ratio East West North South
M 8 80000 64000 48000 40000
N 7 70000 56000 42000 35000
O 5 50000 40000 30000 25000
P 4 40000 32000 24000 20000
Total 24 240000 192000 144000 120000
3 13 19 0
0 0 1 2
0 4 7 0
2 0 0 5
Sales Man Zone Sales Amt.
P D 154000
Q B 72000
R A 110000
S C 56000
Total 392000

27
Dividing all the elements of the matrix by 1000 we get the following matrix.
Sales
Man
Ratio East West North South
M 8 80 64 48 40
N 7 70 56 42 35
O 5 50 40 30 25
P 4 40 32 24 20
Total 24 240 192 144 120
Converting the revenue matrix into loss matrix we get the following matrix.
Manager East West North South
M 0 16 32 40
N 10 24 38 45
O 30 40 50 55
P 40 48 56 60
a) Row Reduction
0 16 32 40
0 14 28 35
0 10 20 25
0 8 16 20
b) Column Reduction
0 8 16 20
0 6 12 15
0 2 4 5
0 0 0 0
0
8 16 20
0 6 12 15
0 2 4 5
0 0 0 0
Since the no. of lines (2) ≠ No. of row/column (4), optimal solution is not possible. We further improve
the matrix.
If a constant is added/multiplied/divided/
subtracted to every element of the matrix in an
assignment problem then an assignment which
minimises the total cost for the new matrix will
also minimize the total cost matrix. (i.e. there
will be no impact in final solution)

28
0
6 14 18
0 4 10 13
0 0 2 3
2 0 0 0
Again no. of lines covering zeros are not equal to the order of matrix, we further improve the matrix.
Again no. of lines covering zeros are not equal to the order of matrix, we further improve the matrix
0
2 10 14
0
0
6 9
4 0 2 3
6 0 0 0
0
2 8 12
0
0
4 7
4 0
0
1
8 2 0 0
0 2 8 12
0 0 4 7
4 0 0 1
8 2 0 0
Sales Man Zones Sales
M East 80,000
N West 56,000
O North 30,000
P South 20,000
Total 1,86,000

29
Question -12
XYZ airline operating 7 days a week has given the following timetable. Crews must have a minimum layover
of 5 hours between flights. Obtain the pairing flight that minimizes layover time away from home. For any
given pairing the crew will be based at the city that results in the smaller layover.
Solution:
To begin with, let us first assume that the crew is based at Chennai. The flight A1, which starts from Chennai
at 6 AM, reaches Mumbai at 8 AM. The schedule time for the flight at Mumbai is 8 AM. Since the minimum
layover time for crew is 5 hours, this flight can depart only on the next day i.e. the layover time will be 24
hours. Similarly, layover times for other flights are also calculated and given in the following table.
The layover times for various flight connections when crew is assumed to be based at Mumbai are similarly
calculated in the following table.
Flight No. Crew based at Mumbai
B1 B2 B3 B4
A1 20 19 14 9
A2 22 21 16 11
A3 28 27 22 17
A4 10 9 28 23
Chennai-Mumbai Mumbai - Chennai
Flight No. Depart. Arrive Flight No. Depart. Arrive
A1 6 AM 8 AM B1 8 AM 10 AM
A2 8 AM 10 AM B2 9 AM 11 AM
A3 2 PM 4 PM B3 2 PM 4 PM
A4 8 PM 10 PM B4 7 PM 9 PM
Flight No.
Crew based at Chennai
B1 B2 B3 B4
A1 24 25 6 11
A2 22 23 28 9
A3 16 17 22 27
A4 10 11 16 21

30
Now since the crew can be based at either of the places, minimum layover times can be obtained for different
flight numbers by selecting the corresponding lower value out of the above two tables. The resulting table is
as given below
A * with an entry in the above table indicates that it corresponds to layover time when the crew is based at
Mumbai. We will now apply the assignment algorithm to find the optimal solution. Subtracting the minimum
element of each row from all the elements of that row, we get the following matrix.
a) Row Reduction
Flight No.
Flight No. B1 B2 B3 B4
A1 14 13 0 3
A2 13 12 7 0
A3 0 1 6 1
A4 1 0 7 12
b) Column Reduction: Not required
Flight No.
A1 14 13 0 3
A2 13 12 7 0
A3 0 1 6 1
A4 1 0 7 12
Flight No.
A1 14 13 0 3
A2 13 12 7 0
A3 0 1 6 1
A4 1 0 7 12
Flight No.
A1 20* 19* 6 9*
A2 22 21* 16* 9
A3 16 17 22 17*
A4 10 9* 16 21
From
Flight To Flight
Lay Over
Time
A1 B3 6
A2 B4 9
A3 B1 16
A4 B2 9
Total 40

31
Question -13
An Electronic Data Processing (EDP) centre has three expert Software professionals. The Centre wants
three application software programs to be developed. The head of EDP Centre estimates the computer
time in minutes required by the experts for development of Application Software Programs as follows-
Software
Programs
Computer Time (in minutes)
Required by Software Professionals
A B C
1 100 85 70
2 50 70 110
3 110 120 130
Assign the software professionals to the application software programs to ensure minimum usage of
computer time.
Solution:
The given problem is a balanced minimization assignment problem.
a) Row Reduction
30 15 0
0 20 60
0 10 20
b) Column Reduction
30 5 0
0 10 60
0 0 20
30 5 0
0 10 60
0 0 20
30 5 0
0 10 60
0 0 20
Software Programs Experts Time
1 C 70
2 A 50
3 B 120
Total 240

32
Question -14
A project consists of four (4) major jobs, for which four (4) contractors have submitted tenders.
The tender amounts, in thousands of rupees, are given below-
Contractors
Job
A B C D
1 120 100 80 90
2 80 90 110 70
3 110 140 120 100
4 90 90 80 90
Find the assignment, which minimizes the total cost of the project. Each contractor has to be assigned one
job.
Solution:
The given problem is a balanced minimization problem.
a) Row Reduction
40 20 0 10
10 20 40 0
10 40 20 0
10 10 0 10
b) Column Reduction
30 10 0 10
0 10 40 0
0 30 20 0
0 0 0 10
30 10 0 10
0 10 40 0
0 30 20 0
0 0 0 10
30 10 0 10
0 10 40 0
0 30 20 0
0 0 0 10
(Note: Alternative solution also exists)
Contractors Job Cost (Rs.'000)
1 C 80
2 D 70
3 A 110
4 B 90
Total 350

33
Question -15
A Marketing Manager has 4 subordinates and 4 tasks. The subordinates differ in efficiency. The tasks also
differ in their intrinsic difficulty. His estimates of the time each subordinate would take to perform each
task is given in the matrix below.
I II III IV
1 16 52 34 22
2 26 56 8 52
3 76 38 36 30
4 38 52 48 20
How should the task be allocated one to one man so that the total man-hours are minimised?
Solution:
The given problem is a balanced minimization problem.
a) Row Reduction
0 36 18 6
18 48 0 44
46 8 6 0
18 32 28 0
b) Column Reduction
0 28 18 6
18 40 0 44
46 0 6 0
18 24 28 0
0 28 18 6
18 40 0 44
46 0 6 0
18 24 28 0
0 28 18 6
18 40 0 44
46 0 6 0
18 24 28 0
Operator Task Time (Hrs)
1 I 16
2 III 8
3 II 38
4 IV 20
Total 82

34
Question -16
Five swimmers are eligible to compete in a relay team which is to consist of four swimmers swimming four
different swimming styles ; back stroke breast stroke, free style and butterfly. The time taken for the five
swimmers – Anand, Bhaskar, Chandru, Dorai and Easwar- to cover a distance of 100 meters in various
swimming styles are given below in minutes : seconds. Anand swims the back stroke in 1:09, the breast
stroke in 1:15 and has never competed in the free style or butterfly. Bhaskar is a free style specialist
averaging 1:01 for the 100 metres but can also swim the breast stroke in 1:16 and butterfly in 1:20.
Chandru swims all styles – back stroke 1:10, butterfly 1:12, free style 1:05 and breast stroke 1:20. Dorai
swims only the butterfly 1:11 while Easwar swims the back stroke 1:20, the breast stroke 1:16, the free
style 1:06 and the butterfly 1:10.
Required
Which swimmers should be assigned to which swimming style? Who will be in the relay?
Solution:
First of all we shall make assignment matrix with time expressed in seconds. The matrix table will be:
Back
Stroke
Breast
Stroke
Free
Style Butterfly
Anand 69 75 - -
Bhaskar - 76 61 80
Chandru 70 80 65 72
Dorai - - - 71
Easwar 80 76 66 70
Since the matrix is unbalanced, we make the matrix balanced by inserting a dummy column and proceed
further.
Back
Stroke
Breast
Stroke
Free
Style Butterfly Dummy
Anand 69 75 - - 0
Bhaskar - 76 61 80 0
Chandru 70 80 65 72 0
Dorai - - - 71 0
Easwar 80 76 66 70 0
a) Row Reduction: Not Required [Since each row has at least one element as Zero]
b) Column Reduction
0 0 - - 0
- 1 0 10 0
1 5 4 2 0
- - - 1 0
11 1 5 0 0

35
0 0 - - 0
- 1 0 10 0
1 5 4 2 0
- - - 1 0
11 1 5 0 0
0 0 - - 1
- 0 0 10 0
0 4 4 2 0
- - - 1 0
10 0 5 0 0
Question -17
ABC Company is engaged in manufacturing 5 brands of packet snacks. It is having five manufacturing
setups, each capable of manufacturing any of its brands, one at a time. The cost to make a brand on these
setups vary according to following table-
Required:
Assuming five setups are S1, S2, S3, S4, and S5 and five brands are B1, B2, B3, B4, and B5, Find the
optimum assignment of the products on these setups resulting in the minimum cost.
Swimmers Style Time
Anand Back Stroke 75
Bhaskar Free Style 61
Chandru Back Stroke 70
Dorai Dummy 0
Easwar Butterfly 70
Total Time (Seconds) 276
0 0 - - 1
- 0 0 10 0
0 4 4 2 0
- - - 1 0
10 0 5 0 0
S1 S2 S3 S4 S5
B1 4 6 7 5 11
B2 7 3 6 9 5
B3 8 5 4 6 9
B4 9 12 7 11 10
B5 7 5 9 8 11
uncovered cells
intersecting cells

36
Solution:
a) Row Reduction
0 2 3 1 7
4 0 3 6 2
4 1 0 2 5
2 5 0 4 3
2 0 4 3 6
b) Column Reduction
0 2 3 0 5
4 0 3 5 0
4 1 0 1 3
2 5 0 3 1
2 0 4 2 4
0 2 3 0 5
4 0 3 5 0
4 1 0 1 3
2 5 0 3 1
2 0 4 2 4
0 3 4 0 6
3 0 3 4 0
3 1 0 0 3
1 5 0 2 1
1 0 4 1 4
Brands Setup Costs
B1 S1 4
B2 S5 5
B3 S4 6
B4 S3 7
B5 S2 5
Total 27
0 3 4
0
6
3
0
3 4 0
3 1
0 0 0
1 5 0 2 1
1 0 4 1 4
uncovered cells
intersecting cells

37
Question -18
A factory is going to modify of a plant layout to install four new machines M1, M2, M3 and M4.
There are 5 vacant places J, K, L, M and N available. Because of limited space machine M2 cannot be
placed at L and M3 cannot be placed at J. The cost of locating machine to place in Rupees is shown below:
J K L M N
M1 18 22 30 20 22
M2 24 18 -- 20 18
M3 -- 22 28 22 14
M4 28 16 24 14 16
Required
Determine the optimal assignment schedule in such a manner that the total costs are kept at a minimum.
Solution:
The matrix is unbalanced, we make the matrix balanced by inserting a dummy row and proceed
further.
J K L M N
M1 18 22 30 20 22
M2 24 18 -- 20 18
M3 -- 22 28 22 14
M4 28 16 24 14 16
M5 (Dummy) 0 0 0 0 0
a) Row Reduction
0 4 12 2 4
6 0 -- 2 0
-- 8 14 8 0
14 2 10 0 2
0 0 0 0 0
b) Column Reduction: Not Required

38
Question -19
A car hiring company has one car at each of the five depots A, B C, D and E. A customer in each of the five
towns V, W, X, Y and Z requires a car. The distance in kms, between depots (origin) and the town
(destination) are given in the following table-
Town
Depots
A B C D E
V 3 5 10 15 8
W 4 7 15 18 8
X 8 12 20 20 12
Y 5 5 8 10 6
Z 10 10 15 25 10
Required: Find out as to which car should be assigned to which customer so that the total distance
travelled is a minimum. How much is the total travelled distance?
0 4 12 2 4
6 0 -- 2 0
-- 8 14 8 0
14 2 10 0 2
0 0 0 0 0
Machine Places Cost
M1 J 18
M2 K 18
M3 N 14
M4 M 14
M5 (Dummy) L 0
Total Cost 64
0 4 12 2 4
6 0 -- 2 0
-- 8 14 8 0
14 2 10 0 2
0 0 0 0 0

39
Solution:
The given matrix is a balanced matrix, so we proceed step wise without any improvement to the matrix.
a) Row Reduction
0 2 7 12 5
0 3 11 14 4
0 4 12 12 4
0 0 3 5 1
0 0 5 15 0
b) Column Reduction
0 2 4 7 5
0 3 8 9 4
0 4 9 7 4
0 0 0 0 1
0 0 2 10 0
0 2 4 7 5
0 3 8 9 4
0 4 9 7 4
0 0 0 0 1
0 0 2 10 0
Since the number of lines (=3) is not equal to the order of the matrix (which is 5), the above matrix will not
give the optimal solution. We subtract the minimum uncovered element (=2) from all uncovered elements
and add it to the elements lying on the intersection of two lines. We get the following improved matrix-
0 0 2 5 3
0 1 6 7 2
0 2 7 5 2
2 0 0 0 1
2 0 2 10 0
Again, the minimum number of lines required to cover all the zeros is less than the rows/column, optimal
assignment cannot be made at this stage also. We again improve the matrix.
0 0 0 3 3
0 1 4 5 2
0 2 5 3 2
4 2 0 0 3
2 0 0 8 0

40
Again, the minimum number of lines required to cover all the zeros is less than the rows/column, optimal
assignment cannot be made at this stage also. We again improve the matrix.
1 0 0 3 3
0 0 3 4 1
0 1 4 2
1
5 2 0 0
3
3 0 0 8 0
Question -20
Imagine yourself to be the Executive Director of a 5-Star Hotel which has four banquet halls that can be
used for all functions including weddings. The halls were all about the same size and the facilities in each
hall differed. During a heavy marriage season, 4 parties approached you to reserve a hall for the marriage
to be celebrated on the same day. These marriage parties were told that the first choice among these 4
halls would cost Rs.25,000 for the day.
They were also required to indicate the second, third and fourth preferences and the price that they
would be willing to pay. Marriage party A & D indicated that they won’t be interested in Halls 3 & 4. Other
particulars are given in the following table-
Marriage Party Hall 1 Hall 2 Hall 3 Hall 4
A 25,000 22,500 X X
B 20,000 25,000 20,000 12,500
C 17,500 25,000 15,000 20,000
D 25,000 20,000 X X
Where X indicates that the party does not want that hall.
Required
Decide on an allocation that will maximize the revenue to your hotel.
Customer
at Town
Car at
Depot
Distance
(Km.)
V C 10
W B 7
X A 8
Y D 10
Z E 10
Total 45
1 0 0 3 3
0 0 3 4 1
0 1 4 2 1
5 2 0 0 3
3 0 0 8 0

41
Solution:
We are given a preference matrix stating the amount that the parties are willing to pay for each hall. The
objective of the problem is to maximise the revenue of the hotel. Hence, we are given a revenue matrix.
The cost matrix will be as:
Marriage
Party Hall 1 Hall 2 Hall 3 Hall 4
A 0 2500 X X
B 5000 0 5000 12500
C 7500 0 10000 5000
D 0 5000 X X
a) Row Reduction: Not required [Each row contains at least ONE Zero
b) Column Reduction
0 2500 X X
5000 0 0 7500
7500 0 5000 0
0 5000 X X
0 2500 X X
5000 0 0 7500
7500 0 5000 0
0 5000 X X
The minimum number of lines to cover all zeros is 3 which is less than the order of the square matrix
(i.e.4), the above matrix will not give the optimal solution, and further improvement is required.
The improved matrix will be as:
0 0 X X
7500 0 0 7500
10000 0 5000 0
0 2500 X X
A maximization matrix is to be converted in to the
minimization matrix:
b) Deduct all cell costs from the cell element
selected in (a) above and proceed further.
In this case its 2500
 Deduct the minimum cell cost from uncovered cells
Uncovered cell costs are Cell12 & Cell42
with values 2500 & 5000 resp.
 Add the said minimum cell cost to intersecting cells
Intersecting Cells are Cell21 & Cell31
2500 is to be added to both cells.
 Copy the remaining elements in the coming matrix
as it is.
Copy the remaining values as it is in the improved
matrix.

42
0 0 X X
7500 0 0 7500
10000 0 5000 0
0 2500 X X
0 0 X X
7500 0 0 7500
10000 0 5000 0
0 2500 X X
Marriage Party Hall Revenue
A 2 22,500
B 3 20,000
C 4 20,000
D 1 25,000
Total Revenue 87,500

43
Question -21 [Important]
A salesman has to visit five cities. He wishes to start from a particular city, visit each city once and then
return to his starting point. Cost (in ₹000) of travelling from one city to another is given below:
Required
Find out the ‘Least Cost Route’.
Solution:
Based on the requirement of the question the given matrix is a minimisation matrix.
While solving the question remember the additional requirement of the question i.e.
He wishes to start from a particular city, visit each city once and then return to his starting point
a) Row Reduction
- 3 12 18 0
12 - 3 18 0
12 9 - 0 9
24 0 6 - 3
0 6 3 21 -
b) Column Reduction
- 3 9 18 0
12 - 0 18 0
12 9 - 0 9
24 0 3 - 3
0 6 0 21 -
- 3 9 18 0
12 - 0 18 0
12 9 - 0 9
24 0 3 - 3
0 6 0 21 -
P Q R S T
P - 5 14 20 2
Q 17 - 8 23 5
R 23 20 - 11 20
S 35 11 17 - 14
T 2 8 5 23 -

44
P Q R S T
P - 3 9 18 0
Q 12 - 0 18 0
R 12 9 - 0 9
S 24 0 3 - 3
T 0 6 0 21 -
At this stage no doubt we arrive at minimum cost but the additional condition does not get fulfilled.
The above solution is optimum solution with two routes:
I. Starts from P & reaches destination T & finally comes back to P and
II. Starts from Q & reaches R & then reaches to S & Comes back to Q
To solve this problem we have to bring next minimum element in the matrix i.e.3. Now the possible new
assignments are:
P Q R S T
P - 3 9 18 0
Q 12 - 0 18 0
R 12 9 - 0 9
S 24 0 3 - 3
T 0 6 0 21 -
Note:
Next lowest cost is 3 and Cell (P,Q), Cell(S,R) & Cell(S,T) has same cell cost 3. We may allot in any cells
provided that the additional condition gets fulfilled.
On allotting to Cell(S,R) the additional condition does not get fulfilled.
Allotment may be made at Cell(S,T), the overall cost will be same when assignment is made in Cell(P,Q) or
in Cell(S,T).
Final Answer
From To Cost
P Q 5000
Q R 8000
R S 11000
S T 14000
T P 2000
Total Cost 40000

45
Question-22
A salesman has to visit five cities. He wishes to start from a particular city, visit each city once and then
return to his starting point. Cost (in ` '000) of travelling from one city to another is given below-
Required
Find out the least cost route.
Solution:
Based on the requirement of the question the given matrix is a minimisation matrix.
While solving the question remember the additional requirement of the question i.e.
He wishes to start from a particular city, visit each city once and then return to his starting point
a) Row Reduction
Cities P Q R S T
P - 2 8 0 2
Q 2 - 6 0 2
R 4 2 - 4 0
S 0 0 8 - 8
T 0 0 2 6 -
b) Column Reduction
Cities P Q R S T
P - 2 6 0 2
Q 2 - 4 0 2
R 4 2 - 4 0
S 0 0 6 - 8
T 0 0 0 6 -
Cities P Q R S T
P - 2 6 0 2
Q 2 - 4 0 2
R 4 2 - 4 0
S 0 0 6 - 8
T 0 0 0 6 -
P Q R S T
P - 6 12 4 6
Q 6 - 10 4 6
R 12 10 - 12 8
S 4 4 12 - 12
T 6 6 8 12 -
From
To

46
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
Again we draw minimum no. of straight lines to cover maximum zeros.
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
After making allotment in Cell53 and Cell35 there appears tie. We allot in Cell41.
The next lowest cost cell is 2 so we make allotment in cells where cost is 2.
Possible cells are: Cell 31 Cell 15 Cell 25 Cell 23
We make allotment in all cells with cell cost 2.
The routes and their associated costs are as follows:
From To Cost
P S 4000
S Q 4000
Q P 6000
R T 8000
T R 8000
Total Cost 30000
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
uncovered cells
intersecting cells
The least cost comes to 30000 but this solution does not
fulfil the additional condition of the question ie.
Travelling pattern.
So we shall proceed further to find the alternative route.
The next lowest cost cell is 2 so we make allotment in cells
where cost is 2.
Possible cells are: Cell 31 Cell 15 Cell 25 Cell 23

47
We make allotment in all cells with cell cost 2.
Case I: Allotment made in Cell 15 Case II Allotment made in Cell 31
Cost Sheet: Cost Sheet:
Case III: Allotment made in Cell 25 Case IV: Allotment made in Cell 23
Cost Sheet: Cost Sheet:
Hence, case I fulfils both the conditions, the travelling route is selected as per case I.
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
From To Cost
P S 4000
S Q 4000
Q R 10000
R T 8000
T P 6000
Total 32000
From To Cost
P R 12000
R T 8000
T S 12000
S Q 4000
Q P 6000
Total 42000
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
Cities P Q R S T
P - 0 4 0 2
Q 0 - 2 0 2
R 2 0 - 4 0
S 0 0 6 - 10
T 0 0 0 8 -
From To Cost
P S 4000
S R 12000
R T 8000
T Q 6000
Q P 6000
Total 36000
From To Cost
P S 4000
S T 12000
T R 8000
R Q 10000
Q P 6000
Total 40000

48
Question -23
The cost matrix giving selling costs per unit of a product by salesman A, B, C and D in regions R1, R2, R3
and R4 is given below:
A B C D
R1 4 12 16 8
R2 20 28 32 24
R3 36 44 48 40
R4 52 60 64 56
Required:
(i) Assign one salesman to one region to minimise the selling cost.
(ii) If the selling price of the product is ₹200 per unit and variable cost excluding the selling cost given in
the table is ₹100 per unit, find the assignment that would maximise the contribution.
(iii) What other conclusion can you make from the above?
Solution:
Answer to Point (i)
a) Row Reduction b) Column Reduction
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 8 12 4
0 8 12 4
0 8 12 4
0 8 12 4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
Region
Sales
Person
Selling
Cost
R1 A 4
R2 B 28
R3 C 48
R4 D 56
Total 136

49
Answer to Point (ii)
Particulars Amount
Sales 200
Less: Variable cost before Selling Cost 100
Contribution before Selling Cost 100
Forming contribution matrix: After Including Selling Costs.
96 88 84 92
80 72 68 76
64 56 52 60
48 40 36 44
Since, the matrix is a maximisation matrix we will convert the matrix into a loss matrix.
0 8 12 4
16 24 28 20
32 40 44 36
48 56 60 52
a) Row Reduction
0 8 12 4
0 8 12 4
0 8 12 4
0 8 12 4
This matrix is the same matrix that we have derived in point no. (1) In Step I
So, final answer shall be:
Answer to Point (iii)
i) If a constant is added/multiplied/divided/ subtracted to every element of the matrix in an
assignment problem then an assignment which minimises the total cost for the new matrix will also
minimize the total cost matrix. (i.e. there will be no impact in final solution)
ii) Minimising cost is the same as maximizing contribution.
iii) Many zero’s represent many feasible least cost assignment. Here, all zeros mean maximum
permutation of a 4 X 4 matrix, viz. 24 solutions (4 X 3 X 2 X1) are possible.
Region Sales Person Contribution
R1 A 96
R2 B 72
R3 C 52
R4 D 44
Total 264

50
Question - 24
R3C2 denotes the element at the intersection of the third row and 2nd column. Under this notation, R1C1,
R2C1, R3C1, R3C2, R3C3, R4C3, R4C4, were the only zero elements in a 4x4 minimization assignment
problem after the row minimum and column minimum operations.
(i) In the next step to draw lines to cover zeroes, a student drew 4 horizontal lines covering rows R1, R2,
R3, and R4. Will he arrive at the optimal assignment at the next step? Why? Explain the concept.
(ii) Independent of (i), if you are given the additional information that R2C2 element is lesser than the Row
1 and Row 2 non-zero values, how will you arrive at the optimal solution?
Solution:
Answer to point no. (i)
Framing a 4 X 4 matrix based on the information given. The matrix obtained is a matrix after Row & Column
Operation.
This means Step I (as per our steps) has been completed and Step II is to be started.
C1 C2 C3 C4
R1 0
R2 0
R3 0 0 0
R4 0 0
Now, let’s continue to Step II:
The step performed by the student is as follows: Actually to be done: Correct Solution
C1 C2 C3 C4
R1 0
R2 0
R3 0 0 0
R4 0 0
Assignment is made in the cell which has zero (0) element and other zero elements in the corresponding
row and column is crossed i.e. no further assignment is possible in that row and column in which first
assignment has already been made.
Analysis of the operation performed by the student-
i) The first (assuming) assignment has been made in cell R1C1, leaving no further scope for assignment
in R1 and C1. However, in the above matrix a further assignment has also been made in R2C1, which
could have not been done. It makes the above solution invalid and it will not arrive at the optimal
assignment.
ii) However, assignment in R3C2 or R3C3 and R4C3 or R4C4 is possible provided no other assignment is
made in the corresponding row and column.
C1 C2 C3 C4
R1 0
R2 0
R3 0 0 0
R4 0 0

51
Answer to point no. (ii)
Let us assume that the non-zero values in Row 1 and Row 2 except value at R2C2 is “x" and no assignments
are possible in cells R4C1, R4C2 and R3C4. The following assignment matrix could be as below:
We draw minimum no. of straight lines to cover
maximum zeros.
The optimal assignment will be at R1C1, R2C2, R3C3 and R4C4.
C1 C2 C3 C4
R1 0 N N N
R2 0 (N-1) N N
R3 0 0 0
R4 0 0
C1 C2 C3 C4
R1 0 1 1 1
R2 0 0 1 1
R3 N-1 0 0
R4 0 0
C1 C2 C3 C4
R1 0 1 1 1
R2 0 0 1 1
R3 N-1 0 0
R4 0 0
C1 C2 C3 C4
R1 0 1 1 1
R2 0 0 1 1
R3 N-1 0 0
R4 0 0
Here it is (N-1)
uncovered cells
Uncovered Cells are those cells which
are not touched by even a single line.
intersecting cells
Intersecting Cells are R3C1 & R4C1
Cells touched by single line are to be
incorporated in same form.

52
Question - 25
A BPO company is taking bids for 4 routes in the city to ply pick-up and drop cabs. Four companies have
made bids as detailed below-
Co./Routes R1 R2 R3 R4
C1 4,000 5,000 − −
C2 − 4,000 − 4,000
C3 3,000 − 2,000 −
C4 − − 4,000 5,000
Each bidder can be assigned only one route. Determine the minimum cost that the BPO should incur.
Solution:
For simplicity in calculation we divide all the figures by 1000 and proceed further
1 1 − −
− 0 − 0
0 − 0 −
− − 2 1
0 0 − −
− 0 − 0
0 − 0 −
− − 1 0
0 0 − −
− 0 − 0
0 − 0 −
− − 1 0
Company Route Cost
C1 R1 4,000
C2 R2 4,000
C3 R3 2,000
C4 R4 5,000
Total 15,000
0 0 − −
− 0 − 0
0 − 0 −
− − 1 0

53
Question - 25
A manager was asked to assign tasks to operators (one task per operator only) so as to minimize the time
taken. He was given the matrix showing the hours taken by the operators for the tasks.
First, he performed the row minimum operation. Secondly, he did the column minimum operation. Then,
he realized that there were 4 tasks and 5 operators. At the third step he introduced the dummy row and
continued with his fourth step of drawing lines to cover zeros. He drew 2 vertical lines (under operator
III and operator IV) and two horizontal lines (aside task T4 and dummy task T5). At step 5, he performed
the necessary operation with the uncovered element, since the number of lines was less than the order of
the matrix. After this, his matrix appeared as follows:
Tasks I II III IV V
T1 4 2 5 0 0
T2 6 3 3 0 3
T3 4 0 0 0 1
T4 0 0 5 3 0
T5 (Dummy) 0 0 3 3 0
Required
(i) What was the matrix after step II? Based on such matrix, ascertain (ii) and (iii) given below.
(ii) What was the most difficult task for operators I, II and V?
(iii) Who was the most efficient operators?
(iv) If you are not told anything about the manager’s errors, which operator would be denied any task?
Why?
Solution:
Answer to Point (i)
Let us visualise what the manager did while solving this problem:
Tasks I II III IV V
T1 4 2 5 0 0
T2 6 3 3 0 3
T3 4 0 0 0 1
T4 0 0 5 3 0
T5 (Dummy) 0 0 3 3 0
At the end he improved the matrix with lowest uncovered cell element.
Going in backward way:
(i) The lowest uncovered cell is added to intersection point.
(ii) Cell elements of Dummy row/column are always Zero
(iii) Whenever any element is added to Zero the resulting figure
will be the same element.
(iv)Similarly, Cell 53 & Cell 54 are cell elements of Dummy row
and after improvement they became 3.
This proves that the minimum uncovered cell cost is 3
uncovered cells
intersecting cells

54
Now the previous matrix is as follows
(This is obtained by Deducting 3 from intersecting points and adding 3 to uncovered cell costs and leaving
remaining elements as it is)
Tasks I II III IV V
T1 7 5 5 0 3
T2 9 6 3 0 6
T3 7 3 0 0 4
T4 0 0 2 0 0
Answer to Point (ii)
Based on the Matrix after Step II most difficult task for operator I, II and V are as follows-
Operator I = T2 (9 hours)
Operator II = T2 (6 hours)
Operator V = T2 (6 hours)
Answer to Point (iii)
Based on the Matrix after Step II the most efficient operator is Operator IV.
Answer to Point (iv)
If the Manager’s error is not known, then assignment would be-
Tasks I II III IV V
T1 4 2 5 0 0
T2 6 3 3 0 3
T3 4 0 0 0 1
T4 0 0 5 3 0
T5 (Dummy) 0 0 3 3 0
We continue the assignment; T1 – V, T2 – IV, T3 – III are fixed. Between T4 and T5, I or II can be allotted.
So, operator I or II can be denied the job.

55
Question - 26
Four operators O1, O2, O3 and O4 are available to a manager who has to get four jobs J1, J2, J3 and J4
done by assigning one job to each operator. Given the times needed by different operators for different
jobs in the matrix below-
J1 J2 J3 J4
O1 12 10 10 8
O2 14 12 15 11
O3 6 10 16 4
O4 8 10 9 7
Required
(i) How should the manager assign the jobs so that the total time needed for all four jobs is minimum?
(ii) If job J2 is not to be assigned to operator O2 what should be the assignment and how much additional
total time will be required?
Solution:
Answer to point (i)
This is an assignment problem whose objective is to assign one job to one operator, so that total time
needed for all four jobs is minimum. To determine appropriate assignment of jobs and operators, let us
apply the assignment algorithm.
a) Row Reduction
4 2 2 0
3 1 4 0
2 6 12 0
1 3 2 0
b) Column Reduction
3 1 0 0
2 0 2 0
2 5 10
0
0 2 0 0
3 1 0 0
2 0 2 0
2 5 10 0
0 2 0 0

56
The minimum number of lines drawn to cover all zeros is equal to 4. Since the number of lines drawn viz.,
4 is equal to the number of jobs or the number of operators, so we proceed for making the optimal
assignment.
Answer to point (ii)
If job J2 is not to be assigned to operator O2 then this objective can be achieved by replacing the time for
cell (O2, J2) by a very large time estimate say M (Alternatively we may leave that cell blank and proceed
further).
Now apply the assignment algorithm to the following matrix so obtained-
12 10 10 8
14 M 15 11
6 10 16 4
8 10 9 7
4 2 2 0
3 M 4 0
2 6 12 0
1 3 2 0
Since the minimum number of lines drawn in the above matrix to cover all the zeroes is 3 which is less
than the number of operators or jobs, therefore the above table will not yield the optimal assignment. For
obtaining the optimal assignment we increase the number of zeros by subtracting the minimum
uncovered element from all uncovered elements and adding it to elements lying at the intersection of two
lines, we get the following matrix-
3 1 0 0
2 0 2 0
2 5 10 0
0 2 0 0
Operator Job Time
O1 J3 10
O2 J2 12
O3 J4 4
O4 J1 8
Total Time 34
3 0 0 0
2 M 2 0
1 4 10 0
0 1 0 0
3 0 0 0
2 M 2 0
1 4 10 0
0 1 0 0

57
3 0 0 0
1 M 1 0
0 3 9 0
0 1 0 0
Additional total time required will be 2 (36 – 34) units of time.
Operator Job Time
O1 J2 10
O2 J4 11
O3 J1 6
O4 J3 9
Time 36
3 0 0 0
1 M 1 0
0 3 9 0
0 1 0 0

Assignment Chapter - Q & A Compilation by Niraj Thapa

Empfohlen

Empfohlen

Weitere ähnliche Inhalte

Was ist angesagt?

Was ist angesagt? (20)

Andere mochten auch

Andere mochten auch (17)

Ähnlich wie Assignment Chapter - Q & A Compilation by Niraj Thapa

Ähnlich wie Assignment Chapter - Q & A Compilation by Niraj Thapa (20)

Mehr von CA Niraj Thapa

Mehr von CA Niraj Thapa (9)

Kürzlich hochgeladen

Kürzlich hochgeladen (20)

Assignment Chapter - Q & A Compilation by Niraj Thapa